Гидроманипуляторы в подводной и радиационных средах: обзор тенденций

Благодарности. Работа выполнена в рамках Государственного задания на 2022 год № 075–01623– 22–01 «Поиск путей создания глубоководного гидравлического манипулятора для подводнотехнических работ, в том числе в условиях ионизирующего излучения» (FNRG-2022–0021, регистрационный номер 1021101316133–1–2.2.2).

Цитирование: Копылов В. М. Гидроманипуляторы в подводной и радиационных средах: обзор тенденций / В. М. Копылов, В. В. Титов, А. А. Трутс. Журн. Сиб. федер. ун-та. Техника и технологии, 2023, 16(3). С. 316–340. EDN: QWPWYI менение ферритных нержавеющих сталей) и электропроводностью самой жидкости (необходима дополнительная изоляция). Положительным влиянием жидкой среды является (в случае ее низкой температуры) улучшенный теплообмен, что может повысить максимальный продолжительный момент привода. Для работы электропривода в радиационных полях и в жидких средах необходимо обеспечить изоляцию и герметизацию, а также другие меры для живучести изделия. Отдельным вопросом стоит размещение датчиков положения ротора, который является неотъемлемой частью электропривода с хорошими характеристиками.

Альтернативой электроприводу, часто применяемой в экстремальных средах и там, где нужны большие усилия при умеренных скоростях движения, является гидропривод. Основным достоинством гидропривода является большой удельный момент и мощность. Массовый удельный момент у среднего гидропривода может составлять до 100–200 Нм/кг (и массовую удельную мощность свыше 600 Вт/кг) [1]. Данные показатели могут быть увеличены за счет повышения давления в магистрали. В случае больших скоростей и моментов гидравлический привод выигрывает по сравнению с электроприводом [4, с. 80].

Основным недостатком гидропривода является его низкая эффективность. В первую очередь она связана с двойным преобразованием энергии (электрическая–механическая–гидрав-лическая) и потерями в преобразователях. Второй основной источник потерь – это утечки, которые для ряда задач могут быть практически полностью убраны [5]. Потери на трение в гидросистеме также неизбежны [6, 8]. Их можно снижать, но в конечном счете они являются основными в гидравлических системах. По данным разных авторов, КПД гидропривода составляет 30–40 %, в то время как у электропривода до 80 % (в номинальных режимах). Кроме того, гидропривод имеет существенно нелинейную динамику, что требует сложных систем управления и специальных мер по снижению негативных эффектов, вызываемых нелинейностями (как программных, так и аппаратных).

В подводной робототехнике доминируют именно гидравлические манипуляторы, особенно применительно к телеуправляемым системам. В части автономных систем с независимым питанием высокое потребление с низким КПД делает гидропривод менее предпочтительным по сравнению с электроприводом [4]. К 2000 г. очень мало подводных аппаратов было оснащено манипуляционными системами [7]. Приблизительно с 2010 г. начали появляться подводные манипуляторы с электроприводом (например, SAUVIM [9,10]). Кроме того, компоненты гидропривода обладают высокой стойкостью к воздействию радиации, что делает их особенно привлекательными в атомной индустрии.

Основные факторы, влияющие на манипулятор в водной среде, – коррозия и давление. Высокое давление требует создания герметичных кожухов, защищающих аппаратуру от коррозии и короткого замыкания. Чем выше перепад давление внутри и снаружи, тем более больше должны быть уплотнения в подвижных и неподвижных соединениях. Снизить требования к уплотнениям возможно двумя путями: компенсацией перепада давления и заполнением внутреннего объема изолирующей жидкостью.

Другой проблемой является коррозия, которая снижает механические свойства несущих конструкций и увеличивает трение в сочленениях. Борьба с коррозией осуществляется приме-– 318 – нением коррозионно-стойких материалов и смазок. В иностранных источниках можно встретить следующие наиболее распространенные материалы для звеньев манипулятора [11]: титан (Ti 6–4), анодированные алюминиевые сплавы (5083, 6082 T6, 6061 T6, 7075 T6, A356), нержавеющие стали (316, 630, 660), некоторые пластики (полиэтилен).

Примерно до 2010 г. доминантным типом привода для подводных манипуляторов был гидравлический. Манипуляторы на основе гидропривода имеют отношение собственного веса к поднимаемой нагрузке до 3, тогда как для манипуляторов на электроприводе это соотношение не более 1 (для коммерчески выпускаемых). Так как гидравлика работает на жидкости (под давлением), такие манипуляторы частично защищены от попадания внутрь жидкости, в которую они погружены. Управление движением осуществляется регулированием потока через дроссели. Дроссели могут располагаться непосредственно вблизи гидроактуатора (в этом случае необходимо принимать специальные меры по обеспечению гидроизоляции последней), в отдельном гидроизолированном объеме, и быть интегрированными в актуатор [5].

Ведущими производителями подводных манипуляторов являются Kraft Telerobotics, Schilling Robotics, Cybernetix, Hydrolek. Среди гидравлических манипуляторов для радиационного применения следует выделить Brokk.

Манипуляторы с электроприводом начали применяться в подводной робототехнике сравнительно недавно. Основная проблема электропривода (помимо низкого соотношения массы манипулятора к массе поднимаемого грузка) – это необходимость в гидроизоляции, которая достигается масляным заполнением внутреннего объема, использованием прямого привода и коррозионно-стойких магнитомягких сталей (в последнем случае допускается прямой контакт внутреннего объема двигателя с окружающей средой, но это ведет к постепенному накоплению твердых включений и осадков внутри двигателя и выходу последнего из строя). Прямой привод обеспечивает низкий момент и высокую скорость, что не является предпочтительным в манипуляционных системах. Экспериментальные методы герметизации, такие как магнитные муфты, не нашил широкого применения в индустрии, т.к. передаваемый ими момент ограничен и связан с массо-габаритными размерами муфты. [12, 13]. Основным преимуществом электродвигателя является точность отработки траектории и умеренная нелинейность динамики [14].

В [15,16] представлен обзор применения робототехники в атомной индустрии и выделены основные задачи, требующие автоматизации:

– проверка и инспекция;

– вывод из эксплуатации, разборка, демонтаж, т.д.;

– ремонтные работы;

– сортировка радиоактивных отходов;

– обслуживание и сопроводительные работы;

– ликвидация последствий аварий.

Все существующие системы с телеуправлением можно разделить на три категории: сравнительно дорогие решения под конкретную узкоспециализированную задачу; решения на основе стандартного оборудования, адаптированные под конкретную задачу; использование го-– 319 – товых компонент (например, гидроманипуляторов) без существенной доработки (обычно для простых задач, с расчетом на полную или частичную замену или ремонт сразу после или в процессе эксплуатации). Гидроманипуляторы используются в основном в задачах вывода из эксплуатации, разборки, транспортировки и сортировки отходов (пример в [17,18]).

Как и в других индустриях, операции, в задачах представленных выше, можно разделить на: требующие высокой точности и сложности исполнения и повторяющие рутинные операции низкой сложности (но, возможно, высокой точности) [15]. Часто выполняемые операции по обслуживанию и ремонту объектов атомной инфраструктуры должны быть оптимизированы по скорости, точности и дешевизне выполнения.

Опыт применения роботов для ликвидации последствий аварий (Фукусима в 2011 г. и на Чернобыльской АЭС в 1986 г.) показал высокие требования по надежности (отсутствие сбоев) и устойчивости к сбоям (восстановление после сбоя). Основной поражающий фактор (радиация) действует по-разному на разные части манипуляционной системы. В [19] приводятся ориентировочные характеристики излучения в различных участках атомной электростанции (АЭС) и при различных операциях. Данные показывают порядок величин по мощностным характеристикам излучения. Здесь приводится краткая выжимка относительно наиболее интересных с точки зрения применения манипуляторов участков АЭС (табл. 1).

Таблица 1. Сводные данные по радиационным нагрузкам на АЭС (во время сервисного обслуживания)

Table 1. Dose rates at a nuclear plant (reference values during maintenance)

Участок	Гамма, Гр/ч	Нейтроны, Гр/ч
По внешней поверхности реактора	100	300
Вблизи первого контура охлаждения	0,5	мало
Вблизи парогенератора	0,15	мало
В бассейне выдержки (вблизи топлива)	103–104	мало
Внутри машины с топливными элементами	105	102
Разрезание топливных элементов	103
Остекление отходов	До 104	4*10–4
Высокоактивные остекленные отходы	1,8*103	2*102
Среднеактивные отходы	6	0,45

Радиационные эффекты в материалах, применяемых в гидравлических и пневматических приводах

Можно выделить четыре основные группы материалов, работающих в гидроприводе: материалы корпуса, магистрали, уплотнения и рабочая жидкость. Рабочий газ в пневматических системах не испытывает долговременных радиационных изменений, но обычно ионизуется. При использовании воздуха или других смесей, содержащих кислород, этот процесс может приводить к образованию озона, что вызывает ускоренную химическую коррозию уплотнений и магистралей и в меньшей степени корпусов. Однако в большинстве случаев применения пневматики в радиационно-опасных средах в качестве рабочего тела используются инертные – 320 – газы, ионизация которых не приводит к негативным эффектам. В качестве материалов корпусов обычно используются металлы, преимущественно – нержавеющая сталь. Применение коррозионно-стойких сталей обусловлено требованием возможности дезактивации, которая производится омыванием растворами кислот (щавелевой, уксусной), ПАВ и щелочей. Длительное облучение хромоникелевых сталей приводит к диффузии легирующих элементов к поверхности сталей, в то время как сердцевина материала становится обедненной [20], что приводит к снижению прочности материалов. Характерные поглощенные дозы, при которых проявляется данный эффект, оцениваются величиной 0,5 МГр.

Уплотнения, а также магистрали зачастую изготавливаются из эластомеров и термореактивных смол, а также фторопластов. Последние обладают рядом привлекательных свойств для уплотнений, такими как химическая инертность, низкий коэффициент трения и смазывающие свойства, что значительно снижает потери при работе. Однако испытаниями на радиационную стойкость [21] установлено, что из всех пластиков фоторопласты обладают одним из наименьших значений допустимой поглощенной дозы, не превышающей 2 кГр. Превышение этого значения ведет к деградации поверхностных слоев, появлению микротрещин, а при величине поглощенной дозы более 5 кГр материал, как правило, разрушается, если работает в условиях динамических нагрузок. Полиэтилен и полипропилен обладают гораздо большей стойкостью [21], особенно марки, полученные при высоком давлении, и обеспечивают нормальную работу при поглощенных дозах до 100 кГр. Наилучшие показатели стойкости демонстрируют силиконы и другие кремнийорганические соединения, а также ПЭТФ, работающие при суммарных дозах до 1 МГр. Все эластомеры обладают низкой радиационной стойкостью, обычно менее 10 кГр, а увеличение утечек через эластомерные уплотнения по газу наблюдается уже при дозах в 1–2 кГр [22]. В качестве замены эластомерным уплотнениям может быть предложен терморасширенный графит, чья стойкость к радиации огромна (более 1 ГГр), однако прокладки из этого материала не являются в полной мере герметичными [23] (ТУ 5728–006–93978201– 2008), особенно при работе в пневматических системах.

Магистрали гидравлических систем часто находятся в наиболее жестких условиях по облучению, по сравнению с другими компонентами, поскольку обычно применяется внешняя укладка трубопроводов. В настоящее время именно магистрали ограничивают радиационную стойкость гидравлических манипуляторов, поскольку снижение относительного удлинения и рост твердости являются наиболее выраженными эффектами радиационного старения, и именно эти эффекты усиливаются при нормальной эксплуатации шарнира, вокруг которого проложена гибкая магистраль. Несмотря на более тяжелые условия эксплуатации, применение распределительных шайб (подвижных сочленений гидролиний) с уплотнениями из термореактивных материалов в сочетании с металлическими жесткими магистралями обеспечивает лучшие показатели надежности при высоких значениях поглощенных доз, чем применение гибких магистралей.

Радиационные эффекты в гидравлических жидкостях сводятся к радиационному сшиванию органических компонент жидкости, что приводит к выпадению осадка, способного забивать фильтры и мешать работе скользящих уплотнений. В данной области хорошие результаты по стойкости демонстрируют сверхвысоковакуумные масла на основе силоксанов [3], обеспечивающие стойкость до 18 МГр. Однако сравнительно высокие значения вязкости и напряже-– 321 – ний поверхностного натяжения таких жидкостей означают более высокие потери на трение, особенно в узких каналах.

Математические модели элементов гидропривода

В число элементов гидропривода входят:

• –    источники гидравлической энергии;

• –    элементы управления (дроссели, сенсоры);

• –    актуаторы (гидроцилиндры, гидромоторы);

• –    прочие элементы (аккумуляторы, соединительные гидролинии, вторичные измерительные устройства, предохранительные клапаны, системы охлаждения т.п.).

Источниками гидравлической энергии, как правило, служат гидронасосы, вращаемые, в свою очередь, электродвигателем или двигателем внутреннего сгорания (ДВС). Для мобильных гидравлических систем предпочтительным является ДВС из-за большей емкости энергоносителя и возможности его оперативной замены. В мобильных система встречаются также электропривод насосов (в случае мобильной робототехники).

В стационарных системах, где используется регулируемый насос, чаще применяют электропривод, благодаря удобству управления. В качестве привода насоса используются синхронные и асинхронные электродвигатели. В зависимости от способа управления насосом необходимо использовать различные модели последних. Чаще всего управление гидронасосом осуществляется за счет наклона шайбы, регулирующей рабочий объем. Двигатель в этом случае находится в режиме поддержания постоянной скорости (или постоянной мощности, в зависимости от способа управления). Можно считать, что двигатель находится в установившемся режиме. Электродвигатель в этом режиме может быть приближен моделью двигателя постоянного тока (1)-(3) [24]

\=r_ai_a+L_a^ + o>_ek_r , С ¹ )

TAW. • (2)

T,=J'-to,+BV₍»,+T_L (3) (индекс указывает на то, что величина измеряется в физических, а не электрических градусах), где va – напряжение на щёточном контакте, ra – сопротивление обмоток, ia – ток в обмотках, kv – постоянная противо-ЭДС (В*с/рад), ωrkv – величина противо-ЭДС, La – индуктивность обмоток, Te - электромагнитный момент, roe - скорость ротора, km -постоянная момента, J' -приведенная индуктивность нагрузки, TL –приведенный внешний момент, – коэффициент вязкого трения.

В случае если двигатель работает не в постоянном режиме, а изменяет обороты в зависимости от потребностей гидросистемы, должна применяться более точная модель, соответствующая конкретному типу двигателя.

Наиболее распространенным элементом управления гидроприводом (в основном в системах, где один гидронасос работает на несколько гидроприводов) является дроссель, который регулирует направление давления (и потока) в магистрали и сопротивление течению жидкости.

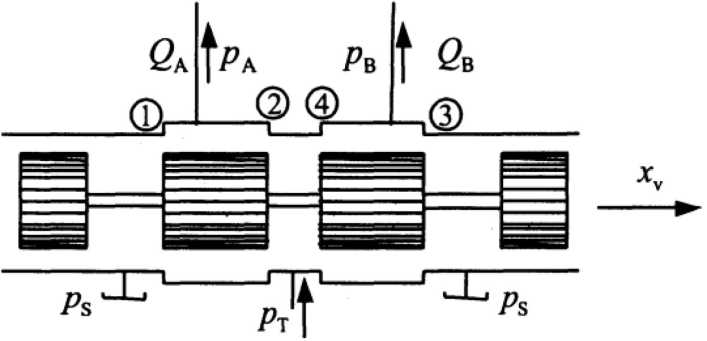
Рис. 1. Одноступенчатый дроссель [25]

Fig. 1. Single-stage throttle [25]

Различают дроссели с пилотным управлением (регулируемым зазором) и дискретные (двух-или трехпозиционные, меняющие направление потока, но имеющие фиксированное раскрытие и гидравлическое сопротивление). Также различают одноступенчатые и многоступенчатые дроссели. Многоступенчатые дроссели применяются в системах с большим давлением и расходом, где требуются большие усилия для перемещения золотника дросселя (эффекты залипания под действием давления в магистралях и пр.). Смещением золотника основного дросселя управляет дроссель меньшего размера, питающийся от той же гидролинии.

Модель одноступенчатого дросселя (рис. 1) можно описать следующими зависимостями (4)-(5) [25]

Qa = ^cvi • <^ + Ч)' ^sig”(P_s -PaY 4\P_s-Pa\

- ^cn • ^„2 + 4) • siMPa - Pt ) • 4\Pa"Pt I,                        (4)

Qb = ^cv3 • ^sg(^xu3 ^+xvY signup, -p_By J\p_s-p_B I

,                                     (5)

где QA, QB — расходы на выходах из дросселя, p_A, p_B - давления на выходе из дросселя, p_s - давление гидролинии высокого давления, pT – давление гидролинии низкого давления, xv – смещение золотника из среднего положения, x_u1.₄ - величины перекрытий/зазоров в среднем положении золотника, sg – функция вида (6)

fx,x>0

^№|o,.v₅o ■                                       ⁽⁶⁾

Динамика работы одноступенчатого дросселя может быть в первом приближении описана системой второго порядка (7)

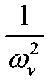
XV 4--L

Ч

x>x;+f_hs-sign(x'?) = K_Y -У ,

где ω v – собственная частота системы, D v – коэффициент затухания, f hs – коэффициент при компоненте, учитывающей гистерезис в работе золотника (залипание на сухом трении), K v – коэффициент перевода силы, – нормализованное по диапазону перемещений смещение золотника.

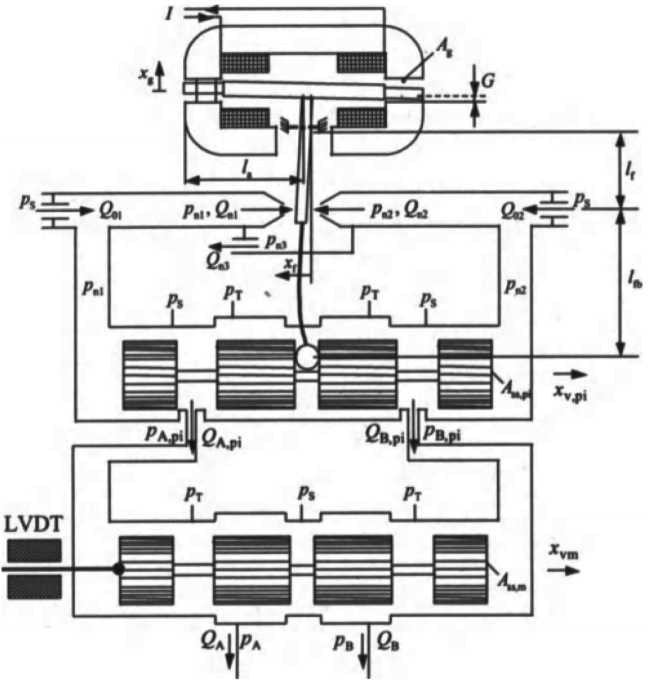
Рис. 2. Трехступенчатый дроссель [25]

Fig. 2. Three-stagethrottle [25]

Данная модель позволяет учесть основные особенности золотниковых дросселей: наличие мертвой зоны (при наличии перекрытия в среднем положении), зависимость потока от корня из перепада давления (или квадратичная зависимость перепада давления от потока), залипание на сухом трении (гистерезис). В данной модели не учитываются силы, действующие на золотник в силу перепадов давления между магистральной линией и потоком на поверхности золотника.

Пример многоступенчатого золотникового дросселя представлен на рис. 2. Работа данного дросселя основана на управлении положением главного золотника x vm (нижний) через давления p n 1 , p n ₂, регулируемые положением управляющего дросселя x_v , pi (средний). Положение управляющего (пилотного) дросселя, в свою очередь, задается через балансировку потоков Q n 1 , Q n ₂ (сопротивлений) двух дросселей типа сопло-заслонка. Положение заслонки X f определяется положением x_{v, pi} управляющего дросселя и положением соленоида x_g , расположенного в верхнем. Положение главного золотника измеряется индуктивным датчиком линейного положения (LVDT).

Потоки Q A , Q B , Q A, pi , Q B, pi и давления p A , p B , p A, pi , p B, pi связаны зависимостями, аналогичными (4)-(7).Связь между давлениями и потоками сопла-заслонки (8)-(10)

,(8)

,(9)

йп^=Сп<^Рт"Рпз\ ’

Xf0 - среднее положение заслонки, cn 1 , cn₂, cn ₃ - коэффициенты, зависящие от диаметра сопла, коэффициентов сопротивления, т.д.

Положение заслонки xf в статике определяется балансом моментов Ka ∙ xf Ta ⁺ Tfl Tfb, где Ka – упругость заслонки, Ta ≈ β ∙ Is – момент управляющего соленоида ( Is – ток соленоида, β – коэффициент момента соленоида), Tfl – момент от потока, Tf_b – момент обратной связи, получаемой от положения пилотного дросселя (может быть механической или электрической). Приближенно момент от потока можно вычислить (11)

Та = (k_v + k, • x"_f) •

nX ~ Pm) + ^ ' */' (P„i ~ Pm ~ ²' P,x

),                      ⁽¹¹⁾

k 1 , k 2 , k з — коэффициенты, зависящие от геометрии сопла и заслонки.

Представленные уравнения статики для трехступенчатого дросселя дают представления о сложности процессов управления такими дросселями. Уравнения динамики, представленные, например, в [25], могут быть использованы при построении систем управления такими дросселями. Приведенная схема не является единственной. Другие схемы можно найти, например, в [26], где выделяется три основных вида управляемых дросселей: пропорциональные дроссели с контролем направления, пропорциональные дроссели давления и расхода. Последние два обладают внутренней структурой (с механическими и гидравлическими обратными связями), позволяют обеспечивать заданные давление или расход на выходе. В рамках рассмотрения сложных систем (включающих множество дросселей и актуаторов) можно рассматривать упрощенную модель многоступенчатого дросселя, заменяя последний одноступенчатой моделью (4)–(7). Параметры такой модели можно получить экспериментальным путем и они уже не имеют отношения к реальным физическим процессам в системе.

Широко распространенные линейные гидроцилиндры можно описать следующими зависимостями (12), (13)

Ол-Оь-V^fl^-flP, ,                                 (12)

E(PA)

о      о -у —  ,                              (13)

Е(рв)

где QA, QB - расходы камер цилиндра, QLi, Q_Le - внутренние и внешние расходы утечек, VA = VA о - x_p • A_p, VB = VB о - a • x_p • A_p - мгновенные объемы гидроцилиндров (VA ₀, VB ₀ - объемы в нейтральном положении, α – коэффициент, учитывающий уменьшение объема камеры В за счет штока, Ap – площадь штока), xp – положение штока, E (.) – модуль упругости жидкости (в общем случае зависит от давления и температуры, вследствие наличия газов). Несложно получить соответствующие производные V⁷^ = х_р • А_р, V_B = -а • х_р • А_р .

Уравнение движения штока имеет вид (14)

• т, • х_р + F_f (х_р) = (р_А - а • р_в) • А_р - F^ ,                                     (14)

m t = m p + (V A + V B ) • p - кумулятивная масса ( m_p - масса штока), p - плотность жидкости, F f (x_p ) -сила трения (популярными моделями трения являются модель Страйбека и LuGre), F_ext – внешняя сила, действующая на шток.

Цилиндры часто исполняются в форме полудуг для обеспечения криволинейного или вращательного движений.

В робототехнике наибольшее распространение получи роторные поршневые насосы и моторы. В них вращательное движение внешнего привода переводится в поступательное движение группы поршней (или, наоборот, поступательное движение поршней – во вращательное движение выходного вала). Классификацию роторно-поршневых насосов можно найти в [8]. Основное применение нашли аксиально-поршневые насосы и аксиально и радиально поршневые моторы. Аксиально-поршневые насосы выполняются с подвижной шайбой для регулировки подачи. Так как данные машины являются обратимыми, то насосы могут работать как моторы и наоборот.

Уравнения движения роторов гидронасоса (15) и гидромотора (16) практически одинаковы

,                                                     (15)

.'■Ф+т1,)М = т.+—^м ,                                 (16)

1м где J- приведенный к валу момент инерции, ф - угол поворота вала, Tm - момент нагрузки, пР, ηM – КПД насоса и мотора соответственно, TM – момент насоса и мотора.

Расход насоса              зависит от скорости вращения и рабочего объема гидронасоса Vp. Рабочий объем гидронасоса с регулируемой шайбой              зависит от угла наклона шайбы αp и коэффициента Cp, учитывающего геометрические параметры.

Моменты гидронасоса и гидромотора следуют из закона сохранения энергии и выражаются (17)

• V.

  
  

T^^PhL,

A p_HL - перепад давления между линией высокого и низкого давлений, i е { P, M }.

Гидролинии являются неотъемлемым элементом гидросистем. Динамикой гидролинии можно пренебречь, если длина волны колебаний в гидролинии много больше длины самой гидролинии. Более точно это условие выражается формулой (18) [25]

/<----

10-Л где l – длина гидролинии,          – скорость распространения звуковой волны в гидролинии

( p - плотность жидкости, E' - кумулятивный модуль Юнга, учитывающий упругие свойства жидкости с газом, а также упругость стенок. E' в общем случае зависит от давления), f_max - максимальная частота процессов в системе.

Выражение (18) может нарушаться в ряде случаев: источник давления находится далеко от управляющего дросселя, актуатор расположен далеко от дросселя. В этом случае гидролиния представляет собой длинную линию с распределенными параметрами. В операторной форме – 326 – соотношение давления и расхода в начале (Q 1(s), p 1(s)) и конце (Q2(s), p2(s)) гидролинии можно выразить зависимостью (19) [25]

№)

рМ

coshr(s)

-Z_c • 4М$) • sinh Г(5)

• sinh F(s) 2_с-4«№ coshr(s)

p^s)

где s - оператор Лапласа, ZC = р • c / A_pl - характеристическое (волновое) сопротивление гидролинии ( Apl – площадь поперечног о сеч ения гидролинии), – оператор распространения волны, – динамическая функция вязкости (20)

NW-X^^V*-^-*-^- ,              (2°)

s 1+А$ i+A$ 1+А$

р р р где ц - фактор вязкого трения (не путать с коэффициентом вязкого трения), K1..з, в 1..3 — постоянные коэффициенты. Выражение (17) при линейном вязком трении редуцируется до (21)

7V(s) = l + —.                                                              (21)

Таким образом, гидролиния большой длины представляет собой еще один объект в общей системе. Ее динамику часто включают в динамику гидроактуатора для упрощения представления модели.

В гидросистемах часто применяются гидроаккумуляторы, являющиеся накопителями энергии (как правило, в механической форме или в виде давления газа), которую впоследствии можно перевести обратно в гидравлическую. Они являются прямыми аналогами конденсаторов в электротехнике и используются для компенсации быстрых просадок (скачков) давления в системе. Они часто устанавливаются в непосредственной близости от источников давления/ расхода (гидронасосов) или вблизи дросселей, где возможны быстрые изменения давления, способные повлиять на другое оборудование в гидросети (рис. 3).

Уравнение расходов в точке k схемы рис. 3 (22) [27]

Q.u-Q.^Qa,                                        (22)

где О_пк = 4,._к • //„ ,,-, (?„__Lt = 4,__и • и—р. - расходы до и после точки k ( An, k , An, k - площадь просвета гидролинии, u_n, _k , u_{n +1} , _k - скорости потока до и после точки k), Q_A = dV_A ! dt - расход гидроаккку-мулятора ( VA – объем гидроаккумулятора).

Для газового гидроаккумулятора справедлива зависимость (23) между объемом и давлением

,

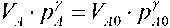
где – объем и давление в гидроаккумуляторе, – объем и давление в гидроаккумуляторе в нейтральном положении (или уставочные значения), γ – адиабатическая постоянная газовой пружины.

Динамика давления в гидроаккумуляторе описывается (24)

= Ba dt у KJ

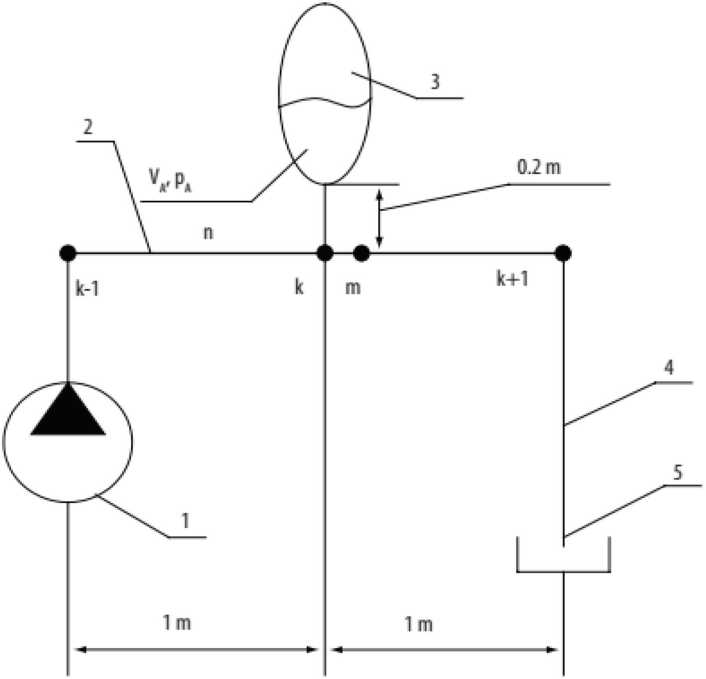
Рис. 3. Гидроаккумулятор в гидросети [27]: 1 – насос, 2 – гидролиния (до точки подключения гидроаккумулятора k), 3 – гидроаккумулятор, 4 – гидролиния (после точки k), 5 – бак

Fig. 3. Hydraulic accumulator in the hydraulic network [27]: 1 – pump, 2 – hydraulic line (up to the point of connection of the accumulator k), 3 – hydraulic accumulator, 4 – hydraulic line (afterthe accumulator k), 5 – tank

Приведенные здесь для справки модели элементов гидропривода не являются исчерпывающими. Многие авторы предлагают более сложные и детализированные модели. Модели других элементов, не приведенных в данном обзоре (например, клапанов и других видов дросселей), также являются существенно нелинейными. К общим замечаниями относительно моделирования гидроэлементов можно отнести:

• –    большинство моделей гидравлики являются разрывными и, как правило, моделируются в гибридном подходе к моделированию [28];

• –    большинство элементов допускает линеаризацию их динамики линейными системами второго порядка;

• –    поведение гидравлической части системы описывается динамикой давления и расхода, что удобно для представления и моделирования в форме системы портов (port-basedsystems) [29].

Модели гидроманипуляторов

Динамика гидравлических манипуляторов описывается так же, как и динамика манипуляторов на других видах приводов и в общем случае может быть представлена через уравнения Лагранжа для неинерциальных систем. Учет гидродинамики осуществляется введением дополнительных обобщенных сил в уравнения Лагранжа, а также введением параллельно модели динамики приводной части (динамика гидропривода), зависящей от обобщенных координат, – 328 – принятых в кинематической модели манипулятора. К динамике подводных манипуляторов добавляется влияние гидродинамических сил жидкости, в которую погружен последний (плавучесть, присоединенная масса, диссипативные силы вязкого трения, подъемные силы/эффект крыла, т.д.), что делает модель динамики еще более сложной и добавляет сложно идентифицируемые величины [11]. Наиболее значимыми оказываются силы вязкого трения (на больших скоростях движения), подъемные силы (эффект крыла) и эффект присоединенной массы (при ускоренном движении в жидкости и разгоне массы окружающей жидкости). Влияние плавучести на динамику неоднозначно, т.к. ее часто используют для компенсации действия силы тяжести.

Системы управления должны быть построены таким образом, чтобы справляться с сильно нелинейной и частично неизвестной и нестационарной динамикой манипулятора и среды. Большинство работ по управлению подводными манипуляторами носит теоретический характер сапробацией через симуляцию. В [30] приводится нелинейная модель подводного манипулятора и адаптивное управления с эталонной моделью. Динамика манипулятора учитывает гидродинамические эффекты на основе уравнения Моррисона. Авторы приходят к выводу, что кориолисовы силы пренебрежимо малы в сравнении с гидродинамическими, а доминирующими являются массовые инерциальные силы и инерциальные силы присоединенной массы воды.

Каждое звено манипулятора испытывает на себе гидродинамические силы (присоединенная масса, плавучесть, сила вязкого трения в жидкости, т.д.). По версии [4, 614], на малых скоростях основной силой является сила вязкого сопротивления среды, воздействие которой на бесконечно малый участок поверхности i-го звена можно найти как (25) (и для целого звена как (26))

, (25)

D, =7/^^|6/Ч,ф’,,И, (26) о где CD – коэффициент вязкого трения, ρ – плотность жидкости, bidx – проекция площади элементарного элемента поверхности на нормаль к скорости, vri – скорость элемента поверхности относительно потока.

Общее движение манипулятора в отсутствие течения жидкости представляется в форме (для последовательных манипуляторов) (27), (28)

М^>^С_т^Л^П_т^Л^Р_т(^О_т^т_а = T_m(q,q,P) ,       ⁽²⁷⁾

Р^КРЛЛ")

где      – обобщенные координаты манипулятора,        – вектор моментов/сил приводов,

– матрица масс (включающая присоединенную массу),             – вектор кориолисовых и центробежных сил/моментов,            – вектор гидродинамических сил,

– трение в шарнирах и приводах манипулятора,       – вектор дополнительных моментов от неучтенных динамических процессов и внешних воздействий,         – нели нейная модель динамики системы гидроприводов, p – вектор давлений в системе приводов, n – число сочленений манипулятора.

Особенностью систем (27), (28) является разность между скоростью протекания процессов в модели системы твердых тел и части модели гидравлики. Система оказывается с двумя масштабами времени (Тихоновские системы). Пример реализации численного моделирования таких систем представлен в работах [31,32], где используется модифицированный метод Ньютона-Рафсона, а также рассматривается факторизация задачи в форме системы портов (port-basedsystems).

Управление движением

Управление гидравлическими манипуляторами преследует две основные цели [33]: улучшение динамических характеристик и борьба с колебательными процессами, присущими гидравлическим системам. Два основных пути улучшения динамических характеристик можно найти в литературе: улучшение динамических свойств гидравлических элементов (аппаратно) и применение различных методов управления. Увеличение быстродействия гидравлических элементов достигается различными способами:

• –    снижением гидравлического сопротивления (за счет правильного дизайна самого элемента);

• –    снижением массо-инерционных свойств элемента;

• –    применением в параллельном включении нескольких элементов с меньшей пропускной способностью, но большим быстродействием [34].

В работе [34] рассматривается увеличение быстродействия дросселя, в то время как быстродействие системы много меньше быстродействия дросселя. Однако быстродействие насоса, как правило, сопоставимо с (требуемым) быстродействием системы, чем вызвано ограничение характеристик последней. Данную проблему решали несколько авторов (например, [35, 36]) в основном в контексте управления насосом.

Улучшение динамики через управление связано с существенной нелинейностью объекта управления, как гидравлического механизма, так и механизма, помещенного в жидкую среду.

Манипуляторы в подводной среде, как и обычные манипуляторы, представляют собой многотельную динамическую систему. Из теории [37] известны две группы подходов к управлению: централизованная и децентрализованная.

В первом случае взаимовлияние степеней свободы системы учитывается в динамической модели и законах управления. Во втором все степени свободы считаются независимыми, а взаимовлияние рассматривается как внешнее возмущающее воздействие.

В гидравлических системах дополнительные нелинейности возникают при ламинарном и турбулентном течении жидкостей в магистралях манипулятора и в потоках жидкости вокруг нее. Кроме того, влияние температуры на вязкость жидкости необходимо учитывать в ряде случаев [38].

Децентрализованные схемы управления

Базовые алгоритмы управления на основе ПИД-регуляторов имеют низкую точность в динамике, которая меняется при изменении конфигурации манипулятора [53],[17]. В [19] на основе проведенных модельных и физических экспериментов на подводном гидравлическом – 330 – манипуляторе констатируется необходимость наличия самонастройки и адаптации в законах управления, реализованных в [56]. Работа [57] описывает использование нечеткой логики в настройке коэффициентов ПИД-регулятора. В [38] описывается применение адаптивного алгоритма с эталонной моделью с коррекцией параметров в реальном времени.

Относительно большое количество работ, посвященных различным формам адаптивных алгоритмов управления для гидравлических манипуляторов, показывает улучшение переходных процессов относительно регуляторов с фиксированными параметрами, но больше внимания получили централизованные алгоритмы, компенсирующие влияние взаимосвязей степеней свободы напрямую.

Централизованные схемы управления

Централизованные схемы управления опираются на знание динамики манипулятора и компенсируют взаимосвязи и нелинейные эффекты, вместо того чтобы пытаться уменьшить их влияние на траекторию движения [37, 4].

В работе [30] рассматривается управление подводным гидравлическим манипулятором. Авторы применяют разновидность управления по эталонной модели (model matching control). Также отмечается, что основной вклад внешних сил вносит не гидродинамическая сила сопротивления окружающей жидкости, а сила за счет присоединенной массы воды.

В [58], наоборот, приведен случай гидравлического подводного манипулятора с доминирующими воздействиями от гидродинамических сил. Применяется итеративный алгоритм расчета динамики Ньютона-Эйлера и предлагается подход к управлению по обратной модели динамики. Основным недостатком является требование точного знания динамической модели, что редко доступно (почти невозможно) на практике. Поэтому в рамках данного подхода сложно обеспечить робастность к неточности модели и внешним возмущениям [37].

С целью разработать регулятор, который может противодействовать эффектам неполной компенсации, вызванной переменными параметрами и возмущениями, учитывая нереалистичное предположение о точном знании параметров модели динамики подводного манипулятора, некоторые исследователи применили робастные и адаптивные стратегии управления. Первый подход стремится минимизировать эффекты неточности аппроксимации модели на качество управления, а второй адаптирует параметры модели к параметрам реального подводного манипулятора [37]. Общей тенденцией в этой группе является использование упрощенной модели манипулятора (и/или среды) и оценка возмущающих воздействий (явная или неявная), чтобы парировать сильно нелинейную и переменную динамику системы.

Так, в [39] предложен робастный регулятор, комбинирующий централизованное управление манипулятором по предрассчитанным моментам (computed torque), и регулятор на скользящем режиме. Дополнительно нейросетевой регулятор обеспечивает устойчивость, в случае больших начальных рассогласований и несоответствий модели.

Подход [40] предлагает другую робастную схему, включающую наблюдатель возмущений, который «преобразует» нелинейную модель подводного манипулятора со всеми неточностями в простую модель с ошибкой по возмущению, к которой уже применяется беспоисковый адаптивный регулятор.

В работах [41, 42] авторы также предлагают робастный регулятор для движения по траектории на основе скользящего режима и динамической модели, для оценки внешних возмущений.

ПД-регулятор с наблюдателем состояния и back-stepping подходом к линеаризации для подводного манипулятора рассматривается в [43].

Еще один регулятор на скользящих режимах предложен в [44], где используется наблюдатель возмущений, агрегирующий в себе компенсационный сигнал для возмущений и неточностей модели.

Регулятор с оценкой возмущений из [45] использует приближенную модель динамики для вычисления модельного компенсационного сигнала и частичного развязывания переменных состояния. Предрассчитанный сигнал по положению/скорости используется в прямом канале, а через наблюдатель оцениваются внешние возмущения совместно с ошибками в модели динамики и заводятся в компенсационный контур. Дополнительно нелинейный ПД-регулятор используется во внешнем контуре с двумя целями: улучшить динамику переходных процессов и стабилизировать замкнутую систему, а также применяется в качестве сигнала оценки неточности модели внешних возмущений.

Регуляторы на скользящих режимах (как и, в принципе, регуляторы с переменной структурой, использующие скачкообразное переключение между режимами/регуляторами) генерируют колебания в системе вследствие переключения. В работах [46,47] рассматривается снижение колебаний из-за переключения режимов за счет различных стратегий переключения.

Нейросетевые и нечетко логические подходы также рассматривались рядом автором [48– 50]. Нейронные сети используются для аппроксимации сложной нелинейной динамики подводных (и/или гидравлических) манипуляторов в контуре компенсации, а нечетко логические схемы для адаптации коэффициентов ПИ/ПД-регуляторов.

Борьба с колебаниями

Несмотря на наличие большого количества потерь в гидравлических системах, они обладают повышенной колебательностью. Основные причины колебательных явлений связаны с упругими свойствами жидкости и стенок трубопровода, инерциальными свойствами самой рабочей жидкости, а также нелинейным характером процессов в элементах гидропривода. При наличии паразитных связей в элементах гидропривода (например, питающей цепи и различных ступеней многоступенчатого дросселя) колебания могут усиливаться, достигая цепей управления. Добавление в систему схем, обеспечивающих повышение энергоэффективности, также приводит к увеличению колебательности.

Два типа методов демпфирования были предложены в литературе: чисто гидравлические и электрогидравлические. В чисто гидравлическом методе применяется настройка (и/или введение) гидравлических элементов, обеспечивающих демпфирование, но динамическое поведение оптимизировано только под одну рабочую точку без адаптации [11]. Электрогидравличе-ский метод может быть применен без добавления новых гидроэлементов за счет управления имеющимися дросселями и насосами, с введением дополнительных обратных связей по давлению, скорости/ускорению течения жидкости. Применение линейных регуляторов ([12,51]), так же как и настройка гидросистемы, носит локальный характер (вблизи рабочей точки) и пло- хо применимо к сложным системам (типа манипуляторов) с большим диапазоном изменяющихся параметров.

Регуляторы на основе предикативного управления [14] и поиска экстремума [52] позволяют бороться с колебаниями при не очень быстрых сменах внешней нагрузки. В [53] предложен метод с почти гарантированным размещением доминантных полюсов в системе (может быть получено субоптимальное демпфирование).

Проблема гашения колебаний является острой в системах гидропривода. Она «дуальна» к проблеме быстродействия. Быстрые процессы, как правило, сопровождаются большей колебательностью системы. То же можно сказать про обеспечение энергоэффективности в гидросистемах с регенерацией/рекуперацией энергии за счет более сложной динамики самого объекта. Гашение колебаний нагрузки сопряжено, в свою очередь, с меньшей энергоэффективностью, т.к. требуется задействовать гидравлические контуры, что приводит к повышению расхода и, следовательно, потерям.

Проблема снижения колебаний, хоть и не является центральной в области, но все еще представляет сложности и служит областью текущих исследований.

Энергоэффективность и средства ее обеспечения

Разработка электрогидравлических компонентов и систем открывает новые возможности для дальнейшего повышения энергоэффективности и удобства эксплуатации. Разработки направлены на достижение высокой энергоэффективности с хорошей управляемостью. Однако на коммерческом рынке существенным ограничением является стоимость (а, следовательно, и сложность системы). Хотя доверие к надежности электрогидравлических систем растет, управление электрогидравлическими системами требует дальнейших исследований, прежде чем оно станет адаптивным и надежным в реальных условиях работы мобильных и стационарных установок.

В последние десятилетия наблюдается увеличение запроса на энергосбережение, что служит мотивацией для разработки новых электрогидравлических систем. Было предложено несколько усовершенствованных схем управления, и их энергосберегающий потенциал был подтвержден с помощью моделирования и реальных испытаний. Однако ни одна из этих энергоэффективных схем не нашла широкого применения из-за роста стоимости, плохой управляемости или низкой надежности. Тем не менее одним обнадеживающим применением является гибридное управление (стремящееся достичь энергоэффективности за счет регенерации и рекуперации энергии); однако это приложение по-прежнему неудовлетворительно из-за увеличения стоимости и высокого уровня обслуживания. Прежде чем применять усовершенствованные схемы управления, необходимо найти приемлемый компромисс между энергосбережением и другими требованиями. Например, управление переключением насосов [54] является потенциальным решением из-за высокой стоимости системы с регулируемым рабочим объемом, но необходимо дальнейшее развитие метода управления потоком и переключением для достижения надежной работы, приемлемой стоимости и хорошей управляемости.

Можно выделить следующие группы методов организации гидросистемы и управления, обеспечивающие экономию энергии [33] (рис. 4):

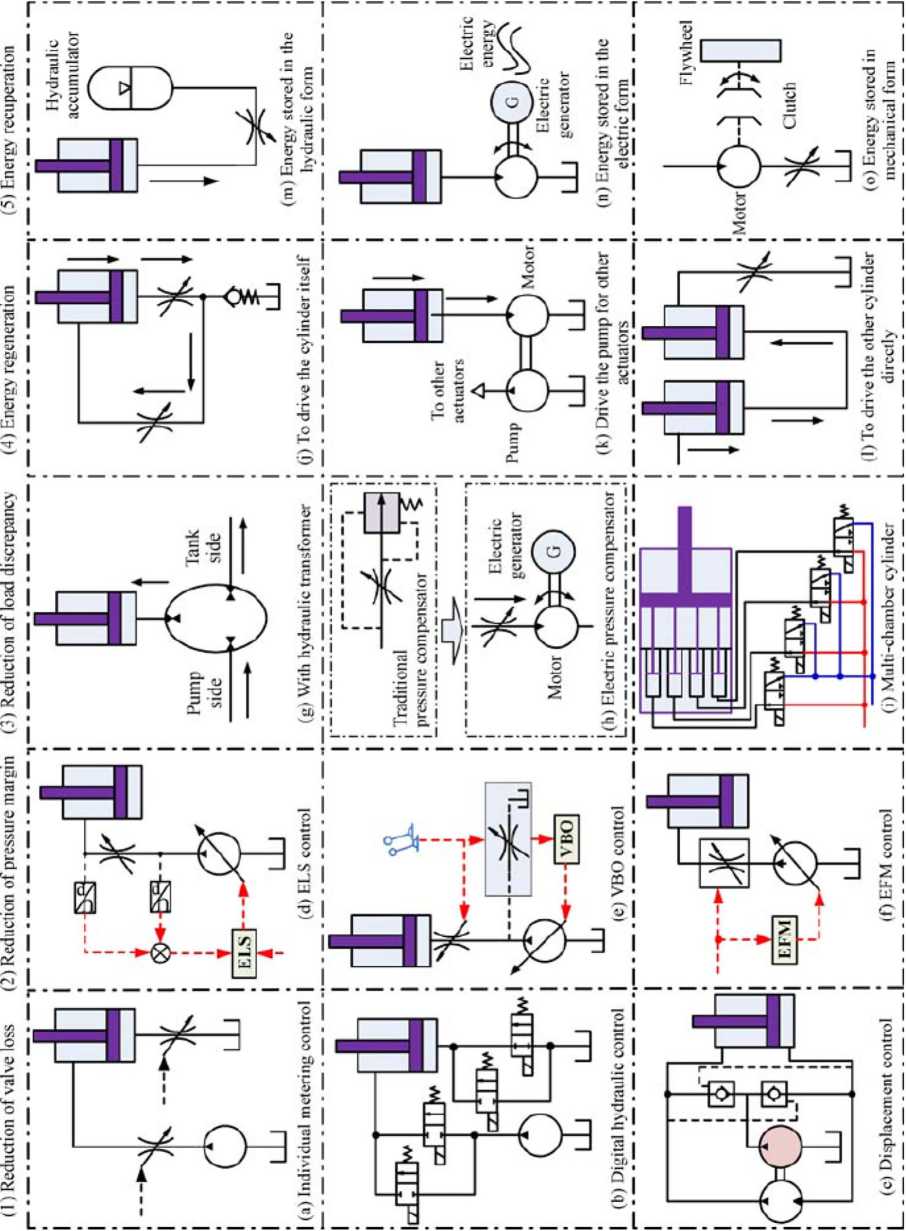
Рис. 4. Схемы снижения потерь энергии в системах гидропривода ([33])

Fig. 4. Schemes for reducing energy losses in hydraulic drive systems ([33])

• –    индивидуальное управление дросселями в линии высокого и низкого давлений;

• –    использование нескольких параллельных дросселей, работающих в дискретном режиме открыт/закрыт (т.н. дискретное управление);

• –    регулируемый насос, управляемый внешним приводом сообразно с необходимым требуемым движением гидравлического актуатора.

• 2.    Снижение потерь на запас по давлению

Гидронасос, работающий на редуктор давления, создает магистральное давление в системе. Если это давление сильно превышает требуемое давление в системе (сопротивление в элементах и магистралях и внешнее давление), то его необходимо дополнительно уменьшать, сбрасывая его на дросселях и других управляющих элементах, что и приводит к возникновению потерь. Следующие схемы применяются для снижения потерь:

• –    обратная связь по нагрузке (электрическая/механически-гидравлическая);

• –    снижение потерь за счет исключения гидравлического редуктора давления путем регулирования насоса с измерением давления в магистрали и расчета требуемого давления в системе при сохранении податливости системы по внешнему усилию (VBO – Virtual bleed off [55]);

• –    отработка требуемого потока за счет правильного расчета и управления в электроги-дравлической системе (фактически насос управляется в режиме постоянного расхода, рассчитываемого системой управления в зависимости от требуемого движения манипулятора).

• 3 . Снижение разницы в нагрузке

Источник давления (как правило, один на систему) создает магистральное давление для нескольких абонентов. Если сила/момент или расход у абонентов разный, то КПД всей системы обратно пропорционально разности давлений (при одинаковом расходе), т.к. на абонентах с меньшей внешней нагрузкой приходится прикрывать дроссель и увеличивать паразитное падение давления на нем. Решением данной проблемы могут быть:

• –    применение гидравлических преобразователей давления/расхода;

• –    преобразование избыточного давления в другие виды энергии (электрическую, чаще всего);

• –    использование сегментных цилиндров (или нескольких вращающихся гидромоторов на одном валу) с независимым питанием и управлением, суммирующими усилие/момент.

• 4.    Регенерация энергии

Под регенерацией энергии авторы [33] подразумевают использование энергии одного гидравлического актуатора для питания другого. Это может быть сделано различными способами:

• –    использованием давления, развиваемого внешней силой на гидроактуаторе, для осуществления движения самого гидроактуатора (замыкание гидроактуатора самого на себя);

• –    прямым соединением одного гидроактуатора с другим (внешнее давление/движение передается в другой гидроактуатор без преобразования или трансмиссии);

• –    передачей энергии в общий гидронасос (через подключение к промежуточному гидромотору).

• 5.    Рекуперация энергии

При регенерации энергии она нигде не запасается, а мгновенно передается в другие гидроактуаторы системы.

Рекуперация энергии связана с возвратом избыточной или внешней энергии в источник. Рекуперированная энергия может запасаться или расходоваться непосредственно. Рекуперированная энергия из «гидравлической» (как правило) преобразуется в другие виды (электри-ческой/механической) или сохраняется в исходной форме (например, в гидроаккумуляторах).

Указанные подходы реализуются через применение достаточно сложных гидравлических схем и алгоритмов управления. Основные сложности возникают за счет того, что система включает в себя дополнительные элементы, которые увеличивают порядок системы и связность (взаимовлияние) между степенями свободы, вследствие чего происходит:

– увеличение колебательности,

– появление дополнительных паразитных связей между степенями свободы,

– (как следствие) усложнение алгоритмов управления.

В статье рассмотрены некоторые вопросы применения гидравлических манипуляторов в радиационных и подводных средах. Проведен обзор методов моделирования гидравлических манипуляторов и подходов к управлению.

Гидравлические манипуляторы хорошо подходят для работы в зонах с высокой радиацией, т.к. большая часть их компонент (кроме, возможно, прокладок из полимерных материалов) выдерживают высокие дозовые нагрузки. Сложным остается вопрос датчиковой аппаратуры, определяющей положение и/или контактные усилия в степенях подвижности манипулятора, расположенных непосредственно в зоне радиационного воздействия. Наибольшему воздействию подвергаются электронные узлы и изоляция проводников. Полупроводниковые приборы оказываются наиболее уязвимыми к воздействию гамма-излучения. Для защиты электроники необходимо предусматривать дополнительные слои защиты и применять соответствующие схемотехнические решения, либо выносить обрабатывающую электронику за пределы зон высокой радиации.

Обзор моделей гидропривода и гидроманипуляторов показал высокую нелинейность и взаимосвязи обобщенных координат. Кроме того, во многих источниках говорится о принципиальной невозможности точно смоделировать динамику гидросистемы, и часть ее остается не описанной и не реализованной в явном виде в моделях. Некоторые параметры известной части моделей не могут быть получены теоретически, а только путем экспериментального замера (фактические гидравлические сопротивления гидролиний, коэффициент утечек и параметры дросселей).

Модель манипулятора с гидроприводом состоит из уравнений твердотельной динамики и уравнений гидропривода. Динамика гидропривода оказывается в несколько раз быстрее, чем твердотельная динамика звеньев манипулятора. Связь между степенями подвижности манипулятора с гидроприводом происходит по двум каналам: неинерциальные силы, возникающие при движении кинематической цепочки твердых тел, и через общие участки гидролинии. В подводных манипуляторах дополнительно появляются внешние гидродинамические силы, – 336 – которые нельзя представить в конечном формульном представлении. Точное моделирование этих сил сопряжено с высокими вычислительными затратами и, как правило, аппроксимируется в некоторой области.

В силу нелинейности модели и неизбежного наличия неучтенных процессов в моделях динамики системы управления должны учитывать эту неопределенность и обеспечивать устойчивость и качество процессов регулирования. Обзор существующих схем управления показал тенденцию к прямой компенсации и развязыванию части переменных состояния через известную часть модели динамики. Оставшаяся часть моментов, не вошедших в модель, компенсируется через механизм адаптации. Широкое применение нашел метод адаптивного управления по эталонной модели и его вариации, а также схемы с оценкой возмущений. Нейронные сети также используются в качестве неявных моделей/компенсаторов неизвестной части динамических процессов. Робастные схемы на основе скользящих режимов и нечетких множеств также нашли применение.

Отдельным аспектом управления гидравликой представлены схемы повышения энергоэффективности. Низкий КПД гидропривода, обусловленный утечками и вязким трением в элементах и гидролиниях, делает его малопривлекательным в задачах мобильной робототехники и там, где важна экономия энергии. Рассматриваются несколько источников потерь (на дросселирование, чрезмерный запас по давлению, разница в нагрузке разных актуаторов в общей гидролинии) и методы борьбы с ними, а также подходы к регенерации и рекуперации энергии.

• [1]    Hollerbach J., Hunter I., Ballantyne J. A Comparative analysis of actuator technologies for robotics. Robotics Rev . 2, 1992, 299–342.

• [2]    Power and torque density [Electronic resourse] – Access: https://www.emobility-engineering . com/challenge-of-power-torque-density/

• [3]    Бондарева Н. В. и др. Сверхвысоковакуумные жидкости для открытых космических систем отвода низкопотенциального тепла. Вестник Московского авиационного института , 2012, Т-19,3, 54–61 [Bondareknko N. V. Superhighvacuum liquids for the space system of thermal conduction for low potential heat, Vestnik of Moscow aviation institute , 2012, Т-19,3, 54–61 (inRus.)]

• [4]    Siciliano B. and Khatib O. Springer Handbook of Robotics . Secaucus. NJ, USA: SpringerVerlag New York, Inc., 2007, 2227.

• [5]    Magana B., Sangiah O., etc. Highly-Integrated Hydraulic Smart Actuators and Smart Manifolds for High-Bandwidth Force Control. Frontiers in Robotics and AI , 2018, 5.

• [6]    Merritt H. E. Hydraulic Control System , John Wiley, New York, 1967.

• [7]    Whitcomb L. L. (n.d.). Underwater robotics: out of the research laboratory and into the field . Proceedings 2000 ICRA. Millennium Conference. IEEE International Conference on Robotics and Automation. SymposiaProceedings (Cat. No.00CH37065). doi:10.1109/robot.2000.844135

• [8]    Окорочков В.В., Окорочкова В. М., Шафранов В. В. Актуальность и направления развития роторно-поршневой тематики. Вестник Самарского университета. Аэрокосмическая техника, технологии машиностроения , 2014, 13(5–3), 82–91 [Okorochkov V. V., Okorochkova V. M., Shafranov V. V. Relevance and directions of development of rotary-piston themes. Bulletins of Samara University. Aerospace Engineering, Technology and Mechanical Engineering , 2014, 13(5–3), 82–91 (in Rus.)]

• [9]    Robaid: SAUVIM robot completed its first fully autonomous mission (2022) [Electronic resourse] – Access: http://www.robaid . com/robotics/sauvim-robot-completed-its-first-fully-autonomous-mission.htm

• [10]    Autonomous Underwater Intervention: the SAUVIM Project [Electronic resourse] – Access: https://gmarani.org/na/sauvim/index.html

• [11]    Sivčev S., Coleman J., Omerdić E., Dooly G., Toal D. Underwater manipulators: A review. Ocean Engineering , 2018, 163, 431–450.

• [12]    Ishitsuka M., Ishii, K. Development and control of an underwater manipulator forAUV, Prog. of 2007 Symposium on Underwater Technology and Workshop on ScientificUse of Submarine Cables and Related Technologies , 2007, 337–342.

• [13]    Ishitsuka M., Ishii K., 2007b. Modularity development and control of an underwater manipulator for AUV. Proc. of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems , 2007, 3648–3653.

• [14]    Hildebrandt M., Kerdels J., Albiez J., Kirchner F. A multi-layered controller approach for high precision end-effector control of hydraulic underwater manipulator systems. Proceedings of the OCEANS 2009 , 2009 1–5.

• [15]    Ou Y., Xu B., Cai H., Zhao J., & Fan J. (2022). An overview on mobile manipulator in nuclear applications. 2022 IEEE International Conference on Real- time Computing and Robotics (RCAR) , 2022, 239–243.

• [16]    Bogue R. Robots in the nuclear industry: a review of technologies and applications. Industrial Robot: An International Journal , 2011, 38(2), 113–118.

• [17]    Smith J. S., Yu R., Sarafis I., Lucas J. Computer vision control of an underwater manipulator. Proceedings of the OCEANS ’94. ’Oceans Engineering for Today’s Technology and Tomorrow’s Preservation’ ,1994. 1. 187–192.

• [18]    Bakari M., Zied K., Seward D. Development of a Multi-Arm Mobile Robot for Nuclear Decommissioning Tasks. International Journal of Advanced Robotic Systems. , 2007, 4. 10.5772/5665.

• [19]    Dunnigan M. W., Lane D. M., Clegg A. C., Edwards I. Hybrid position/force control of a hydraulic underwater manipulator. IEE Proc. Contr. Theor. , 1996, Appl. , 143(2), 145–151.

• [20]    Lu C., Yang T., Jin K., Gao N., Xiu P., Zhang Y., Wang L. Radiation-induced segregation on defect clusters in single-phase concentrated solid-solution alloys . Acta Materialia, 2017, 127, 98–107

• [21]    Дубровский В. Б. [и др.] Радиационная стойкость материалов : справочник: под ред. В. Б. Дубровского. М., Атомиздат, 1973, 262. 547 [Dubrovsky V. B. [et al.] Radiation resistance of materials , reference: ed. by V. B. Dubrovsky. M., Atomizdat, 1973, 262, 547]

• [22]    Безродных И.П., Тютнев А. П., Семёнов В. Т. Радиационные эффекты в космосе . Открытое АО «Науч.-произв. корпорация «Космические системы мониторинга, информ.-управ-ляющие и электромеханические комплексы им. А. Г. Иосифьяна, Москва. Корпорация «ВНИ-ИЭМ», 2014, 25 [Bezrodnykh I. P., Tyutnev A. P., Semenov V. T. Radiative effect sin space .Open JSC «Nauch.-prosv. Corporation “Space monitoring systems, inform.-control and electromechanical complexes named after A. G. Iosifyan, Moscow, Corporation “VNIIEM”, 2014, 25(in Rus.)]

• [23]    Листы на основе терморасширенного ГРАФИТА (ТРГ) [Электронный ресурс] – Режим доступа: https://germett.ru/listyi-na-osnove-termorasshirennogo-grafita-trg/ – Заглавие с экра-

• на. [Sheets based on thermally expanded GRAPHITE (TRH)] – Access: https://germett.ru/listyi-na-osnove-termorasshirennogo-grafita-trg/

  • [24]    Krause P. C., Wasynczuk O., Sudhoff S., Pekarek P. Analysis of electric machinery and drive systems. Third edition, John Wiley & Sons, Inc., Hoboken, New Jersey, USA, 2013. 676.

  • [25]    Jelali M., Kroll A. Hydraulic Servo-systems. Advances in Industrial Control., 2003, doi:10.1007/978–1–4471–0099–7.

  • [26]    Dorr H. et al. Hydraulic Trainer, Volume 2: Proportional and Servo Valve Technology. Mannesmann Rexroth, USA, 1986. 265.

  • [27]    Mamèic S., & Sogdevièius, M. Simulation of dynamic processes in hydraulic accumulators. Transport, 2010, 25(2), 215–221.

  • [28]    Goebel F., Sanfelice R. G., Teel A. Hybrid dynamical systems. IEEE Control Systems,2009, 29(2), 28–93.

  • [29]    Duindam V., Macchelli A., Stramigioli S., &Bruyninckx H. Port-Based Modeling of Dynamic Systems. Modeling and Control of Complex Physical Systems, 2009, 1–52.

  • [30]    Liceaga-Castro E., Qiao H., Liceaga-Castro J. Modelling and control of a marine robot arm. Proceedings of the 30th IEEE Conference on Decision and Control, 1991, 1, 704–705.

  • [31]    Cuadrado J., Naya M., Dopico D. D., Lugrís U. Efficient augmented Lagrangian formulation for the combined simulation of multibody and hydraulic dynamics. 5th Asian Conference on Multibody Dynamics 2010, 280–290.

  • [32]    Rahikainen J., González F., Naya M. Á., Sopanen J., &Mikkola A. On the cosimulation of multibody systems and hydraulic dynamics. Multibody System Dynamics, 2020, doi:10.1007/s11044– 020–09727-z.

  • [33]    Xu B., Cheng M. Motion control of multi- actuator hydraulic systems for mobile machineries: Recent advancements and future trends. Front. Mech. Eng. 13, 2018, 13, 151–166.

  • [34]    Huova M. Energy efficient digital hydraulic valve control. Dissertation for the Doctoral Degree. Tampere: Tampere University of Technology, 2015.

  • [35]    Manring N. D., Mehta V. S. Physical limitations for the bandwidth frequency of a pressure controlled, axial-piston pump. Journal of Dynamic Systems, Measurement, and Control, 2011, 133(6), 50–62.

  • [34]    Grabbel J., Ivantysynova M. An investigation of swash plate control concepts for displacement controlled actuators. International Journal of Fluid Power, 2005, 6(2), 19–36.

  • [37]    Siciliano B., Sciavicco L., Villani L., Oriolo G. Robotics Modelling, Planning and Control. Springer-Verlag London, 2009. 623.

  • [38]    Yao J., Wang C. Model reference adaptive control for a hydraulic underwater manipulator. J. Vib. Contr.,2012, 18(6), 893–902.

  • [39]    Lee M., Choi H.-S. A robust neural controller for underwater robot manipulators. IEEE Trans. Neural Network, 2000, 11(6), 1465–1470.

  • [40]    Yuh J., Zhao S., Lee P. M. Application of adaptive disturbance observer control to an underwater manipulator. Proceedings of the IEEE International Conference on Robotics and Automation, 2001 ICRA,2001, 4, 3244–3249.

  • [41]    Kwon D.S., Ryu J. H., Lee P. M., Hong S. W. Design of a teleoperation controller for an underwater manipulator. Proceedings of the IEEE International Conference on Robotics and Automation, 2000 ICRA. Millennium Conference, 2000, 4, 3114–3119.

  • [42]    Xu G., Xiao Z., Guo Y., Xiang X. Trajectory tracking for underwater manipulator using sliding mode control. Proceedings of the 2007 IEEE International Conference on Robotics and Biomimetics (ROBIO), 2007, 2127–2132.

  • [43]    Mohan S., Kim J. Robust PID control for position tracking of an underwater manipulator. Proceedings of the 2015 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), 2015, a. 1707–1712.

  • [44]    Venkatesan V., Mohan S., Kim J. Disturbance observer based terminal sliding mode control of an underwater manipulator. Proceedings of the 2014 13^th International Conference on Control Automation Robotics Vision (ICARCV), 2014, 1566–1572.

  • [45]    Mohan S., Kim J. Robust PID control for position tracking of an underwater manipulator. Proceedings of the 2015 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), 2015, a. 1707–1712.

  • [46]    Ding R., Xu B., Zhang J., et al. Bumpless mode switch of independent metering fluid power system for mobile machinery. Automation in Construction, 2016, 68, 52–64.

  • [47]    Xu B., Cheng M., Yang H., et al. A hybrid displacement/pressure control scheme for an electrohydraulic flow matching system. IEEE/ASME Transactions on Mechatronics, 2015, 20(6), 2771–2782

  • [48]    Wang L., Wang C., Wang W., Wang C. A novel hybrid control method for the underwater manipulator. 2008 International Workshop on Education Technology and Training, 2008 International Workshop on Geoscience and Remote Sensing, 2008, 1, 790–794.

  • [49]    Suboh S.M., Rahman I. A., Arshad M. R., Mahyuddin M. N. Modeling and control of 2-DOF underwater planar manipulator. Indian J. GeoMar. Sci., 2009, 38, 365–371.

  • [50]    Pandian S.R., Sakagami N. A neuro-fuzzy controller for underwater robot manipulators. Proceedings of the 2010 11th International Conference on Control Automation Robotics Vision, 2010, 2135–2140.

  • [51]    Zaev E., Rath G., Kargl H., et al. Energy efficient active vibration damping. Proceedings of the 13th Scandinavian International Conference on Fluid Power. Linköping, 2013, 355–364

  • [52]    Fossen T. I. Handbook of marine Craft Hydrodynamics and Motion Control. John Wiley & Sons, 2011, 582.

  • [53]    Khalil W., Dombre E., 2004. Modeling, Identification and Control of Robots. Butterworth-Heinemann, 2004, 483.

  • [54]    Kim Y.-B., Kim P.-Y., Murrenhoff H. Boom Potential Energy Regeneration Scheme for Hydraulic Excavators. BATH/ASME 2016 Symposium on Fluid Power and Motion Control, 2016.

  • [55]    The Drive & Control Company. Virtual bleed off VBO. Retrieved – Access: https://dc-corp. resource.bosch.com/media/xc/company_1/press/product_information/product_information_2013/ pi_april_2013/PI_032_13_VBO_en.pdf

  • [56]    Clegg A. C., Dunnigan M. W., Lane D. M. Self-tuning position and force control of an underwater hydraulic manipulator. Proceedings of the 2001 ICRA. IEEE International Conference on Robotics and Automation, 2001, 4, 3226–3231.

  • [57]    Xu B., Sakagami N., Pandian S. R., Petry F. A fuzzy controller for underwater vehiclemanipulator systems. Proceedings of the OCEANS 2005 MTS/IEEE,2005, 2, 1110–1115

  • [58]    Schjølberg I., Fossen T. I. Modelling and control of underwater vehicle-manipulator systems. Proceedings of the 3rd Conference on Marine Craft Maneuvering and Control, 1994.