Гидроструйный эжекционный гидрометатель сыпучих материалов. Метод расчета

Принципиальная схема струйного насоса — гидрометателя приведена на рис 1 [1]. Струя воды из сопла 1 устремляется в камеру смешения 2 и увлекает пульпу (сыпучий материал в смеси с водой) из бункера 3. В камере 2 происходит смешение двух потоков и образование высокоскоростного потока гидросмеси [1, 4]. Дальность полета струи гидросмеси зависит от ее скорости в выходном сечении смесительной камеры [2, 5]. Задача расчета гидрометателя состоит в том, чтобы при заданных дальности полета пульпы, подачи сыпучего материала и его физических свойств определить основные размера гидрометателя, при которых энергопотребление на его работу будет минимальным [2-5, 13].

Рис. 1. Схема гидрометателя

Основными соотношениями для расчета оптимального гидрометателя являются уравнения дальности полета струи гидросмеси и характеристики гидрометателя, а также выражение для ко-

Расчет и конструирование

эффициента эффективности гидрометателя, равного отношению кинетических энергий струй гидросмеси на выходе из аппарата и активного потока (воды) на срезе сопла [1, 2].

В безразмерных координатах уравнение характеристики имеет вид [1]:

с2

-р* - 1)+Ар« + 1) + 4Al1 + р||гу^-11 \            к вЛ^в 7

ГУ = ---------------"-----------7------—-------------------- * max                               /       \                       ^;

2 р11 + с I\ в 7 в = 2 + Ztp 1 - Z вх - 2^ (1 -< где а - коэффициент эжекции, равный отношению объёмных расходов эжектируемой гидросмеси и струи активного потока; р = р / р - относительная плотность пассивного потока (гидросмеси) во входном бункере; р - плотность воды; р - плотность эжектируемой гидросмеси; р, = р / р - относительная плотность гидросмеси на выходе из гидрометателя; р - плотность гидросмеси на выходе из гидрометателя; q = a0 / А2 - относительная площадь сопла; Ао и А2 - площади выходного сечения сопла и нормального сечения смесительной камеры; £тр, Z вх - коэффициенты сопротивления смесительной камеры и входа в камеру.

Зависимость коэффициента эффективности гидрометателя от относительной площади сопла при нескольких значениях относительной плотности эжектеруемой гидросмеси представлены на рис. 2.

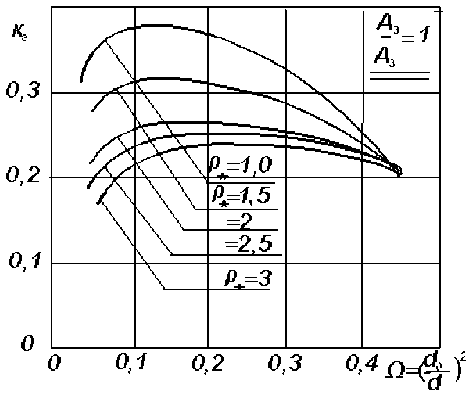
Рис. 2. Влияние размеров аппарата и соотношения плотностей потоков на коэффициент эффективности

Например, при относительной плотности эжектируемой гидросмеси р = 2 наибольшая эффективность аппарата достигается при О = 0,2 . Этой относительной площади соответствует максимальный коэффициент эжекции а = 0,92 . Таким образом, зная относительную плотность р гидросмеси во входном бункере, определяем по графикам на рис. 2 оптимальную относительную площадь сопла П_о (при которой коэффициент эффективности наибольший), и по уравнению (2) -максимальный коэффициент эжекции а [1, 3, 4, 16]. Имея величину расхода эжектируемой пульпы Q_n, можно найти расход гидросмеси на выходе из гидрометателя по формуле:

_ а + 1

Q CM =      Q n .

а

Как показали экспериментальные исследования [6-12], для равномерной загрузки гидрометателя необходимо подавать твердую фракцию в смеси с водой, причем расход воды Qnoдn дол- жен составлять (68…70) % от расхода сыпучего материала Qт. Следовательно, расход подпитки равен:

а расход пассивного потока: Q П = Q t + Q nodn .

При этом относительная плотность эжектируемой гидросмеси:

Q подп . ρ _ж + Q_Т . ρ гр ρ ∗ =

.

Q _Π ρ _ж

По известной дальности укладки Χ и вычисленному значению расхода эжектируемой гидросмеси при данном коэффициенте эжекции а из расчета дальности струи по формулам [2]:

Χ

Хк = 1  л К^  ; X = 2HSin 2в;

• к 1 + 0,63ψ

• у = /Х.   .te----,(

d    ρ ж    1 + Sin β

• 1    - Sin β

можно вычислить диаметр d рабочей камеры гидрометателя. Диаметр d0 сопла активного потока будет определяться по формуле:

d0 = d Vq .

Здесь H = —--скоростной напор струи гидросмеси на выходе из рабочей камеры; 2 g

Р и р - плотности воздуха и воды, в — угол наклона оси рабочей (смесительной) камеры гидрометателя; X - коэффициент гидравлического трения. Режим работы гидрометателя определяется расходом Q₀ и напором Н₀ активного потока на срезе сопла, которые найдутся из соотношений:

qО = Q;

α

H = ^{υ 20}

0    _{2 g}

8 Q 0²

g n ² d 0 .

Мощность активного потока перед соплом гидрометателя равна: ρ ₀ gQ ₀ H ₀ N          2      ,

ϕ ²

где ф — коэффициент скорости сопла активного потока, g — ускорение свободного падения.

Выполняя расчет для ряда значений коэффициента а , выбираем наиболее приемлемый режим работы гидрометателя и соответствующие этому режиму значения диаметров сопла и рабочей камеры.

Чтобы воспользоваться формулами (5), (6) расчета струи, необходимо знать коэффициент трения λ. В первом приближении для определения коэффициента λ можно воспользоваться опытами, проведенными различными авторами на свободных водяных струях [2, 5-7]. Используя эти эксперименты, установили, что коэффициент трения зависит главным образом от двух парамет- 2

ров: от угла наклона оси камеры в и от отношения H где H = -2-, d - диаметр выходного се-d ,         2g чения рабочей камеры. Причем заметное влияние угла струи на коэффициент трения наблюдается только при углах в < 32°. На рис. 3 представлен график зависимости коэффициента X от от ношения H построенный по опытным данным [5-7], с использованием формул (4), (5). d

Расчет и конструирование

Как видим, коэффициент гидравлического трения струи в воздухе практически одинаков при одном и том же отношении H как при в = 30°,,, 32°, так и при в = 15°.

Таким образом, формулы расчета свободной струи, дополненные графиком зависимости

X = / (H/d) (см. рис. 3) позволяют провести расчет струи и определить диаметр рабочей камеры по дальности полета струи и расходу гидросмеси.

Объединим формулы (5) и (6) в одно общее выражение:

Χ

к

2 HSin 2 β

1 + 2,52λ⋅ ρв ρ

ж

H Sin ² β ⋅⋅

d    1 + Sinβ г n--------

1 - Sinβ

из которого видно, что на дальность полета струи Χ угол β оказывает большое влияние. Как показали лабораторные испытания гидрометателя и рекомендации других авторов [2, 5, 6,19], наибольшая дальность полета достигается при углах в = 30°,,, 35°. Подставив в формулу (9) в = 30° после вычислений, получим:

Χк

тах

1,732H

1 + λ⋅ ρВ ρ0

⋅ H ⋅ 0,573 d

Напор струи Н на выходе из рабочей камеры можно выразить через расход смеси и диаметр рабочей камеры по формуле:

H = 8^ = 0,0825 Q2^.                                          (9)

g π ² d ⁴           d

Отношение плотности р_в воздуха к плотности р₀ жидкости (воды) в первом приближении равно 1,25 - 10 - 3 .

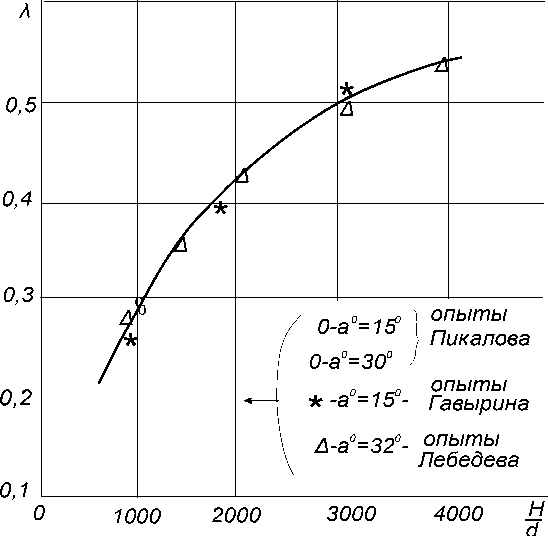
Рис. 3. Зависимость коэффициента трения от отношения напора к диаметру 4

Тогда уравнение (8), после некоторых преобразований с использованием равенства (9), можно записать так:

^{Х К} тах

0,143 ^Q ₄

.

1 + 5,9 •Ю 5 1 • Q^ ^,              d ⁵

По этому уравнению и графику х = у | H | на рис. 4 построены графики для определения диа-I d )

метра рабочей камеры гидрометателя d в зависимости от расхода гидросмеси Qсм и требуемой дальности полета струи. Этот график значительно упрощает расчет гидрометателя.

Пример расчета гидрометателя

Рассчитаем гидрометатель при расходе гравия Q т = 53 м ³ /час и дальности укладки Хк =

50 М. По формуле (2) определяем расход подпитки:

Qnodn = 0,70 • 53 = 36,6[м3 / час], а по формуле (3) - расход пассивного потока:

Q _n = 53 + 36,6 = 89,6 м ³ / час = 2,49 • 10 ^{- 2}, м 3 .

с

Плотность пассивного потока, как это следует из выражения (4), равна:

Р . =

36,6 - 10³ + 53 • 2,65 - 10³

= 2,0.

89,6 - 10³

Учитывая коэффициент эжекции из формулы (1), определим режим работы гидрометателя. Как было показано выше, наибольшая эффективность гидрометателя достигается при α = 0,92. Примем это значение коэффициента эжекции за расчетное и определяем соответствующее значение основного геометрического параметра Q = 0,2. Расход гидросмеси на выходе из гидрметателя найдем по формуле:

Q = 1 ± °92 • 89,6 = 187 [ м ³ / час ] .

^см 0,92

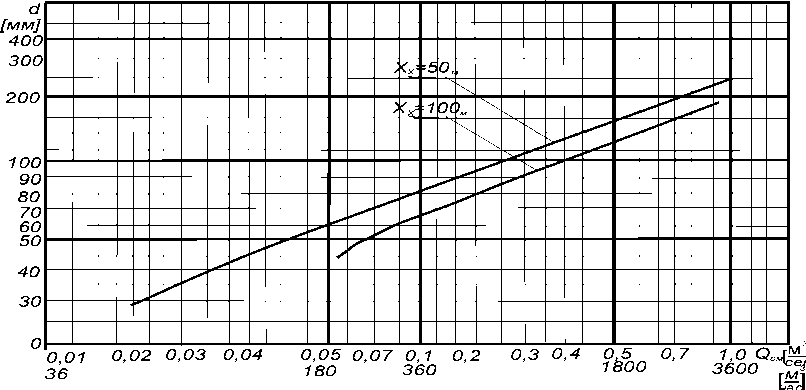
Рис. 4. Вспомогательный график к расчету диаметра рабочей камеры

Зная расход гидросмеси и дальность укладки Х_к = 50_м, по графику на рис. 4 находим диаметр рабочей камеры гидрометателя d = 62,0 [мм], диаметр выходного сечения сопла активного потока d ₀ = 62,070,2 = 27,9 [ мм ] , расход и напор активного потока:

q = 2,4910   = 2,71 • 10 -2 [м3/ сек],

0      0,92       , н = 8Q,2  _      8 • 2,712 •Ю-4

58,75 •Ю ^{- 4}

58,61 • 10 ^{- 6}

= 100 [ м ] .

⁰    дп 2 d₀⁴    9,81 • 3,14 ² • 2 • 27,9 4 • 10 ^{- 8}

Расчет и конструирование

Мощность активного потока перед соплом гидрометателя:

_{N =} ρ 0 gQ 0 H 0    10³ ⋅ 9,81 ⋅ 2,71 ⋅ 10 ^{- 2} ⋅ 100         _кВт.

υ ²                  0,95^{2               ,}

Как видим, при оптимальном режиме работы гидрометателя (α = 0,92 ; Ω = 0,2) необходим напор активной жидкости H 0 = 100 м. Остальные размеры проточной чисти гидрометателя определяем по рекомендациям, изложенным в книгах [3, 4, 15, 17, 20].

Выводы

Предложен метод расчета гидроструйного эжекционного гидрометателя с минимальными расходами воды и энергии при заданных подаче и дальности полета твердого сыпучего материала.