Гладкие методы в многокритериальных задачах

Под конечномерной многокритериальной моделью мы будем называть математическую модель с N целевыми функциями

F k (ж, u) ^ max,      к = [1,N] ,                            (1)

X подлежащими максимизации на. обладающем внутренними точками множестве элементов ж С Еп, удовлетворяющих условиям вида fi(ж,u) 6 0,     г = [1,т] ,                                    (2)

где и Е Ө С Е^г - вектор параметров модели. Далее мы будем считать, что функции F k ( ж,и ) и f i ( ж,u ) имеют непрерывные частные производные требуемого порядка по всем своим аргументам.

Очевидно, что некоторую полезную информацию может дать последовательное решение следующих однокритериальных задач поиска, экстремума, на. множестве (2) каждой из функций (1) в отдельности для к = [1, N]:

F k (ж, и ) ^ max

X при условиях                                        (3)

f i ( ж,u ) 6 0,      г = [1,т] ,

с решениями ж**

К настоящему времени предложены многочисленные методы (см. [1], [2]), позволяющие, используя данные такого вида, получать различного рода маргинальные оценки количественных характеристик многокритериальных моделей.

При практическом использовании многокритериальных математических моделей достаточно часто набор независимых целевых функций заменяют некоторым дополнительным критерием, переходя таким образом к задаче математического программирования со скалярной целевой функцией, позволяющей находить, например, на множестве Парето согласованные или компромиссные в определенном смысле решения.

Ниже будет рассмотрен вариант подхода, в котором компромиссной является задача поиска на множестве (2) элемента, минимизирующего величину рассогласования целевых функций (то есть, максимального по всей совокупности критериев, отклонения каждого из критериев от своего неулучшаемого «идеала»).

Постановка задачи

Формально рассматривается задача математического программирования следующего вида:

минимизировать р, при условиях р > 0, fi(x, и) 6 0,

г = [1,ш] ,

Fk(ж,и) > F** - р, к = [1,V] , решение которой мы будем обозначать как р** (и) и ж** (и). Здесь F** = F (ж**, и).

Задача (4) может рассматриваться как параметрическая задача второго (верхнего) уровня, поскольку в формулировке ее условия содержатся F** к = [1, V] - решения однокритериальных задач(З), называемые задачами первого (нимснего) уровня. При этом как в задачах первого, так и второго уровня вектор параметров и Е Ө предполагается фиксированным.

Экстремальная величина рассогласования критериев rho определяется свойствами множества Парето и является для этого множества некоторой количественной характеристикой, зависящей от вектора параметров и. При этом для модели (1) - (2) естественно возникает оптимизационная задача третьего уровня, например такая:

оптимизировать по и Е Ө выражение р**(и),

решением которой будут являться вектор параметров и*** Е Эи чиело р*** = р**** .

Целью настоящей статьи является описание и обоснование некоторого подхода к решению задачи (5).

Метод решения

Решаем задачи отыскания в пространстве параметров стандартным (например, градиентным) методом поиска экстремума величины рассогласованности значений целевых функций многокритериальной модели (3) - (4) - (5).

Отметим, что особенностью этого подхода является тот факт, что постановка задачи (5) верхнего (третьего) уровня включает р*** - зависимость, являющуюся решением задачи (4) второго уровня, условие которой в свою очередь содержит зависимости F*_u = F_k (x*_u (и), и) Vk Е [1, V], определяемые решениями задач (3) нижнего (первого) уровня.

При этом зависимости р*** и Fk* Vk Е [1, V] в общем случае (даже для гладких функций Fk(x, и) и fi(x, и) ) не являются дифференцируемыми функциями, то есть непосредственное использование каких-либо численных методов, основанных на применении тейлоровских аппроксимаций, оказывается невозможным.

Для преодоления этого затруднения предлагается воспользоваться сглаживающим свойством метода функций обратных связей, описанного в [1], и аналогичного рассмотренному в [2], чтобы получить гладкие аппроксимации зависимостей p**(u) и F^u ) Vk Е [1,2V] , допускающие использование аппроксимаций по формуле Тейлора до второго порядка включительно.

При этом будем предполагать, что используемые в методе обратных связей функции удовлетворяют следующим условиям:

1°. Функция Р ( t,s) им еет Vt > 0 и Vs непрерывные производные по всем своим аргументам до второго порядка включительно.

2°. Для всех т > 0 и Vs выполнены неравенства д 2 Р ds2 >0 ■

ЭР

> 0; дs

3°. Р(т, s) > 0 Vs и любого т > 0, причем, кроме того, lim Р(т,5) = (+~, s> 0 ,(7)

-^+0 v 7     [     0, s < 0.

Использование метода функций сводится к следующему. Пусть

m

L„(х,A,u) = F„(x,u) — У^ Aifi(x,u)(8)

і =1

(дР.....)■

- стандартная функция Лагранжа для задачи (3), а функция

Q ( t, s) = inv

дР то есть обратна к —— . Тогда, исходя их оценочных соотношений, имеющих место при ds использовании метода гладких штрафных функций [3] для решения задачи (1) - (2) свя зывающих прямые и двойственные переменные (множители Лагранжа):

дР

Акиі = 1im ж~(т,.МХк(т,и))) Vi = [1,rn], т ^+0 дs \             / где Хк(т, u) - решение задач (3), полученное методом гладких штрафных функций. Можно построить систему уравнений

—— (хк, Лк) = -Q(t, Aki)    Vi = [1,ш] , дАкі

дL _k

^(х к , ^Л к ) =      ^Q(т,C kj )      ^vj = ^[1,n] .

^д^ к j                            ^J

В [4] показано, что в условиях (б)-(7) эта система всегда совместна и из нее одновременно находятся вектор-функции Х_к ( т,и ) и Лк(т, u) с компонентами { ^j (т, u) Vj = [1,n] } и { А кі ( т, u) Vi = [1,rn] } и которые в свою очередь можно использовать как приближенные оценки оптимальных значений прямых x „_u и двойственньix переменных Л к_и в задачах (3), когда последние имеют решение.

Несложно убедиться, что система уравнений (9) является условием стационарности вспомогательной функции пm

и(т, х, Л) = L(x, Л) - ^ R(t, ез) + ^ R(t, Ai),(10)

j=i в которой неотрицательная функция R(t, s) удовлетворяет соотношению Q(t, s) = —— .

Поскольку к системе (9) применима стандартная теорема о неявных функциях, то для вектор-функций { £ _kj (т, и ) V j = [1,п] } и { Х k_і ( т,и) Vi = [1,m] } будут справедливы следующие утверждения, как показано в [3].

На седловых траекториях для задач, имеющих ограниченные оптимальные значения целевых функций, существуют конечные пределы lim х(т) и lim Л(т), для которых т ^+0        т > ■ 0

lim_Q и(т,х ( т ) , Л( т )} = F ( х* = G (Л*) ,

а в случае единственности решений (регулярности) пары задач (1) и (2) справедливы также равенства lim х(т) = х* и lim Л(т) = Л* .                         (12)

т >  ■ 0                              т >  ■ 0

Рассмотрим теперь аналогичную схему решения задачи второго уровня (4), то есть получим асимптотические оценки решений этой задачи методом функций обратной связи.

Рассмотрим вначале схему решения задач первого уровня.

Будем использовать для однокритериальных задач (3) вспомогательную функцию вида

m

Uk(т,х, Л, и) = Fk(х,и) - ^ Хі/і(х,и)+ RR(т,х, Л) Vk Е [1,^],(13)

і=1

в то время как функции RR(т, s) в регуляризирующем слагаемом mm

RR(т, х, Л) = - ^ R(т, <3) + ^ R(т, Хг) з=1

по-прежнему выбираются согласно условиям (6) - (7).

В качестве сглаженной аппроксимации х* k ~ точного решения каждой из задач нижнего уровня (3), можно принять { х ^к (т, и), Л^k(т, и) } - стационарную точку вспомогательной

функции (13), определяемую, согласно теореме ний

о неявных функциях [5] системой уравне-

9U k 9^ j(k) dU k

. ^ӘХ з(к)

Vj Е [1,п] ,

Vi Е [1, m] .

или, что то же самое,

ЫС ^ k ^^х(к) , ^Л (k) ^

ЭБ к ^дХ г(к) dL k

. ^Э < з(К)

'^(х ( k ) , ^Л ( k ) )

'^(х ( k ) , ^Л (k) )

-

Q^{(т, Х} і(k) )

Q ( т,ё ₃(k) )

Vi = [1, m ] ,

Vj = [1,п] ,

- стандартная функция Лагранжа для задачи (3), а Q ( т, s ) =

dR ds

В рассматриваемой задаче в условие задачи второго уровня (4) входят зависимости F* k = F k ( х* _uk ,и ) Vk Е [1,^], не являющиеся дифференцируемыми функциями своих аргументов, то для этих зависимостей необходимо построить сглаженную аппроксимацию.

В качестве такой аппроксимации используем вспомогательную функцию, вычисленную в стационарной точке, то есть функцию F k ( и ) = U k ( т,х (k) ( т,и ) , Л^ ) (т, и ) , и ) , так как (в силу свойств метода штрафных функций) ее значение при малых положительных т близко к оптимальному значению целевой функции k-й задачи (3).

Стандартные методы оптимизации, используемые для задач нижнего уровня, основанные на использовании значений, градиентов или иных дифференциальных характеристик, предполагают, что помимо решения системы (14) можно находить и сами эти характеристики. Рассмотрим вначале процедуру вычисления производных функции Ғк(и) по компо нентам вектора параметров и, предполагая, что система (14) (или (15)) уже решена.

Поскольку Ғ к (и) = U _k (г, х^к ( т, и), Л^к( т, и ) , и^ ной функции имеем

, то по правилу дифференцирования слож-

(Ғ к^

х / *р

эи _к   ” эи _к -Р   А эи _к эх_{3        Г1} .

ди р +     д^ з ^дп р ⁺     дХ і ди р      ^{Р 6} [ , ^ '

Что в силу (14) дает

(^Ғ к ^ ^ р = ^ (^{т,жк (т,и) л (т,и),и})

Vp 6 [1, г] .

Отметим, что последнее упрощение было бы невозможным, если для Ғ *_к вместо сглаживающей аппроксимации и к ( т,Х ^к ( т,и ) , Л^к ( т,и ) ,и ) использовать аппроксимацию Ғ к ( Ж к ( т, и ) , и ) .

Рассмотрим теперь процедуру решения задачи второго уровня (4) методом функций обратных связей.

Построим для задачи (4) вспомогательную и-функцию, введя вектор М 6 Е ^N , - множителей Лагранжа для второй группы ограничений в задаче (4), для которого II^м II = II Р1, Р 2 ,... P N ||T :

Nm и (т, р, х, Л,М,и) = -р - ^Рк Үк (р,х,и) -’<^Хі/і(х,и)-к=1

п          Nm

-К(т, р) - £ К(т, ез) + £ К(т, Рк) + £ К(т, Хі),(17)

3=1            к=1

заменив предварительно в Ү к ( р,х,и ) зависимость Ғ *к на ее сглаженную аппроксимацию Ғ к ( и ) .

Условия стационарности вспомогательной функции (17) по совокупности переменных

}

| р, Х 1 , Х 2 , ... Х п , Х 1 , Х 2 , ... X m , Р 1 , Р 2 , . .. P N

будут	{ ди        N = —1 + ^ р к — Q(т, Р ) = 0 , др         к=1 ди N    дҒ к   m   д/ і                     r ,
	= ^ Рк^Т - Ехі^ -Q(т,^ 3 )=0    V3 6 [1,^] , д^ 3   к=1    д^ 3   і=1 д^ 3                                                (18) ди                     ...... дх = -/ і (х,и) + Q(т, ^ з ) = 0     Vi 6 [1, m] , ди — = -Ү к ( х,и ) + Q ( т,р к ) = 0     Vk 6 [1,^] . 1 др к

Обозначим решения системы (18) как р ( т, и ) , х ( т,и ) , Л( т,и ) , и М (т, и), тогда в качестве сглаженной аппроксимации зависимости р** можно использовать функцию

и ( т, и ) = и^т, р ( т, и ) , х ( т, и ) , Л( т, и ) ,М ( т, и ) , и^ .

Найдем производные этой функции по компонентам вектора параметров и.

По правилу дифференцирования сложной функции многих переменных имеем

ЭИ _ dU dU др A dU д^ Д дU дХг Л дU дрк дир  дир + др дир +   d^j дир + ^ дХг дир + ^ дрк дир ^ € ’ дU „ ди что. с учетом — = 0, — = ° V3 € [1,п], дает более простое выражение:

дU _ г , дU

= 0 Vг € [1,т] л -— = 0 Vk € [1,^] дХ г                     др к

дир = i ^U ^ ^t-^{=p ( t}.^u). - ^{( t}.^u).

Л( т,и ) ,М ( т,и ) ,и^ Vp € [1,г].            (19)

Наконец, получим формулы для компонент градиента от U ( т, и ) в терминах функций, используемых в формулировке многокритериальной модели (1) - (2) и методе функций обратных связей.

дu N дҮк  m   ә^           дҮк  дғ к  дік у— = - Д Рк я--Д Хі -— , причем для — = ---— дир к=1 дир  г=1  дир             дир   дир   дир

значения

дҒ _к                              _

—— определяются равенствами Ү к ( р,х,и ) = Ғ к (и) ди _р

- Р - Ғ к ( х,и )

Vk = [1,^].

Формулы (19) позволяют решать задачу верхнего уровня, применяя какой-либо из методов первого порядка.

Рассмотрим теперь метод нахождения для функции U (и) элементов матрицы Гессе, знание которой позволяет использовать в процессе поиска стационарных точек методы второго порядка.

Применяя к этой функции правила дифференцирования сложной функции, получаем

′′

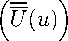
U p H q

д 2U     д 2U др Д  д 2U д^j дирдич дирдр дир 2-у^ дирд^j дир

m

+Д

і=1

д 2U дХг   Д д2U дрк дирдХг дир      дирдрк дир

Vp,q = [1,т].

Вторые частные производные вычисляются непосредственно вые производные, т.е.   ——, —— V3 € [1,п], —- Vг € др д^              дХг

в точке | х,

[1,ш] II

р, Л, м| , а пср-дU „ _{г п} — Vk € [1,^] др к

могут быть найдены по теореме о неявных функциях [5] из системы линейных уравнений:

Э2U др   п Э2U ЭЕ +          >у Эр2 Эиу j=1 Эрд^з Эиу + m Э2U ЭХі W' Э2U Эрк Э2U + V-- і=1 ЭрЭХі Эиу + к=1 ЭрЭ^к Эид ЭрЭид , Э2U Эр   п Э2U ЭЕ Э^һЭр Эич ' 3=1 Э^ Эич + m Э 2U ЭХі ,N Э2U Эрк Э2U ⎪ + і=1 Э^һЭХі Эич + к=1 Э£һЭ^к Эич Э^һЭиу , Э 2U Эр   «  Э 2U ЭЕ (20) ---Һ V--- ЭХ8Эр Эи 1 з=1 ЭХ8Э^з Эиу + m Э2U ЭХі £ Э 2U Эрк Э 2U + і=1 ЭХ.ЭХі Эич + к=1 ЭХ8ЭЦк Эид ЭХ8Эид , Э2U Эр л Э2U Э^і --щ + у--Е + ЭptЭр Эич j=i ЭptЭ^з Эич m Э 2U ЭХі £ Э2U Эрк Э2U + і=і ЭptЭХі Эич + к=і ЭptЭpк Эич Эpt Эиу ’ которая в свою очередь получается при последовательном дифференцировании по переменным р и Xj j = [1,n] условий стационарности (18). Заметим, что в формулах (20) мы используем Һ = [1, n] , s = [1, m] , t = [1, N] .

В этом случае приближенное решение задачи верхнего уровня сводится к поиску экстре мума по и вспомогательной функции

U(т,и) = и^т, х(т, и), Х(т, и), и) , для реализации

которого также можно использовать стандартные итерационные алгоритмы.

Например, для методе Ньютона компоненты улучшающего вектора w находятся из системы линейных уравнений

п

^ ^U‘^_р w = ^-U \ .    Vp = ^[1 Д^] .

t=i

Наконец заметим, что при необходимости и соответствующих предположениях о гладкости функций (1) - (2), из линейных систем с той же основной матрицей могут быть найдены значения производных более высокого порядка.

Пример решения задачи

Проиллюстрируем особенности такой постановки задачи следующим примером.

Рассмотрим достаточно наглядную многокритериальную математическую модель, в которой х = || ^і^2^з|^т Е Е 3 - вектор независимых переменных, а вектор параметров и = || U i U 2 | ^T Е Е² .

Требуется максимизировать по х при некотором и С Ө Е Е² функции

Ғ 1 ( х,и) = х 1 , Ғ 2 ( х,и ) = и 1 х ₂ , Ғ з ( х,и ) = 3 х з                   (21)

при условиях: х 1 >  0 , х ₂ >  0 и хз >  0 ,

/1 (х, и) = хі + х2 + хз 6 U2 , где Ө : | 0 6 и1 6 6; 0 6 и2 6 10 } .

Для решения используем, примененную в [4], функцию обратной связи вида

=1 (' -1)

QC^s)

. Тогда система (15) (например, для к = 2) будет

^-« 2 + Жф) + ⁵ 2(2) + ⁵ з(2)

^A (2)

^-n 1 ⁺ Л (2)

^A (2)

= т(Х(2)- І)’ = "1 (51(2) - $У ’ = -1 (52(2) - 5^) ’ = -1 (5з(2) - У ■

Решая предварительно задачи нижнего уровня, то есть системы (15), которые в приводимом примере имеют вид (22), находим F 1 , F 2 и F 3 - значения сглаженных оценок целевых функций одноэкстремальных задач F *_k = F ;, (ж*^, n) Vk G [1,^].

Затем, используя эти оценки, формируем условие задачи второго уровня - системы (18), которая для данной задачи имеет вид

-« 2 + 5 1 + 5 2 + 5 з

F 1 - 5 1 - р

F 2 - « 1 5 2 - р

F з - 35 з - р

^A 1 ^- p i

^А 1 ^- « 1 ф

A i ^{- 3р} з

1 ^p . ^{- р} 2    ^р з

1(A-I)

-1 (Р1 - й

-1 (Р2 - Р1;)

-1 (Рз - Р1з)

- ^5 1 -

2 у Х 1

-1 (52 - е)

-1 (5з - 51з)

(р

-

Решение системы (23) для точки в пространстве параметров с П1 = 2 11 «2 = 5 при

различных значениях т приведено в табл. 1.

Таблица 1

т	Х 1	Ж 2	Ж3	Р	А	Д1	Л2	Лз
10-1	0.036183480	1.942605273	3.056791852	6.150359244	1.417219233	0.037182321	0.744305433	0.517900602
10-2	4.116 • 10-3	1.992735259	3.005146639	6.024189515	1.219555846	4.813 • 10-3	0.613505204	0.410972589
10-3	4.162 • 10-4	1.999258339	3.000510447	6.002509934	1.201920729	4.980 • 10-4	0.601335133	0.401084782
10-4	4.166 • 10-5	1.999925683	3.000051004	6.000251899	1.200191707	4.998 • 10-5	0.600133351	0.400108348
10-5	4.167 • 10-6	1.999992567	3.000005100	6.000025199	1.200019167	5.000 • 10-6	0.600013334	0.400010833
10-6	4.167 • 10-7	1.999999257	3.000000510	6.000002520	1.200001917	5.000 • 10-7	0.600001333	0.400001083
10-7	4.167 • 10-8	1.999999926	3.000000051	6.000000252	1.200000192	5.000 • 10-8	0.600000133	0.400000108
10-8	4.167 • 10-9	1.999999993	3.000000005	6.000000025	1.200000019	5.000 • 10-9	0.600000013	0.400000011

Заметим, что точное решение задачи второго уровня при значениях параметров U1 = 2 и П2 = 5 имеет вид жД = 0; ^* = 2; ж3* =3; р** = 6; А** = 1.2; рД =0; р2* =0.6; р** = 0.4.

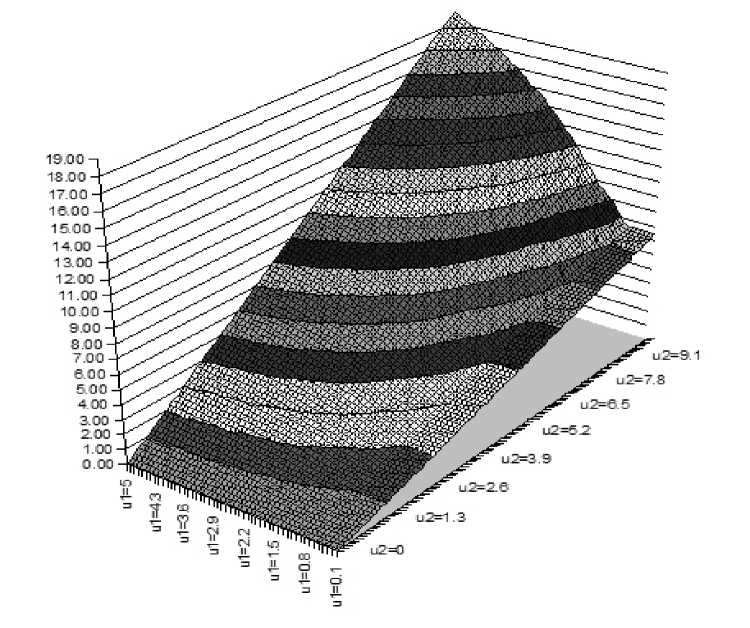
Рис. 1. Графическое представление зависимости р ( т, и )

Графическое представление зависимости р(т, и) показано на рис. 1. Для решения задач типа (17) в рассматриваем примере можно использовать любую стандартную градиентную схему, описанную, например, в [6].