Гладкие модели биологических популяций

В данной работе строятся модели, выражающие численность биологических популяций, на. основе анализа, временных рядов [1 -6].

Особенность временных рядов в экологии состоит в том, что, во-первых, для исследования доступно незначительное число значений, поскольку, как правило, представленные эмпирические данные - это результаты измерений в течение 30 - 50 лет. Во-вторых - малая точность, потому как практически невероятно измерить численность всей популяции, вплоть до отдельной особи, на. большом ареале ее обитания. В-третьих - реакция биосферы и ее объектов на. внешние воздействия носит избирательный характер, т.е. объекты биосферы не реагирует на. все воздействия одновременно, при этом один и тот же объект биосферы в разные интервалы времени может реагировать на. одинаковые воздействия по-разному, характер и сила, наблюдаемой реакции могут не соответствовать параметрам внешних воздействий. Отсюда. - возникновение сложностей при построении вида, модели.

В связи с вышеизложенным, прежде чем приступить к моделированию по временному ряду, строится сглаженный набор эмпирических данных, который отражает лишь общие черты реального временного ряда. Это достигается посредством построения оптимизационного сплайна: весь временной интервал, в пределах которого лежат измерения наблюдаемой величины, делится на. несколько равных промежутков, на. каждом промежутке строится свой полином заданной степени, исходя из следующих условий: на. границах временных интервалов значения соседних полиномов, а. также их последовательных производных до некоторого фиксированного порядка, должны совпадать. Более того, кусочный сплайн, составленный из этих полиномов, должен быть экстремальным в своем классе, исходя из условия оптимального отклонения от эмпирических данных на. всем временном промежутке по методу наименьших квадратов. Далее, к сглаженному временному ряду применяется аналог метода. Безручко - Смирнова. [7], заключающегося в построении системы дифференциальных уравнений, решение задачи Коши для которой моделирует зависимость, выражаемую данным временным рядом.

Е.В. Лобанова, Н.Б. Медведева

В данной статье описанные методы применяются к конкретным временным рядам, выражающим численность биологических популяций, вычисляется погрешность прогноза, исследуется зависимость погрешности от некоторых параметров метода. Кроме того, метод применяется к искусственному временному ряду, содержащему случайные возмущения, исследуется зависимость погрешности прогноза от величины возмущения.

1.    Сглаживание эмпирических данных

Перечислим основные элементы процедуры построения оптимизационного сплайна. Пусть задан скалярный временной ряд { v i } MQ , задающий последовательность значений размера популяции на протяжении определенного количества лет, t i = i (i = 0,..., M) -временная сетка, M - натуральное число. Предположим, что M = lk, где l >  1,k >  1 -натуральные числа. Тем самым весь временной интервал I = [0, M], в пределах которого лежат измерения наблюдаемой величины, делится на к равных промежутков I = U k=i I i , на каждом из которых доступны, следовательно, l + 1 значений. По этим значениям строятся полиномы y _ni (t) = П=0 сО c ij • t ^j заданной степени n, исходя из следующих соображений: в каждой граничной точке t _{i · l} промежутков I i соседние полиномы должны принимать одинаковые значения вместе со всеми своими производными до заданного порядка d:

Mt i ^ i ) = ^Aki), ^tkt i ^ i ) = ^(k i ), ..., ^a id ^(t i ^ i ) = ^H-ifei ), i = ^1,...^,k ^{- 1}

Кусочный сплайн a n (t), составленный из функций a _ni (t),. .. ,a nk (t):

^ n (t) = <

^ nl (t), ^ n2 (t),

t G I l , t G I 2 ,

, ^nk(t),     t G Ik, должен быть экстремальным в своем классе, исходя из условия оптимального отклонения сплайна от эмпирических данных и его производных от нуля на всем временном промежутке:

M        dM

^ (^ n (t i ) ^{- v} i ^{) 2} + ££ (^ ⁽ t i ^{)) 2} ^ ^min . i=0                   s=1 i=0

Такой способ построения позволяет однозначно определить все коэффициенты c _Io ,...,C kn оптимизационного сплайна.

2.    Реконструкция систем дифференциальных уравнений

Метод моделирования по временным рядам с помощью построения системы обыкновенных дифференциальных уравнений, разработанный Безручко – Смирновым [7], состоит в следующем. В случае, если исходный временной ряд – векторный размерности D, то вычисляются разностные производные первого порядка компонент этого ряда. Модель строится в виде задачи Коши для системы дифференциальных уравнений

ЗС i (t) = F i (x i ,X 2 , ...,X D ),

ЭС 2 (t) = F 2 (x i ,X 2 , ...,X D ),

_ X D (t) = Fd (xi,X2,...,XD ), в которой Fj, j = 1... D - многочлены некоторой фиксированной степени K с неопределенными коэффициентами, которые ищутся из условия минимального отклонения разностных

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ производных компонент временного ряда от соответствующих компонент правой части системы (2) по методу наименьших квадратов.

В случае же, если исходный временной ряд – скалярный, модель строится в виде задачи Коши для системы обыкновенных дифференциальных уравнений некоторой размерности D > 1

x I = X2, x 2 = x3,

< x 3 = x 4 ,                                                      (3)

...,

, xD = F(xi, . . . ,XD), где F(xi,..., xd) — многочлен степени K, коэффициенты которого ищутся методом наименьших квадратов из условия минимального отклонения разностной производной временного ряда порядка D от значений многочлена F на наборе разностных производных временного ряда до порядка D — 1 включительно. Вопрос о выборе размерности D требует специального обсуждения.

Метод Безручко – Смирнова показал свою эффективность при моделировании временных рядов, возникающих при измерениях в технических устройствах, содержащих сотни и даже тысячи измерений.

• 3.    Схема построения модели

Первый этап построения модели популяции по временному ряду – это нахождение оптимизационного сплайна, который может быть как векторным, так и скалярным. Далее применяется аналог метода Безручко – Смирнова к дисретизированному сплайну, для чего временной промежуток делится на большое количество частей N – порядка сотен или даже тысяч, таким образом получается новый сглаженный временной ряд, производные которого в точках сетки вычисляются в отличие от метода Безручко-Смирнова аналитическим дифференцированием оптимизационного сплайна в системе MAPLE.

Если временной ряд – векторный размерности D , то модель ищется в виде задачи Коши для системы (2), где

K   DD

F(xi,x2,...,xD) =    ^2    cj,ii,i2,...,iDnxkk, 52 ^-K, l1 ,l2,...,lD =0                k=1          k=1

– полиномы степени не выше K , коэффициенты которых ищутся для каждого j из условия минимума

N

^ ⁽ F j ^{( ст} П ^(h • iV-^D ⁽h • i)) ^{— (} ^ n ) ‘ ⁽ h • i ^{)) 2} ^ min, i =0

где ст П - оптимизационный сплайн для j -й компоненты временного ряда, h = M/N .

Когда наблюдению доступен лишь скалярный временной ряд, процедура построения системы (3) включает в себя еще один предварительный этап (по сравнению с моделированием по векторному ряду) – выбор размерности модели D , который в простейшем случае можно осуществить на основе перебора. В данной статье мы исследуем зависимость погрешности прогноза от величины D . Модель в этом случае ищется в виде задачи Коши для системы (3), где

KDD

F(xi,x2, ...,xd)=    ^2    cii,i2,...,iD IJxk , 52 lfc - K,(4)

l1 ,l2,...,lD =0              k=1

Е.В. Лобанова, Н.Б. Медведева

– многочлен степени K , коэффициенты которого находятся из условия минимума

N

^ (F (ст _п (Н • i), ст П (h • i),..., a D ¹ (h • i)) - ^(h • i)) ² ^ min . i=0

Качество построенной модели исследуется с точки зрения адекватности прогноза. Промежуток определения временного ряда делится на две части – тренировочную и тестовую: M = M train + M test . Для исследования погрешности прогноза оптимизационный сплайн строится не на всем промежутке I = [0, M], а на промежутке [0, M train ], далее на этом же промежутке строится система дифференциальных уравнений (2) или (3). Далее ищется численное решение задачи Коши для этой системы дифференциальных уравнений на всем промежутке I = [0, M]. Численное решение сравнивается с исходными эмпирическими данными на тестовом промежутке [M train , M ]. Ошибка прогноза в случае скалярного временного ряда вычисляется по формуле

Е = max      | x i (t i ) - V i | ,

t i G [M train ,M ]

а в случае векторного – по аналогичной формуле для каждой компоненты.

Программа построения оптимизационного сплайна, модельной системы дифференциальных уравнений, решения соответствующей задачи Коши, построения графиков и вычисления погрешности прогноза была реализована в системе MAPLE 14.

4.    Реализация метода в случае одновидовой популяции

Приведем ряд демонстрационных примеров реализации вышеизложенного метода с использованием математического пакета Maple 14. В качестве одновидовой системы была выбрана популяция цапли Ardea cineria на юге Ланкашира, Англия, с указанными в табл. 1 показателями на протяжении 30 лет [8].

Показатели численности популяции цапли

Таблица 1

Год	1912	1913	1914	1915	1916	1917	1918	1919	1920	1921
Число пар	20	21	22	25	29	34	37	38	37	37
Год	1922	1923	1924	1925	1926	1927	1928	1929	1930	1931
Число пар	37	40	43	45	46	46	46	47	49	51
Год	1932	1933	1934	1935	1936	1937	1938	1939	1940	1941
Число пар	52	52	51	52	53	55	56	57	57	58

На основании приведенных данных был построен оптимизационный сплайн, сглаживающий эмпирические данные, на обучающем промежутке длины M train = 22 года. В качестве степеней полиномов, образующих данный сплайн, была выбрана степень n = 9, уровень гладкости сплайна d = 3. Весь обучающий временной интервал был разделен на к = 7 равных частей по l +1 =4 измерения в каждом. График полученного сплайна og(t) изображен

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

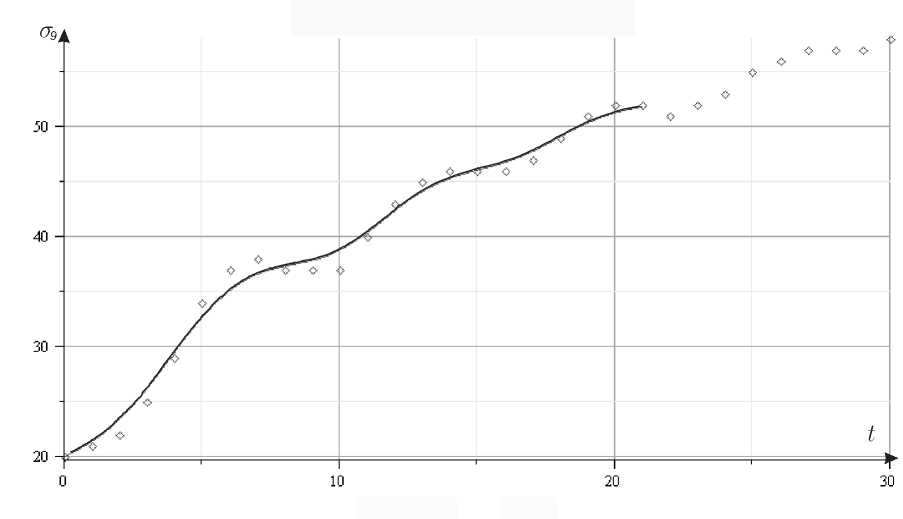
Рис. 1 . График оптимизационного сплайна a(t) для популяции цапли Ardea cineria

на юге Ланкашира, Англия, 1912 – 1941 гг.

на рис. 1. Затем выбранный промежуток был разбит на N = 300 частей, и полученные значения легли в основу нахождения методом наименьших квадратов коэффициентов системы вида (3) размерности D = 3 со степенью полинома (4) в правой части, равной K = 2:

Х 1 = Х 2 ,

< Х 2 = Х3,                                                        (6)

, Х3 = F(Х1,Х2,Хз), где F(Х1, Х2, Хз) = Со + С1Х1 + С2Х2 + С3Х1Х2 + С4Х1 + С5Х2 + С6Х1Х3 + С7Х2Х3 + С8Х2.

После того, как все коэффициенты c 0 , ..., c 8 были найдены из условия:

^ ⁽ F ⁽ СТ 9 ⁽ h • i) ,^ 9 ^{( h} • i), a % ^{( M} • i)) — CTg ‘ ^{( M} • i ^{)) 2} ^ min, i=0

где h = M/N = 0,1, численным методом было получено решение системы (6) с начальными условиями Х 1 (0) = 20, Х 2 (0) = ст 9 (0), Х з (0) = ст 9 ‘ (0). Функция x i (t), является на тестовом промежутке прогнозом численности популяции английской цапли (рис. 2). Подсчитано, что в данном случае погрешность прогноза ε, вычисленная по формуле (5) не превышает двух особей.

Как можно увидеть из рис. 2 графики оптимизационного сплайна и найденного решения системы (6) практически совпадают на тренировочном промежутке, а график прогноза визуально хорошо совпадает со значениями исходной выборки на тестовом промежутке.

Для указанных выше начальных данных и значений n, d, l и D была исследована зависимость погрешности прогноза от частоты разбиения на N отрезков, по которым осуществлялось нахождение коэффициентов в условии (7). Из полученных данных (рис. 3) можно сделать вывод, что стабильное уменьшение ошибки прогноза и, следовательно, увеличение его точности достигается уже при значениях N > 500.

Е.В. Лобанова, Н.Б. Медведева

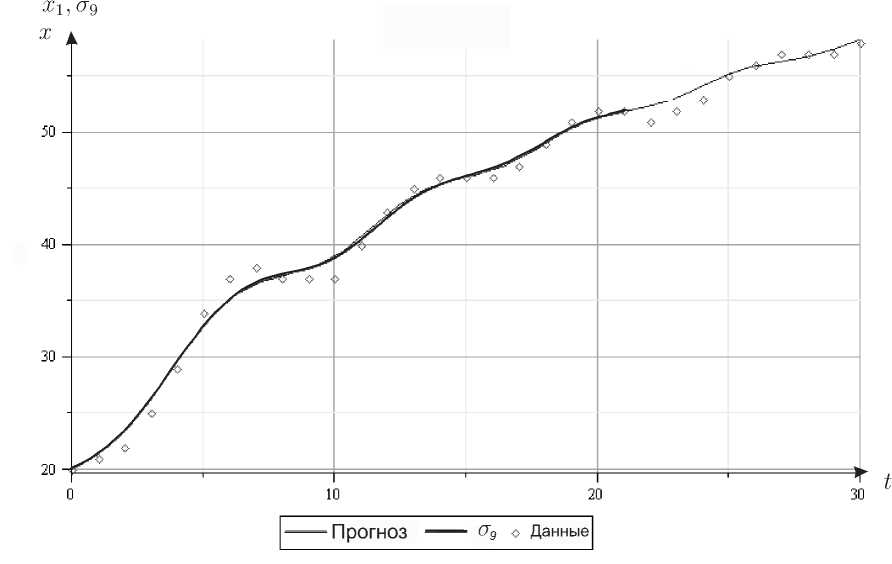
Рис. 2 . Прогноз численности популяции цапли Ardea cineria на юге Ланкашира, Англия, 1912 – 1941 гг.

Как показали также аналогичные исследования для двухвидовой популяции, существуют небольшие значения N , при которых достоверность прогноза достаточно велика (здесь это достигается, к примеру, при N = 100, N = 275, N = 400).

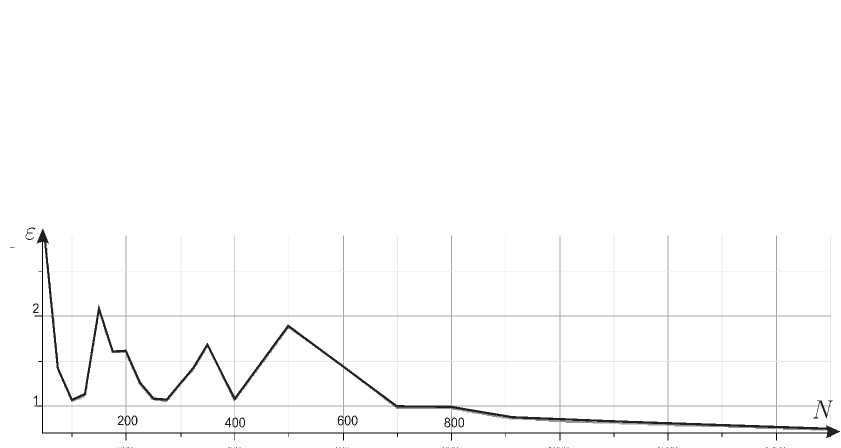
Рис. 3 . Зависимость погрешности прогноза от частоты разбиения N для численности цапли Ardea cineria на юге Ланкашира, Англия, 1912 – 1941 гг.

Наконец, реализация метода для различных размерностей D системы вида (3) при n = 9, d = 3, l + 1 = 4, N = 300 привела к следующему результату: самой оптимальной в плане

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ точности прогноза стала размерность D = 3, что соответствует теоретическим результатам Такенса о вложениях [9].

Проведенные эксперименты со степенью полиномов n, составляющих оптимизационный сплайн a n (t) и построенных при наличии l + 1=2 измерений на одном отрезке разбиения всего временного промежутка, показали, что с ростом степени n растет точность прогноза численности исследуемой популяции.

5.    Исследование метода с помощью искусственной выборки

X, Xb (7g

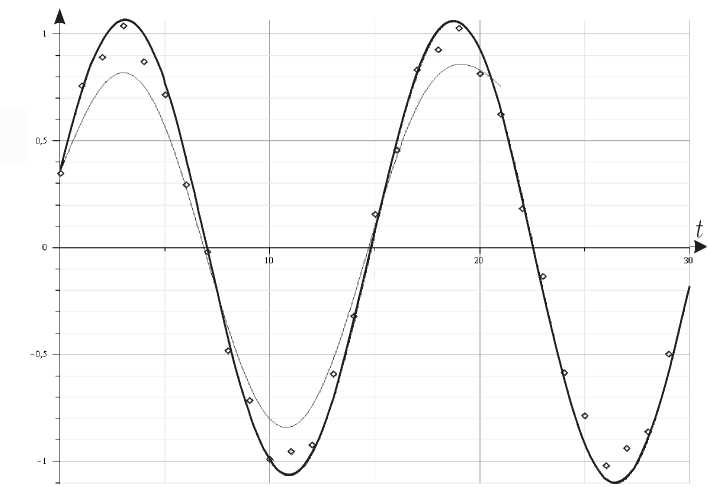
Рис. 4 . График сплайна a ₉ (t) изображен тонкой линией, жирной линией изображено решение системы (6) - прогноз для искусственного временного ряда x(t) = sin(0,4 • t) с уровнем шума, не превосходящим 4%

Для исследования зависимости точности прогноза от величины вводимых шумов мы рассмотрели искусственный временной ряд, получаемый из функции x(t) = sin(0,4 • t) путем добавления случайных добавок величины 6 на целочисленной сетке t i = i, i = 0,..., 30, (ромбики на рисунке 4). Аналогично случаю одновидовой системы был построен сплайн на тренировочном промежутке [0, 22], затем система вида (6). Исследование влияния добавленных шумов в данную конструкцию выявило характерное снижение неточности прогноза при уменьшении уровня зашумленности временного ряда. Зависимость погрешности прогноза ε от шумов δ представлена на рис. 5.

6.    Применение метода к двухвидовой популяции

Были проведены эксперименты с данными о численности популяций рысей и зайцев [8], представленными в табл. 2. В качестве модели взаимодействия двух популяций мы рассмотрели задачу Коши для системы обыкновенных дифференциальных уравнений вида (2)

Е.В. Лобанова, Н.Б. Медведева

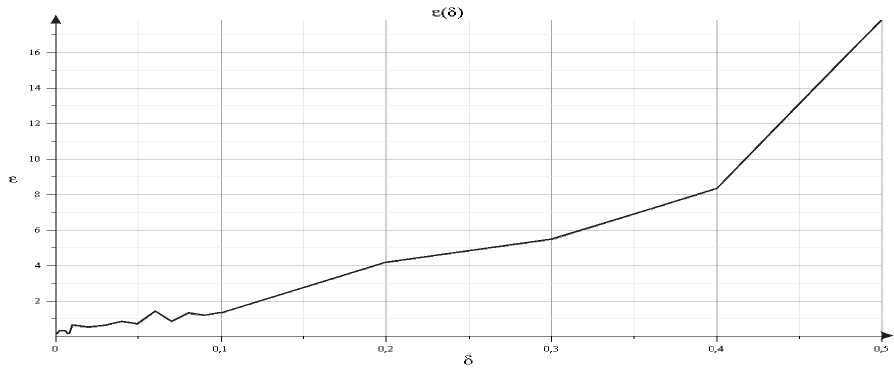
Рис. 5 . Зависимость погрешности прогноза е для искусственной системы x(t) = sin(0,4 • t) от уровня вводимого шума 5

Таблица 2

Год	1950	1951	1952	1953	1954	1955	1956	1957	1958	1959
Число пар рысей / зайцев	35/20	33/21	35/18	21/25	11/26	10/28	9/38	8/39	9/49	14/67
Год	1960	1961	1962	1963	1964	1965	1966	1967	1968	1969
Число пар рысей / зайцев	18/86	24/96	22/90	31/93	37/82	34/65	30/59	24/51	19/49	20/54
Год	1970	1971	1972	1973	1974	1975	1976	1977	1978	1979
Число пар рысей / зайцев	14/57	15/63	18/80	23/86	27/96	29/94	30/81	33/75	35/64	33/62

Показатели численностей популяций рысей и зайцев

размерности D = 2

( X 1 = F 1 (x i ,X 2 ),

( X 2 = F2(xi,X2), где Fi(xi,X2) и F2(xi,x2) — многочлены степени K = 3 от двух переменных:

^F j ^(x 1 , ^x 2 ) у c j,l 1 ,l‘ 2 ^x 1 ^x 2 , j ¹ , ² *

• l 1 +l 2 ≤ 3

Аналогично одномерному случаю мы взяли для каждой компоненты временного ряда степень полиномов, образующих оптимизационный сплайн, равной n = 9 с уровнем гладкости d = 3, разбиение обучающего временного интервала на равные части по l + 1 = 4 измерения в каждом. Для построения системы (8) тренировочный промежуток был разбит на N = 300 частей. Численно было построено решение системы (8) с начальными условиями С 1 (0) = 20, С 2 (0) = 35. Полученные результаты отражены на рис. 6.

Исследование зависимости погрешности прогноза от степени полиномов K в правой части (8) показало, что возрастание степени правой части K ведет, во-первых, к сильному росту времени счета, делая его иногда невозможным, а во-вторых, вообще говоря, не ведет

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

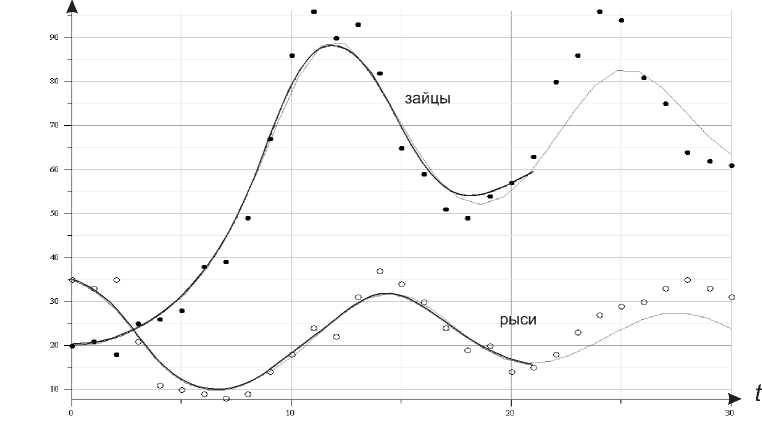
Рис. 6. Прогноз численности популяций рысей и зайцев. Оптимизационные сплайны обозначены толстыми линиями, прогнозы – тонкими линиями к увеличению точности прогноза. В обоих случаях наилучший результат был достигнут при K = 3. Исследование зависимости погрешности прогноза, рассчитанной по формуле (5), от степени оптимизирующего сплайна n и в этом случае показало, что, как правило, чем выше его степень, тем надежнее прогноз.

Работа проводилась при финансовой поддержке РФФИ, грант 13-01-00512.