Гомотопическая инвариантность возмущений квантовых дифференциальных модулей
Автор: Лапин Сергей Валерьевич
Журнал: Инженерные технологии и системы @vestnik-mrsu
Рубрика: Алгебра и геометрия
Статья в выпуске: 4, 2010 года.
Бесплатный доступ
В данной работе вводится понятие возмущения квантового дифференциального модуля и устанавливается свойство гомотопической инвариантности возмущений квантовых дифференциальных модулей.
Короткий адрес: https://sciup.org/14719593
IDR: 14719593
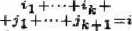
Список литературы Гомотопическая инвариантность возмущений квантовых дифференциальных модулей
- Лапин С. В. Дифференциальные возмущения и £>оо-дифференциальные модули/С. В. Ла-пин//Мат. сб. -2001. -Т. 192, Ш 11. -С. 55-76.
- Gugenheim V. К. А. М. On a chain complex of a fibration/V. К. А. М. Gugenheim//Illinois J. Math. -1972. -Vol. 3. -P. 398-414.
- Gugenheim V. К. A. M. Perturbation theory in differential homological algebra I/V. К. A. M. Gugenheim, L. A. Lambe//Illinois J. Math. -1989. -Vol. 33, № 4. -P. 566-582.
- Gugenheim V. К. A. M. Perturbation theory in differential homological algebra II/V. К. A. M. Gugenheim, L. A. Lambe, J. D. Stasheff//Illinois J. Math. -1991. -Vol. 35, N* 3. -P. 357-373.
Статья научная
