Градиентные теории упругости и способы идентификации градиентных параметров моделей

копию этой лицензии, перейдите по ссылке

Применение классической теории упругости при оценке напряженно-деформированного состояния некоторого тела ограничено определенным масштабным уровнем рассматриваемого тела (или его части). Обычно это связано с наличием значительных неоднородностей материальных характеристик, начиная с микроуровня и ниже. Для таких объектов необходимо использовать неклассические теории упругости, которые позволяют учитывать нелокальность деформаций. К таким теориям относятся градиентные теории упругости, основной особенностью которых является то, что они учитывают не только деформации, но и их пространственные производные, поэтому уравнения включают тензор моментных напряжений наряду с тензором Коши. Это значительно усложняет постановку и решение задач, получение их аналитических и численных решений.

Настоящая работа содержит обзор исследований по градиентным теориям упругости. В рамках обзора представлены и проанализированы работы, касающиеся как общей теории, так и различных приложений. Также изучены способы идентификации параметров неклассических моделей, что является нетривиальной проблемой в отличие от клас- сической теории упругости. На основе анализа авторами была решена задача одномерной деформации тяжелого тонкого слоя. На основе решения предложенной задачи был предложен оригинальный способ идентификации градиентного параметра.

Общая теория неклассических сред

Первоначальные идеи. В последнее время (начиная с 90-х годов прошлого века) в связи с появлением и разработкой новых материалов, а также благодаря тренду на миниатюризацию электронно-механических систем и их компонентов, активно развиваются теории обобщенного континуума, использующие неклассические определяющие соотношения [1]. Это связано, прежде всего, с необходимостью описания размерных эффектов, в том числе, в нано-структурированных материалах, различных сверхтонких структурах, материалах с большими градиентами неоднородностей, и другими задачами на мезо- и микроуровне [2].

Первоначальные идеи исходят от теории братьев Эжена и Франсуа Коссера [3, 4], называемой в настоящее время несимметричной теорией упругости (моментной теорией упругости). Особенности модели Коссера состоят в том, что для каждой частицы среды кроме вектора перемещений вводится еще одна кинематическая переменная – вектор поворота, в связи с чем, наряду с обычными напряжениями в среде возникают также моментные напряжения.

Дальнейшее развитие теории Коссера началось с классической работы К. Трусделла и его ученика Дж. Эриксена [5]. Современная трактовка континуальной модели, включающей эффекты второго порядка, дана в работе [6]. Позднее Р. Тупин получил аналогичные определяющие уравнения для конечных деформаций [7]. Далее эти идеи развивались в работах Р. Миндлина [8], Э. Аэро и Е. Кувшинского [9], В. Пальмова [10] и др.

Модели нелокальной упругости. Модели основаны на предположении, что силы между материальными точками могут иметь дальнодействующий характер, что отражает дальнодействующий характер межатомных взаимодействий. Э. Кренер дал физическое обоснование нелокальной теории на основе теории дислокаций [11,12]. А. Эринген и Д. Эделен получили определяющие уравнения нелокальной теории на основе вариационного подхода [13]. Физические основы нелокальной упругости обобщены в работе И. Кунина [14]. Вариационный подход к выводу достаточно общих уравнений нелокальной градиентной теории высокого порядка представлен в работе [15].

Развитие общей теории. Общие вопросы градиентной теории упругости рассматривались отечественными учеными. Так, С. Лурье и В. Васильев в работе [16] указывают на необходимость формулировки условий симметрии, аналогичным требованиям к тензору жесткости анизотропного тела в классической теории упругости. Это симметрия по перестановке индексов в первой и второй паре индексов, а также при перестановке этих пар. Последнее требование вытекает из условия существования потенциала упругой энергии. Авторы развивают подобные требования применительно к градиентным теориям упругости с целью получения корректных физических уравнений.

Вариационная формулировка градиентной анизотропной теории упругости представлена в работе [17]. Наряду с классическим тензором анизотропных модулей четвертого ранга предложено ввести вектор размерности длины.

Некоторые работы посвящены развитию градиентной теории при конечных деформациях. Например, показано, что условия эллиптичности уравнений градиентной теории упругости при конечных деформациях, когда плотность энергии деформации является функцией первого и второго градиента вектора градиента места, накладывает определенные ограничения на касательные модули [18].

Особенности неклассических моделей. Развиваемые модели позволяют учитывать масштабные эффекты, поскольку определяющие соотношения включают градиентные параметры, соотносимые с размерными параметрами исследуемой области, например, с размерами зерна (дефекта), толщиной покрытия и т.п. Модели позволяют получать регулярные решения в окрестности острых трещин (так называемых особых точек), более гладкие решения для многокомпонентных (зернистых) материалов с микро- и нановключениями, рассматривать адгезионные эффекты, масштабные эффекты и др.

Поскольку плотность энергии деформации в неклассических моделях зависит не только от тензора деформаций, но и от градиента деформации первого (второго и т.д.) порядка, это приводит к уравнениям более высокого порядка, чем в классической теории упругости. Данное обстоятельство усложняется требованием формулировки дополнительных граничных условий, а также определением множества дополнительных параметров модели. Все это является определенной "платой" за новые возможности градиентных теорий.

Упрощенные модели градиентной упругости. На практике используются, как правило, упрощенные (прикладные) градиентные модели с малым количеством параметров, в частности, однопараметрические модели, наиболее распространенной из которых является вариант Е. Айфантиса [19]. Другим вариантом упрощенной (одно- и двухпараметрической) модели является подход В. Васильева, С. Лурье [16, 20]. Этими же авторами в работе [21] представлена новая однопараметрическая модель обобщенной теории упругости. Рассмотрены постановки задач различной размерности.

Подобные модели и используются в основном в различных приложениях, например [22, 23]. Таким образом, максимально упрощенный вариант физических уравнений одномерной градиентной теории упругости (вариант Е. Айфантиса [19]) выглядит следующим образом:

a = Ee + LE^ ,

dx где E – модуль упругости; L – градиентный параметр, имеющий размерность длины.

Применение неклассических теорий упругости к решению различных задач

Задачи деформирования балок, пластин с концентраторами. К настоящему времени в рамках градиентной теории упругости решено достаточно много различных прикладных задач. Решение статических задач изгиба стержня представлены в работах [19, 23–25 и др.], а деформации цилиндра в работах [26, 27 и др.]. Задачи изгиба пластин, растяжения пластины с отверстием и подобных рассматривались в работах [28–29 и др.]. Авторами статьи [30] в рамках континуума Коссера проведен анализ аналитического решения задачи Кирша и показано отличие классического и неклассического решений.

Задачи теории трещин . Классическая линейная упругость приводит к бесконечно большим напряжениям в вершине острой трещины, а поскольку сингулярность напряжений не является реальной, то в этом случае классические критерии разрушения не применимы . Градиентная теория устраняет сингулярность напряжений, что приводит к определенным преимуществам описания [31].

Подробное применение моментной теории упругости к задачам трещинами изложено в монографии Н. Морозова [32]. Новый вид решения плоской задачи градиентной теории упругости при наличии острой трещины представлен в [33].

Задачи механики композиционных материалов, наноматериалов. Градиентные теории упругости применяются при анализе напряженного состояния в тонких покрытиях (слоях) в композиционных материалах. В частности, в работе [34] рассмотрены тонкие покрытия, применяемые в авиакосмической области. Модель материалов со сферическими анизотропными наночастицами представлена в работе [35]. Изгиб консольных нано-трубок с целью разработки резонаторов изучался в работе [36]. В работе [37] рассматривается модель композиционного материала, армированного двунаправленными волокнами, описывающая плавные переходы полей сдвиговых деформаций.

Динамические задачи. Применение градиентной теории упругости при описании различных динамических эффектов, в частности колебаний, приводит к различным эффектам. Так, многие авторы отмечают, что когда толщина микро-пластины сравнима с масштабным параметром модели, увеличивается собственная частота колебаний, например [38]. Аналогичный эффект наблюдается и для продольных колебаний нано-стержня [39].

Нелинейные продольные и сдвиговые волны деформации, распространяющиеся в градиентно-упругой среде, изучаются в работе [40]. Колебания полосы с отслоением в рамках однопараметрической модели Е. Айфантиса рассмотрены авторами работы [41], где получены смешанные полуаналитические решения для градиентной упругости.

Динамические задачи для микро- и нано-объектов часто возникают в связи с разработкой различных нано-электромеханических систем (датчиков), например [42]. В подобных задачах необходимо учитывать влияние нано-размерных эффектов, что было сделано в работе [43], где рассматривались колебания круглой ортотропной пластины с учетом эффектов градиентной упругости.

Градиентная теплопроводность и термоупругость. Значительная часть работ посвящена полусвязанным термоупругим задачам, когда температурное поле определяется по обычным классическим законам, а напряженно-деформированное состояние, индуцированное тепловыми эффектами – по градиентной теории упругости. Как всегда широко используется однопараметрическая теория Е. Айфантиса.

В работе А. Ватульян с соавторами [44] приведено решение термоупругой задачи для цилиндра с термозащитным покрытием, отмечается необходимость учета влияния градиентного параметра при оценке прочности покрытия. Аналогичная термоупругая плоская задача рассмотрена также в работе [45].

Развитие вариационного принципа Л. Седова для построения различных диссипативных моделей, позволяющее получить обобщение различных законов теплопроводности, в том числе градиентную модель теплообмена, предлагается в работе [46].

Задачи с поврежденностью, фазовыми превращениями и др. Уравнения неравновесной термодинамики с внутренними параметрами состояния для градиентной теории упругости представлены P. Van в работе [47]. Вариант градиентной теории упругости со скалярным параметром поврежденности развивается в работе [48]. Модель дилатационной теории упругости применительно к чистому изгибу балки, соответствующая частному случаю среды с микроструктурой Миндлина, развивается в работе [49].

Задачи электроупругости в рамках градиентной упругости рассмотрены в работах А. Ватульян с соавторами [50,51]. Оценка напряженно-деформированного состояния, индуцированного фазовым превращением в магнии на основе градиентной теории упругости, проведена в работе [52], где получено аналитическое решение для одноосной деформации тонкого слоя.

Идентификация параметров неклассических теорий упругости. Для практического применения градиентных теорий требуется разработка достоверных методов идентификации дополнительных материальных констант. Идентификация параметров может осуществляться различным образом, в литературе выделяются несколько основных подходов.

Сравнение результатов континуального и дискретно-атомистического моделирования проведено в работе [53]. Использование потенциалов межатомного взаимодействия позволяет определять параметры градиентной теории, приводится пример идентификации для двухфазного композита W-Si [54].

Испытания образцов с различной длиной нанесенных трещин или с различным размером дефектов (метод Васильева–Лурье) предполагает сравнение соответствующих расчетных и экспериментальных данных, в том числе измерение двухмерного или трехмерного поля деформаций вблизи дефектов на поверхности образца [55]. Подобный подход обсуждается в работе [56].

Наиболее распространенным подходом является аналогичный подход, когда оценка параметров для микро- и нано-композиционных структур производится путем измерения поля деформаций (измерение двухмерного или трехмерного поля координат на поверхности образца) изучаемого объекта и сравнения данных с численными (в частном случае, аналитическими) результатами. Такие подходы отражены в различных работах, например [57, 58].

Ниже будет рассмотрена задача деформации тонкого слоя под действием собственного веса для физических уравнений Е. Айфантиса, решение которой в совокупности с инструментальными измерениями позволяет идентифицировать градиентный параметр.

Одноосная деформация тяжелого слоя

Рассмотрим одноосную деформацию тонкого слоя толщиной Z 1 < 1мкм под действием силы тяжести. Такая задача позволяет получить аналитическое решение и может служить основой для оценки градиентного параметра при наличии соответствующего инструментального сопровождения.

Связь между напряжениями и деформациями для максимально простого варианта градиентной теории упругости (Е. Айфантис, [19]) в одномерном варианте (одноосной деформации вдоль оси Z, рис. 1) для декартовой системы координат можно записать как

az = Esz + LE

de_z dz ’

где E – модуль упругости; L – градиентный параметр, имеющий размерность длины; a_z, £_z - компоненты тензора напряжений и деформаций, соответственно.

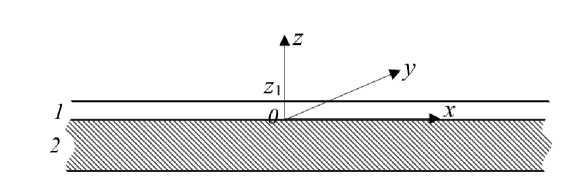
Рис. 1. Одноосная деформация тонкого тяжелого слоя (1), лежащего на абсолютно твердом основании (2)

Рассмотрим тяжелый однородный слой (рис. 1), расположенный в диапазоне

—от < X <  +от; —от <у< +от; 0 < Z < Z 1 ,              (3)

тогда с учетом направления оси z от точки 0 в сторону Z 1

° z = -Y(Z 1 — z) ,                               (4)

где y - удельный вес.

Общее решение уравнения (2) с учетом (4) имеет вид

£_z = Cexp(- ^ )+ ^ (z-Z i -L).                   (5)

Интегрируя (5), получим общее выражение для перемещения:

U z =-CLexp(- ^z )+^(z - z i -L) ² + C i .                 (6)

L/ 2c

Постоянные интегрирования C, C 1 в решении (6) определяются из граничных условий на границах слоя. Классическое граничное условие касается перемещения на границе u_z(z = 0) = 0. Откуда следует, что

C i = CL-^(z i + L) ² .                         (7)

Возникает вопрос о дополнительном граничном условии для определения постоянной C . Казалось естественно предположить, что на свободной границе Z 1 деформация дг₇

£z(z = z1) = 0 , что приводит к условию — (z = z1) = 0 согласно (2), и соответствует отсутствию напряжения на свободной границе az(z = z1) = 0. В этом случае выражение для деформации принимает вид

£ z = ^^L exp( ^z1^^z ) + ^ (z-z i -L).                   (8)

Анализ выражения (8) показывает, что деформация является положительной E_z >  0 , что, конечно, не имеет физического смысла, поскольку слой сжимается под действием силы тяжести.

Следовательно, необходимо задавать деформацию (или ее производную) на границе z = 0, где отсутствуют перемещения. Вариант граничного условия E_z(z = 0) = 0 также приводит к не физическому следствию E_z > 0. Подходящим вариантом является требование ^ (z = 0) = 0 для которого постоянная C = -у. В этом случае деформация и перемещение принимают вид:

Ez^exp^-^+^z-z i -L)              (9)

U z = ^-L- [1-exp(- z )]+- — z⁽z-2z i -2L⁾.              (10)

Полученные выражения (9), (10) можно представить в безразмерном виде:

Е

z

= n^exp (-£) + ^i« -

^ 2

-1);

U z /z i

= ЩП2 {1

- exp ("^)] + ¹ ^ 1 <« - 2^ 2

-2),

где Я 1 = ^, Я₂ = ^, < = ^. Л           Z i        Z 1

Распределение деформации (11) по толщине слоя при п 1 = 0,01 для различных значений параметра п₂ (соответственно, градиентного параметра L) показано на рис. 2.

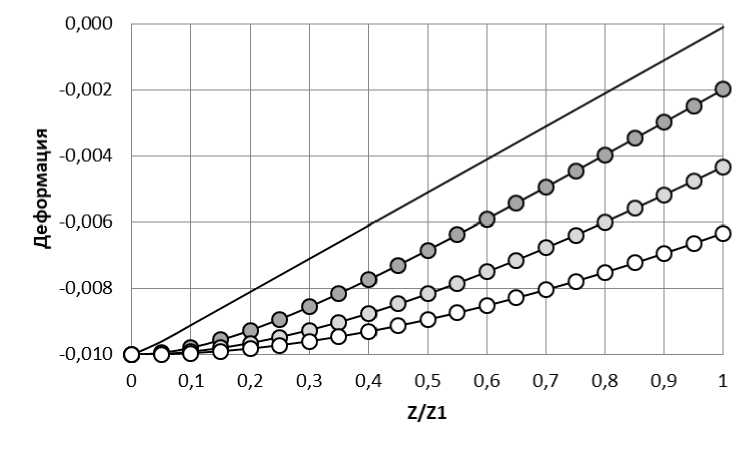
Рис. 2. Распределение деформации по толщине тяжелого слоя: л₂ = 1 - белый круг; 0,5 -светло-серый круг; 0,2 – темно-серый круг; 0,01 – линия без маркера (классическое решение)

Наблюдается сильное отличие классического решения от решений согласно градиентной теории при различных параметрах п₂ (L).

Распределение относительного перемещения (12) по толщине слоя при тех же параметрах показано на рис. 3.

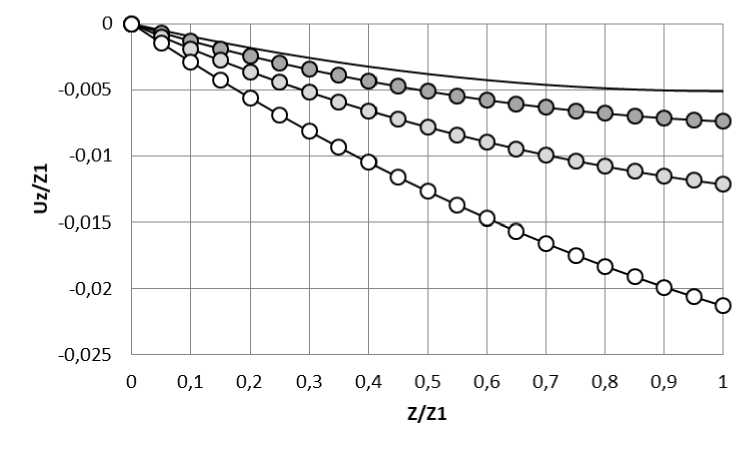
Рис. 3. Распределение относительного перемещения по толщине тяжелого слоя: л₂ = 1 – белый круг; 0,5 – светло-серый круг; 0,2 – темно-серый круг; 0,01 – линия без маркера (классическое решение)

Видно, что на свободной границе тяжелого слоя отличия в перемещениях по градиентной и классической теории могут достигать от 1,5 до 4 раз. Подобные отличия могут быть замерены инструментально с целью определения градиентного параметра L.

Например, для низкомодульного материала (полимер, клей) при толщине слоя Z 1 около 1 мм величина л 1 может достигать 10 -4 . При этом значении л 1 расчеты по представленной модели дают величину максимального перемещения границы слоя u_z (z 1 = 1) = 0,5 мкм для л₂ = 0,01 (классическое решение) и u_z(z 1 = 1) = 2 мкм для л₂ = 1 (градиентная теория).

Пусть тонкий слой низкомодульного материала приклеен к массивной пластине. Пусть толщина низкомодульного слоя в случае, когда массивная пластина находится внизу, равна h 1 . А соответствующая толщина, когда массивная пластина находится вверху, равна h₂ . Тогда

h2-h1 = 2uz(z1 = 1 ).                       (13)

Именно собственный вес слоя определяет разность величин h₂ — h 1 в (13), которая находится в пределах от 1 мкм до 4 мкм, что может быть замерено инструментально. В зависимости от полученного результата (в том числе с помощью графиков рис. 2) можно оценить величину л₂ и градиентный параметр L.

Заключение

Представлен обзор исследований по неклассическим (градиентным) теориям упругости. Рассмотрены вопросы общей теории и различные приложения, в частности, использование упрощенных моделей применительно к микро- и нано-структурным материалам. Отдельное внимание уделено методам идентификации параметров градиентных моделей.

В рамках упрощенной модели Е. Айфантиса поставлена и решена задача одномерной деформации тонкого слоя под действием собственного веса. Предложен способ определения градиентного параметра на основе полученного решения.