Градиентный метод расчета потерь направляющей электродинамической структуры с неидеальными экранирующими поверхностями

Известно, что на характеристики направляющих структур существенное влияние оказывает качество обработки экранирующих поверхностей. При этом по мере повышения частоты требования к качеству обработки этих поверхностей возрастают и становятся соизмеримыми с технологическими возможностями. В связи с этим постоянно растет интерес к изучению влияния шероховатости поверхности на распространение волн в экранированных структурах с учетом конечной проводимости металла [1–3]. Как правило, описание моделей шероховатых поверхностей проводников производят, представляя профили шероховатостей в виде простых геометрических фигур. В некоторых моделях для упрощения анализа эти фигуры располагают периодически. Оценка потерь из-за шероховатостей часто сводится к вычислению поправочных коэффициентов. В данной работе предлагается модификация градиентного метода для определения влияния шероховатости поверхности на затухание волн в экранированных структурах.

• 1.    Существующие модели

• а) Первой широко известной моделью для учета потерь, вызванных шероховатостью поверхности, стала модель Моргана, представляющая собой периодическую структуру типа зуба пилы [4]. Главное предположение в этой модели заключалось в том, что ток течет по краю шероховатой поверхно-

сти, что приводит к увеличению пути, проходимо-

го током, а значит, и к дополнительным потерям мощности. Морган, используя метод конечных разностей при решении задачи для своей струк-

туры, вывел отношение потерь мощности, рассеянной в проводнике с шероховатостью ( а _шер ), к мощности, рассеянной в проводнике с гладкой поверхностью ( а _глад ). Позже Хаммерстад и Джонсон получили эмпирическое выражение, основанное на результатах Моргана, используя только один

параметр неровности – ее среднеквадратичную

высоту ( h _ср) [7]:

^а шер ^а глад

где 5 - толщина скин-слоя. Однако полученное выражение насыщается, когда значение коэффициента K достигает двух. На практике же влияние шероховатости может быть более чем в два раза.

б) Модель полусфер, предложенная Холом, предполагает моделирование шероховатой поверхности проводника в виде полусфер, выступающих из плоскости проводника [5]. Задача рассеяния плоской волны от полусферического выступа

на плоскости решается методом зеркальных отображений. В итоге поправочный коэффициент задается в следующем виде:

K =

Re п

+

+

Ц о ю5

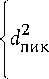
^^^^^^в

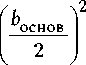
Ц 0 ^ю5 >2

4 ^ пик

поверхности изменяется в обоих горизонтальных направлениях. В этой работе авторы вывели формулу для поправочного коэффициента:

где dпик — расстояние между пиками шероховатостей; b – длина основания неровности, оснон k - волновой вектор; а1 и Р1 - коэффициенты рассеяния первого порядка (они зависят от еще

к = 1 + — 52

^^^^^^в

да да                      / ।;X

- 4f f w ( k x , k y )Re Pi - k² x - k y dk x dk y ,

0 0              v V5

одного геометрического параметра – высоты не- ровности), п =

Ц о

.

\ ^ео ^е '

Таким образом, этот метод основан на трех входных параметрах и требует трех статистических измерений.

• в)    Схожей с вышеописанной моделью является

модель «снежного кома», предложенная Хурэем. Она предполагает моделирование шероховатой поверхности в виде пирамидального набора сферических частиц (снежных комков) на поверхности проводника [6]. Задача рассеяния и поглощения решается аналогично модели полусфер, но для каждой сферы отдельно. Обязательными параметрами являются диаметры сфер и их количество N, приходящееся на площадку. Используя принцип суперпозиции, можно получить результирующие потери в подобной структуре. Поправочный коэффициент шероховатости записывается следующим образом:

к =

N

X4ик +z Reч{(«1 + ei)

_______________ n = 1       ^14K ____________

Ц о ®8 ,2

4 ^d пик

.

Сложность этого метода связана с тем, что основные параметры модели - диаметр сфер внутри пирамидок и их количество на площадке - невозможно наблюдать при измерении.

• г)    Цанг с соавторами осуществил более сложный анализ проблемы шероховатости поверхности [7]. В их работе были проанализированы двумерные случайные шероховатые поверхности на основе метода малых возмущений второго порядка и численного метода моментов. Затем был выполнен расчет коэффициента поглощения мощности для шероховатости поверхности с помощью гауссовой и экспоненциальной корреляционных функций. Расчеты и анализ показали, что коэффициент, описывающий потери, зависит от трех параметров: среднеквадратичной высоты, длины корреляции и корреляционной функции. После этого данный подход был распространен на анализ шероховатости трехмерной поверхности, где высота

где W ( k x , k y ) - функция спектральной плотности мощности.

• д)    Еще в одной работе [8] предлагается подход, основанный на концепции парциальных волн Бриллюэна и позволяющий учесть случайную шероховатость поверхности произвольной формы. В соответствии с ним задача нахождения затухания собственных волн направляющих электродинамических структур с шероховатыми экранирующими поверхностями сводится к достаточно хорошо исследованному случаю структур с идеально гладкими поверхностями. Эквивалентность реальной шероховатой поверхности и гладкой поверхности достигается внесением поправки в удельную проводимость материала последней, обеспечивающей равенство коэффициентов отражения электромагнитной волны от рассматриваемых поверхностей. Средний коэффициент отражения от шероховатой поверхности и коэффициент отражения от гладкой поверхности связаны соотношением

да

г(9) = г(о) J exp(iko2^cos9)to(^)d^, (5) —да где Г (о) - коэффициент отражения от гладкой поверхности; 0 - угол падения волны; ^ - высота шероховатости; м(с) - плотность вероятности.

Тем самым найти затухание волны, вызванное шероховатостью поверхности, можно, внося поправки в удельную проводимость материала экрана.

• е)    В статьях Голда и соавторов описана градиентная модель, которая не предполагает наличия резкой границы между диэлектриком и проводником [9]. Шероховатость моделируется как непрерывный переход проводимости от практически нуля в диэлектрике до объемной проводимости металла. Полагая, что профиль шероховатости для большинства поверхностей имеет нормальное распределение, градиент проводимости выражается, используя один метрологический параметр шероховатости – среднеквадратичную высоту h _ср.

  о ( х ) = п _мет j pDFdu =

  -да

  
  

  ^о мет

  
  

  exp

  
  

  -да

  
  

  ср

  
  

  du .

  
  

  Выражение для скин-эффекта на шероховатой поверхности выводят из уравнений Максвелла для гармонических полей при проводимости, зависящей от местоположения о ( х ). Предполагая проводник немагнитным с поверхностью в плоскости yz , приходят к дифференциальному уравнению только в одном измерении:

  д 2 B y д д B y

  —/ + j ®Ц о о ^B _y - —In ^о— ^_ = 0. (7) д _х ² y д х д х

  В этом выражении третье слагаемое получается из-за проводимости, зависящей от местоположения о ( х ). Без третьего слагаемого о будет просто постоянной величиной и получится уравнение Гельмгольца, описывающее классический скин-эффект на идеально гладких поверхностях.

  
  
  

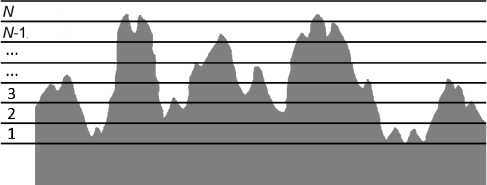
  Рис. 1. Разбиение шероховатой поверхности на слои

  Fig. 1. Splitting a rough surface into layers

  
  

  Исследование отражения электромагнитной волны от рассматриваемой шероховатой поверхности проводится методом ориентированных графов, который позволяет учесть многократные отражения волны от границ каждого слоя. Ориентированный граф рассматриваемой многослойной структуры представлен на рис. 2.

  Элементы матриц, описывающих границы меж-

  
  

  2. Предлагаемая модель

  В данной работе предлагается модификация градиентного метода для определения влияния шероховатости поверхности на затухание волн в экранированных структурах. Любую шероховатую поверхность можно разбить на слои, приняв за начало разбиения линию, проходящую через точку максимальной глубины впадины профиля, и сделав последним слоем разбиения слой, включающий в себя точку максимальной высоты пика профиля (рис. 1). При этом эффективная проводимость каждого получившегося слоя будет находиться в интервале от проводимости металла до проводимости воздуха, изменяясь от перового слоя к N -му. Характер изменения эффективной проводимости от слоя к слою определяется профилем распределения шероховатостей.

  
  

  ду соседними слоями, находятся в соответствии с формулами Френеля:

  _Г _ Z m ( ^ю,^о ) ^- Z m + 1 ( ^ю,^о )

  ¹² Z m ( ^ю, ^о ) ⁺ Z m + 1 ( ^ю,^о ) ’

  
  

  _Г _ Z m + 1 ( ю ^о ) ^- Z m ( ^ю>^о ) ²¹    Z m + 1 ( ^ю, ^о ) ⁺ Z m ( ^ю,^о ) ’

  2 Z ( ю, о )

  у __________ ^m \    / ______

  ¹²    Z m ( ^ю>^о ) ⁺ Z m + 1 ( ^ю>^о ) ’

  ( ю о )

  
  

  ^Т 21

  
  

  Z m ( ^ю>^о ) + Z m ( ^ю-^о )

  
  
  
  

  где m - номер слоя разбиения; Г - коэффициент отражения; Т - коэффициент прохождения.

  После этого можно строить матрицы рассеяния и матрицы прохождения для каждого полученного при разбиении слоя. Важным свойством матриц передачи является то, что матрица каскадного соединения ряда элементов равна произведению матриц передачи этих элементов. Таким образом,

  
  

  Среда 1                Среда 2                   Среда 3                 Среда 4

  АВС

  
  

  ->--Q----

  -1—>--Q------->-

  —о----н

  -^—о------>-

  —о-----1—

  >—о-->

  Ё+

  \

  ^12 /12

  1                   / I 7*21

  e-k2d 'г21 e-k2d

  \

  Тгз /23

  / 7*32

  ^—кз<1 Гз2 ^—^3^

  \

  7’34 | /34

  ё: Г43

  ЁГ

  bl

  |           а2

  ^2           I

  а3

  ^3           I

  «4 Ё;

  Рис. 2. Ориентированный граф модели шероховатой поверхности

  Fig. 2. Oriented graph of a rough surface model

  
  
  

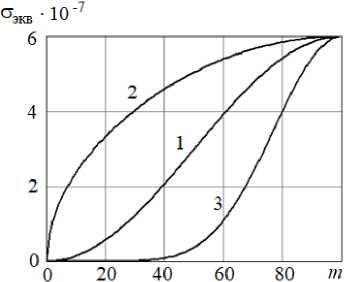
  Рис. 3. Зависимость удельной проводимости от номера слоя

  Fig. 3. Dependence of the conductivity on the layer number

  
  

  о

  JKB

  
  

  4 toS o

  —

  /1 — 4(1 —

  ^ 1,1

  ) 2

  
  

  .

  
  
  
  

  Полученную таким образом эквивалентную проводимость можно либо подставить в известные выражения для вычисления потерь в волноводах, либо использовать при моделировании направляющих структур в САПР. В случае основной волны прямоугольного волновода можно учесть шероховатость экранирующих поверхностей, подставив эквивалентную удельную проводимость в известное выражение для коэффициента затухания:

  
  

результирующая матрица передачи равна произведению матриц передачи отдельных слоев.

Соответствующая ей матрица рассеяния дает коэффициент отражения волны от рассматриваемой структуры, что позволяет найти эквивалентную проводимость рассматриваемой шероховатой поверхности, то есть проводимость идеально гладкой поверхности, имеющей такой же коэффициент отражения, как и шероховатая поверхность. Такое определение эквивалентной проводимости, основанное на концепции парциальных волн Бриллюэна, представляется наиболее адекватным для экранированных направляющих структур.

В случае направляющих электродинамических структур материал экранирующих поверхностей имеет высокую удельную проводимость, что позволяет аппроксимировать зависимость коэффициента отражения от частоты и получить приближенное аналитическое выражение для эквивалентной удельной проводимости:

a =

to ------------

\ ®° экв ^ 0

1 b In c 1+ I

2 a ( a to J cb 1

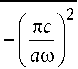
где a и b – поперечные размеры волновода.

На рис. 3 в качестве примера представлен результат расчета профиля эквивалентной удельной проводимости для различных профилей шероховатостей поверхности.

С использованием предложенной методики проведен расчет потерь в прямоугольном волноводе сечением 1,1 × 0,55 мм при шероховатостях экранирующих поверхностей 1 мкм, 0,5 мкм и 0,1 мкм для приведенных профилей шероховатостей. Результаты расчета показаны на рис. 4–6.

Как видно из графиков, погонные потери волновода зависят не только от величины шероховатостей экранирующей поверхности, но и от их профиля.

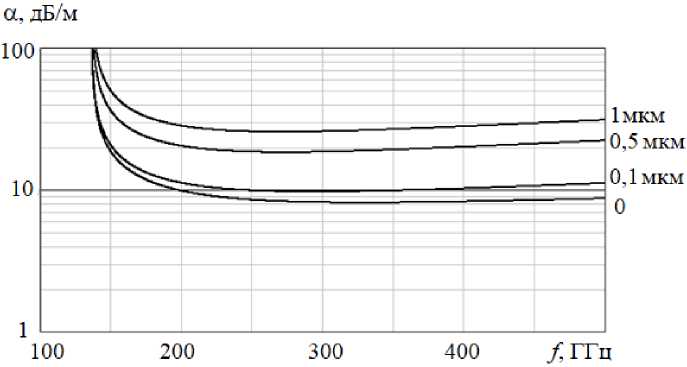
Рис. 4. Зависимость от частоты погонных потерь прямоугольного волновода сечения 1,1 × 0,55 мм с шероховатыми стенками 1-го профиля

Fig. 4. Dependence on the frequency of linear losses of a rectangular waveguide with a cross section of 1,1 × 0,55 mm with rough walls of the 1st profile

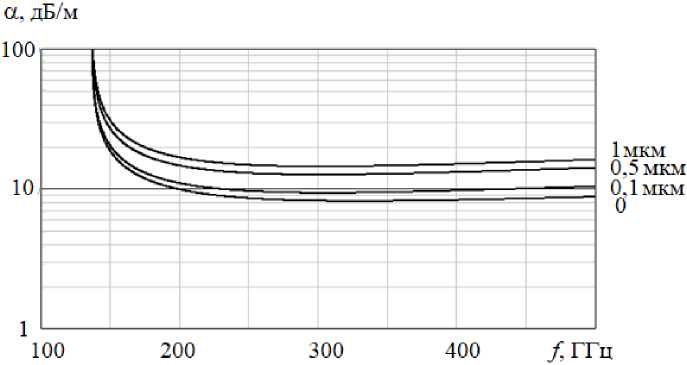
Рис. 5. Зависимость от частоты погонных потерь прямоугольного волновода сечения 1,1 × 0,55 мм с шероховатыми стенками 2-го профиля

Fig. 5. Dependence on the frequency of linear losses of a rectangular waveguide with a cross section of 1,1 × 0,55 mm with rough walls of the 2nd profile

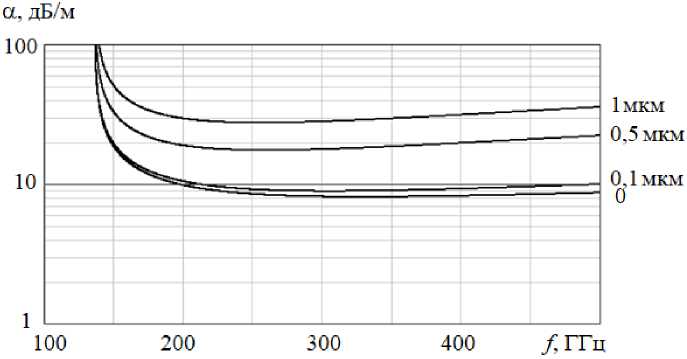
Рис. 6. Зависимость от частоты погонных потерь прямоугольного волновода сечения 1,1 × 0,55 мм с шероховатыми стенками 3-го профиля

Fig. 6. Dependence on the frequency of linear losses of a rectangular waveguide with a cross section of 1,1 × 0,55 mm with rough walls of the 3rd profile

Заключение

В данной работе рассмотрен вопрос оценки потерь в электродинамических направляющих структурах с шероховатыми экранирующими поверхностями. Представлено описание наиболее интересных подходов и предложена новая методика расчета, основанная на концепции парциальных волн Бриллюэна. С помощью разработанной методики получено простое выражение для экви- валентной проводимости шероховатой поверхности, которое может быть использовано в известных выражениях для погонных потерь или при моделировании различных направляющих структур в САПР. Приведены результаты расчетов для прямоугольного волновода с экранирующими поверхностями с шероховатостями различного профиля. Показано, что на величину потерь влияет не только величина неровностей, но и их распределение.