Графический способ определения фактического удельного коэффициента теплоотдачи ограждающих конструкций

Как было определено в статье [1], для повышения точности определения теплозащитных качеств термически неоднородных ограждающих конструкций в натурных условиях наиболее целесообразно определять фактический приведенный коэффициент теплоотдачи внутренней поверхности. При этом инструментально измеряются температура внутреннего воздуха и средневзвешенная температура исследуемой поверхности, например, при помощи тепловизора, а также определяется относительный коэффициент излучения (степень черноты), который для большинства наиболее часто используемых в качестве внутренней отделки строительных материалов известен из справочных материалов. В данном случае исследуются участки ограждающей конструкции с равномерной степенью черноты, т.е. с одинаковой отделкой. Затем, после нахождения коэффициентов теплоотдачи отдельных участков, вычисляется средневзвешенный коэффициент всей исследуемой поверхности в целом.

Таким образом, приведенный коэффициент теплоотдачи внутренней поверхности термически неоднородной конструкции с одинаковой степенью черноты а , определяется по формуле

< = 1,66 ■ V t в - т С + С о ■ с , [ 0,81 + 0,005 ( t , + т с ) ] ,                   (1)

где t _в – температура внутреннего воздуха, °С;

т,^р - средняя температура внутренней поверхности исследуемого участка, °С;

С _о – коэффициент излучения абсолютно черного тела, равный 5,77 Вт/м²°К4;

£ _в - степень черноты исследуемого участка, б/р.

Расчетная формула (1) довольно громоздкая, имеет сложное математическое выражение, так как содержит множитель в виде кубичного корня, и трудоемка для простых арифметических расчетов. Поэтому для упрощения расчетов можно воспользоваться графическим методом определения а ”^Р . в

Из формулы (1) видно, что теплообмен внутренней поверхности стены с окружающей средой, т.е. с внутренним воздухом, происходит двумя способами: конвективной и лучистой теплопередачей. При этом каждую составляющую рассмотрим в отдельности.

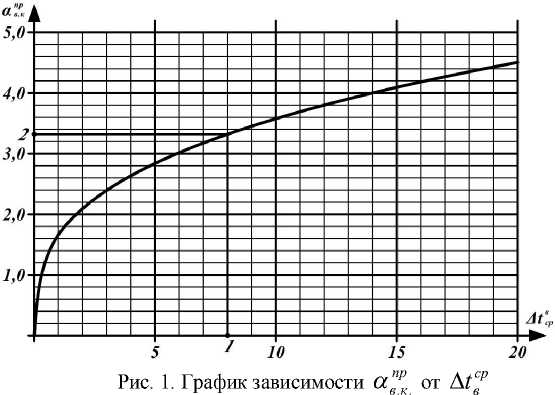
Как известно из теории строительной теплофизики, среднее значение (приведенное) коэффициента теплоотдачи свободного конвективного теплообмена без особой погрешности определяется по формуле турбулентного режима теплопередачи [2]

ар = 1,66 • V te - тс, в. к. в в и он зависит только от перепада температур между температурой внутреннего воздуха и средневзвешенной температурой внутренней поверхности Atcgp = tв - ТР . График зависимости а™. от

A t Bp имеет вид параболы (рис.1).

Приведенный коэффициент лучистой теплоотдачи определяется по формуле

«7,= C o • 8 в [0,81 + 0,005( t₆ + Т с )] (2) и, как видно, зависит от трех параметров - t в ,т^{с р} и в в .

На практике значения этих параметров находятся в некоторых интервалах, которые определяются исходя из комфортности условий нахождения людей в помещении. Так, температуру внутреннего воздуха в зависимости от назначения зданий и сооружений можно рассматривать в пределах 1 _в =15-25°С. Средневзвешенная температура внутренней поверхности наружных стен зависит от конструктивного решения ограждающей конструкции, т.е. наличия в ней теплопроводных включений, и колеблется в больших пределах, разница между ними может достигать довольно больших значений. Исходя из наиболее вероятных средневзвешенных температур внутренней поверхности ограждений, диапазон перепадов температур A t ^cc^p = t в - т^{с р} выбираем в интервале от 0 до 20°С.

Степень черноты наиболее распространенных отделочных материалов, применяемых для отделки стен, находится в пределах 0,85-0,98 [2, 3].

Подставив реальные значения t в , т^{с р} и в в в уравнение (2), можно рассчитать приведенный коэффициент лучистой теплоотдачи ограждающей конструкции для определенных условий эксплуатации здания.

Для удобства анализа зависимости приведенного коэффициента теплоотдачи от различных факторов рассмотрим ее в зависимости от перепада температур Atcp = tв - тср . Кроме того, в такой же зависимости рассматривается приведенный коэффициент конвективной теплоотдачи annpK . Поэтому появляется возможность наглядно показать зависимость коэффициентов конвективной и лучистой теплоотдачи панели на одном графике. В связи с этим расчетную формулу для определения приведенного коэффициента лучистой теплоотдачи внутренней поверхности (2) преобразуем к виду aвn.pл.=5,77εв[0,81+0,005(2tв - Δtвcp)].                                   (3)

Тогда уравнение (1) для определения общего приведенного коэффициента теплоотдачи внутренней поверхности будет иметь вид aвnp =1,663 Δtвcp +5,77εв[0,81+0,005(2tв-Δtвcp)].                               (4)

По формуле (3) вычислены все значения a _в ⁿ _. ^p _{л .} для всех наиболее часто встречающихся параметров t _в , Δ t _в ^cp , ε _в . Расчеты произведены при температуре внутреннего воздуха от 15 до 25°С, ε _в от 0,86 до 1,0 и Δ t _в ^cp от 0 до 20°С. Результаты расчетов a _в ⁿ _. ^p _{л .} t _в = 18°С приведены в таблице 1. Здесь для сравнения даны результаты расчетов при ε _в = 1, т.е. абсолютно черного тела, которого в природе не существует.

Кроме того, проведены расчеты a _в ⁿ _. ^p _{л .} при Δ t _в ^cp , равном 0 и 20°С, и температурах t _в от 15 до 25°С, ε _в от 1,0 до 0,86 (табл. 2).

Следует заметить, что значение Δ t _в ^cp =0°С встречается при исключительных случаях, например при отсутствии теплового потока или перепада температур на противоположных сторонах ограждения, т.е. при τ _в ^cp = τ _н ^cp , или при очень большом сопротивлении теплопередаче, т.е. R o^np =∞ .

Таблица 1

Приведенные коэффициенты лучистой теплоотдачи при tв = 18°С, Δtвcp= 0-20°С, εв= 0,86-1,0

Δ tbcp , °С	τ в °С	a в n . p л . , Вт/м2°С при ε в
		0,86	0,88	0,9	0,92	0,94	0,96	0,98	1,0
0	18	4,912	5,027	5,141	5,255	5,37	5,484	5,598	5,712
2	16	4,862	4,976	5,089	5,202	5,316	5,429	5,541	5,655
4	14	4,813	4,925	5,037	5,149	5,261	5,373	5,485	5,597
6	12	4,763	4,875	4,985	5,096	5,207	5,318	5,428	5,539
8	10	4,714	4,824	4,933	5,043	5,153	5,262	5,372	5,481
10	8	4,664	4,773	4,881	4,99	5,099	5,207	5,305	5,424
12	6	4,614	4,722	4,829	4,937	5,044	5,152	5,259	5,366
14	4	4,565	4,671	4,777	4,884	4,99	5,096	5,202	5,308
16	2	4,515	4,621	4,725	4,831	4,936	5,041	5,146	5,25
18	0	4,466	4,57	4,674	4,778	4,881	4,985	5,089	5,193
20	-2	4,416	4,519	4,622	4,724	4,827	4,93	5,037	5,135

Таблица 2

Приведенные коэффициенты лучистой теплоотдачи при Δ t _в ^cp = 0 и 20°С, t _в = 15-25°С, ε _в = 0,86-1,0

t в , °С	Δ t вcp , °С	a в n . p л . , при ε в
		0,86	0,88	0,9	0,92	0,94	0,96	0,98	1,0
15	0	4,764	4,874	4,985	5,096	5,207	5,318	5,428	5,539
	20	4,267	4,367	4,466	4,565	4,664	4,764	4,863	4,962
16	0	4,813	4,925	5,037	5,149	5,261	5,317	5,485	5,597
	20	4,317	4,418	4,518	4,618	4,719	4,819	4,92	5,02
18	0	4,912	5,027	5,141	5,255	5,37	5,484	5,598	5,712
	20	4,416	4,519	4,622	4,724	4,827	4,93	5,033	5,135
20	0	5,012	5,128	5,245	5,361	5,478	5,594	5,711	5,828
	20	4,516	4,621	4,726	4,831	4,936	5,04	5,146	5,251
22	0	5,111	5,23	5,348	5,468	5,586	5,705	5,824	5,943
	20	4,615	4,722	4,829	4,937	5,044	5,151	5,259	5,366
24	0	5,21	5,331	5,453	5,574	5,695	5,816	5,937	6,058
	20	4,714	4,824	4,933	5,043	5,153	5,262	5,372	5,281
25	0	5,26	5,382	5,505	5,627	5,749	5,871	5,994	6,116
	20	4,764	4,874	4,985	5,096	5,207	5,318	5,428	5,539

Результаты расчетов a _в ⁿ _. ^p _{л .} можно представить в виде графиков в зависимости от различных параметров, которые будут представлять собой семейство разнонаправленных прямых.

На рисунке 2 представлена номограмма, где по оси ординат отложен приведенный коэффициент лучистой теплоотдачи a ^np , вправо по оси абсцисс отложен перепад температуры на внут- в . л .

ренней поверхности ограждающей конструкции Δtвcp от 0 до 20°С. На этой системе координат приведены графики зависимости aвn.pл. от Δtвcp при tв = 15оС и в диапазоне степени черноты от 0,86 до 1,0. Таким образом, график зависимости anp от Δtcp имеет наклон вниз, что показано на в .л              в рисунке 2. Графики при меньших значениях εв расположены ниже.

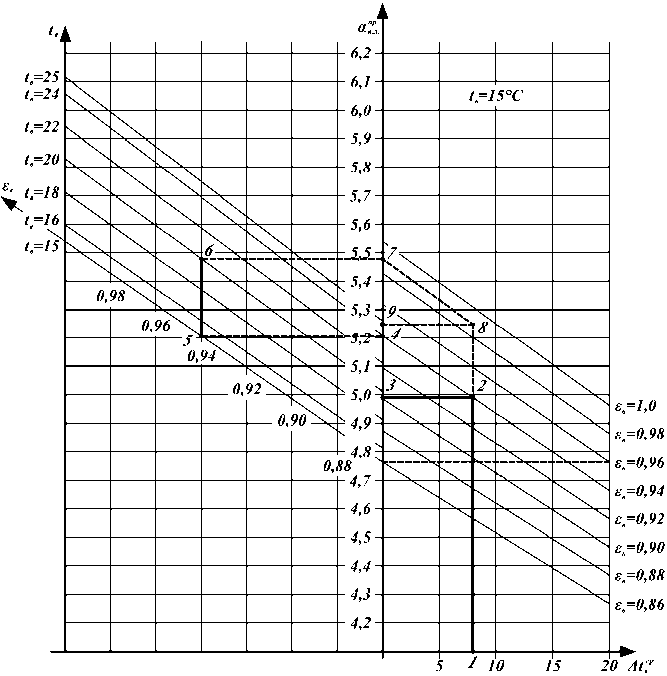
Рис. 2. График зависимости a ^np от Δ t ^cp при t =15°С в . к            в             в

С левой стороны от оси ординат расположена вспомогательная ось, где отложена температура внутреннего воздуха t _в , причем таким образом, что уровни при t _в = 15 и 25 °С для ε _в =0,86 совпадают с нижней линией графиков правой части номограммы (см. табл.2). Для каждой температуры внутреннего воздуха проведены соответствующие линии. Начало этого вспомогательного графика совпадает с графиком зависимости a _в ⁿ _. ^p _{л .} от Δ t _в ^cp при наименьших ε _в = 0,86 и t _в = 15°С и Δ t _в ^cp =0°С. На этой прямой, направленной наклоном вверх, условно принятой за вспомогательную ось абсцисс, отложены значения ε _в в левую сторону, причем уровень каждого значения ε _в соответствует значению a _в ⁿ _. ^p _{л .} при Δ t _в ^cp = 0°С, соответствующему ε о основного графика. Выше вспомогательной оси абсцисс расположены графики зависимости a _в ⁿ _. ^p _{л .} от ε _в при более высоких t _в . Таким образом, если основной график позволяет определить a _в ⁿ _. ^p _{л .} от Δ t _в ^cp при t _в =15°С и разных ε _в , то вспомогательный график – сделать поправку a _в ⁿ _. ^p _{л .} при соответствующем t _в . То есть к значению a _в ⁿ _. ^p _{л .} , определенному по основному графику, должна быть прибавлена температурная поправка, определенная по вспомогательному графику.

Для того чтобы показать, каким образом пользоваться предложенной номограммой, в качестве примера определим приведенный коэффициент лучистой теплоотдачи при t _в =18°С, 8 в = 0,94 и A t ^ = 8°С. в

Из точки 1 на оси абсцисс основанного графика (см. рис. 2), соответствующей A t в = 8°С, восстановим перпендикуляр до пересечения с прямой зависимости а вр при заданной 8 в = 0,94. Эта точка пересечения позволяет определить а" в^р _л при t _e = 15°С (т.3). Для определения температурной поправки обратимся к вспомогательному графику. Из точки 5, которая соответствует а в^р_л при 8 в = 0,94, t _в = 15^оС (т. 4), восстановим перпендикуляр до пересечения его со вспомогательной прямой зависимости при заданной температуре t _в = 18°С (т. 6). Отрезок прямой 5-6 является температурной поправкой, на которую должно быть увеличено значение а"^рл , определенное по основному графику (т. 3). Отложив отрезок 5-6 от точки 3 выше, получим истинное значение коэффициента лучистой теплоотдачи (т. 9) при заданных параметрах. Точка 9 может быть найдена графически путем построения точек 7, 8, 9. При этом отрезок прямой 7-8 параллелен отрезку прямой 2-4 , а отрезки 5-6, 4-7 и 2-8 и 3-9 равны между собой.

Коэффициент лучистой теплоотдачи, найденный графическим способом, равный 5,25 Вт/м²°С, хорошо согласуется со значением а"^рл , определенным по формуле (1), который равен 5,261 Вт/м²°С.

Аналогичные номограммы могут быть построены относительно базовых графиков зависимости а^пр_л от A tр , например при t_e = 25°С, т.е. при наибольшей (условно принятой) температуре внутреннего воздуха (рис. 3). В этом случае вспомогательные графики будут направлены вниз, а любое значение a" ⁿ„ при t < 25°С меньше а ”^р при t =25°С и 8 =1,0, т.е. от значения а ”^р , в . л.                 в                                                в . л.                 в                             в                                                             в . л.

найденного по основному графику, должна быть отнята поправочная величина, определенная по вспомогательному графику. Схема определения точки 9 на рисунке 3 аналогична предыдущей схеме при t _в =15°С.

Фактический удельный коэффициент теплоотдачи ограждающих конструкций может быть определен путем сложения а в^рк и а вр , найденными графическими способами по рисункам 1, 2 или 3.

На рассмотренной номограмме, например на рисунке 3, может быть построен график зависимости коэффициента конвективной теплоотдачи а вр от A t р . При этом ось абсцисс будет общей, а ось ординат, на которой отложены в любой пропорции значения а ”Р , направлена вниз. На ..

рисунке 3 график зависимости ав^рк от A t р показан пунктирной линией.

На номограмме, представленной на рисунке 3, в качестве примера приведен способ определения приведенного коэффициента теплоотдачи при заданных параметрах, например A t С = 6°С, t _в = 18°С и 8 в = 0,9. Удельный коэффициент теплопередаче а в^р определяется путем сложения а ^Р и а в ^ , определенных по номограмме ( а в^р = 4,98+ 3,0 =7,98 Вт/м²°С). Полученные данные хорошо согласуются с расчетными ( а_в” ^р = 8,0 Вт/м2°С, погрешность 0,25%) и могут быть приняты для инженерных исследований строительных ограждающих конструкций.

Преимуществом графического способа определения приведенного коэффициента теплоотдачи является то, что исключаются трудоемкие расчеты, это позволяет наглядно представить всю зависимость ав^р от всех трех параметров. Кроме того, на одной номограмме помещается вся информация зависимости а в^р от t_в , 8 в и A tр , что практически невозможно представить в виде таблиц. При этом можно определить ав^р во всем диапазоне рассматриваемых параметров непрерывно, а не дискретно, как это делается по таблицам.

При построении номограмм использованы наиболее широко распространенные значения трех основных параметров – t _в , ε _в и Δ t _в ^cp . В случае если какой-либо из этих параметров не входит в рассматриваемый диапазон, в каждом конкретном случае приведенный коэффициент теплоотдачи определяется расчетным способом по формуле (1) или по специальной номограмме, построенной для заданных параметров.

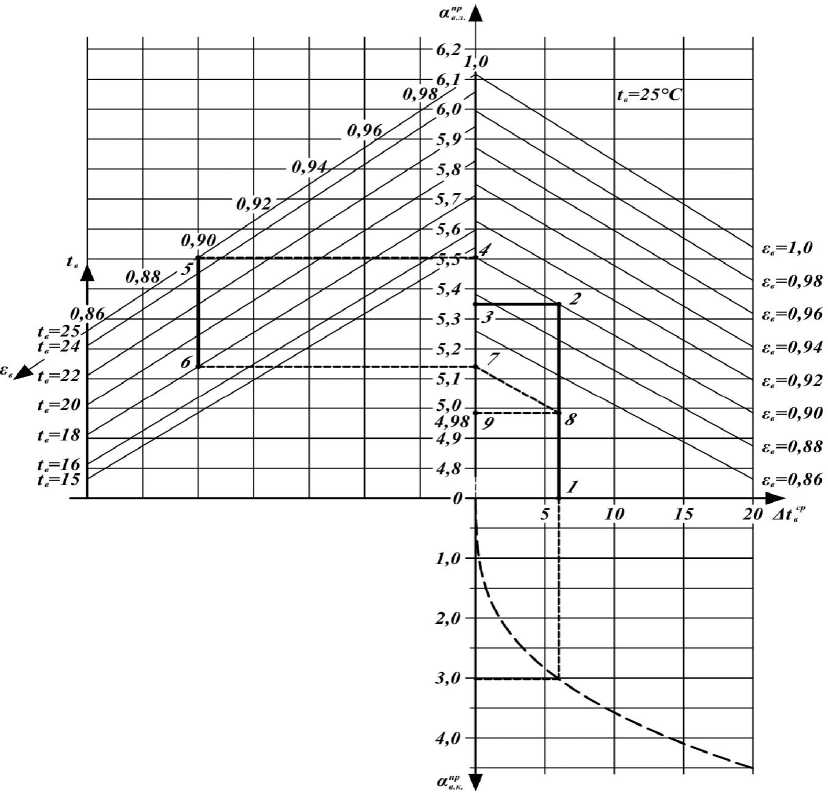
Рис. 3. График зависимости a ^np и a ^np от Δ t ^cp при t =25°С в . л .           в . к .               в                 в