Grand Morrey type spaces
Автор: Samko Stefan G., Umarkhadzhiev Salaudin M.
Журнал: Владикавказский математический журнал @vmj-ru
Статья в выпуске: 4 т.22, 2020 года.
Бесплатный доступ
The so called grand spaces nowadays are one of the main objects in the theory of function spaces. Grand Lebesgue spaces were introduced by T. Iwaniec and C. Sbordone in the case of sets Ω with finite measure |Ω|
Morrey type space, grand space, grand morrey type space, grandizer, partial grandization, mixed grandization, homogeneous kernel, hardy type operator, hilbert operator
Короткий адрес: https://sciup.org/143172460
IDR: 143172460 | УДК: 517.968 | DOI: 10.46698/c3825-5071-7579-i
Текст научной статьи Grand Morrey type spaces
Last decades there were widely investigated the so called grand Lebesgue spaces, introduced in [1]; see for instance, [2–5] and references therein, where such spaces and operators on them were studied in the case of finite measure underlying set. An approach to grand Lebesgue spaces on sets of infinite measure was suggested and developed in [6–10].
-
# The research of S. Samko was supported by Russian Foundation for Basic Research under the grant 19-01-00223 and TUBITAK and Russian Foundation for Basic research under the grant20-51-46003. The research of S. Umarkhadzhiev was supported by TUBITAK and Russian Foundation for Basic Research under the grant 20-51-46003.
-
© 2020 Samko, S. G. and Umarkhadzhiev, S. M.
That idea of “grandization” was also applied in the context of Morrey spaces defined by the norm llf IIlp.^(Q) SUP
(/ f(y) | p dy)
X B( x,r ) '
L ” (0 , diam Q)
we refer for instance to [11–14], see also references therein.
Our goal is to extend the notion of grandization to the spaces L p,q,w (R n ) , with the norm of the type (1), where L ^ -norm is replaced by L q -norm, 1 ^ q < to , see precise definitions in Section 2. Such spaces are usually referred to as Morrey type spaces. These spaces were introduced and studied in [15] and [16]. In the case w(r) = r -A , A > 0 , these space first appeared, though as an episode, in [17, p. 44]. For further studies of operators on L p,q,w (R n ) -spaces we refer, for instance, to [18, 19] and references therein, see also the surveying papers [20, 21] and [22].
We study various approaches to the grandization of Morrey type spaces, with respect to the exponents p and q . This includes partial grandization and mixed grandization. To this end, we deal with “grandizers” a(y) and b(r) in the corresponding variables, see Definitions 3.1, 3.2, 3.3.
We find conditions on the grandizers a and b , which ensure embedding of Morrey type spaces into the introduced grand Morrey type spaces.
In the case of partial grandization with respect the exponent q , we study, in grand Morrey type spaces, the boundedness of a certain class of integral operators K with a kernel homogeneous of degree — n . This class includes, in particular, multidimensional versions of Hardy type and Hilbert operators. Within the frameworks of generalized Morrey spaces, corresponding to the case q = to , a more general class of operators with homogeneous kernel was studied in [23].
We first study such operators in Morrey type spaces (not grand ones) and obtain sufficient conditions and also some necessary conditions for their boundedness. In fact, we obtain a result stronger than just boundedness: we estimate the norms \\ Kf ||L P,q,w ( R n ) via similar one-dimensional norms of spherical means of f . Then we apply the obtained results on the boundedness to grand Morrey type spaces.
In application to the Hardy operators with power weights, the obtained conditions have a form of criterion when w(r) = r -\ A > 0 .
The paper is organized as follows. Section 2 contains necessary definitions. In Section 3.1 we discuss varions ways of grandization of Morrey type spaces L p,q,w (R n ) . In Section 3.2 we provide conditions on grandizers ensuring embedding of Morrey type spaces into grand Morrey type spaces. In Section 4.1 we study the operators K in the Morrey type spaces L p,q,w (R n ) , and in Section 4.2 in grand Morrey type spaces L p,q ) ,w (R n ) , both with application to the Hardy and Hilbert type operators.
2. Preliminaries
Following the known definitions, we introduce the spaces Lp,q,w (Rn), defined by the norm
Lрд-™№Л" sup
x∈E
j w(r)q I j |f (y)|p dy
|x-y| Qq (R+):= ^ w : w is a weight and ∞ / t w(r)q r dr < to for some t > 0 In the cases E = {0} and E = Rn we have the local and global Morrey type spaces, respectively. We do not indicate dependence of the space on the choice of the set E , since it is unessential for our consideration. Only in Section 4 we choose E = {0}. In the special case w(r) = r-A, A > 0, we also use the notation Lp,q,λ (Rn) := Lp,q,w(Rn) w=rл without danger of confusion of notation. For a function w(r) defined on R+, we will use the notation w*(t) := sup wtr>and w.(t) := inf wtr>, t> 0. reR+w(r) xeR+ w(r) Observe that w. Q) = w,^). Obviously w*(r) = w.(r) = w(r), when w(r) = r A, A E R. However, in the case of piece-wise power function wAy(r) = r A(1 + r)A Y ~ I r-γ r < 1, r > 1, where λ, γ ∈ R, we have a gap between w∗and w∗: w.,Y(r) = {r— max{A,7} r—min{A,7}_ r < 1, r > 1, {r-min{A,Y} r < 1 r-max{A,Y}’ r> 1 see e. g. [24, p. 715 ]. 3. Grand Morrey Type Spaces 3.1. Grandization of Morrey type spaces. Everywhere in the sequel, a = a(y) and b = b(r) are weights on Rn and R+, respectively. Definition 3.1. Let 1 < p < to, 1 < q < to, w E Qq (R+) (4) and ^ E L^(Rpq), ^(e,5) > 0 for (e, 5) E Rpq and lim y(e, 5) = 0, (e,5H0,0) where Rp,q := {(e, 5) E R+ : 0 < e < p — 1, 0 < 5 < q — 1}. We define the mixed grand Morrey type space Lp^bq),w(Rn) as the space of functions with the finite norm i Ц/ || ,p),q),wmn. := SuP ^(e,5)SUP La,b (R) (e,S)ERp_q XEE ∞ p ' — , ε q ' — I δ Уw(r)q 5b(r) q j \f(y)|p £a(y)pdy |x-y| dr r . We also say that Lp^bq),w(Rn) is the mixed gandization of the space Lp,q’w(Rn). Note that mixed coordinate-wise grandization of mixed Lebesgue spaces was studied in [25]. Definition 3.2. We define partial grandizations La),q,w(Rn), 1 < p < to, 1 < q < to, and Lp,q),w(Rn), 1 < p < to, 1 < q < to, of the space Lp,q’w(Rn) as the spaces of functions with the finite norm IlfLp^q-w(Rn) :=n/sup, a ' ' 0 ∞ ^(e) sup / w(r)' x∈E \0 p j |f (y)|p-ea(y)F dy I |x-y| q -ε dr r / 1 q , where ^ G L“(0,p — 1), ^(e) > 0 and limE,0^(e) = 0, and |fOl,^(Rn): 0<™p-i ∞ ^(5) sup [ w(r)q-Sb(r)q x∈E q-δ p j |f(y)|pdy |x-y| \ q-S dr r , where ^ G U”(0, q — 1), ^(5) > 0 and lim° ,o ^(5) = 0, respectively. Definitions 3.1 and 3.2 may be generalized in the following direction. Let U C Rp,q be an arbitrary measurable set of points in Rp,q, such that (0, 0) is a limiting point for U. Definition 3.3. Let 1 < p < to, 1 < q < to, ^ G U”(U), ^(e,5) > 0 for (e,5) G U and limuэ(£,°)^(о,о) ^(e,5) = 0. We define the U-grandization ULp^^’w(Rn) of the Morrey type space as the space of functions with finite norm ∞ q-δ I|flluLp),q),w(Rn) := sup a-b v' (e,8)eu δ ^(e,5)sup w(r)q °b(r) ч x∈E ∈E p -ε dr r i \ q-S . / Under the choice U = Rp,q we have the mixed grand Morrey type space introduced in Definition 3.1. Partial grandization from Definition 3.2 formally correspond to the case where U = {(e, 5) : 0 < e < p — 1,5 = 0} and U = {(e, 5) : e = 0, 0 < 5 < q — 1}. In the sequel we use the notation N(f; e,5y.= sup x∈E ∞ j w(r)q-°b(r)q q-δ p -ε \ q-S dr r / for brevity, assuming that p, q, w, a and b are fixed. In case of partial grandization we have N(f; e, 0) and N(f; 0, 5) for b = 1 and a = 1, respectively. Lemma 3.1. I. Let (eo, 5o) G UE0°0 := {(e, 5) G U : 0 < e < eo, 0 < 5 < 5o}, a G L1(Rn) and b G L1(R+, dr), then sup y(e,5) N(f; e,5) < C sup y(e,5) N(f; e,5), (e,5)GU (e,5)GUE0-s0 where C = C(e0,50, 1Ы^1(Rn), ||b|L1(R+, dr)) • II. In the case of partial grandization with respect to the variable r, similarly sup ^(5) N(f ;0,5) < C sup ^(5) N(f ;0,5), 0<° 0<°<°0 where C = C(5o, |b|Li(R+,dr)). <1 We have to estimate sup ^(e,6) N(f; e, 5) — max {Si, S12,S2}, (UW\Ueq,5q where S1 :— sup ^(e,S) N(f; e,6), (e^GUi S12 :— sup ^(e, 5) N(f; e,6), (e,8)EU12 U2 :— {(e,6) € U : e > Eq, 5 < 6q}, S2 :— sup ^(e,S) N(f; e,5), (e,8)EU2 U1 :— {(e,5) € U : e< Eq, 6 > 5q}, U12 : —{(e,5) € U :E > Eq, d > 5q}. For S12, we apply the Holder inequalities in the variables y and r with the expends pp—0 and qq--δδ0, respectively and obtain 1- 1 1- 1 S12 5 sup P(E,j)^a<p--,;,p--0||b|| 1422 (e,5)GU12 () L + r ) X q ∞p ^wM9-80b(r)^0 1 j f(y)|p-eoa(y)0 dy I у Q \Jx—y| - ε0 \ q-5a dr r / 1- 1 sup ^(E,5)|a|L-(ERnp-Eo ||b|| (e,8)EUi2 V 7 1 q-δ 1 q-δ0 L1(R+, dr) sup ^(e, 5) U8)eUe0 ,5° sup ^(e,5) N(e,5). (e, 8)eUe° ,s0 Estimation of S1 and S2 is easier via similar use of the Holder inequality in one variable only. We omit details. >
3.2. Embedding of Morrey type spaces into grand Morrey type spaces.Lemma 3.2. If
Cq :—
∞q
q pδ -1
sup ^(E,5)sup b(r)A(x,r)p ■ 1
(e,8)EU xEE q
dr
-- < TO, r
where A(x,r) :— J|x-y| L'"»1) ^ ULp^-w(Rn) and Bf«uLa>b,,..(,„)< CoBf »LP.q.w(I-). (6) < It suffices to apply the Holder inequalities with the exponents p—^ and q—8 in the inner and outer integrals in the definition of the norm in Definition 3.3. > Theorem 3.1. The conditions a € L1(Rn) and b € L1(R+, dr) are sufficient for the embedding (6) for any choice of the set U. The condition b € L1(R+, dr) is sufficient for embedding of Up’q’w(Rn) into the partial grand space Lp’q)’w(Rn). < It is easy to see that the change of a(y) by Aa(y), A — const > 0, keeps the grand space (up to equivalents of norms). Consequently, we may assume that Ba^Li(Rn) — 1. Then A(r) 2 1 and the statement follows from (5). The embedding into the partial grand space follows from Lemma 3.1. > Remark 3.1. Note that the condition (5) does not assume that a E L1(Rn), bE L1 (R+, dr). In particular, in the case of “partial” grandization in the direction 5 = pe, the embedding (6) holds, if b(r)A(r)q/pE L1(R+, dr). By ACioc(R+) we denote the class of functions ф : R+ ^ R, absolutely continuous on every interval [0, N], N > 0. In Theorem 3.2 we impose the condition sup 0<5 ∞ I δ b^q. dt t 1 q-δ <∞ on the grandizer b. Lemma 3.3. Let ^(5) ^ cS1/4. Grandizer b of the form rµ b(r) = (T+rp r where lr,a (r) = < lnT e, r ln" r, r < 1, r ^ 1, satisfies the condition (7) if 0 < ц < v < to and т,а E R. <1 Let first т = a = 0. We have rδ / b dr r ∞ / Mi-1 rq νδ (1 + r) q dr । ■ । ■. г( "E) c ∼ δ, so that (7) is satisfied. In the case of the presence of the logarithmic factor lT,T (r), it suffices to observe that lT,CT(r) is dominated by (1+142 with arbitrarily small exponents ni > П2 > 0 and the estimate by ^ in (8) does not depend on ц and v, provided 0 < ц < v. > Theorem 3.2. Let 1 ^ p < to and 1 < q < to. Let the grandizer b satisfy the condition (7). The embedding Lp,4,w(Rn) C Lp,4),W(Rn) is strict if w(r) satisfies one of the following assumptions: i) w is decreasing, limr^o w(r) = to and W E ACioc(R+); ii) there exist numbers V1 and V2, 0 < V2 < V1 ^ to, such that w(r)rv1 is almost increasing and w(r)rv2 is almost decreasing. The corresponding counterexample is f (x) = fo(|x|), where /„(,) = A- V 5- [ -2-1^p f0( ) V dr^w(r)pJy for the case i ) and 1 fo(r) = r^ in the case ii ). <1 The case i). For f = fo(|x|) we have [ |fo(|y|)|pdy = c[^\ dp, C = |S n-1|. J J dp |_w(p) |y| By the absolute continuity of w1p we obtain that Therefore, C1p w(r) N(f ;0,5) = C p b(r) q 1 q-δ from which it follows that f G Lp,q),w(Rn), but f / Lp,q,w(Rn). The case ii). In this case we have Л f dy=CJA |y| From the assumptions in ii ) it is easy to obtain that C1 < [ dp< C2 w(r)p J pw(p~)P w(r)p' From the equivalence (9) we obtain that N(f ;0,5) - b(r) q 1 q-δ which completes the proof. >
4. Operators with Homogenous Kernel In this section we choose E = {0} in the definition of the space Lp,q,w(Rn). We consider integral operators Kf(x) = У K (lxl>|y|)f(y) dy, Rn where the kernel is homogeneous of degree -n, i. e. K(t|x|,t|y|)= t nK(|x|, |y|). 4.1. Operator K in Morrey type spaces. In the sequel we use the notation ntf (x) := f(tx), x G Rn, t > 0. It is not hard to check that If -(r) = r w. (?) n tp w Ilf||LP-q-w(Rn) C ||ntf||LP-q-w(Rn) C — 1 • (i) n tp Ilf ||LP,q,w(Rn). л, then w*(t) = —.(t) = t x and ||nt||Lp-q-w(Rn) = tx n/p. In the theorem below we also use the notation ∞ к*(п):= |Sn-11 У sn 1|K(1,s)|w. ^-^ ds 0 and ∞ K.(n):= |Sn- 1| У sn-1|K(1,s)| w. (S^ ds, 0 where |Sn-1| should be replaced by 1 in the one-dimensional case of R+. The following one-dimensional theorem is an immediate consequence of (10). Theorem 4.1. Let 1 C p < то, 1 C q < то and w G ^q(R+). The condition к^(1) < то is sufficient for the boundedness of the operator ∞ Kf (x) = У K(x, y)f (У) dy, x G R+, 0 where K(tx,ty) = t 1K(x,y), t > 0, in the space Lp,q,w(R+) and lKf ||LP-q-w(R+) C ^Wllf^Lp-q-w(R+)- <1 We have ∞ Kf (x) = У K(1,V)f (xy) dy. Then by the Minkowsky inequality we obtain ∞ llKf llLP-q-w(R+) c У K(1>y)|ny f llLP-q-w(R+) dy, 0 whence (11) follows by (10). > For the multi-dimensional case, in the next theorem we provide a statement stronger than just the boundedness in the space Lp,q,w(Rn). More precisely, we estimate the norm ||Kf ||LP,q,w(Rn) via one-dimensional norms of spherical means of f. Theorem 4.2. Let 1 C p < то, 1 C q < то and — G Q9(R+). If /(n) < то, n ^ 1, then q ∞ r pq . ,,1 Г qn(rAq If .. . i I lKf lLP-q-w(Rn) C |Sn-1| P K*(n)\J -Grb I у tn-1|Ф(t)|p dtl dr I , where w) = ISL, / f(ta) da- Sn-1 <1 Note that Kf is a radial function for any f. It is easily seen that for any radial function g(x) = G(|x|) one has Hg^Lp-q-w (Rn) = |Sn 11p ||GP^LP,q,w (R+), (13) where Gp(p) = p(n 1)/pG(p). Furthermore, passing to polar coordinates we have ∞ Kf (x) = |Sn-1| У n— 1 t~‘rK(|x|,t)Фp(t) dt, where n—1 tp фp(t) = |Sn-1| у f(ta) da-Sn—1 Then by (13) we have HKf ||Lp-q-w(Rn) = |Sn11p ||K1Фp|Lp,q,w (R+) where ∞ К1Фр(р) = j 0 K1(p,t)фp(t) dt, n—1 n—1 K1(p, t) = p pt p K(p,t) The kernel K1(p, t) is homogeneous of degree —1, i. e. K1(sp, st) = s1K1(p, t), s > 0. Therefore, we can apply Theorem 4.1 and obtain (12) after easy calculation. > Remark 4.1. The estimate (12) is stronger than the boundedness in Lp,q,w(Rn). Indeed, q ∞ r pq j и in-1^(t)|P <4 dr I <15П-1Г ’Hf llL,.q.-(Rn) by Jensen inequality p 1 \ 1 г |sn-T| j f (Pa) da\< ]sn-1i j|f(pa)|pd°. Sn—1 Sn—1 Clearly, the left-hand side in (14) may be finite when the right-hand side is infinite (e. g. when f (x) = f1(p)f2(^), X = p^, |^| = 1, with f2 € L1(Sn-1), but f2 / Lp(Sn-1)). In the necessity part of Theorem 4.3 we shall use the following minimizing sequence where це(т) = r < 1, r > 1, e > 0. f _ ^(|x|) fe(X)= i in i\’ |x|pw(|x|) Lemma 4.1. Let w satisfy the condition that r5w(r) is almost decreasing for some 5 > 0. Then r [ tit). dt c J tw(t)p c^ep(r) w(r)p for all e G [0, eo], where 0 < eo <5 and c = c(eo) does not depend on e. < The proof is straightforward. > Theorem 4.3. Let 1 C p < то, 1 C q < то and w G Qq(R+). If к*(п) < то, then ||Kf||LP,q,w(Rn) C K*(n)hfllLP,q,w(Rn)- If K (|x|, |y |) ^ 0 and w satisfies the assumption of Lemma 4.1, then the condition к*(п) < то is necessary for such a boundedness; in particular, when w(r) = r-\ A > 0, the operator K is bounded if and only if ∞ У tp‘+A1K(1,t) dt < то. <1 Sufficiency of the condition к*(п) < то follows from Theorem 4.2 by Remark 4.1. To prove the necessity, we choose f (x) = fe(x). By using Lemma 4.1, it is easy to check that fe(x) G LP’q’w(Rn) for all e G (0,eo]. We have Kfe(x)= fK t1, |yD fe(|x|y)dy = / TTOVTy^T^ УИИ'Ы) d^ Rn |x| pRn |y| p w(|xHyD > |x|pw(|x|) J Rn K (1, |y|) n Ыp w*(|yD^e(|x|• Ы) dy. It is easy to check that ^e(rp) ^ ^e(r)^e(p), so that Kfe(x) > K^(n,E)fe(x), where K*(n,e) = У Rn K(1, M) n |y|p w*(|y|)^e(|y|)dy = |S”-1|( 1 p 7+C-1 ∞ K(1,p)w* Q) dp + I pp‘ e1K(1,p)w* ^p^ dp j . Hence ||K|| > K*(n,e). It remains to apply Fatou theorem when passin to the limit as e ^ 0. > In the corollary below we consider the Hardy operators H af (x) = |x|a - n / fya) dy and Hef (x) = |x^ У iffn+e dy |y|<|x| |y|>|x| and the Hilbert type operator Hf (x)= / I If ^ In dy J |x|n + |y|n Rn as examples of the operator K . Corollary 4.1. The operators Hа and He are bounded in the space Lp’q,A(Rn), 1 C p < ro, 1 C q < ro, A > 0, if and only if а < n + A and в > A - n, respectively, and a— |sn-1| II ^вц — |sn-1| and IIH II = n +A-a and IH II = n+8-x• pp The operator H is bounded in the space Lp,q,A(Rn), 1 C q < ro, A > 0, if and only if 1 C p < у and IIHI = |S^| г/A A r/1 - A A . n p′n p n < In the case of the operator Ha we have K (1,t) = | ta, t < 1, 0, t > 1, so that к*(п) = K*(n) = n , A-a. Arguments for Hв are similar. pα For the operator H we have 71 pn+A-1 K*(n) = K*(n) = |Sn-i| j 1 + tn dt, where it remains to pass the Beta function via the change 1+^ ^ t. ▻
4.2. Operator K in grand Morrey type spaces. Lemma 4.2. Let fo(x) = ixin/p^dxD and K(|x|, Ы) > 0. Then Kfo(x) > K*(n)fo(x). <1 We have ∞ lzt ( X I I n dy |Sn-1| f n-1 A dp Kf0(x) = /K(|x|, |y|) —— = , , n /Pp K(1,p) Z | h Rn |y| p w(|y|) |x| p J w(p|x|) ∞ |Sn-1| n > ---— p p' |x|pw(|x|)J 1K(1,p) inf v 1>0 w(pt) dp = K*(n)fo(x). ▻ Theorem 4.4. Let 1 C p < ro, 1 < q < ro and w E ^q(R+). If sup ^(5) У tp' 1 |K(1,t)|w* ^tA [b* ^tAj dt < ro 0<8<80 J ∞ δ for some 60 E (0, q — 1), then the operator K is bounded in the grand space Lpcqq,'w(Rn). <1 By Lemma 3.1 we take IlfII rP^.w/mn'. = sup ^(^) IlfIlLP^-^wj (Rn), Lb (R ) O<5<5o where w^(r) = w(r)[b(r)]5/q(q S). By using Theorem 4.2 and Remark 4.1, we get lKf II/P-Mon) C sup ^(^)C(5)llf^LP.q-^.wj(Rn), Lb (R ) 0<5<50 v ; where ∞ C(5) = |Sn-1| 11n-1|K(i,t)| w* (!) dt. > 0 Corollary 4.2. Let assumptions of Theorem 4.4 be satisfied and, b(r) = r^(1 + r) v, 0 < ц < v .If there exists eo > 0 such that ∞ Ko:= J^ tpeo 1|K(1,t)|w* ^t^ dt + J^ tp' ^ 1|K(1,t)|w* ^-^ dt < to, (16) then the operator K is bounded in the grand space L-’q)'™ (Rn) and < For b(r) = r^(1 + r) v, by (3) we have b> ©={ t-µ, tν-µ, t< 1, t > 1. Then it is easy to see that (16) implies (15). > Theorem 4.5. The Hardy operators Hαand H βare bounded in the grand space Lp,q),A(Rn), 1 C p < to, 1 < q < to, A > 0, with the grandizer b(r) = ([+rv, 0 < ц < v, if а < n + A and в > A — n, respectively. If ^(5) C c51/q, then these conditions are also necessary for such a boundedness. < For the operator Hа we have K£o = / tn+A-a-e0-1dt, 0 which is finite under the choice eo € (0, -n, + A — a). This ensures the boundedness of Hawhen a < pn, + A. Similarly, the sufficiency of the condition в > A — n for the boundedness of Heis checked. To prove the necessary, we choose f = fo(x) =: |x|n/P-A, so that У |fo(y)|pdy = C1rAp |y| ∞ q-δ µδ -νδ dt HfoHLp.q).A(Rn) = sup ^(8) t q (1+ t) q — b v ' «<<--! \ J t / o sup ^(5) B 0<8 µδ νδ µδ q-δ к q ’ q q ^ c sup «8<-—1 5 q ^(5) -— < TO. Thus fo E Lp,q),A(Rn). On the other hand, direct colculation shows that ∞ Hafo(x) = cfo(x), c = |Sn-1| У tn+X-a-1dt, 0 which implies that j"^ tn/p+X-a-1dt must be finite. The case of the operator Heis analogously treated. >-1
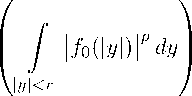
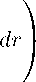
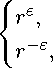
-1
Список литературы Grand Morrey type spaces
- Iwaniec, T. and Sbordone, C. On the Integrability of the Jacobian under Minimal Hypotheses, Archive for Rational Mechanics and Analysis, 1992, vol. 119, no. 2, pp. 129-143. DOI: 10.1007/BF00375119
- Fiorenza, A., Gupta, B. and Jain, P. The Maximal Theorem in Weighted Grand Lebesgue Spaces, Studia Mathematica, 2008, vol. 188, no. 2, pp. 123-133. DOI: 10.4064/sm188-2-2
- Greco, L., Iwaniec, T., and Sbordone, C. Inverting the p-Harmonic Operator, Manuscripta Mathematica, 1997, vol. 92, no. 1, pp. 249-258. DOI: 10.1007/BF02678192
- Jain, P., Singh, A. P., Singh, M. and Stepanov, V. Sawyer's Duality Principle for Grand Lebesgue Spaces, Mathematische Nachrichten, 2018, vol. 292, no. 4, pp. 841-849. DOI: 10.1002/mana.201700312
- Kokilashvili, V. and Meskhi, A. A Note on the Boundedness of the Hilbert Transform in Weighted Grand Lebesgue Spaces, Georgian Mathematical Journal, 2009, vol. 16, no. 3, pp. 547-551.
- Samko, S. G. and Umarkhadzhiev, S. M. On Iwaniec-Sbordone Spaces on Sets which May Have Infinite Measure, Azerbaijan Journal of Mathematics, 2011, vol. 1, no. 1, pp. 67-84.
- Samko, S. G. and Umarkhadzhiev, S. M. On Iwaniec-Sbordone Spaces on Sets which May Have Infinite Measure: Addendum, Azerbaijan Journal of Mathematics, 2011, vol. 1, no. 2, pp. 143-144.
- Samko, S. G. and Umarkhadzhiev, S. M. Riesz Fractional Integrals in Grand Lebesgue Spaces on Rn, Fractional Calculus and Applied Analysis, 2016, vol. 19, no. 3, pp. 608-624.
- DOI: 10.1515/fca-2016-0033
- Samko, S. G. and Umarkhadzhiev, S. M. On Grand Lebesgue Spaces on Sets of Infinite Measure, Mathematische Nachrichten, 2017, vol. 290, no. 5-6, pp. 913-919.
- DOI: 10.1002/mana.201600136
- Umarkhadzhiev, S. M. Generalization of the Notion of Grand Lebesgue Space, Russian Mathematics, 2014, vol. 58, no. 4, pp. 35-43.
- DOI: 10.3103/S1066369X14040057
- Kokilashvili, V., Meskhi, A. and Rafeiro, H. Riesz Type Potential Operators in Generalized Grand Morrey Spaces, Georgian Mathematical Journal, 2013, vol. 20, no. 1, pp. 43-64.
- DOI: 10.1515/gmj-2013-0009
- Meskhi, A. Maximal Functions, Potentials and Singular Integrals in Grand Morrey Spaces, Complex Variables and Elliptic Equations, 2011, vol. 56, no. 10-11, pp. 1003-1019.
- DOI: 10.1080/17476933.2010.534793
- Rafeiro, H. A Note on Boundedness of Operators in Grand Grand Morrey Spaces, Advances in Harmonic Analysis and Operator Theory, eds. A. Almeida, L. Castro and F.-O. Speck, Basel, Springer, 2013, vol. 229, pp. 349-356.
- DOI: 10.1007/978-3-0348-0516-2-19
- Umarkhadzhiev, S. M. The boundedness of the Riesz Potential Operator from Generalized Grand Lebesgue Spaces to Generalized Grand Morrey Spaces, Operator Theory, Operator Algebras and Applications, Basel, Birkhauser-Springer, 2014, pp. 363-373.
- DOI: 10.1007/978-3-0348-0816-3-22
- Guliyev, V. Integral Operators on Function Spaces on Homogeneous Groups and on Domains in Rn, PhD Thesis, Doctor's Degree, Moscow, Steklov Math. Inst., 1994, 329 p. (in Russian).
- Guliyev, V. Function Spaces, Integral Operators and Two Weighted Inequalities on Homogeneous Groups. Some Applications, Baku, 1999, 332 p. (in Russian).
- Adams, D. R. Lectures on Lp-Potential Theory, Umea University Reports, 1981, no. 2.
- Burenkov, V. I. and Guliyev, H. Necessary and Sufficientconditions for Boundedness of the Maximal Operator in Local Morrey-Type Spaces, Studia Mathematica, 2004, vol. 163, no. 2, pp. 157-176.
- DOI: 10.4064/sm163-2-4
- Gogatishvili, A. and Mustafayev, R. Dual Spaces of Local Morrey-Type Spaces, Czechoslovak Mathematical Journal, 2011, vol. 61, no. 3, pp. 609-622.
- DOI: 10.1007/s10587-011-0034-x
- Burenkov, V. I. Recent Progress in Studying the Boundedness of Classical Operators of Real Analysis in General Morrey-Type Spaces. I, Eurasian Mathematical Journal, 2012, vol. 3, no. 3, pp. 11-32.
- Burenkov, V. I. Recent Progress in Studying the Boundedness of Classical Operators of Real Analysis in General Morrey-Type Spaces. II, Eurasian Mathematical Journal, 2013, vol. 4, no. 1, pp. 21-45.
- Rafeiro, H., Samko, N. and Samko, S. Morrey-Campanato Spaces: an Overview, Operator Theory, Pseudo-Differential Equations, and Mathematical Physics, eds. Y. Karlovich, L. Rodino, B. Silbermann, and I. Spitkovsky, 2013, Basel, Springer, vol. 228, pp. 293-323.
- DOI: 10.1007/978-3-0348-0537-7_15
- Samko, N. G. Integral Operators Commuting with Dilations and Rotations in Generalized Morrey-Type Spaces, Mathematical Methods in the Applied Sciences, 2020, vol. 43, no. 16, pp. 9416-9434.
- DOI: 10.1002/mma.6279
- Umarkhadzhiev, S. M. Integral Operators with Homogeneous Kernels in Grand Lebesgue Spaces, Mathematical Notes, 2017, vol. 102, no. 5-6, pp. 710-721.
- DOI: 10.1134/S0001434617110104
- Kokilashvili, V. and Meskhi, A. Weighted Sobolev Inequality in Grand Mixed Norm Lebesgue Spaces, Positivity, 2020.
- DOI: 10.1007/s11117-020-00764-8


