Граница множества устойчивости одной многопараметрической системы Гамильтона

Задача гироскопической стабилизации системы осесимметричных тяжелых тел находит многочисленные применения для различных технических устройств, в частности в различных моделях центрифуг. Важной частью этой задачи является анализ устойчивости положения равновесия статически неустойчивой системы.

В работе рассматривается некоторая модельная задача, интерес к которой вызван следующими причинами. Во-первых, изначально эта задача была решена численно для двух наборов значений параметров [13] и для нее высказывалось мнение, что полного аналитического решения она не допускает. Во-вторых, в процессе решения задачи удалось не только получить аналитическое решение проблемы устойчивости в линейном приближении, но и предложить такое ее естественное обобщение, при котором более общая задача сводится к уже решенному частному случаю. В-третьих, для решения задачи были привлечены как хорошо известные методы теории исключений, так и системы компьютерной алгебры, позволяющие эффективно работать с громоздкими полиномиальными объектами. Разработаны и апробированы методы [7], реализованные в виде алгоритмов, которые, по-видимому, могут быть эффективно применены для решения целого класса задач гамильтоновой динамики.

Работа состоит из следующих разделов. В первой части формулируется задача в общей постановке, дается описание вывода уравнений движения и приводится линеаризация задачи в окрестности положения равновесия. Во второй части формулируется критерий устойчивости положения равновесия линейной системы Гамильтона и дается краткое описание методов теории исключений, применяемых в работе. В третьей части приводится вычисление множества устойчивости.

Результаты исследований докладывались на различных международных конференциях и научных семинарах. Данная статья является существенно переработанным вариантом препринта [2].

1. Постановка задачи и вывод уравнений

Рассматривается механическая система в поле силы тяжести, состоящая из осесимметричных тел, связанных между собой универсальными шарнирами Кардано — Гука (рис. 1). Центры каждого из шарниров находятся на осях симметрии соответствующих тел. Нижнее тело — невесомый стержень длиной 1 1 посредством шарнира прикреплен к оси ротора вертикально поставленного мотора, а верхний невесомый стержень длиной 1 2 жестко прикреплен к центру плоского диска массы т и диаметра d, перпендикулярно его плоскости. Ротор мотора вращается с постоянной угловой скоростью Ω (рис. 2).

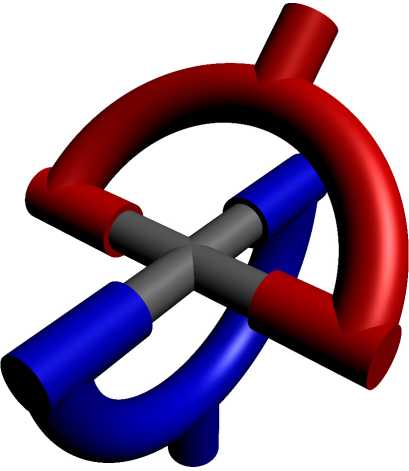
Рис. 1. Шарнир Кардано — Гука

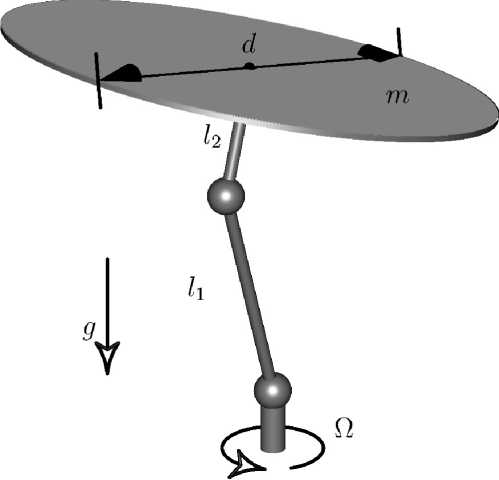
Рис. 2. Массивный диск, прикрепленный к ротору двигателя посредством упругих шарниров Кардано — Гука

Задача. Вычислить множество устойчивости для вертикального положения равновесия этой системы, то есть все те значения механических параметров системы, при которых вращение системы вблизи вертикальной оси устойчиво.

Данная задача является обобщением задачи, приведенной в [13, п. 7.8.2], где она формулировалась для фиксированных значений параметров 1 1 = 2/, 1 2 = I и d = 41 и решалась численно в линейном приближении в окрестности двух особых точек в пространстве параметров. Отметим, что сама обобщенная задача является частным случаем более общей задачи исследования устойчивости вертикального вращения статически неуравновешенной системы гироскопов Лагранжа, соединенных универсальными шарнирами Кардано — Гука (см.: [1; 5]).

В частном случае задача решена в линейном приближении аналитически с использованием методов компьютерной алгебры (базисы Гре¨бнера) и методов степенной геометрии [4]. Там же сделаны попытки исследовать более общий вариант задачи и сформулированы некоторые предположения, которые в итоге и позволили получить аналитическое решение общей задачи в линейной постановке.

В [13] приведена без вывода квадратичная часть лагранжиана частной задачи. Сделаем следующие допущения:

• •    шарниры обладают жесткостью на изгиб и кручение, силы упругости в первом приближении описываются законом Гука;

• •    массы стержней и шарниров пренебрежимо малы;

• •    углы отклонения стержней от вертикали малы;

• •    длины стержней и диаметр массивного диска произвольны;

и схематично опишем получение полного лагранжиана системы, но приведем полные формулы только для его квадратичной части.

Введем неподвижную систему координат ^тС , начало которой находится в центре 0 1 нижнего шарнира Гука, а ось С направлена вертикально вверх. Равномерно вращающуюся с угловой скоростью Q вокруг оси С систему обозначим через £ i T i C i - Систему 3 1 9 1 2 1 с началом в 0 1 и осью 2 1 , направленной вдоль стержня, свяжем с нижним стержнем. Положение системы координат 3 1 9 1 2 1 относительно вращающейся системы £ i T i £ i зададим тремя углами Крылова (иногда называемыми углами Брайнта) <р1 , 9 1 и — 1 (рис. 3).

Поскольку переход от неподвижной системы ЛК к системе 3 1 9 1 2 1 задается после- ^1.                 ^1.

довательностью поворотов ЛК —> Ч 1 Т 1 С 1 —^ 3 1 9 1 21 —> ж'1 ' 91 ' 2' 1 —> 3 1 9 1 2 1 , то вектор ш 1 угловой скорости нижнего стержня определяется по формуле

Ш1 = Лз(—К1) • ^2(—91) • (Л1 (—?1)Q + ф 1) + 01^ + ф 1, где Аг ini — матрица поворота относительно г-й оси на угол а.

Аналогично вводится система координат КТ2С2 с центром в верхнем шарнире и осями, параллельными осям системы 319121, а со вторым стержнем свяжем систему координат 329222, которая получается из системы £2т2С2 последовательными поворотами на углы ^2, 92 и -2. Тогда вектор угловой скорости ш2 массивного диска определяется по формуле ш2 = А3

^{( — 0} 2 ) • (^А 2 ^{( — 9} 2 ) • (^А 1 ( ^— ^ 2 ^{) ш} 1 + ^ф 2 ) + ⁰ 2^ + ^Z’ 2

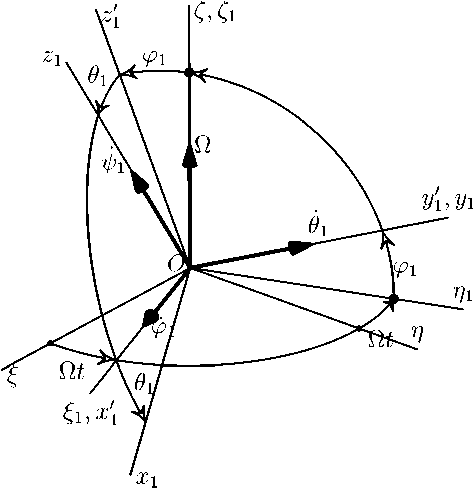
Рис. 3. Переход от неподвижной системы координат (//С к системе $ 1 ^ 1 2 1 , связанной с нижним стержнем

Положение центра масс диска в неподвижной системе координат £тС задается вектором

C = А з (nt) • Л1Ы • Л 2 (0 1 ) (/ 1 k + Л 1 (^ 2 ) • А 2 (0 2 ) • / 2 k ) .

Здесь / 1 и / 2 — длины нижнего и верхнего стержней соответственно.

Следуя [10], введем новые угловые переменные

« 1 = ^ 1 ,  3 1 = 0 1 ,  7 1 = 3 1 ,   « 2 = ^ 1 + ^ 2 ,  З 2 = 6 1 + 0 2 ,  7 2 = 3 1 + 3 2 .    (1)

Для получения функции Лагранжа L = Т — П остается записать выражения кинетической и потенциальной энергии

Т = TT ( с 2 + с, ² + с, ² ) + Л и + 7 ) + В^ш 2 , ^ у ^{2                2 ж       2} У             2 ²

П =7TigCz + Пизгиб + П кручение, в новых координатах (1), а затем разложить функцию L в ряд Тейлора и ограничиться только квадратичными по переменным at,3i,7i, г = 1,2 членами. Здесь Л и В — главные моменты инерции диска, а Пизгиб и Пкручение — потенциальная энергия сил упругости изгибных и крутильных деформаций в шарнирах.

Отметим, что получающееся таким образом выражение функции Лагранжа L мо- жет быть еще упрощено с учетом калибровочной инвариантности. В итоге имеем

^L ( ^Y , ^Y ) — — ((⁰ 2 ^- ^3 2)² + ⁽³ 2 + QQ 2 ) ² ^ +

+ | ( fi ² ( 1 - 0 2 - 3 2 ) + fi (0 2 3 2 - 0 2 3 2 ) + 7 2 ) -

+ — ^^(l 1 ⁽⁰ 1 ^{- fi}/3 1 ) + ^l 2 ⁽⁰ 2 ^{- fi}3 2 ^{)) 2} + ⁽k⁽3 1 + ^fio 1 ) + ^l 2 ⁽³ 2 + ^fio 2 ^{)) 2} ) +    (2)

^{- mg} ( ^l 2 ( 1 ^{- о} 2 /^{2 - 3} 2 /² ) + ^l 1 ( 1 ^{- о} 2 /^{2 - 3} 2 /2 )) ^-

• ^- ^ ( ^C 1 + ³ 2 ) ^- Х 2 ( ^(о 2 ^- ° 1 ^{) 2} + ⁽³ 1 ^{- 3} 2 ^{) 2} ) ^- Х 1 7 1 ^- Х 2 ⁽7 2 ^- 7 1 ^{) 2} ,

Y — (01,31,71,02,32,72), где 11 — KI, l2 — I, A — md?/4 and I — md2/2, d — 4kl, Х1,2 и Хл 2 — коэффициенты жесткости на изгиб и кручение в шарнирах.

Уравнения Эйлера — Лагранжа расщепляются на 2 подсистемы. Одна подсистема исследуется тривиально, а другая в результате замены т — fit преобразуется в гироскопическую систему с четырьмя степенями свободы М Y '' + G Y' + R Y — 0, где Y — (о 1 , 3 1 ,о ₂ ,3 2 ), Y ' — d Y / dT , М — симметричная положительно определенная матрица масс, G — кососимметричная матрица гироскопических сил, R — симметричная матрица потенциальных сил.

Преобразование Лежандра, примененное к функции Лагранжа (2), дает функцию Гамильтона Н ( Z ) в виде квадратичной формы

A —

/ R -GM ^-1 G/4 GM ^-1 /2

-M ^-1 G/2     M ^{- 1}

Матрицы, которые входят в выражение для матрицы A, имеют вид

/ A(K ² )   Д(К)             к(2К ² ) к(2К )

^М     A(K) A(^ ² +1) , ^G     к(2К )   к(2)   ,

1   А(с:

R — 7=:^

fi ²

' 1 + С 2 ^{- К} )   ^{А( -} С 2 )

^{А( -} С 2 )      ^{А( с} 2 ^- 1)

А(К ² )   А(К)

А(К) А(1 - ^ ² ) ’

А(^)-(0 0), к(^)—(0 -/),

а безразмерные параметры С 1 , с ₂ , fi выражаются l, g следующим образом:

через исходные параметры Х 1 , Х 2 , m,

Х 1

Х 2

С1 — ---7  С2 — ---р mgl       mgl

Область физических значений параметров — это положительный ортант

Ф — {с 1 > 0,   с ₂ > 0,   fi > 0, к >  0, К >  0}.

Выполним следующую замену параметров:

С 1

Р — —, fi ²

С 2             2

Т = -

,, fi ²          К fi ²

которая приведет к тому, что элементы матрицы J A в (3) станут линейными функциями от параметров р, q, г и рациональными от параметров к и К :

/ —к(1)   —к(1/К)		А((к 2 + 1)/(к 2 К 2 ))	—А(1/(к 2 К))\
⎜	А(0)      А(0)	-А(1/(к 2 К))	Л(1/к 2 )	⎟
J A —	Д(7 1 )   A(Kq/2)	-к (1)	А(0)	,          (4)
	k A(Kq/2)   Л(7 2 )	—к(1/К)	А(0)    ^
где 7 1 = К (Кг -	- р — q)/2, 7 2 = К (г —	q)/2 — к 2 .

Таким образом, вектор параметров задачи есть P = (p,q,r,k,K ). Физические значения параметров образуют область Ф : P > 0.

2. Устойчивость положения равновесия линейной системы Гамильтона

Напомним критерий устойчивости по Ляпунову положения равновесия линейной системы Гамильтоновой

^ = JA( P ) Z ,     Z = ( X , Y ) ^T , X , Y G R " ,               (5)

где J — симплектическая единица, A( P ) — вещественная постоянная симметричная матриц, элементы которой зависят от вектора вещественных параметров P G П, X — канонические координаты, а Y — сопряженные им импульсы.

Определение 1. Множество устойчивости Е системы (5) — это множество значений параметров P G П, для которых стационарное решение Z = 0 системы (5) устойчиво по Ляпунову.

Общая схема вычисления множества устойчивости положения равновесия многопараметрической гамильтоновой системы в линейном приближении дана в [4, п. 2.6]. Основная идея этой схемы заключается в том, что бо´льшая часть этапов вычисления проводится не с матрицей JA( P ), а с ее характеристическим многочленом

2 "

f(A) = f Е Л ( P )A ' ,     к = 1,                       (6)

j=0

который в силу симплектичности матрицы JA( P ) содержит только четные степени А. Поэтому в дальнейшем для вычислений используется многочлен от p = А ²

"

f G) = ЕЛ ( P )^ ' , f " = 1, f l =f 2i ,                   (7)

k=0

называемый полухарактеристическим .

Напомним критерий устойчивости положения равновесия линейной гамильтоновой системы (см., например, [14] или [4, п. 2.1]).

Теорема 1. Положение равновесия Z = 0 линейной гамильтоновой системы (5) устойчиво по Ляпунову тогда и только тогда, когда

• 1)    все корни p k полухарактеристического многочлена (7) вещественны и неположительны;

• 2)    все элементарные делители матрицы J A просты.

Граница дХ множества устойчивости состоит из частей двух гиперповерхностей в пространстве параметров

Fo = {P : /о(Р) = 0} и F2 = {P : D(/) = 0}, где D(/) — дискриминант многочлена /(^), он отличается от результанта многочленов /(д) и /‘(^) множителем (-1)т(т-1)/2 ([12, гл. xi, § 53]).

В случае рассматриваемой задачи многообразие F 0 не может являться границей множества устойчивости в силу следующего утверждения и его следствия.

Утверждение 1. Если в (3) матрицы M и R симметричные 2 х 2 -блочно-скалярные и при этом матрица М невырожденная, то определитель матрицы A есть полный квадрат, то есть принимает только неотрицательные значения.

Доказательство. Поскольку матрица A в формуле (3) 2 х 2-блочная, тогда согласно формулам Шура (см. [8, Гл. II, § 5, п. 3])

det A = det (An — A12A221A21) • det A22, где Aij — квадратные блоки матрицы A. Подставляя вместо блоков A^j соответствующие матрицы, получаем det A = det

(R

—

¹ GM ^-1 G + ¹ GM — 1 ММ ^-1 G 4           4

)

• det M ¹ = det R • det M ¹ .

Поскольку матрицы R и M 2 х 2-блочно-скалярные, то блоки R^ коммутируют между собой, а тогда из (8) следует, что detR = detR, где R = R 11 R 22 — R 12 R 21 . Но поскольку блоки R ^j есть 2 х 2-скалярные матрицы, то матрица R также будет 2 х 2-скалярной с определителем, равным квадрату диагонального элемента. Аналогичные рассуждения применимы и к матрице M , а также к обратной к ней M - 1 . Следовательно, определитель матрицы A является полным квадратом, поскольку равен произведению квадратов диагональных элементов матриц R и M - 1 , где M = M 11 M 22 — M 12 M 21 .

Следствие 1. Если матрицы R и M удовлетворяют условию утверждения 1, то критическим множеством, на котором может происходить изменение устойчивости стационарного решения системы (5) , является только множество F 2 .

Таким образом, вычисление границы множества устойчивости сводится к исследованию гиперповерхности F 2 .

Для исследования многообразия F 2 профессором А.Д. Брюно было предложено вычислить вначале ее особые точки, а затем, используя их, построить такое преобразование пространства параметров П, которое позволит упростить вид полухарактеристи-ческого многочлена /(^).

Определение 2. Пусть р(Р ) — некоторый многочлен. Точка Р = Р ⁰ множества р(Р ) = = 0 называется особой точкой к -го порядка , если в этой точке обращаются в нуль все частные производные многочлена р(Р ) по р 1 ,...,р _п до к-го порядка включительно и не обращается в нуль хотя бы одна частная производная порядка к + 1.

Отметим, что особые точки гиперповерхности F 2 связаны с кратностью корней полухарактеристического многочлена / (ц), а именно, в особых точках многочлен / (ц) имеет корни с кратностью больше 2. Это либо точки, в которых кратность корня равна 4, либо кратность корня равна 3, либо имеется пара двукратных корней. Условия кратности корней многочлена формулируются в терминах субдискриминантов многочлена /(ц). Укажем эти условия для многочлена /(ц) четвертой степени. Строгое доказательство указанной выше связи может быть проведено средствами компьютерной алгебры, но выходит за рамки данной работы. С вычислительной точки зрения использование теории исключений приводит к менее трудоемким вычислениям, чем вычисление особых точек по определению 2.

Пусть имеем многочлен четвертой степени

У^(ц) = ^ц 4 + ^/ з ^ц 3 + ^/ 2 ^ц 2 + ^ 1 ^ц + ^/ 0 ,

тогда матрица Сильвестра многочленов /(ц) и / ‘ (ц) есть
	/ 1   / 3    / 2    / 1    / 0     0    0 \ 01/ 3 / 2   / 1   / о  0 0   0    1    / 3    / 2    / 1    / о
Syl (/, / ‘ ) =	0   0    0    4    3 / з  2/ 2   / 1 0   0    4    3 / з  2/ 2   / 1    0 0   4    3 / з  2/ 2   / 1     0   0 \4   3 / з  2/ 2   / 1     0    0    0)	.                         (9)

Ее определитель равен с точностью до знака дискриминанту D(/ ) многочлена /(ц).

Определение 3. Определитель матрицы, получающийся из матрицы Сильвестра (9) вы черкиванием первых к и последних к строк и первых к и последних к столбцов (к <  4), называется к-м субдискриминантом дискриминанта D(/) и обозначается D ^{( k )} (/ ). При к = 0 имеем сам дискриминант многочлена / (ц): D ⁽⁰⁾ (/) = D(/).

Легко видеть, что к-й субдискриминант многочлена есть ни что иное как определитель к-го иннора матрицы (9) (см.: [9, гл. 1]).

Поскольку матрица Сильвестра для многочлена степени m является квадратной (2m — 1) х (2m — 1) матрицей, то такой многочлен имеет ровно m — 1 нетривиальный субдискриминант. Для матрицы (9) они равны

42    3       33   23    222

^D(/ )= ²‘J 3 J 0 + ¹⁸J 3 J 2 j 1 J 0    ⁴J 3 J 1   ^4/ 3 ^/ 2 ^/ 0 + / 3 / 2 / 1 +

+ 144/ з2М² — 6/²/ 2 / o — 8О / з / ₂ ² / 1 / о + 18 / зМ³ + 16/ ₂ 4 / o —

• — 4/ 23 / 2 — 192 / з / 1 / о² — 128/ 2 / 0 + 144 / 2 / i² / o — 27/ 4 + 256/ o³ , D ⁽¹⁾ (/) = — 6/ 3 / 1 + 2/ 2 /2 - 12 / з² / о + 2 8/ 3 / 2 / 1 — 8/ 2³ + 3 2/ 2 / 0 — 36/ 2 , D ⁽²⁾ (/) = 3/ 3 — 8/ 2 .

Теорема 2. Для того чтобы многочлен / (ц) имел d кратных корней, необходимо и достаточно, чтобы выполнялись условия:

D ⁽⁰⁾ (/) = ... = D ^{( d - 1)} (/) = 0, D ^{( d )} (/) = 0, ⏟⏞

d при этом кратные корни многочлена /(р) есть корни многочлена, который выражается через матрицу Сильвестра (9) следующим образом:

НОД (/, / ‘ ) = D (V + det Мр ) р " 1 + ••• + det М^ ,           (10)

где матрица М^ есть d -й иннор матрицы, получаемой из матрицы (9) заменой d + 1 -го справа столбца на ее же j -й справа столбец.

Доказательство этой теоремы непосредственно следует из доказательства теоремы 3.3 в [11], которая обеспечивает существование d-кратных корней двух произвольных многочленов.

Для многочлена четвертого порядка можно явно выписать условия на его коэффициенты, при которых он будет иметь либо единственный корень кратности 4, либо пару корней кратности 3 и 1, либо пару двукратных корней. Приведем эти условия здесь, поскольку они используются в дальнейших вычислениях.

Согласно теореме 2 корень кратности 4 многочлена / (р) обеспечивается условиями D ⁽⁰⁾ (/) = D ⁽¹⁾ (/) = D ⁽²⁾ (/) = 0, которые в коэффициентах многочлена / (р) записываются в виде системы

/ з⁴ - 256/ о = 0, / з³ - 16/ 1 = 0, 3/ з² - 8/ 2 = 0,                (11)

а корень кратности 4 равен р 1, ₂ , _з ,4 = -/ _з /4.

Пусть нулевой и первый субдискриминанты равны нулю (то есть d = 2), тогда многочлен (10) есть квадратный трехчлен вида

Н (р) = D ⁽²⁾ (/ )р ² + 2(/ з / 2 - 6/ 1 )р + / з / 1 - 16/ о .                (12)

Если дискриминант квадратного трехчлена (12) не равен нулю, тогда многочлен Н (р) имеет два различных корня, а многочлен /(р) имеет соответственно пару корней кратности 2. В этом случае коэффициенты многочлена /(р) удовлетворяют системе

/зз - 8/2/2 + 16/22 - 64/0 = 0, /зз - 4/з/2 + 8/1 = 0, а пара двукратных корней есть р1,2 = - (/з + yD^2)(/)^ /4, рз,4 = - ^з - ^D(2)(/)^ /4.         (13)

Если D(H) = 0, тогда многочлен Н(р) имеет один корень кратности 2, а многочлен /(р) имеет соответственно корни кратности 3 и 1. В этом случае коэффициенты многочлена /(р) удовлетворяют системе

3/з/1 - /22 - 12/о = 0, 27 [8/1 - /з (-/з2 + 4/2)]2 + D(2)(/)3 = 0, а корни суть р1,2,з = -/з/4 + \3/-2 /)з/12, р4 = -/3/4 - ^3D(2)(/)з/4.         (14)

Отметим, что условие D(2)(/) > 0 гарантирует вещественность, а при дополнительных условиях /j > 0, г = 0,1, 2, 3 и неположительность корней многочлена /(р). При условии D(2)(/) = 0 корни с различной кратностью в (13) и (14) становятся корнем кратности 4.

Наконец, если лишь D(/ ) = 0, то корень кратности 2 находится по формуле

^1,2 = - detM(1)/D(1)(/), где detM() = -9/3/о + /3/2/о + 32/з/2/о + ЗУа/2 - 4/2/1 - 48/1/о.

Два других корня многочлена / ( ц ) удовлетворяют уравнению

Ц² + ^(/ 3 + 2^ 1 , 2 )^ + / 2 + ^2/ з ^ 1 , 2 + ³^ 1 , 2 = 0.

Пункт 1) теоремы 1 для линейных гамильтоновых систем с числом степеней свободы m < 4 переформулируется в виде явных условий на коэффициенты и дискриминант полухарактеристического многочлена (7) (см. теорему 2.2 в [4]). Для случая m >  4 пункт 1) теоремы 1 конструктивно формулируется в виде условий на коэффициенты и субдискриминанты многочлена (7).

Утверждение 2. Для того чтобы все корни многочлена (7) степени m >  4 были неположительны, необходимо и достаточно выполнения условий

/ _г (Р ) >  0, г = 0,..., m - 1,      D^^f ) >  0, k = 0,..., m - 1.

3.    Вычисление множества устойчивости

Вернемся к исследованию многообразия F 2 . Дискриминант полухарактеристическо-го многочлена (7) матрицы (4) имеет вид

D(/) = /(P)4s(P)/ (4k14K9), где Z(P) = -Кг + (К + 1)q+р, а y(P) есть многочлен 5-го порядка по переменным р и q, 6-го по г и 10-го по k и К. Здесь его выражение не приводится из-за его громоздкости (многочлен содержит 976 слагаемых), но может быть легко получено из (4) с помощью любой системы компьютерной алгебры.

Для того чтобы упростить интерпретацию получаемых объектов, будем рассматривать полиномы в 3-мерном пространстве П ‘ параметров P ’ = (р, q, г), считая, что два оставшихся параметра k и К принимают фиксированные положительные значения.

Таким образом гиперповерхность F 2 в пространстве П ‘ представляет собой объединение множеств С и Q , где

С = { P ‘ : Z( P ‘ ) = 0} , Q = { P ‘ : y( P ’ ) = 0} .

Множество С — плоскость в пространстве П ‘ играет важную роль в вычислении корней кратности 3 многочлена (7), но самостоятельного интереса не представляет, поскольку, как будет показано ниже, на С множество устойчивости Х ^ лежит в множестве устойчивости Х.

В [4] показано, что структура множества Q связана с условиями кратности корней полухарактеристического многочлена / ( ц ) следующим образом:

• 1)    в особых точках 2-го порядка множества Q многочлен / (ц) имеет либо нулевой корень кратности 3, либо один ненулевой корень кратности 4;

• 2)    в особых точках 1-го порядка множества Q многочлен /(ц) имеет либо корень кратности 3, либо пару двукратных корней;

• 3)    в точках множества Q многочлен / (ц) имеет по крайней мере один корень кратности не ниже 2.

Начнем с определения параметров, при которых многочлен /(ц) имеет нулевой корень кратности 3. Свободный член / 0 полинома (7) равен определителю матрицы (4) и, в силу утверждения 1, является полным квадратом величины

К

/ оо = — --К ² г ² + К (К + 1)rq + Кгр - Kqp - 2К (К - к ² + 1)г+

+2((К + 1) ² - к²)q - 2(к ² - 1)р + 4Кк ² ) .

При фиксированных значениях параметров к и К уравнение / ₀₀ ( Р ‘ ) = 0 задает конус в пространстве параметров P ^′ с центром в точке

Р о : [ р = 2к ² , q = -2, г = -2(К - к ² + 1)/К ] .

Подставляя Р _о в многочлен /(ц), получаем корни ц 1, ₂ ,3 = 0, ц ₄ = -4.

Корень кратности 4 многочлен /(ц) имеет в особых точках 2-го порядка, а коэффициенты многочлена удовлетворяют в этом случае системе (11). Эта система имеет следующие корни:

Р 1 : [р = 0, q = 0, г = 0] ,

Г к                    1     5к ² + 2Кк + 4к + К +1 1

р2: р = 2(5к + К + 1),q = к + ^,г =---------2К--------- , р Г к                     1     5к2 - 2Кк - 4к + К +11

^р з ^: р = 2^{(5к -К -} 1) ,q = ^{-к +} ^^,г =---------2К--------- .

В точке Р 1 многочлен /(ц) имеет четырехкратный корень ц 1, ₂ ,3, ₄ = -1, а в точках Р ₂ , ₃ — четырехкратный корень ц 1 , ₂ , ₃ , ₄ = -1/4.

Отметим, что в точках Р ^ , г = 0,..., 3 собственные числа матрицы JA не зависят от параметров к и К .

Для построения упрощающего преобразования в [4] были использованы еще две особые точки — вершины двух параболических сегментов, каждый из которых есть часть однопараметрического семейства точек первого порядка.

Первый сегмент принадлежит семейству Р 1 , лежит в плоскости С и проходит через точки Р _о и Р 1 . На V 1 многочлен /(ц) имеет корень кратности 3. Параметрическое представление семейства V 1 задается формулами

' р = - к2 (t2 + 2t - 3) /2, р1 :

q = ^-

г = -

(t - 1) ² /2,

(К + к ² + 1)t ² - 2(к ² -К + 1)t + К - 3к ² + 1

2К

Вершина этой параболы есть точка при t = 0

Р 4 : [ р = 3k 2 /2, q = — 1/2, г = -(К — 3k ² + 1)/(2К) ] .

Вдоль семейства B i корни многочлена /(р) равны ^ 1 , 2 , 3 = — (t +1) 2 /4, р ₄ = — (t — 3) 2 /4.

Второй сегмент принадлежит семейству В ₂ , который проходит через точки Р ₂ и Р ₃ .

Оно вычисляется при решении системы (11) и имеет параметрическое представление

' р =k ² v ² /2 + k(K + 1)v + 2k ² ,

V 2 :

q =v ² /2 + kv,

г = — ((К + k ² + 1)v ² + 2k(K + 2k)v + 4k²) /(2К).

Вершина этой параболы есть точка при v = 0

Р 5 : [ р = 2k ² , q = 0, г = 2k ² /К ] .

Вдоль семейства В ₂ корни многочлена /(р) равны р 1 , 2(3 , 4) = (v ² — 2)/4 ± V1 — v ² /2.

Шесть найденных особых точек Р * , г = 0,..., 5 позволяют определить преобразование пространства параметров П, упрощающее многочлен /(р). Идея такой замены была высказана еще в [4, п. 3.7], но была реализована лишь частично. Эта замена переводит плоскости С и М, в которых лежат семейства B i и В ₂ соответственно, в координатные плоскости, а точку, лежащую на середине отрезка Р 4 Р 5 , переводит в начало координат новой системы. Такое преобразование имеет вид

Q = B P ’ + Р 4 Р 5 /2,

где B — матрица, столбцы которой есть векторы Р ₀ р 1 /2, Р ₂ р З /2 и Р ₄ р 5 /2:

/    k2      k(K +1)     k2/4

— 1          k1/4

k ² — К — 1 k(K + 2) k ² + К +1

\ К       К      4К/ а Q = (U, V, Ж) — вектор новых параметров. Тогда в новых переменных коэффициенты многочлена /(р) существенно упрощаются:

/ з =(5 — Ж )/2,

/ 2 = — U 2 /2 — V 2 /2 + 3Ж 2 /32 — 3U — 7Ж/16 + 43/32,

/ 1 =U ² Ж/8 + V 2 Ж/8 — Ж 3 /128 + 11U 2 /8 + UЖ/4 +

+ 3V 2 /8 — Ж 2 /128 — 5U/4 — 27Ж/128 + 29/128,

/ 00 = — U 2 /4 + V 2 /4 — Ж 2 /64 — U/2 — 3Ж/32 + 7/64, / 0 = / 00 .

Дискриминант D(/) зависит лишь от параметров (U, V, Ж), а множитель y(Q) имеет вид у (Q) = 64 U6 + 192 U 4V2 — 4 U 4Ж2 + 192 U 2V4 — 8 U 2V 2Ж 2+

+ 64 V ⁶ — 4 V ⁴ Ж ² + 72 U ⁴ Ж — 4 U ² Ж ³ — 72 V ⁴ Ж + 4 V ² Ж 3 +

+ 60 U ⁴ — 312 U ² V ² + 20 U ² Ж ² + 60 V ⁴ + 20 V ² Ж ² — Ж 4 +

+ 36 U ² Ж — 36 V ² Ж + 12 U ² + 12 V ² + 2 Ж ² — 1.

Отметим, что в новых переменных многочлен g( Q ) содержит переменные U и V только в четных степенях, следовательно он инвариантен при замене знаков у переменных U и V. Более того, если переменные U и V поменять местами, а знак переменной W заменить на противоположный, то многочлен g( Q ) не изменится. Следовательно, достаточно исследовать нули многочлена g( Q ) в одном октанте, например, для Q >  0.

Поскольку упрощающее преобразование (15) линейное невырожденное, то топологическая структура особых точек гиперповерхности F 2 остается неизменной, а независимость полухарактеристического многочлена /(^) после преобразования (15) от параметров к и К позволяет утверждать, что все результаты, полученные в новых параметрах Q , верны и для любых значений параметров к >  0, К > 0.

Множество 9 состоит из двумерной компоненты 9 и четырех одномерных компонент. Компонента 9 является линейчатой поверхностью с параметризацией

U = п sin у, V = (п + 1) cos у, W = 4п + 2 cos ² у + 1.          (16)

Образующие линейчатой поверхности 9 пересекаются с семействами Р 1 и Р ₂ только в точках параболических сегментов, заключенных между Р 0 и Р 1 для семейства Р 1 и между Р ₂ и Р 3 для семейства Р ₂ . Будем обозначать эти сегменты Р 0 и Р ° , соответственно, а их параметрическое представление задается формулами

Р_г ¹ :[V = 0, W = -2U ² - 1], -1 6 U 6 1, Р 0 :[U = 0,   W = 2V ² + 1]. - 1 6 V 6 1.

Семейство образующих имеет огибающую

У : U = — sin ³ у, V = cos ³ у, W = 3 cos2у.

При изменении параметра у образующие поверхности 9 движутся вдоль параболических сегментов Pi и Р ₂ , проходя последовательно через точки Р^ г = 0,..., 5. С учетом параметризации (16) корни полухарактеристического многочлена /(^) на поверхности 9 равны

^ 1 , 2 = —(1 + sin у) ² /4, ^ 3 , 4 = п ± (1 — sin у) V —п — cos ² у/4.

Из выражения для ^ 3 , 4 следует, что эта пара корней вещественна и отрицательна при п 6 0.

Поверхность 9 можно представить себе в виде однополостного гиперболоида с двумя склейками. Одна склейка выполнена вдоль параболического сегмента Р 0 и расположена на уровне п = — 1, другая — вдоль параболического сегмента Р 0 и расположена на уровне п = 0. Склейки повернуты на 90 ° относительно друг друга. На рисунке 4 показана линейчатая поверхность 9 вместе с семействами особых точек Р 1 , Р ₂ (сплошная линия) и У (пунктирная линия). Отмечены также особые точки Р^ г = 0,..., 5.

Линейчатая поверхность 9 делит пространство параметров Q на четыре области S _i , г = 0,1, 2, 3, в каждой из которых полухарактеристический многочлен /(^) имеет набор корней определенной структуры. Для выяснения, принадлежит ли область множеству устойчивости X, достаточно выбрать одну внутреннюю точку области и вычислить корни многочлена /(д) в ней. В областях S i , г = 1,2, 3 многочлен g( Q ) >  0, а в области S 0 многочлен g( Q ) < 0.

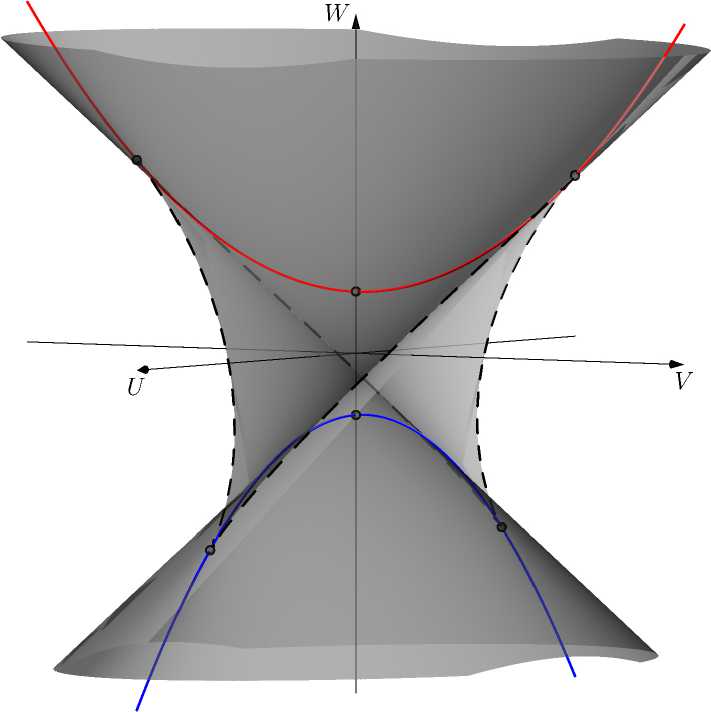
Рис. 4. Поверхность 5 с семействами Р 1 , Р 2 , У и особыми точками Р ^ , г = 0,..., 5

Область S 1 выделяется поверхностью 5 при значении и >  0 и содержит две ветви параболы Р 2 . В точках S 1 многочлен /(^) имеет две пары комплексных корней, следовательно, эта область не входит в множество устойчивости X.

Область S 2 — криволинейный тетраэдр, натянутый на сегменты Р ⁰ , Р 0 и кривую У. Его поверхность соответствует значениям параметра — 1 < и < 0. В точках области S 2 многочлен /(^) имеет вещественные корни.

Область S 3 выделяется поверхностью 5 при значении и < — 1 и содержит две ветви параболы Р 1 . В точках области S 3 многочлен /(^) имеет вещественные корни.

Область So = П‘\ (Si U S2 U S3 U 5^  — дополнение пространства параметров П‘. В точках области S0 многочлен /(^) имеет пару вещественных и пару комплексных корней, следовательно, эта область не входит в множество устойчивости X.

Непосредственная проверка показывает, что для всех точек областей S 2 и S 3 выполнены условия утверждения 2, следовательно, в этих точках многочлен /(^) имеет неположительные корни.

Осталось проверить условие 2) теоремы 1 для тех точек областей S2 и S3, в которых многочлен /(^) имеет нулевые и кратные корни. Как показано в [4, п. 2.5], для проверки простоты элементарных делителей матрицы JA достаточно вычислить ранг вспомогательной матрицы Мд(ц) = J А — л/цЕ для случаев, когда корень ц либо нулевой (тогда у исходного характеристического многочлена (6) нулевой корень имеет кратность не менее 2), либо кратный отрицательный. Здесь Е — единичная матрица.

Утверждение 3. Пусть ц — корень полухарактеристического многочлена /(ц) кратности к. Все элементарные делители матрицы JA, соответствующие этому корню, просты тогда и только тогда, когда rang Мд (ц)

( 2т — 2к, [ 2т — к,

при ц = 0, при ц <  0.

Проверка простоты элементарных делителей в точках гиперповерхностей F 0 (для случая нулевых корней) и F 2 (для случая кратных корней) дает следующее утверждение.

Утверждение 4. Матрица JA на гиперповерхности F 0 имеет простые элементарные делители всюду, кроме прямой С 1 , которая есть прямая касания гиперповерхностей

F 0 и F 2 . На границе множества устойчивости S , задаваемой частью гиперповерхности Q , элементарные делители матрицы JA непростые всюду, кроме сегмента

Р 0 .

Теперь можно сформулировать итоговое утверждение, позволяющее конструктивно описать множество устойчивости задачи.

Утверждение 5. Множество устойчивости задачи есть S ₂ U S 3 U Р ° , при этом множество S ₂ U S 3 задается системой неравенств

g( Q ) >  0, D«(f ) > 0, D^XJ ) > 0

и показано на рисунке 5.

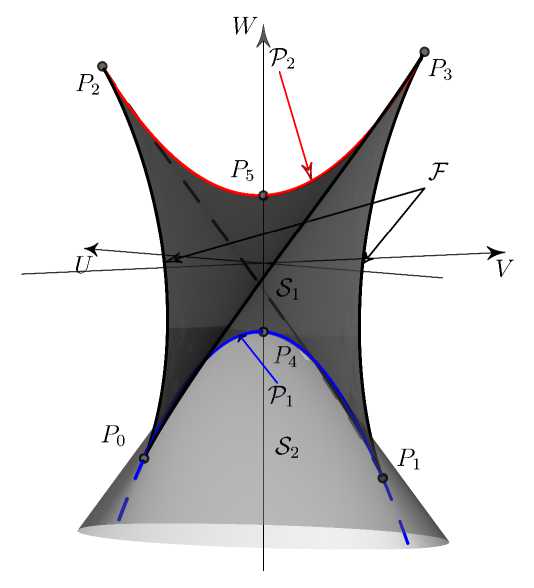
Рис. 5. Множество устойчивости в переменных ( U,V,W ) . Показаны особые точки P i , г = 0,..., 5 и семейства Р 1 , Р ₂ , F

Для физических значений параметров множество устойчивости всегда состоит:

• •    из части 5 1 в виде трехгранного клина, образованного участками сегмента 'Р2 и огибающей У ;

• •    массивной подобласти части 5 2 .

Вершина трехгранного клина — особая точка Р 2 задает наименьшее значение угловой скорости Ω вращения ротора, при котором имеется устойчивость.

Заключение

В работе рассмотрена линейная гамильтонова система, однако на самом деле исходная задача нелинейна и полное решение проблемы устойчивости положения равновесия возможно лишь с учетом нелинейных членов. В работе [3] выделена область в пространстве параметров, для которой применима теорема Лагранжа — Дирихле, но полное исследование требует вычисления нормальной формы функции Гамильтона в окрестности положения равновесия и применения соответствующих теорем о формальной устойчивости (см., например: [6; 15]).