Граничные условия для моделирования сжимаемого газа методом SPH

Достижения современных технологий в области вычислительной техники позволяют моделировать различные природные явления и решать сложные задачи в разнообразных областях науки [7]. Многие важные в теоретическом и прикладном плане процессы описываются уравнениями газодинамики.

Моделирование динамики невязкой сжимаемого газа связано с решением системы нелинейных дифференциальных уравнений [5], представленной ниже:

' dp dt du dt dE

. dt

— pdivu,

1,^

^— p V p,

— P divu, P где p — давление; p — плотность; u — вектор скорости; E — массовая плотность внутренней энергии. Система (1) замыкается уравнением состояния идеального газа: p = (7 — 1)Ep, где 7 — показатель адиабаты газа. Поскольку уравнения (1) в общем случае не имеют аналитического решения, то для их интегрирования используются различные численные методы [1].

В данной работе был использован метод сглаженных частиц (Smoothed Particles Hydrodynamics, SPH) [8]. Это бессеточный численный метод, который представляет собой мощный и достаточно универсальный подход, который часто используется для решения задач газодинамики. SPH является лагранжевым методом: он не использует какой-либо пространственной сетки для аппроксимации, что существенно упрощает численный алгоритм.

Постановка граничных условий при фиксированных пространственных границах для лагранжевых методов менее очевидна, чем в сеточных эйлеровых методах. В данной работе будет рассмотрена постановка основных типов граничных условий для метода SPH [16].

1.    Дискретизация уравнений сплошной среды1.1.    Метод сглаженных частиц (SPH)

Основная идея метода SPH состоит в дискретизации сплошной среды набором конечного числа частиц, заполняющих область Q, причем используется интегральное представление характеристик течения в виде

А(г) = j А(г )5(г — г )dr ,

Ω

где 5 — дельта-функция Дирака. Этот интеграл аппроксимируется интегралом

А(г) = J А(г )Ж (г — r,h)dr,

Ω

где Ж — весовая функция, которую называют функцией ядра сглаживания; h — длина сглаживания. Весовая функция подчиняется правилу нормировки:

I Ж( | т — т l ,h)dr = 1.

Ω

Интеграл (3) можно заменить конечной суммой по соседним относительно рассматриваемой частицам с массовым элементом pdV . Тогда для любой величины имеем:

п

A _s (r) = ^ ^i —Ж(т — т ,h), Z1    Р »

где т , , т , , р , — радиус-вектор, масса и плотность г-й частицы соответственно; п — количество частиц, соседних для г-й. Указанный переход от интегрирования к суммированию является основной идеей всего SPH-формализма.

В качестве весовой функции Ж обычно используют полиномиальные сплайны. Для задач, рассматриваемых в данной работе, используется кубический сплайн [12]

1 —

2 О ² + 4 9 3 ,  0 <  9< 1,

^{/ (} 9) = *

4 (2 — 9) 3 ,

0,

≤

≤

9 < 2,

9,

c нормировкой N (d) = { 2 ,^ ^,^ } , для d = 1, 2, 3 — размерность задачи. Это ядро удовлетворяет основным условиям, имеет непрерывную первую производную и ограничено 2h. Более гладкие ядра могут быть получены увеличением размера области и использованием сплайна более высокого порядка [9].

1.2.    Дискретные уравнения гидродинамики

C учетом описанных выше аппроксимаций (5) система уравнений гидродинамики (1) приобретает следующий вид [10]:

dE , dt

'р = £ т , (й , — й , ) V » , 3

• 1    Е т , Й + P +П./)

• 2    j    V2   р2

⁽ и , — и , ) V Ж ij ,

^dU^ = — Ет, (^^ + ^РА + П.?) V»; , , ^dt ^      V р ,     р 2

P i = (7 — 1)р , Е , .

Уравнения (7), (8), (9) являются системой обыкновенных дифференциальных уравнений.

Суммирование производится по всем соседним для г-й частицам.

Для моделирования ударных волн в SPH-методе используется искусственная вязкость. В уравнениях (8), (9) она присутствует в виде слагаемого Пу. Наиболее общая форма для искусственной вязкоcти была дана Монаганом в работе [11]:

{ - P ij aC ij + Рр 2

^U ij ^f j < ⁰ •

^U ij ^f ij ^{— 0} •

h^U ij ' ij

^РЦ = f ² + £ ² /, 2 •

где U _ij = U _i — U j , ' ij = ' — f j , а ^j , p _ij — средние значения скорости звука и плотности для частиц г и j .

Вязкое слагаемое появляется, когда частицы сжаты (то есть u _ij f _ij <  0), оно является инвариантным относительно преобразований Галилея, сохраняет полный импульс и момент импульса и исчезает в случае твердотельного вращения. Слагаемое, содержащее параметр /3 (квадратичное по u _ij ), представляет собой форму вязкости, подобную формулировке, данной в работе [15], и становится доминирующим при большой разности скоростей (то есть при больших числах Маха). Слагаемое, содержащее а (линейное по u _ij ), доминирует при маленькой разности скоростей.

1.3. Интегрирование по времени

Для численного интегрирования системы уравнений (7), (8), (9) в данной работе использовался метод Рунге — Кутты второго порядка, формулы которого приведены ниже.

U ? ⁺¹ = U ? EAt"^* ,

*     *.*

rl⁺¹ = f ? + At +±A • ** E ? ⁺¹ = Е ^¹ + At ¹ + ² .

.

Промежуточные значения в этих формулах вычисляются следующим образом:

* _ d"-? U 1 dt •	(16)
r* = u ? At,	(17)
*    dE i? E 1 = dt '	(18)
,   du ? +1 / 2 *            t	(19)
U 2        dt 1
r* = u ? +1 / 2 + At,	(20)
dE'?’+1^2 *             i	(21)
E<)                   . 2        dt

Шаг интегрирования по времени At вычисляется следующим образом:

At = К min(At 1 , At ₂ ),

где 0 <  К <  1 — безразмерное число Куранта и

△ 1 = ш1п(И _г /Й г ) 1 / 2 ,

△ 2 = ш1п(

_______________Иг_______________ с _г + 1.2ас _г + 1.2/3 шах l ^ ij |

).

2.    Постановка граничных условий для метода SPH

В большинстве научных и технических задач постановка граничных условий является неотъемлемой частью в реализации численных моделей. Физические границы расчетной области могут быть поверхностью твердых тел, ограждающих жидкость, могут быть заключены в жидкость полностью или частично. При этом сама граница может быть как стационарной, так и подвижной.

При постановке граничных условий возникают две основные проблемы. Первая проблема связана с вычислением функции ядра. Для частиц, расположенных вблизи граничной области, ядро будет усечено по границе. Так что для этих частиц W(f ij ,И) = 0. Другая проблема связана с выходом частиц за границы расчетной области: если не учесть выход частиц за границы, может возникнуть ситуация, когда все частицы расчетной области покинут ее границы. Для того чтобы это предотвратить, можно задать различные виды граничных условий: твердая стенка, периодические граничные условия, протекание и другие. В общем случае постановка граничных условий не является тривиальной задачей в методе SPH [16]. Далее будут рассмотрены некоторые способы ее решения.

2.1.    Твердая стенка

Одним из методов моделирования твердых границ в методе SPH является создание виртуальных граничных частиц. Существуют различные способы реализации виртуальных частиц. В данной работе будет рассмотрено два из них: виртуальные частицы Монагана [11] и частицы Морриса [13]. Наглядная визуализация их представлена на рисунке 1, граничные виртуальные частицы изображены более темным цветом.

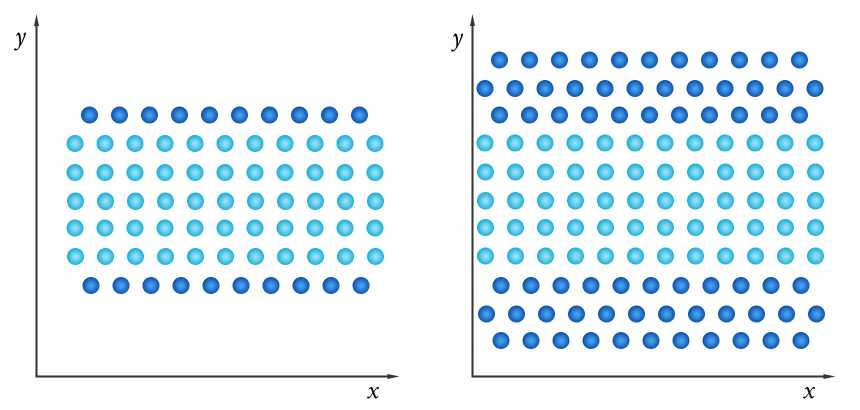
Рис. 1. Модель расположения виртуальных частиц Монагана (слева) и частиц Морриса (справа)

Частицы Монагана представляют собой виртульные частицы, расположенные прямо на границе расчетной области в один слой. Они обладают всеми характеристиками

SPH-частиц (массой, давлением, плотностью, энергией), но при этом не меняют своих параметров и участвуют в расчете только в качестве соседних частиц. При этом между частицами, находящимися вблизи границ, и виртуальными задается некоторый потенциал взаимодействия. Сила отталкивания не позволяет частицам покидать расчетную область и решает проблему отсутствия достаточного числа соседних частиц на границах, и, как следствие, усечения ядра сглаживания. Для этого Монаганом был предложен потенциал Леннарда-Джонса [3]:

i W D |( 7 Г - ( 7 0 ) 6 ] , (25)

где D — глубина потенциальной ямы, зависящая от условий конкретной задачи; г о — расстояние, на котором обращается в ноль потенциал взаимодействия. Сила отталкивания возникает только при выполнении условия г < г ₀ .

Другой подход к постановке граничных условий был предложен Моррисом и соав-тороми [13]. Суть подхода заключается в создании виртуальных частиц вне расчетной области. Изначально эти частицы расставляются в строгом порядке в несколько слоев. Они всегда остаются в своем начальном положении и имеют нулевую скорость.

Центры первого слоя граничных частиц лежат непосредственно на границе виртуальных частиц и частиц газа, гарантируя нулевую скорость на границе. Виртуальные частицы не перемещаются, но при этом могут оказывать давление на частицы, расположенные на границах. В отличие от частиц Монагана, эти частицы участвуют в расчете и могут менять свои характеристики с течением времени. В данном случае задавать потенциал взаимодействия не требуется.

Преимущество этого метода заключается в том, что при задании границ таким образом сохраняется возможность распараллеливания расчетов как для частиц газа, так и для виртуальных частиц, поскольку вычисление характеристик виртуальных частиц аналогично расчету характеристик частиц газа, за исключением того, что виртуальные частицы не меняют с течением времени своих координат.

Недостаток применения частиц Морриса состоит в том, что для описания границ необходимо дополнительно вводить в расчет довольно большое количество виртуальных частиц, что приводит к замедлению расчета.

2.2.    Протекание

Задача протекания жидкости сквозь заданную область возникает, когда скорость жидкости не равна нулю. Для ее корректной постановки (в отличие от задачи о течении в замкнутой области) требуется граничное условие, которое задает параметры втекающего в расчетную область газа в каждый момент времени t.

Принципиальная схема реализации протекания приведена на рисунке 2. Представленный способ требует, чтобы граница была плоской, и, кроме того, чтобы поток был нормальным (перпендикулярным) к границе (на практике это может быть достигнуто путем размещения входной границы достаточно далеко от любых особенностей течения, которые могут вызвать неоднонаправленный поток).

Каждый раз, когда частица пересекает границу расчетной области, новая частица создается и появляется выше по потоку. Этот подход обеспечивает необходимую плотность частиц на входной границе. Обновление параметров частиц внутри зоны притока зависит от аналитического граничного условия, которое определяется при постановке задачи.

Выходную границу проще реализовать, так как никакие новые частицы не созда- ются. При пересечении границы частицы прекращают участвовать в расчетах.

Зона притока-

Зона течения----

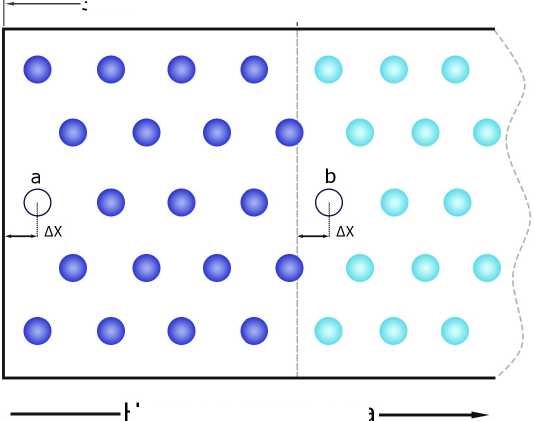
Направление потока

Рис. 2. Принципиальная схема зоны притока через границу. Новая частица добавляется, когда

существующая частица b переходит из области входа в расчетную область

г г г г с г г г г г г г г с г г г г г г х' г г г х' х' х' х' х'

х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х'

••ее                       •••

•••••                     ••••

••ее                          .'.'.'•••

•ее-                            ее х' X* X* х' х' х' х' х' х' х' г х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х'

х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х' х'

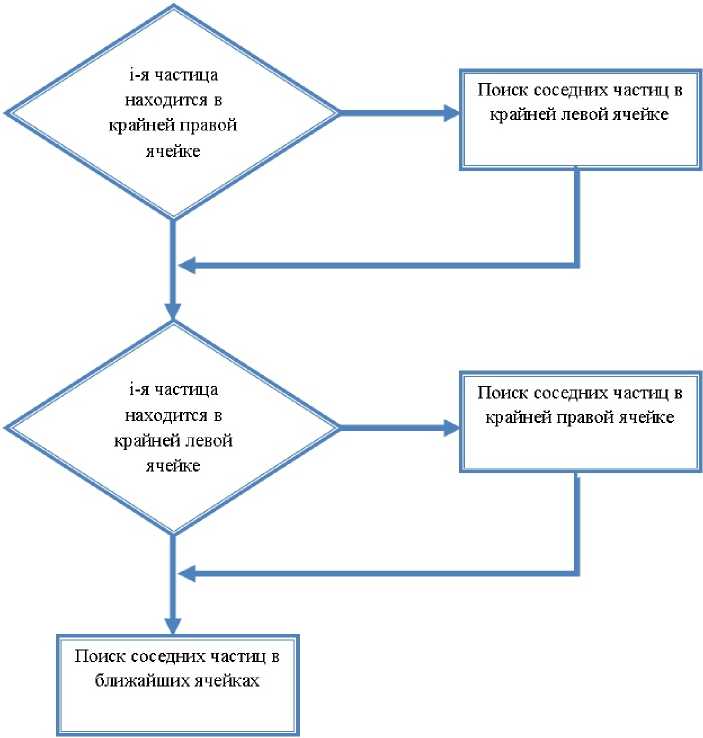
Рис. 3. Схема модифицированного алгоритма поиска

Рис. 4. Распределение соседних частиц для частицы на границе

соседних частиц

Если граничные условия таковы, что вход через одну границу равен выходу через другую и параметры жидкости на границах равны, то можно использовать следующий подход. Когда частица выходит за границу расчетной области, она возвращается на противоположную границу с начальными параметрами задачи: фактически создается новая частица взамен вышедшей за границу.

Для реализации данных граничных условий алгоритм поиска соседних частиц, основанный на списках и описанный в отчете по НИР (А.С. Васюра «Реализация граничных условий для метода Smoothed Particle Hydrodynamics», 2013 г.), требует важных изменений. Кроме частиц, находящихся в области радиуса 2^, для граничных частиц соседними будут являться частицы, находящиеся в области границ на противоположной стороне расчетной области, для которых выполняется условие

I X i

^x wall | + ^lx j    ^x wall | <  2h,

где X i — координата г-й частицы; x _wall — координата границы.

В соответствии с алгоритмом поиска, основанном на списках, расчетная область разбивается на ячейки размером 2^. Для частиц, находящихся в крайней правой или в крайней левой ячейке, требуется реализовать поиск по частицам в противоположной ячейке, на выполнение условия (26). На рисунке 3 представлена схема выполнения преобразованного поиска соседних частиц.

На рисунке 4 показаны соседние для крайней левой ячейки частицы.

3.    Граница между веществом и вакуумом

Для большинства эйлеровых схем постановка граничных условий вещество — вакуум является весьма нетривиальной и сопряжена с рядом сложностей при реализации. Одним из достоинств метода SPH является простота и естественность при постановке таких граничных условий. Это можно наблюдать, например, при моделировании динамики газового галактического диска во внешнем потенциале других компонент галактики [6].

В качестве потенциала используется модель квазиизотермического гало [4]:

^М)   (1 + ( 2 /а 2 ) ^к

Плотность вещества в диске распределена согласно следующему закону:

( А             1

Р(П = --ГТГГ cosh( )

Согласно этому плотность убывает от центра к периферии диска (см.: рис. 5). Следственно, уменьшается и число взаимодействующих частиц, как показано на рисунке 6. Поэтому SPH-алгоритм не требует дополнительной реализации граничных условий и при этом дает корректный результат.

4.    Тестирование

Для тестирования способов постановки граничных условий используется стандартная задача для схем, моделирующих сжимаемый газ: задача о распаде произвольного Р 1

разрыва. На рисунке 7 представлено начальное распределение давления, где — = 10 — скачок давления, плотность р = 1. Скорость в начальный момент времени равна нулю U = 0, 7 = - — показатель адиабаты.

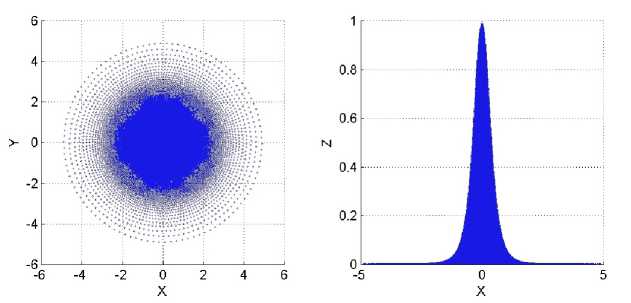
Рис. 5. Начальное распределение плотности. Справа вид сверху, слева вид сбоку

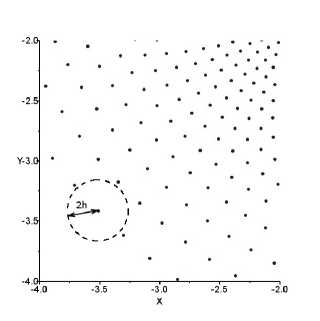
Рис. 6. Положение частиц на границе диска. Окружность показывает область взаимодействия частицы с

соседними

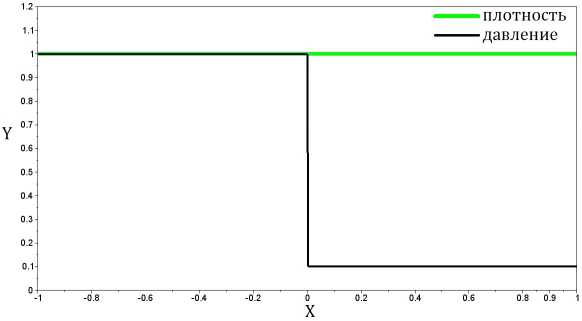
Рис. 7. Начальные распределения давления и плотности в задаче о распаде произвольного разрыва

Для сравнения использовалось точное решение газодинамической задачи Римана [2], состоящее из элементарных решений (ударная волна, волна разрежения, контактный разрыв), которые отделены друг от друга областями с постоянными значениями параметров.

На рисунках 8–9 изображены распределения плотности, давления и скорости в момент времени t = 0.3. Расчеты были произведены для количества частиц N = = 200,1000, 30 000. Можно видеть, что точность решения сильно зависит от количества частиц. С увеличением количества частиц наблюдается сходимость к точному решению.

Для численного интегрирования использовалась описанная ранее схема метода Рунге — Кутты. При вычислении гидродинамических параметров для рассматриваемой г-й частицы необходимо знать, какие частицы являются ее «соседками», для этого используется алгоритм поиска соседей.

Чем больше число частиц N , тем выше точность решения, что наглядно отражено на рисунках 8-9. Корректный выбор N и длины сглаживания h позволяет добиться наиболее точного результата.

На рисунке 10 (слева) представлено решение задачи Римана со свободной границей в различные моменты времени. Для реализации свободной границы требуется учесть только особенный расчет градиента для частиц в области границ. По графику можно увидеть, что со временем все частицы выходят за пределы расчетной области. Чтобы этого избежать, требуется задание граничных условий, таких как твердая стенка или протекание.

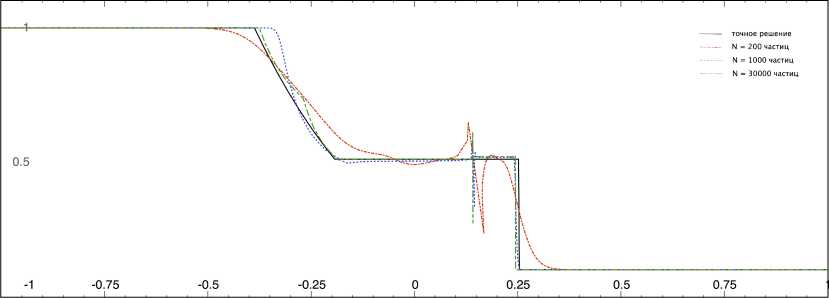
Рис. 8. Зависимость давления от координаты в момент времени t = 0 . 3 , количество частиц N = 200 , 1000 , 30 000

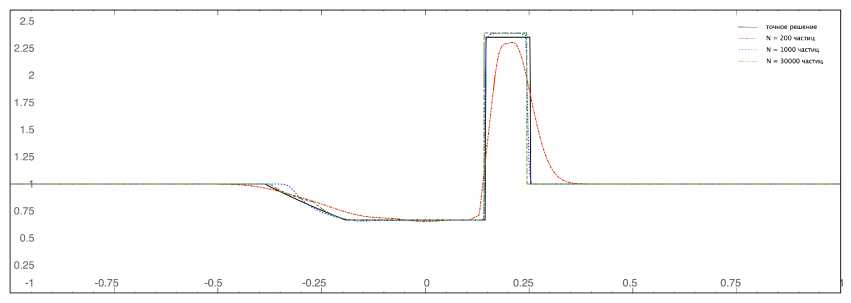
Рис. 9. Зависимость плотности от координаты в момент времени t = 0 . 3 , количество частиц N = 200 , 1000 , 30 000

На рисунке 11 изображено решение задачи Римана, где в качестве граничных условий была задана твердая стенка. Данное граничное условие предполагает, что активные частицы не могут выйти за пределы расчетной области.

На рисунке 12 можно увидеть положение частиц в различные моменты времени. Когда волна доходит до правой границы расчетной области, плотность частиц сильно увеличивается, и зафиксированные частицы Морриса не дают частицам газа выйти за пределы границ, поэтому волна меняет свое направление на противоположное.

Заключение

В данной работе были рассмотрены основные виды граничных условий. Несмотря на то что сам SPH-метод является универсальным для широкого круга задач, постановка граничных условий требует индивидуальной реализации в зависимости от поставленной задачи. Один и тот же вид граничных условий для метода SPH может быть реализован по-разному.

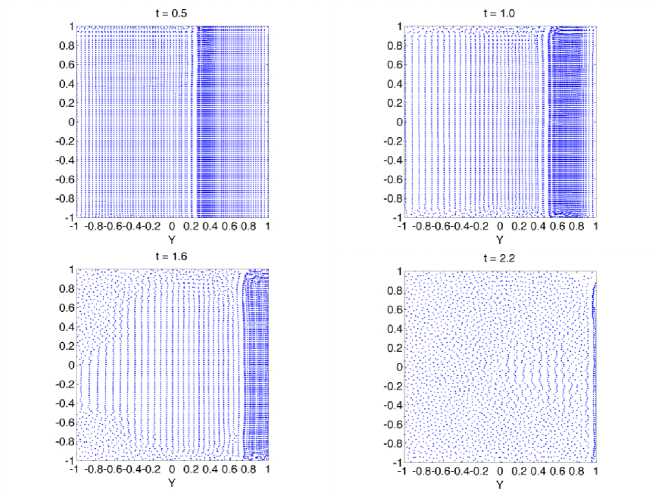
Рис. 10. Положение частиц в моменты времени t = 0 . 5 , 1 . 0 , 1 . 6 , 2 . 2

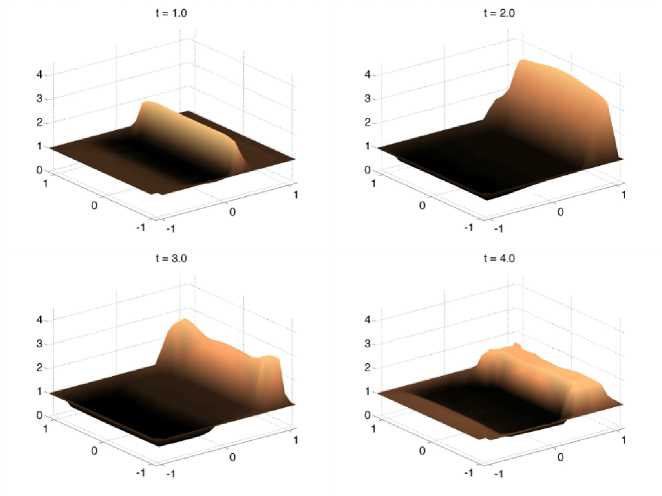
Рис. 11. Распределение плотности частиц в моменты времени t = 1.0, 2.0, 3.0,4.0

Например, для задания твердой стенки можно использовать частицы Монагана или частицы Морриса. От выбора способа реализации граничных условий напрямую зависит точность результатов вычислений.

С другой стороны, одним из достоинств метода SPH является естественность расчетов границы вещество — вакуум. В таких случаях, с учетом особенностей этого метода, дополнительная реализация граничных условий не требуется, в то время как для альтернативных сеточных методов постановка границ вещество — вакуум требует дополнительных нетривиальных вычислений и регуляризации.

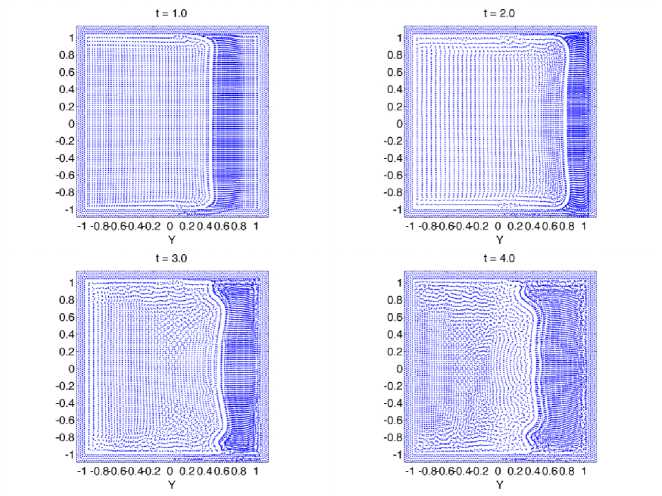
Рис. 12. Распределение частиц в моменты времени t = 1 . 0 , 2 . 0 , 3 . 0 , 4 . 0