Граничные условия при конвективной сушке рыбы

Процесс сушки является одним из основных этапов в технологии приготовления копченой и вяленой рыбопродукции. Факторы, влияющие на внутренний массоперенос в рыбе и внешний массоперенос от рыбы к сушильному агенту, в значительной степени воздействуют на продолжительность процесса и его энергоемкость, а также определяют органолептические показатели готовой продукции и сроки ее хранения. Тепловые расчеты сушильных установок обычно сводятся к определению расхода тепла на сушку при значениях параметра сушильного агента, рекомендуемых технологическими инструкциями. При этом не учитываются закономерности переноса влаги между рыбой и сушильным агентом. Рабочим агентом в сушильной камере является смесь сухого воздуха и водяного пара, доля которого в смеси характеризуется величиной его парциального давления. При этом парциальное давление пара в пограничном слое около влажного материала всегда больше, чем в основной массе воздуха. Под действием разности этих давлений происходит диффузия пара от материала в воздух. При прочих равных условиях скорость выделения пара с поверхности материала зависит от парциального давления пара в воздухе или от его влагосодержания Х . Процесс сушки рыбы прекращается при граничных условиях, когда влажность материала достигает значения равновесной влажности. Изотермы десорбции влаги зависят от химического состава, состояния материала и устанавливаются только экспериментальным путем.

Описание экспериментальной установки и методики проведения опытов

Для исследования равновесного состояния рыбы и потока воздуха были проведены экспериментальные исследования равновесной влажности салаки в потоке воздуха с заданными параметрами.

Равновесную влажность целой неразделанной салаки определяли в потоке воздуха, движущегося со средней скоростью 1,2 м/с при температуре +30 ° С. Относительная влажность воздуха регулировалась от 85 до 30 %. Влажность рыбы определяли по методике, указанной в ГОСТ 13930.

Исследования по определению равновесной влажности рыбы в потоке воздуха для оптимизации параметров воздуха в процессе сушки при вялении и холодном копчении проводились на экспериментальной установке, позволяющей поддерживать в течение длительного времени постоянные параметры воздуха: температуру, относительную влажность и скорость. Схема установки представлена на рис. 1 [1].

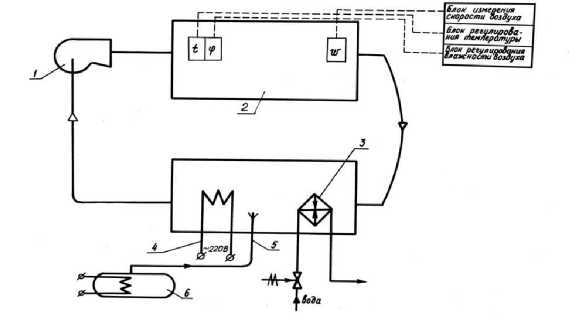
Рис. 1. Схема экспериментальной установки: 1 – вентилятор; 2 – сушильная камера;

3 – воздухоохладитель; 4 – электрический воздухонагреватель; 5 – увлажнитель; 6 – парогенератор

Результаты исследования и их обсуждение

Дифференциальное уравнение влагопереноса рыбы для условий проведенных опытов может быть записано в следующем виде [2], [3]:

9U 9 ( 19U )

----=---- A ---- ,                                             (1)

9t 9 X ( 9 X )

где t – время; X – координата; U = U ( X , t ) – влагосодержание; А – коэффициент влагопереноса.

Краевые условия к дифференциальному уравнению (1):

(

U ( X ,0) = / ( X ) , I — I = 0 , A l — I   =- J ,                     (2)

I5 X )x=0        I-X ) X=L где J – интенсивность поверхностного влагообмена.

В периоде падающей скорости для решения задач на нахождение поля влагосодержания была предложена формула для влагообмена между поверхностью тела и окружающей средой [2]:

J = a(u(L, t) - Up),                                          (3)

где α – коэффициент влагообмена, отнесенный к разнице влагосодержаний; U р – на равновесное влагосодержание.

Формула (3), конечно, не применима к периоду постоянной скорости сушки, так как для J = const коэффициент α будет непрерывно увеличиваться с уменьшением влагосодержания, потому что влагосодержание поверхности тела U ( L , t ) уменьшается в процессе сушки.

Дифференциальное уравнение влагопереноса (1) при краевых условиях (2) при допущении, что массообменные характеристики А и α не изменяются, было аналитически решено А. В. Лыковым [2]. Но коэффициент влагопереноса рыбы А зависит от влагосодержания, его нельзя выносить из-под знака производной в уравнении (1). Можно использовать эмпирическую формулу [4]:

A ( U ) = A p + K ( U - U p ) .

Введем безразмерные величины:

u =

U - U p U - U p

X x = _L ,

tAp       A т = ——, a = — = 1 + ku ,

L ²        A p

k = K

U 0

-

U p

A p

Из равенств (4) выразим размерные величины и подставим в формулы (1) и (2). После преобразования получим дифференциальное уравнение влагопереноса и краевые условия в безразмерной форме:

9 u 9(9 u — = —I a — 9 т 9 x I 9 x

u ( x , 0) = 1 , | Ё Ц. I 9 x

|     = 0, x=0

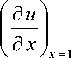
= -Biu (1, t ) ,

где массообменное число Био

Bi = aL / A p .

Краевая задача (5), (6) не может быть решена аналитически, так как коэффициент массопереноса является функцией влагосодержания. Для численного решения задачи в среде Mathcad введем безразмерную величину градиента влагопереноса q и преобразуем (5), (6) к виду d u 9 q       d u

— = —, q = a—, 5т 5x       5x

u( x,0) = 1 , q (0, т ) = 0 , q (1, t) = - Bi u (1, t) .

Для решения поставленной краевой задачи необходимо найти параметры конкретного образца рыбы. На рис. 2 представлена экспериментально полученная зависимость равновесного влагосодержания салаки при 30 °С от относительной влажности подаваемого воздуха [1].

Методом наименьших квадратов в среде Mathcad [4] было установлено, что наименьшее среднее квадратическое отклонение ε получается при аппроксимации зависимости многочленом 2-го порядка:

R 2 ( ф ) = 0,198 - 0,354 ф + 2,340 ф ² .

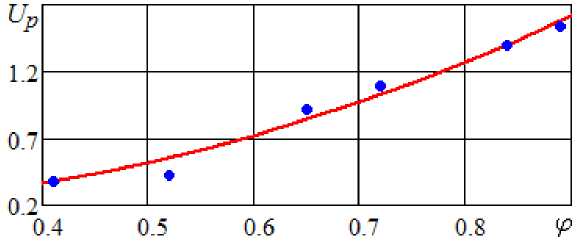
Рис. 2. Зависимость равновесного влагосодержания салаки (кг влаги на кг сухого вещества) от относительной влажности воздуха при 30 °С.

Точки – опытные данные; линия – расчет по формуле (7)

Величина отклонения рассчитана по формуле [5]

е

n

= 100

1 ^N ( и А А —— У| 1 - ' I N N - n - 1 ⁶ ( R ( Ф , ) J

где N - объем выборки; R „ - многочлен аппроксимации n -го порядка; ( ф , , U _р ) - экспериментальные точки, и представлена в таблице.

Параметры аппроксимации

Порядок многочлена аппроксимации n	1	2	3
Среднее квадратическое отклонение ε, %	44,6	14,6	16,0

Покажем, как можно оценить величину коэффициента влагообмена α по экспериментальным данным. В периоде постоянной скорости сушки

---= Q = const. d1

Проинтегрируем обе части уравнения (1) по толщине слоя L :

[QdX = - [—(A—) dX, 0        l J0 a x ( a x J

.

X=L

Из формулы (8) с учетом граничных условий (2), (3) можно получить

a( t ) =

QL

U ( L, t ) - U p .

Величина U ( L , t ) уменьшается, а так как Q = const; из уравнения (9) следует известный факт [2]: a ( t ) возрастает в период постоянной скорости сушки.

Исходя из принятой модели, в период падающей скорости сушки α = const. Тогда это постоянное значение можно оценить в граничной точке между указанными периодами сушки по формуле

α≈

∂W L ∂t

W -Wp где W – среднее влагосодержание образца рыбы, определенное в экспериментах [5], [6]. Оно связано с локальным влагосодержанием формулой

L

w ( t ) = - Ju ( x , t ) dx .

L 0

На рис. 3–12 представлены результаты расчетов при k = 0,1 и различных значениях числа Био массообмена.

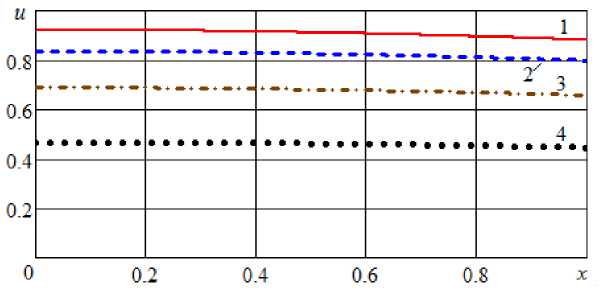
Рис. 3. Профили безразмерного влагосодержания при Bi = 0,1 и различном безразмерном времени: 1 – τ = 1; 2 – τ = 2; 4 – τ = 4; 1 – τ = 8

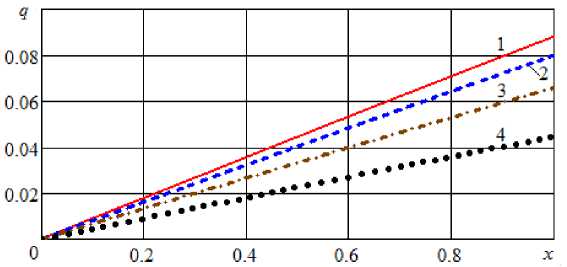
Рис. 4. Профили безразмерного модуля градиента влагосодержания при Bi = 0,1 и различных значениях τ: 1 – τ = 1; 2 – τ = 2; 4 – τ = 4; 1 – τ = 8

Рис. 5. Профили безразмерного влагосодержания при Bi = 0,3 и различном безразмерном времени: 1 – τ = 1; 2 – τ = 2; 4 – τ = 4; 1 – τ = 8

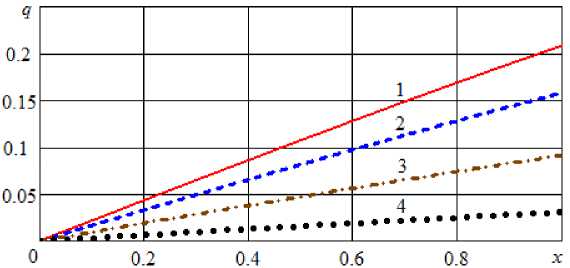
Рис. 6. Профили безразмерного модуля градиента влагосодержания при Bi = 0,3 и различных значениях τ: 1 – τ = 1; 2 – τ = 2; 4 – τ = 4; 1 – τ = 8

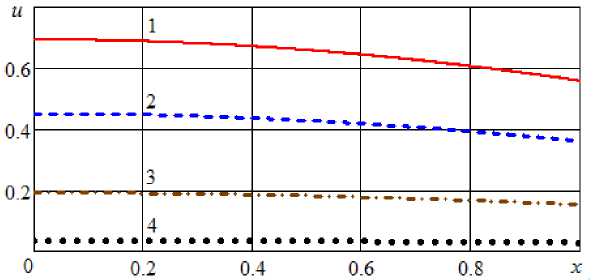
Рис. 7. Профили безразмерного влагосодержания при Bi = 0,5 и различном безразмерном времени: 1 – τ = 1; 2 – τ = 2; 4 – τ = 4; 1 – τ = 8

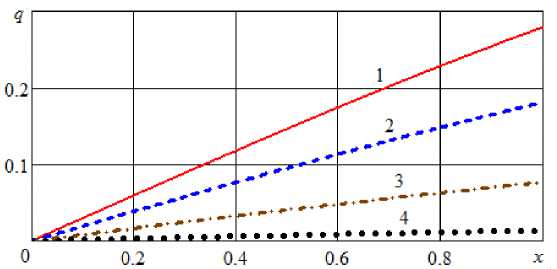
Рис. 8. Профили безразмерного модуля градиента влагосодержания при Bi = 0,5 и различных значениях τ: 1 – τ = 1; 2 – τ = 2; 4 – τ = 4; 1 – τ = 8

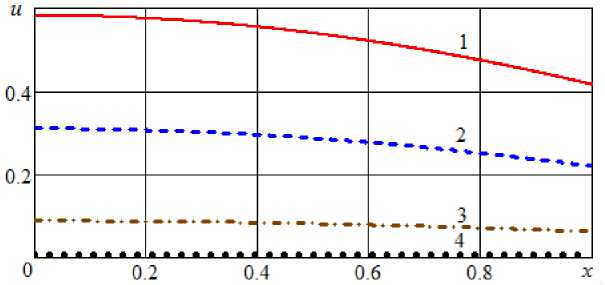
Рис. 9. Профили безразмерного влагосодержания при Bi = 0,8 и различном безразмерном времени: 1 – τ = 1; 2 – τ = 2; 4 – τ = 4; 1 – τ = 8

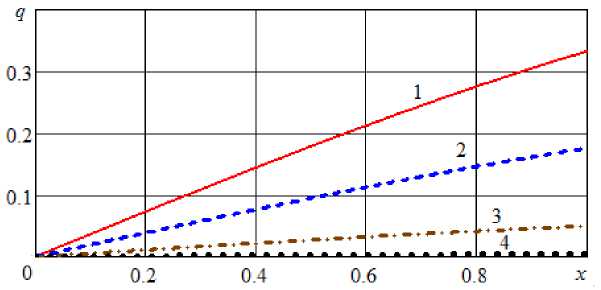
Рис. 10. Профили безразмерного модуля градиента влагосодержания при Bi = 0,8 и различных значениях τ: 1 – τ = 1; 2 – τ = 2; 4 – τ = 4; 1 – τ = 8

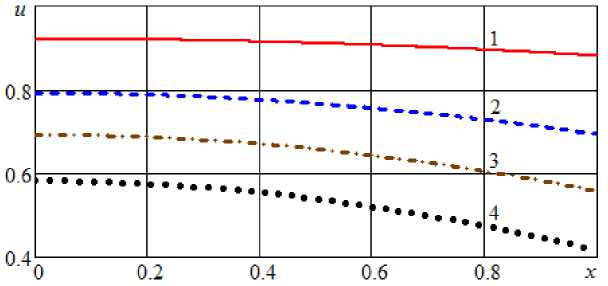
Рис. 11. Профили безразмерного влагосодержания при τ = 1 и различных значениях числа Био: 1 – Bi = 0,1; 2 – Bi = 0,3; 4 – Bi = 0,5; 1 – Bi = 0,8

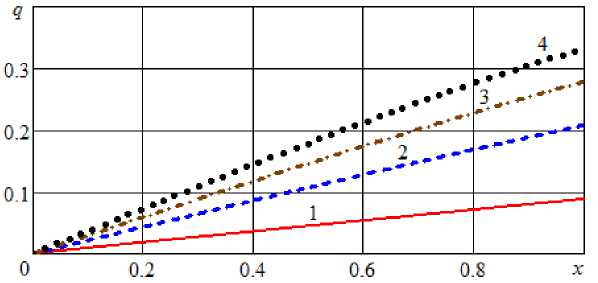
Рис. 12. Профили безразмерного модуля градиента влагосодержания при τ = 1 и различных значениях Bi : 1 – Bi = 0,1; 2 – Bi = 0,3; 4 – Bi = 0,5; 1 – Bi = 0,8

Заключение

Получены экспериментальные данные равновесной влажности целой неразделанной салаки, которые аппроксимированы многочленом 2-го порядка.

Составлено дифференциальное уравнение влагопереноса и краевые условия, выраженные в безразмерной форме.