Graph Models for Knowledge Representation and Reasoning for Contemporary and Emerging Needs – A Survey

Published Online February 2016 in MECS DOI: 10.5815/ijitcs.2016.02.02

Knowledge representation and reasoning is crucial for performing intelligent processing of data, especially if data to be processed is voluminous and complex. The ability to reason out a solution to any given real world problem depends on knowledge available in the domain. Contemporary Data Intensive Systems with emergence of Big Data, require intelligent processing of data which in turn depends on solid underlying knowledge representation and reasoning used in interpretation and analysis tasks in such systems [1]. A reasonably complex data intensive system usually has to represent concepts within or across domains, and has good affinity to logic to reason and predict. Information collected in any domain should be represented in proper form for reasoning to be performed. Practical reasoning systems can be designed only if the knowledge representation is in a form suitable for the reasoning approach in any system. Hence most reasoning systems prescribe the knowledge representation needed for their specific reasoning methods to work.

Graph based models work well for representation and reasoning. Several methods such as using Conceptual Graphs for representation and logic for reasoning [2] [3] [4], semantic networks for knowledge representation on which first order logic can be applied for an end-to-end effective Knowledge Representation and Reasoning (KRR) system[5], Inference graphs [6] [7], and probabilistic Causal Bayesian Network [8] [9] and Concept graphs [10] [11] exist.

This paper does a detailed survey of popular graph models used in contemporary scenarios, with the motivation of providing a comparative study of these models so that a practitioner can choose a suitable knowledge representation and reasoning model in real world applications. In the following sections we discuss about knowledge based systems with various graph models for KRR, recent usage of each model in voluminous data and complex relationships scenario, and needs and challenges in immediate future.

• II.    Related Work

All knowledge based systems feature a knowledge base which holds information and an associated reasoning system which is used in processing the information. Each system allows defining domain ontology with concepts/entities, a classification mechanism for concepts, properties and relationships. Also they typically define the scope of reasoning systems within a subset of logic [12]. A computationally feasible knowledge representation usually involves capacity to define and operate on entities (concepts) and relationships among them in a specific application domain. For example the most famous protégé tool for OWL (Web Ontology language) allows semantic representation and uses reasoning modules such as Fact++ and HermiT OWL Reasoner which use Description Logic for reasoning [13] [14] [15]. Their typical use is for generating implicit relationships and properties among defined concepts using reasoning.

A reasoning module may attempt to provide answers for queries posed in an application domain specific KRR, using the knowledge available in the domain, defined through the ontological vocabulary. During such attempts, the reasoning module may explicitly bring out implicit relationships, effectively resulting in generation of new ontologically representable knowledge within the concerned application domain [12]. This also implies that if the application domain knowledge is updated through means other than the reasoning module, than the reasoning module will have to be run again to evaluate current knowledge. This can become costly in data intensive environments.

Considering complex and data intensive systems where data is tending to become Big Data with high volume, velocity and variety, it is mandatory for KRR to perform within the posed time limits. For such scenarios Artificial Intelligence and Machine Learning techniques can be used during analysis for concepts extensions [5] [46]. A high expressive power may be desired but it may result in higher computing cost based on the type of logic used. Hence usually there has to be a tradeoff between these two [5]. Most contemporary systems use subsets of First Order Logic (FOL) for reasoning. However FOL based systems will not be able to handle domains with infinite members and hence range of variables within considered candidate domain should be finite for FOL to be used for reasoning [12] [16].

From the above it can be seen that for any sound KRR system, necessary capabilities are vocabulary with semantic notations, logic and reasoning foundation, a balance between computability and expressivity to be used in real world knowledge based systems, and features to extend knowledge using existing knowledge premises and conclusions [12] [17].

Knowledge representation based on graphs provides the advantages of graphical models in terms of readability, visual clarity and computational viability. It is easier for humans to validate graph based representation and reasoning. Graphs can be understood by the subject matter experts who may not have familiarity with other forms of formalisms. Reasoning in graph based knowledge systems, for the most part, can be done with basic and extended graph features themselves. Recent increase in representation through graphs in knowledge based systems further strengthens the given arguments [12] [18] [45] [46].

From the above related work, it is clear that when building real world applications using KRR, a crucial part of solution is to choose appropriate KRR system. This survey provides not only a review of popular graph models, but also gives a comparative study of them using important and relevant factors for building solutions. Of several possible candidate graph models, this survey focuses on conceptual graphs, Concept graphs, Causal Bayesian networks, Semantic networks, and Inference graphs. Overviews for each type are provided along with recent applications dealing with voluminous data. The survey results are presented in a table comparing the models with one another on knowledge representation, reasoning, usage in data intensive scenarios and tool support.

• III.    Conceptual Graphs

Conceptual graphs attempt to combine the expressiveness of natural languages and preciseness of logic formalisms. They provide a model which can be described well using theory and can be combined with strong logic. They can be also viewed as data structures which can be implemented with reasonable ease, which can be very useful in building AI systems solving complex problems[19]. The term ‘Conceptual Graph’ actually represents a set of formalisms originated by John Sowa[18]. There are different types of conceptual graphs such as Basic Conceptual Graphs (BG), Simple Conceptual Graphs (SG), and Positive Nested Conceptual Graphs[12]. There are several tools which help in drawing conceptual graphs and reasoning with them. CharGer, CG Mars Lander, CoGITaNT, CPE, GoGui and Prolog+CG are some of the widely used tools[20]. Software such as Amine[21], Cogitant[22] and Notio[23] are available as programming API platforms.

The vocabulary of conceptual graphs is divided into two sets: a set of concepts (also known as classes or concept types) and a set of relations. A concept or a class is an entity within a specific domain. Concept types can have hierarchical generalization/ specialization relationships with one another. The set of relations may contain symbols denoting the relations. Relations or relation types connect different entities with one another in a conceptual graph. Hence both the sets of concepts and relations are partially ordered sets. In a conceptual graph nodes can be either concepts or relations. Each node is labeled to show if it is a concept or a relation, and a node may be marked with an individual marker to refer to a specific entity, followed by the type. Total ordering, showing the intended sequence of the concept-relation edges can be achieved with numeric labels alongside edges. Conceptual graphs were developed from the existential graphs, so the presence of a relationship between two concepts implies that it is an assertion [3] [12] [19].

For example, consider the statement ‘if the student reads the book, then the student gains knowledge’. This can be represented in a CG as shown in Figure 1. The ‘Then’ clause is shown in a inner box, whereas the Student and Reader concepts are connected by a conference link, denoting that both are the same entities [24].

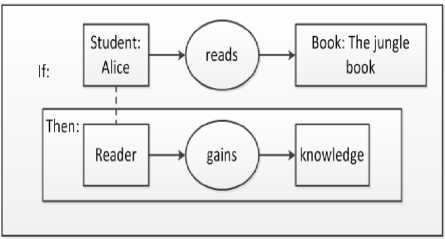
Fig.1. A Conceptual Graph (CG) Showing an If-Then Statement using Concepts and Relations.

Conceptual graphs can also use directed edges to show the total ordering of concepts and relationships. An incoming edge at a relation indicates first argument and the outgoing edge indicates the last argument for the relation. Conceptual graphs can be used for knowledge representation, reasoning and in most cases natural language processing [4]. A CG (simple conceptual graph) can be seen as an extension of BG, a CG has existential quantifier, conjunction and negation represented through the edges. A CG can use these to write every possible FOL formula with the given knowledge. Hence CGs can be used as a graph based KRR formalism or can be an intermediate graph based interface for other formalisms and natural language [12]. Projection operation, describing logical subsumption in conceptual graphs, can be used for logical reasoning in addition to the logical formulae. Hierarchical knowledge representation and integration is possible through layering [25].

In 2013, conceptual graphs were used in capturing the African traditional medicine and treatment knowledge [26]. African traditional medicine treatment would require knowledge from physical, social and spiritual domains as a disease in this system is considered to be a result of a problem or an imbalance in the three domains. The motivation of this work was to capture current knowledge and seek ways to enhance it with or without conventional and other medicine. Hence representing this knowledge along with strong reasoning is desired, making use and verification of Africa traditional medicine in mainstream healthcare. Properties are defined within the domain conforming to any one of the requirements specified in the set of guidelines in African traditional medicine system. Using nested conceptual graphs for representing hierarchically structured knowledge, a set of property specification patterns are defined as reference. Then using these patterns and properties any natural language specification of a property can be mapped to a specific requirement and vice versa.

In this application, reasoning was done using FOL logic extended with temporal contexts and temporal discursive terms. Conceptual Graph was used as visual representation with equivalent computational tree logic (CTL), with mapping of patterns from other formalisms such as CTL to CG. This enables obtaining structure of a pattern from CG to match the given requirement in the African traditional medicine methods. This serves as a very good example of implementing graph models in a contemporary, large and complex application in which significant knowledge representation and reasoning are required.

• IV.    Concept Graphs

Concept Graphs are multigraphs and bipartite graphs, similar to conceptual graphs [10]. Concepts and relationships are represented as nodes and edges respectively. Concept graphs can enable direct mapping of concepts and relationships in a relational data base; they offer semantic representation for processing natural language text into knowledge; they have strong support to FOL reasoning for bringing out implicit relationships and hence add to existing knowledge [11]. Syntactically and semantically concept graphs are very similar to conceptual graphs. An unification of conceptual and concept graphs has been proposed [10]. As multi-bipartite, concept graphs can represent affiliation relationships, as used in social network analysis.

Popular tool which can assist in creating concept graphs is cTakes 3.1.2 with YTEX [27] and other graph drawing software including the tools from graph databases such as Neo4j [28] can also be used. Ondex [29] software is available as programming API platforms.

In 2014, Agarwal et al [30] used conceptual graphs for similarity search, for retrieval of web documents with desired media content. The problem addressed in this case was to retrieve required web media while reading a given document in an e-reader. The system proposed uses concept graphs, a representation very close to conceptual graphs [31], for mapping the query objects. Then the actual query words are determined from the concepts and their relationships from concept graph. The motivation for this work was that in rich interactive applications relevant content based on user behavior has to be retrieved, without a separate session for the user to visit a search engine and enter the query keywords. Such a facility requires identification of currently relevant context(s), and then a strategy for retrieving relevant content without user intervention.

The first part of the challenge has to be solved using the content in the currently processed document, where concept graphs can be utilized. The context identification is not mere expansion of query terms using synonyms, but through the knowledge obtained from a concept graph. The model proposed was as follows. G = (U, E) is the universal concept graph over the set of all concept phrases (providing context). Concepts are represented by vertices (U), and relationship across any two concepts is defined as an edge in E. Related concepts can be reached from one another as long as relationship edges provide reachability. If s is a document, C(s) represents all the concept phrases which are in s. C(s) may be a subset or an equal set of U. Considering all core concepts relevant to s as T(s), where T(s) ⊆ U, and T(s) ⊄ C(s), union of T(s) and C(s) is Π (s), which represents of all concept phrases relevant to document s. A representation of s can be (C(s), T(s), Π (s)).

In an application such as an e-reader, when a document is read by the user, concept phrases can be identified retrieved from the document representation. If there are more than a specified n concept phrases, a simple ranking approach can help in choosing top n concept phrases. T(s) can be built/updated with picking top m core concept phrases from G. Search without user intervention through a search engine can be initiated, using duplicates across C(s) and T(s) only once, and resulting web media can be analyzed for related concepts (from file name, file type and other details related to the media). Concept phrases for the media can be generated (referring to existing concept graph of concept phrases for document s using C(s), T(s) and Π (s)) and can be chosen as a relevant web media for the current document read by the user at the ereader. A neighborhood criterion can be applied to limit matched concept phrases from document and web media. This overall approach is different from a traditional nonuser initiated search for relevant documents, by using much complex mechanism for finding relevancy and the possibility of further enhancement of representation of documents through generalization of concepts and their relationships using normal set operations. However a limitation of this approach is that with many results from search engine, building concept phrases and relating concept phrases for the document from the concept graph for each result, can be quite complex and costly.

• V.    Semantic Networks

  Semantic network is a knowledge representation scheme using concept of triples. Applied on web documents for knowledge representation, semantic network is a foundation for semantic web. The original semantic web idea was proposed by Tim Berners-Lee in 2001[32].

A semantic network is made up of concepts and their relationships, which are represented as triples. For example, F(x, y) can be considered as a semantic relationship, where F is a predicate logic formula, and relates objects x and y. X is a concept or entity in domain and Y is a concept or entity in a range. Interconnected concepts through such triples form a semantic network. Semantic networks are represented as graphs. Each concept or entity is a node. Nodes can be labeled for details. Arcs (edges) in a semantic network may be directed or undirected, and connect nodes. Arcs usually have specified relationship with which the connected nodes are related. If an arc e connect objects x and y, x is the subject and y is the object in predicate logic triple [5].

Figure 2 shows an example of a semantic network with nodes in a vehicles domain using ‘is a’, ‘has’, and ‘can transport’ relationships. The following are some assertions from the example:

Car is a Vehicle,

Bicycle is a Vehicle,

Truck has Wheels,

Truck can transport Bicycle

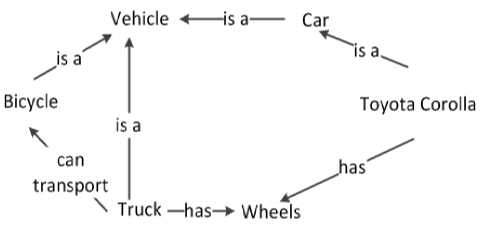
Fig.2. Example for a Semantic Network

Thus knowledge can be represented through a semantic network. Semantic web is a goal and a design for capturing the knowledge in web documents (initially from within defined domains, later to encompass knowledge in entire web), for machine processing to take decisions. Semantic network usually makes use of Description Logic (DL), a subset of FOL for logical reasoning [5] on RDF and RDFS.

Abello et al [33] studied semantic web approach for exploratory OLAP (OnLine Analytical Processing). OLAP is usually used in Data Warehouses and Data Mining fields where usually condensed, subject oriented, time dependent and data for business decision making are involved. Most of the data analytics and data mining currently can be strengthened with adding knowledge from World Wide Web, instead of depending only on condensed data from internal business transactions. But the knowledge available in the web is usually not in suitable format for knowledge acquisition or reasoning directly. Hence Semantic Web can be used to first gather the relevant knowledge from web, represent in a suitable form for the OLAP system, and reason out implicit knowledge from acquired data. The power of semantic web to use precise semantics from data can be very useful to build inferences while reasoning. Such semantic web integrated OLAP is known as exploratory OLAP.

There are several tools available for semantic networks and semantic web. One of the most famous tools is Protégé[13]. It is an open source, freeware knowledge representation and ontology editor framework. The reasoners in Protégé, such as HermiT [14] and FaCT++ [15], are incorporated as plugins. Standards such as RDF/RDFS and OWL, built over XML, can be used for KRR in semantic web. Javascript Object Notation (JSON) is another popular human readable notation for representing RDF triples [34]. Semantic networks and semantic web, though widely used currently, will have to undergo better unification of components and less complex implementations to truly take over KRR across the web [34].

• VI.    Inference Graphs

Inference graphs were proposed and developed by Schlegel and Shapiro [7][35][36] for KRR from propositional graphs. Inference graph is a reasoning graph and is capable of backward, forward and bidirectional reasoning. It can support concurrent processing for reasoning using propositional logic.

The biggest advantage of concurrency in reasoning is that data and knowledge can be used to solve a problem s with different approaches at the same time, provided that the problem can be approached in multiple approaches.

Inference graphs are made up of nodes and arcs (edges). Every rule is represented as a rule node in the graph. A rule node is capable of inference operations, using a set of rules known as Rule Use Information (RUI) set. The rules in an RUI explain (a) which antecedents of a rule are false or true and (b) how (a) was deduced from available information. There can be nodes representing functional terms or non-atomic formulae, labeled as wfti, where i is some integer. Each formula can be marked as an ‘and’ or ‘or’ entailment, meaning that the result of true or false computed from this node is dependent on all or any input being true.

Arcs in inference graphs can be either antecedent or consequent arcs, representing direction of message flow. Provisions are there in representation to immediately process the messages or put them on a queue at every node [37].

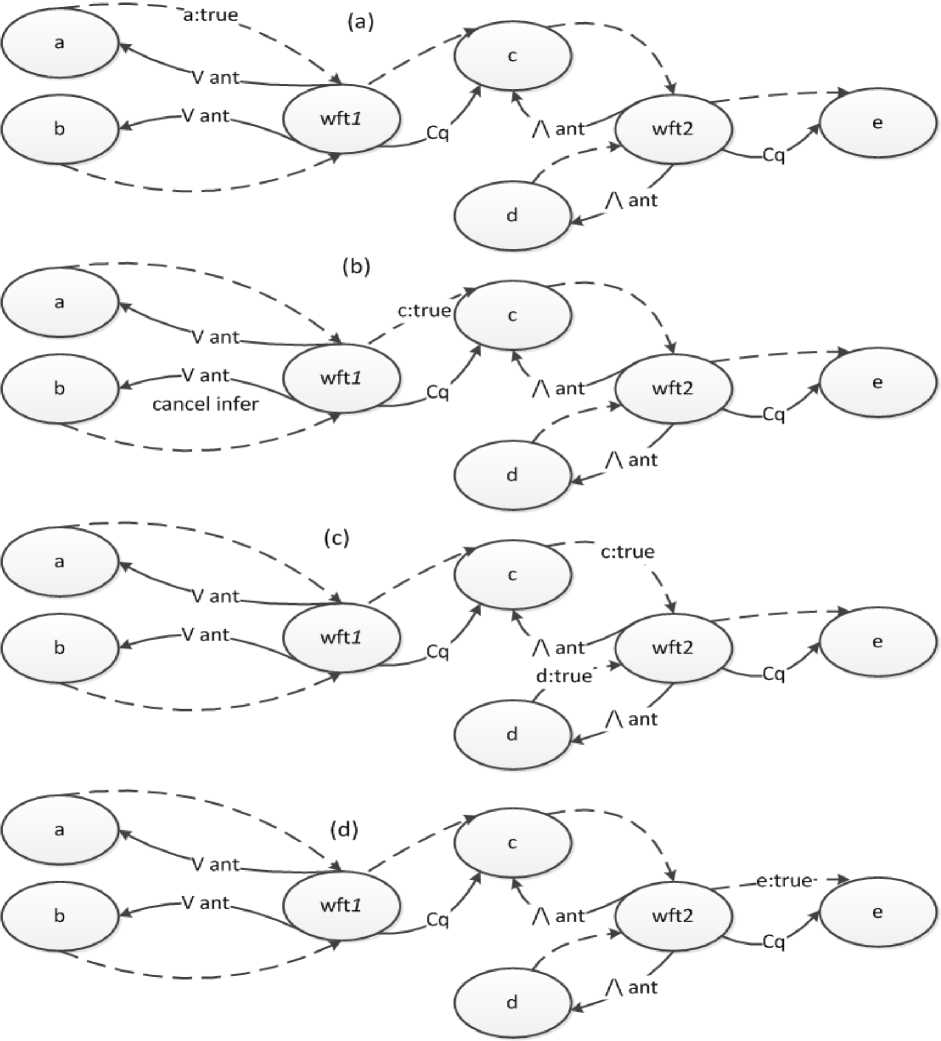
Fig.3. Inference Graph Example with Entailment, Antecedents and Consequents (Adapted and Modified From [35])

Consider the example given in figure 7 (adapted from [35]). There are two non-atomic formulae wft1, and wft2. The first non-atomic formula wft1 has an or entailment over its inputs a and b, and there is a consequent node c. The second non-atomic formula wft2 has an and entailment over its inputs c and d, and there is a consequent node e. Every node is connected to another node by two arcs, explaining the relationships. For example, a is connected to wft1 as an antecedent node and the dotted arc represents the truth value computed from a. Node c is connected from wft1 as a consequent node. The node wft1 has an or entailment over nodes a and b. The dotted arc from wft1 to c, can pass the nonatomic formula result computed at wft1. The node wft2 has c and d as antecedents and has an and entailment over them.

In Figure 3 (a), the node sends a message with value true to wft1. Wft1 can inform other nodes in the or entailment that no more inference is needed through a ‘cancel infer’ message. Now the result from wft1 is passed to node c, the consequent node in (b), the directed arc with Cq label highlighting this relationship. Node c passes the message to node wft2 in (c). If we assume that node d also sends a computed true to wft2 (c), then since the and entailment is satisfied, the node wft2 can send a ‘true’ message to node e (d).

This example shows representation in inference graphs, node and arc types, and how the computation results are passed from a node to another. Tools such as SNePS and CSNePS are available to create and use inference graphs, including programmatic API support. Logic support is available for First Order Predicate Logic (FOPL) and an extension of FOPL known as LA, which can handle indefinite terms defined arbitrarily. One of the main advantages of inference graphs is that concurrent processing is available.

With most of knowledge based systems running on parallel hardware, it is imperative that better performance can be elicited by using inference graphs in knowledge acquirement and building scenarios, as appropriately [37].

• VII.    Causal Bayesian Networks

Causal Bayesian Networks (CBN) is based on Bayesian Networks. Bayesian Networks (BN) have been researched and used in probabilistic reasoning for several decades [8]. BN depends on probability, probability distribution and the Bayes theorem (Given two events X and Y such that P(X) ≠ 0 and P(Y) ≠ 0, then,

Р (X | У) = ^Р(У ^^Р(х) (1)

Bayes theorem is used when conditional probability of P(X|Y) is not known but should be computed, and the conditional probabilities of P(Y|X), P(X) and P(Y) are all available. Such Bayesian inference is extremely useful when all elementary events in a sample space, their respective random variables and values for joint probability distributions are not available. Bayes inference allows us to compute probabilistic relationships among identified random variables [8].

In a directed acyclic graph G with ascendant descendent relationships among nodes, if a joint probability distribution P of random variables V can be defined with each X Є V, {X} conditionally independent of its descendants (given all parents), then G and P satisfy Markov condition. (G, P) is a Bayesian Network if (G, P) satisfies Markov condition. Several large scale systems in various domains have been successfully built using Bayesian Networks [8] and Bayesian Networks still offers a fertile research area. Causal Bayesian Networks (CBN) is similar to BNs but with a difference in association between any two nodes. In a BN, if for any two vertices X and Y, if there is a directed edge from X to Y, only if Y is a directly caused by X, then the resulting BN is a CBN. That is the significant difference is all the edges in CBN explicitly and show direct causal relationships only, between any two nodes in the DAG [8].

Yu et al [38] used CBN recently for bridging causal relevance and mining emerging patterns from high volume and high dimensional data. In data mining, association rule mining is usually used extract patterns based on support and confidence information (usually as probability values). Such identified patterns will be used for predictions later in the same domain using rules. However, with extremely large datasets (as in Big Data scenarios) with high dimensional data, prohibitive numbers of rules can be elicited. Such high numbers of rules result in highly complex processing and overall degradation of the system. This issue can be addressed by building CBNs with causal relevance and using it for emerging patterns identification. This approach reduced the pattern space significantly and resulted in faster and better emerging patters identification and prediction.

Several excellent tools and API programmatic support kits are available for BN and CBN, such as OpenMarkov [39], Graphical Models Toolkit [40], openBUGS [41], Bayes Series [42], and Netica [43]. Direct causal relationships help in having faster processing in all aspects of KRR with only direct dependencies included in the graph. Probabilistic reasoning and causal relevance available in CBNs have proven to be very useful in KRR while dealing with ambiguous and uncertain scenarios.

• VIII.    Observations

A comparison overview of the surveyed graph models is given in Table 1. Conceptual and Concept Graphs, since multi-bipartite, can naturally represent and support operations for affiliation in social networking analysis. Their abilities to nest, hierarchical, conditional and temporal representations can assist in data intensive scenarios. Semantic network’s deductive power with predicate logic and ontological expressivity can be helpful in analyzing data with context and reasoning. Excellent tool and API support, and wide use in industrial applications make semantic network a strong contender for graph based KRR in contemporary systems. Inference graphs, since designed with concurrent reasoning in mind, can be very helpful in realizing efficient processing of voluminous data, if concurrency can be employed in the scenario. Similar to BNs, CBNs offer inherent causal relationship construction and identification and probability distribution over a large knowledge base.

Probabilistic reasoning can be extremely effective over other reasoning approaches in uncertain and ambiguous scenarios.

Using graph models for KRR in Big Data is not free from challenges. For all the models there are some common limitations such as for large knowledge base the graphs becoming too large to perform operations within expected time. Changes in existing knowledge can increase the overhead cost of maintaining the graph’s nodes and edges.

Resolving conflicts from contradictory knowledge can be quite challenging as well. However, some of these challenges can be addressed by sophisticated tools. Most of the tools listed above are still evolving to address these issues. A practitioner may use the observations in the table for selecting a graph model for KRR for building an application. Table 1 below compares Conceptual Graph, Concept Graph, Semantic Network, Inference Graph and Causal Bayesian Networks on the factors graph type, network/graph representational capabilities, reasoning and usage capabilities.

Table 1. Comparison Overview of Popular Graph Models for Knowledge Representation and Reasoning

Graph Models Criterion	Conceptual Graph	Concept Graph	Semantic Network	Inference Graph	Causal Bayesian Network
Graph type	Multi, bipartite graphs with no odd length cycles	Multi, bipartite graphs with no odd length cycles	Directed or undirected graph	Multi, directed, channel capable graphs	Directed acyclic graph
Network / Graph Representational capabilities/ criteria
Node type/ capabilities/ representation	Concepts and relationships	Concepts and relationships	Subjects and objects (used in triples)	Rule and based on arc direction can be considered antecedent or consequent	Random variable in a domain
Node attributes	Type and individual marker	Type and individual marker	Labeled and marked	Represents rule, proposition/ function symbols and nonatomic formulae	Each node is associated with a conditional probability table showing dependencies
Edge type /capabilities /representation	Association of concepts and relationships	Association of concepts and relationships	From – to association (per triple)	Showing antecedent and consequent relationships through direction	Show direct causal relationships between any two nodes in the CBN
Edge attributes	Multiple, may be directed to show sequence, total ordering through numeric labels	Multiple, may be directed to show sequence, total ordering through numeric labels	Directed or undirected, single, without ordering	Directed, capable of getting associated with channels for carrying messages, without ordering	Directed, and single between any two nodes, with no specific ordering
Reasoning capabilities/ criteria
Logic	FOL, Predicate, can be extended to higher order	FOL, Predicate, can be extended to higher order	FOL Predicate Logic, DL, DL-Lite	Forward/backward reasoning with concurrency support	Probabilistic reasoning with causal relationships
Causal resolution	Yes, indirectly	Yes, indirectly	Yes, indirectly	Yes, forward, backward and bidirectional	Yes
Implicit knowledge inference	Yes, through graph operations	Yes, through graph operations	Yes	Yes	Yes
Usage Criteria
Domains/applications where used recently	Medicine, software engineering with high volume and complex reasoning relationships	Semantic Similarity, social network analysis	Ontological applications, Exploratory OLAP and data mining	Reasoning system, logic based cognitive systems, and voluminous KRR	Data mining, emerging pattern identification and prediction in high volume, high dimensional data
Tool support	CharGer, CG Mars Lander, CoGITaNT, CPE, GoGui and Prolog+CG	cTakes 3.1.2 with YTEX, tools from graph databases such as neo4j	Protégé, WordNet, SNePS, MultiNet	SNePS, CSNePS	openBUGS, OpenMarkov, Graphical Models Toolkit, Netica
API support	Amine, Cogitant, Notio	Ondex	RDF/RDFS Toolkits, Jena with OWL, SPARQL	SNePS, CSNePS	OpenMarkov, Graphical Models Toolkit, Bayes series
Standard/Open representational schema / notation	Conceptual Graph Interchange Format (CGIF)	Conceptual Graph Interchange Format (CGIF)	XML/RDF /OWL	CSNePS based representation, nonstandard	No standard representation. Application specific schema.

• IX.    Conclusion

Contemporary and emerging systems in all domains depend on knowledge based systems for acquiring, preparing, using and extending known knowledge with implicit reasoning. This survey has covered the significance of KRR in recent trends and surveyed graph models such as Conceptual Graphs, Concept Graphs, Semantic Networks, Inference Graphs and Causal Bayesian Networks.

Observations have been made on KRR capabilities and applicability in real world data intensive scenarios of these models. This survey has provided a review of popular graph models for knowledge representation and reasoning.

In this study a comparison of popular graphs for knowledge representation and reasoning is done considering factors such as of Network / Graph Representational capabilities/ criteria, reasoning capabilities/ criteria and Usage Criteria. Such a comparison can assist as a reference when a practitioner has to choose a specific graph model for use in an application dealing with knowledge representation.

Graph models for KRR, though have been under active research for several decades, still is a fertile research area. Rich focus avenues are possible including building reasoning abilities for disconnected scenarios in large graph representation, fitting within real world applications in Big Data area to compare performances and finding effective methods for cross verification of crucial and fundamental knowledge stored in large graph models, with human domain experts.

Acknowledgement

The authors wish to thank the anonymous reviewers for their valuable comments.