Гравитационная модель оценки вовлеченности стран в мировую торговлю

В современном быстро развивающемся мире, важное значение имеет торговля, а именно внешняя торговля. Благодаря внешним связям стран преодолеваются многие проблемы, такие как ограниченность ресурсов и узость внутреннего регионального и национального рынка, создается возможность организации массового, крупного производства, возрастает эффективность внедрения новой техники и технологий, увеличиваются накопления, темпы экономического роста и более рационально используются ресурсы стран.

Для того чтобы исследовать и проанализировать эффективность экспорта и импорта между той или иной страной, регионом, группировкой экономисты вывели различные модели международной торговли, одной из которых является гравитационная модель.

В экономической науке выделяют несколько вариантов гравитационной модели и каждый исследователь, который так или иначе собирается проанализировать экспорт и импорт выбирает подходящую ему модель. При разработке различных видов гравитационных моделей используются показатели численности населения, площади стран, протяженности границы, а также фиктивные переменные, отвечающие за социально-политические, климатические и другие различия.

Регрессионный анализ даёт возможность оценить влияние этих факторов, на основе данных о фактических размерах товарооборота между странами и регионами. Полученные результаты - это параметры гравитационной модели, которым присущ характер эластичности. Соответственно, они показывают, на сколько процентов может возрасти товарооборот между странами, если соответствующий фактор повысится на 1%. Как правило, данная модель выводится либо в степенной, либо в линейнологарифмической форме[1].

В научной литературе для моделирования внешней торговли чаще всего применяются модели, основанные на одной из главных теорий международной торговли.

• >    Модели, основанные на предположениях Армингтона [2]. В основу положена теория того, что каждая страна производит только один товар, и потребители выбирают и проводят различия между товарами, произведенными в разных странах;

• •    Модель выдающегося классика политической экономии Давида Рикардо [3]. Его модель основывается на теории сравнительных преимуществ. Он считал, что каждая страна увеличивает производство количества единиц сравнительно дешевого товара за счет единиц сравнительно дорогого. Получается, что выигрыш от торговли и ее масштаб пропорциональны масштабу сравнительного преимущества.

• •    Новая теория торговли Кругмана [4].

Кругман выделял внутриотраслевую торговлю, как осуществление торговли между одинаковыми странами.

Все вышеперечисленные теории могут применяться для моделирования величины торговых потоков. Но для такого моделирования необходима информация о спросе и предложении товаров на рынке каждой из рассматриваемых стран, при учтение внутреннего и внешнего предложения. Существует много нюансов, так как помимо того, что требуются знания о конкуренции на рынке, о предпочтениях потребителей, устройстве рынка, характере конкуренции, взаимозаменяемости местных и импортных товаров, необходимым является знание конечных цен на отечественную и импортную продукцию или хотя бы разницы этих цен на рынке экспортера и импортера.

Достаточно распространенным подходом к моделированию в таких условиях является аппроксимация (замена одних объектов другими) издержек международной торговли расстоянием между торгующими между собой странами.

При этом достаточно очевидно, что расстояние между торговыми партнерами является не самым надежным инструментом для моделирования торговых издержек: на формирование конечной цены на рынке сбыта могут влиять особенности прохождения таможни, вид груза, определяющий выбор вида транспорта, тарифная политика транспортных компаний, особенности местной инфраструктуры и т.д. Не смотря на это, именно показатель удаленности и близости между торгующими странами используется наиболее часто благодаря относительной простоте сбора этих статистических данных в гравитационной модели.

Теория А. Айзарда на основе закона всемирного тяготения И.Ньютона.

Одним из первых научных деятелей, обосновавших теоретические аспекты гравитационной модели был А. Айзард. Начало было положено в 20 веке, когда был бум количественных методов в экономической географии.

Исходной точкой для появления таких моделей послужила аналогия с Законом всемирного тяготения Ньютона, который гласит, что сила гравитационного притяжения F между двумя физическими телами прямо пропорциональна массам этих тел, m 1 и m2, и обратно пропорциональна квадрату расстояния d между ними:

где G - гравитационная константа.

Айзард попытался применить аналог этой формулы к описанию потоков товаров и услуг между странами и/или регионами.

Самым главным звеном этой модели является внешнеторговый оборот, который находится в прямой зависимости от экономического потенциала торгующих стран и в обратной от расстояния между ними. Ведь именно размер экономики определяет спрос и предложение, а расстояние между партнерами важно с точки зрения издержек на торговлю товарами, которые растут с увеличением расстояния между странами.

Гравитационная модель Тинбергена.

В истории гравитационной модели, одна из первых работ в которой она была использована, является статья голландского экономиста Яна Тинбергена 1962 года [5]. Модель связывает объем экспорта из одной страны в другую со следующими объясняющими переменными: ВВП экспортирующей страны, ВВП импортирующей страны и географическое расстояние между двумя странами. Модель является достаточно простой, как отмечал сам Автор.

Тинберген добавлял фиктивные переменные, имеющие значения «0» или «1» на участие стран-партнеров в различных торговых соглашениях.

Таким образом, мультипликативная формула, связывающая все вышеперечисленные переменные принимает следующий вид:

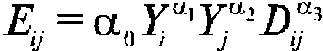
Расшифровка символов:

-I- E ij — экспорт из страны i в страну j,

J- Y_i — ВВП страны i ,

J- Y j — ВВП страны j ,

J- D_i j — расстояние между странами i и j ,

J- α i — оцениваемые коэффициенты эластичности объема экспорта по соответствующим переменным.

Данная модель имела теоретический и эмпирический успех и подверглась дальнейшему широкому использованию в международной торговле. Но работа Тинбергена не имела конкретного теоретического обоснования данной спецификации торгового уравнения. Можно выделить еще несколько работ, в которых также не наблюдалось полного теоретического обоснования: [Poyhonen, 1963a, 1963b], [Pulliainen, 1963], [Geraci, Prewo, 1977], [Prewo, 1978], [Abrams, 1980] и другие.

В последующие годы разные ученые экономисты - географы старались разработать теоретическую основу модели, это был поиск с заранее известным результатом, который хотели эконометрически обосновать. В числе таких работ можно отметить статьи: [Leamer, Stern, 1970] с вероятностной моделью; [Leamer, 1974], в которой параллельно использовались переменные из гравитационного уравнения и теории Хекшера—Олина; [Anderson, 1979], опиравшуюся на микрообоснования и гипотезу Армингтона; [Bergstrand, 1990], в которой автор моделировал монополистическую конкуренцию, и др.

Парадокс границы Маккалума.

Виднейший ученый 20 века Маккалум в 1995 году также разработал гравитационную модель, в которой был получен эмпирический результат, ставший известным как «парадокс границы» ( border puzzle ).

В этой работе представлялось следующее соотношение:

but = a, + ajny + a. Ini' + a,ln^/ + a ,    (3)

J;          I                      г            л                      4 и           - У

Основные обозначения:

• x ij — экспорт из региона i в регион j

• y — ВВП регионов

• d ij — расстояние между регионами

• δ — фиктивная переменная, равная единице, если регионы находятся в одной стране

  Уравнение (3) было протестировано и проанализировано на данных 1988 года по торговле10 канадских провинций и 30 штатов США. В то время на них приходилось около 80% общего объема американо-канадской торговли.

Непонятным и парадоксальным для исследователей являлось то, что взаимная торговля между канадскими провинциями оказалась в 22 раза больше, чем торговля провинций со штатами США. Объяснением этому могло являться то, что граница между США и Канадой уже была настолько стерта, что снижала быстрыми темпами взаимную торговлю. Несколько лет ученые не могли найти этому рациональных обоснований.

Результат, полученный в статье Маккалума [6], породил целую серию исследований, посвященных «парадоксу границы».

В 2003 году ученые смогли добраться до истины и была предложена полноценная теоретическая модель, предсказывающая «парадокс границы», в работе [Anderson, Wincoop, 2003]. Теория позволяла получать состоятельные и эффективные оценки в эмпирических исследованиях[9].

После максимизации функции полезности потребителя авторы получают следующий вид гравитационного уравнения:

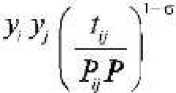
_ 0j

" yW

где xij — стоимостной объем экспорта из региона i в j; yi = Sxij — суммарный доход региона i; yW= Sj yj — номинальный доход мировой экономики; Oj—yj /yW; о — эластичность замещения между товарами; tij — издержки транспортировки из i в j; Pv „=£ Pv «ПР /^j — рекурсивное соотношение для введенного в процессе преобразований ценового индекса.

Основные обозначения схожи с другими гравитационными моделями, но имеют дополнительные переменные, такие как номинальный доход мировой экономики, эластичность замещения между товарами т.д., которые и являются уточняющими, позволяющими с теоретической точностью определить зависимость экспорта и импорта от местоположения торговых точек.

Уравнение (4) подразумевает то, что объемы торговли между какой-либо парой стран при прочих равных будут больше, чем между другой парой стран, обладающих меньшим ВВП и наоборот.

Повтор расчетов [McCallum, 1995] с включением в модель «многостороннего сопротивления» показал, что наличие границы снижает объемы торговли всего на 20—50%, то есть многостороннее сопротивление объяснило большую часть «парадокса границы»[7].

Гравитационная модель Андерсона в дальнейшем стала классической моделью и широко использовалась в научных исследованиях[8].

Так как в данной работе рассматривается вовлеченность России в международную торговлю посредством гравитационной модели, следует уточнить, на что именно влияет вышеуказанный показатель и насколько сильно это воздействие.

Среди важнейших показателей вовлеченности в мировые торговые процессы, как уже указывалось выше, объемы импорта, экспорта, ВВП страны, объемы потоков ПИИ, участие в международных экономических организациях (ВТО, МВФ, МБРР и т. д.), количество ТНК на территории страны, объемы капиталов резидентов за границей и объемы транзакций по покупке или продаже услуг и товаров.

Тинберген первым применил эту гравитационную модель для анализа международной торговли в 1962 году и многие другие последовали за созданием серии эконометрических моделей двусторонних торговых потоков. Как говорится выше формула гравитационной модели Тинбергена показывает связь между стоимостным объемом экспорта из страны i в страну j (xij), экономическими размерами экспортера и импортера (yi и yj) и издержками торговли между странами (tij), где α > 0, β > 0, γ> 0. x ij = k* (y i ^a* y^b j )/t^y j ¹ .

Ряд исследований во многом способствовали созданию теоретической основы гравитационной модели, показывающей, что уравнение гравитации может быть получено из ряда различных международных торговых операций.2

При использовании гравитационной модели с простой формулой, не учитывающей географические особенности стран, главными показателями являются ВВП страны экспортера, ВВП страны импортера и издержки торговли между странами. К последним относятся такие показатели, как таможенные тарифы; транспортные издержки; членство в валютных и торговых союзах, волатильность обменного курса; политические союзы, военные блоки; языковые барьеры, колониальные связи, общая религия; информационные барьеры; контрактные издержки, географические особенности расположения страны.

Однако если сравнить общий подход и гравитационную модель, общими среди них все же будут являться макроэкономические показатели стран и свобода доступа на внутренний рынок. Парадоксально, но влияет вовлеченность страны в международную торговлю на те самые показатели, которые ее определяют. Чем выше индекс вовлеченности страны в международную торговлю, тем выше, соответственно, показатели, ее составляющие.

Именно в повышении объемов торговли и выражается интегрированность стран в мировой рынок. Чем выше индекс, тем скорее вырастут отдельные макроэкономические показатели страны, связанные с внешнеторговой средой государства.

Интегрированность страны в международную торговлю оказывает непомерное влияние на имидж страны в глазах зарубежных государств и частных торговых партнёров, существующих и потенциальных. Значимость международного признания сложно переоценить, однако зачастую это признание в качестве партнера оказывается временным и спекулятивным, зачастую служит политическим целям. Чем более интегрирована страна в мировые хозяйственные процессы и чем ниже барьеры для входа на ее рынок, тем более высок вышеуказанный показатель, при этом довольно часто это становится проблемой, так как от него напрямую зависит деловой климат страны, а также фактическое благосостояние народа. Возьмем, к примеру, экономический кризис в РФ в конце 90-ых годов на постсоветском пространстве. Россия, которая в то время рвалась стать частью мирового сообщества, в том числе с экономической точки зрения, открыла рынок ценных бумаг для свободного входа всевозможных игроков на рынке ценных бумаг, которые до 1997-го года охотно вкладывались в предприятия и государственные ценные бумаги, а в периоды внутренней нестабильности или при первых «тревожных звонках» из уст экспертов (зачастую самих спекулянтов, таких как Джордж Сорос), капиталы выводили, и искали «горячих денег» в других точках мира, обрушая при этом всю и без того нестабильную финансовую систему РФ. В данном случае вовлеченность РФ в мировые торговые процессы сыграла на руку игрокам рынка и оказалась губительной для экономики целого государства, как и в случае с Аргентинским и Азиатским кризисами в тот же период.

Также негативным образом данный показатель отразился на российской экономике после присоединения в марте 2014-го года Крыма, в результате чего против РФ были введены политические и экономические санкции в виде частичного запрета на некоторые товарные группы и запрете или блокировке многочисленных крупных экономических совместных проектов. Это, а также, как говорилось выше, девальвация рубля привели к резкому ухудшению делового климата и инвестиционной привлекательности Российской Федерации.

В качестве санкций мировым сообществом также были снижены сырьевые цены, повлекшие отток капитала, от чего больше всего пострадали страны с переходной экономикой, чей ВВП, по данным доклада ВТО 2016 года3, в 2015 снизился. В Российской Федерации и на Украине проблемы с платежным балансом усугубились политическими конфликтами. Резкое падение курса национальной валюты и высокая инфляция сбили внутренний спрос и углубили экономический спад. Это в свою очередь сказалось на соседних странах, для которых Российская Федерация служит крупным рынкоми источником односторонних переводов.

Однако не всегда примеры бывают негативными. Вовлеченность страны в международные торговые процессы также может ей помочь выбраться из депрессии и послужить толчком к росту в случае принятия правильной внешнеторговой политики – протекционистской, либеральной или же смешанной, что и сделала РФ.

По итогам 2017 года Россия входит в число ключевых участников международной торговли, занимая 17 место по экспорту товаров, и обладая большим внутренним рынком. На данный момент участие России в международной торговой системе характеризуется такими показателями как динамика экспорта и импорта, товарная структура внешней торговли, доля России в импорте торговых партнеров.

Кроме того, вовлеченность почти всех стран в региональные торговые соглашения, которые охватывают более половины мировой торговли, дает им новую возможность сотрудничества без прямого подписания каких-либо договоров о преференциальной двухсторонней торговле, что заметно упрощает вход на рынок иностранных государств. Например, в ВТО входит 164 страны, по данным 2016 года, в ЮНКТАД – 194, что составляет 70 до 90% всех стран мира.

Для оценки гравитационной модели мы обращались к данным ВТО, Русстата и некоторым периодическим изданиям.

Зависимая переменная в гравитационной модели двусторонней торговли (сумма экспорта и импорта) между парами стран, а продукт ВВП и продукт ВВП на душу населения используется в качестве независимых переменных[10,11].

Таким образом, получили следующее уравнение гравитации торговли для нашего анализа:

• •   Log(Trade ij ) = β 0 + β 1 log (GDP i * GDP j ) + β 2 log( PCGDP i * PCGDP j ) -

• β3log(Distanceij) + β4(Complang_off) + β5(Colony) +ξij,     (1)

• •    где Trade ij = стоимость общей торговли между страной i и страной j;

• •    GDP_i (GDP j ) = валовой внутренний продукт страны i (j);

• •    PCGDP i (PCGDP j ) = ВВП на душу населения в стране i (j);

• •    Distance ij = Расстояние между страной i и страной j[15];

• •    Comlang_off = общий официальный язык (фиктивная переменная);

• •    ξ ij = - это период ошибки регрессии.

Согласно экономической теории модели, ожидаем положительные значения β1, β2, β4 и β5 и отрицательного знака для β3.

Данные для анализа торговли между Россией и Китаем приведены в таблице4.

страны	показатели	Россия	Китай
Trade		84008000000
GDP		1.461.000.000.	11.508.000.000
PCGDP		10.130	8.315
Distance тыс. км.		Наличие общей границы
Comlang_off		Отсутствует

Таблица 1.

Расчет по практической формуле Тинбергена (1) для России и Китая привел к следующему результату:

β 0 =1

Log (84008000000) =  1+ log (1.461.000.000.*11.508.000.000.) + log

(10.130*8.315.) + 0.76 25,2 =64,36

Logtrade =39,16

Показатель оказался выше ожидаемого, так как в формуле учтен факт наличия общей границы, отрицательным фактором является отсутствие общего официального языка между торговыми партнерами. В данной формуле не учтены факторы наличия санкций и участия в одних международных экономических организациях.

Такой высокий показатель обосновывается положительным взаимодействием этих двух стран в торговле за последние несколько лет.

Ниже представлен график, отображающий рост торгового взаимодействия между Россией и Китаем по данным исследований EY [16].

2014        2015        2016        2017

6.8%        7.5%        8.3%        9.8%

Для торговых отношений между Китаем и Россией 2016 год ознаменовался 15-летием Договора о добрососедстве, дружбе и сотрудничестве. Это также означало, что прошло 20 лет с момента установления стратегического сотрудничества и партнерских отношений между двумя государствами. Ряд политиков заявили, что российско-китайские связи достигли нового исторического пика, что стало плацдармом для дальнейшего развития в 2017 году.

Помимо растущего сотрудничества в таких секторах, как электронная торговля, горнодобывающая промышленность, сельское хозяйство, развлечения и строительство, обе страны продолжали укреплять свои связи за счет увеличения торговых потоков. Масштабы сотрудничества росли в таких стратегических секторах, как нефть и газ, инфраструктура, оборона, авиация и даже ядерная энергия.

В январе 2017 года Россия стала крупнейшим экспортером нефти в Китай, превысив Саудовскую Аравию, а также торговые потоки между Китаем и Россией увеличились на 34% в годовом сопоставлении.

Согласно обзору EY Перспективы из Китая: как опасения относительно российского рынка влияют на китайские инвестиционные стратегии , российский рынок остается «очень привлекательным» на 28% и «привлекателен» для 45% среди 142 опрошенных инвесторов.

№ 1 российской нефти и инвестором № 4 по ПИИ в России. В то же время Китай является чрезвычайно диверсифицированным рынком, вторым по величине экономикой в мире, все более доминирующим в списке GF500 и фокусирующимся в прошлом году на исходящих инвестициях больше, чем когда-либо.

Статистика и нынешний уровень сотрудничества подтверждают быстро растущий интерес китайского бизнеса в России. И, что немаловажно, этот интерес уже связан с такими долгосрочными проектами, как «Ямал СПГ», «Свободный порт Владивосток» и высокоскоростная железная дорога, соединяющая Москву и Пекин.

Таким образом, действительно существует большой взаимный инвестиционный интерес между Китаем и Россией, и он продолжает расти. И для поддержания этого интереса на уровне отдельного китайского проекта в России важно не только вносить вклад от местных партнеров и правительства, но и от самих инвесторов [12].

Данные для исследования торговли между Россией и Нидерландами по гравитационной модели, представлены в таблице5[12].

страны показатели	Россия	Нидерланды
Trade	45 092 000 000
GDP	1.461.000.000.	771.000.000.000.
PCGDP	10.130	52.111
Distance тыс. км.	52.111
Comlang_off	Отсутствует

Таблица 2.

Log (45 092 000 000) = 1+ log (1.461.000.000. * 771.000.000.000.) + log (10.130*52.111) – log (5.557)+ 0.76 24.5=1+48,5 + 11,04 – 8,6 + 0,76

Logtrade= 28,2

Показатель оказался довольно ожидаем, так как в формуле учтен факт отсутствия общей границы, отрицательным фактором также является отсутствие общего официального языка между торговыми партнерами, отрицательно влияет достаточно низкий объём экспорта между странами.

Результат довольно положителен, и этому предшествуют потоки импорта и экспорта между странами а также то, что Россия и Нидерланды традиционно являются важными экономическими партнерами. Нидерланды являются третьим в мире и первым в Европе торговым партнером России и вторым иностранным прямым инвестором. В 2017 году российско-голландский товарооборот составил 39 504 485 368 долларов США, что на 22,40% (7 228 805 112 долларов США) с 2016 года (по статистике

Федеральной таможенной службы России). Нидерланды остаются российским экспортным пунктом (35 611 335 228 долларов США, что на 21,73% (6 356 711 346 долл. США) с 2016 года.) и номером 14-импортным партнером (3 893 150 140 долларов США, что на 28,87% (872 093 766 долларов) с 2016 года.). В 2017 году российско-нидерландский товарооборот составил 6,7769% от объема внешней торговли России [13].

Нидерланды экспортируют в Россию в основном сельскохозяйственную продукцию, продукты питания, химическую промышленность, машины и транспортные средства. Россия экспортирует в Нидерланды минеральные ресурсы и топливо, металлы и металлопродукцию.

К концу второго квартала 2017 года прямые инвестиции Нидерландов в Россию составили 67,8 млрд долларов (по данным ЦБ РФ), что составляет 11% от общего объема прямых иностранных инвестиций, накопленных в российской экономике.

В настоящем исследовании представлены результаты теоретического изучения гравитационной модели, а также практического, с помощью расчетов проведенных между Россией и странами Китая и Нидерландов. Рассмотрены основные подходы к созданию и применению гравитационных моделей торговли, предложена спецификация и методология оценки расширенной гравитационной модели, которая учитывает пространственные эффекты.

Важно заметить, что достаточно большое количество учёных-экономистов подходило к решению вопроса гравитации, что делает эту модель важной в современных экономических отношениях. Но большие проблемы доставляло найти не только эмпирическое, но и теоретическое обоснование модели, ближе всего к решению этой проблемы приблизились в своих работах Андерсен и Тинберген. Так, с помощью исследований «парадокса границы» Маккалума, Андерсон в качестве дополнительной переменной в гравитационное уравнение ввёл уровень ВВП на душу населения. Не мало важными при построение гравитационной модели оказываются такие необычные переменны, как: наличие общего языка, общей валюты, а также расстояния между странами или регионами.

При расчетах гравитационной модели между Россией и Китаем положительное влияние оказал большой объём торговли между странами, причем экспорт России в Китай оказался всего на несколько позиций ниже, нежели экспорт Китая в Россию. Наличие общей границы также имеет положительную направленность.

Что касается торговли между Россией и Нидерландами, тут ситуация немного хуже, ведь нет общей границы, а гравитационная модель предполагает, что чем ближе субъекты тем положительней торговля. Но торговля между странами за последние годы набирает всё больший оборот в разных отраслях промышленности и сельского хозяйства, что также даёт о себе знать в результатах расчетов.

По результатам исследования можно сделать ещё несколько важных выводов:

• 1.    Построенная пространственная гравитационная модель внешней торговли может быть использована для описания объемов и маршрутов внешнеторговых товарных потоков России и других стран и для прогноза их реакции на изменение ряда факторов. Значения коэффициентов модели, полученные при эконометрическом оценивании, не противоречат сформулированным теоретическим гипотезам.

• 2.    Расстояние между импортером и экспортером, которое является проксипеременной для торговых барьеров, оказывает значимое отрицательное влияние на объемы торговли; при этом следует принимать в расчет не расстояние само по себе, а величину расстояния в сравнении с расстояниями до других торговых партнеров. Данный результат полностью соответствует выводам, полученным в международных исследованиях по рассматриваемой тематике.