Гравитационно-скалярная неустойчивость космологической модели на основе двухкомпонентной статистической системы с асимметричным скалярным хиггсовым взаимодействием фермионов

В последние годы в связи с одновременным прямым экспериментальным обнаружением в 2016 г. гравитационных воли и Черных Дыр [1], [2] и последующим их исследованием были подтверждены, в частности, более ранние косвенные наблюдения по орбитам звезд сверхмассивпой

Черной Дыры в центре нашей Галактики с массой порядка 4 • 106М0(см., например, [3], [4]), а также существование сверхмассивиых Черных Дыр в центрах галактик и квазаров с массами в диапазоне 109 + 1О11М0, как, например, сверхмассивная Черная Дыра SDSS J140821.67+025733.2 в центре квазара SDSS J140821, имеющая массу 1.96 • 1О11М0.

Считается, что сверхмассивные Черные Дыры с массой ~ 1О9М0 являются центральными объектами светящихся квазаров, наблюдаемых при красных смещениях z > 6, но их астрофизическое происхождение остается не до конца, попятным. В настоящее время открыто более 200 квазаров с z > 6 и несколько объектов с z > 7. Квазар с наибольшим iерасиым смещением при z = 7.5. что соответствует возрасту Вселенной в 650 млн лет, имеет абсолютную светимость 1,4^1047 erg/sec, при этом оценка массы по скорости движения газа в квазаре дает величину 1, 6±0, 4-109М0 [5]. Эти наблюдательные данные ставят вопрос о механизме образования и быстрого роста, таких объектов в ранней Вселенной.

Результаты численного моделирования [6] налагают ряд ограничений на. параметры образования сверхмассивиых Черных дыр. Так, например, показано, что легкие зародыши Черных Дыр с массой М ^ 103М0 даже при сверхкритической аккреции не могут вырасти до масс порядка 108 М0 и a z = 6. Для образования сверхмассивиых Черных Дыр с массами 108 + 109М0 необходимы более тяжелые зародыши М ~ 104 + 106 М₀ и богатые газом галактики, содержащие квазары. Однако, в настоящее время пет достаточно убедительных моделей появления таких тяжелых зародышей в ранней Вселенной. Кроме того, было обнаружено, что пространственная плотность светящихся квазаров быстро уменьшается с увеличением красного смещения, причем эта. тенденция усиливается за пределами z = 5 + 6 [7].

Интерес к механизмам образования сверхмассивиых Черных Дыр с учетом факта доминирующего присутствия их в составе квазаров, вызван, в частности, тем обстоятельством, что такие Черные Дыры формируются в составе квазаров на. достаточно ранних стадиях эволюции Вселенной, до образования звезд. Это обстоятельство, в частности, открывает возможность формирования сверхмассивиых Черных Дыр в условиях, когда, существенное влияние на. этот процесс могут оказать скалярные поля и барионная темная материя. В связи с этим отметим работы [8], [9] и [10], в которых рассматривается возможность существование скалярных гало и скалярных волос в окрестности сверхмассивиых Черных Дыр.

В [11] на. основе исследования систем скалярио заряженных вырожденных фермионов с фантомным взаимодействием было сформулировано следующее предположение: 1). холодная полностью вырожденная Ферми - система, с очень большими эффективными массами скалярио заряженных фермионов может стать хорошей моделью темной материи; 2). на. определенном этапе космологической эволюции гравитационные неустойчивости в иерелятивистской материи могут привести к возникновению обособленных областей с темной материей; 3). стандартные куперов-ские механизмы в Ферми - системах с отталкиванием одноименно заряженных частиц могут привести к образованию бозонов из пар фермионов и, тем самым, - к сверхтекучести областей темной материи; 4). при росте эффективных масс фермионов в растущем скалярном поле выше план-ковского значения массивные фермионы могут могут образовать устойчивые первичные Черные Дыры в варианте со сверхтекучими квази-бозоиами с пулевым спином.

В [12] - [13] на. основе развитой теории неустойчивости одпокомпопептпой системы скалярио заряженных вырожденных фермионов с синглетным Хиггсовым скалярным взаимодействием в так называемом жестком ВКБ -приближении было подтверждено предположение о неустойчивости коротковолновых возмущений. Эти предварительные исследования показали необходимость всестороннего и более глубокого изучения статистических систем скалярио заряженных частиц.

Далее, в [14] были предложены две наиболее простых модели взаимодействия фермионов с асимметричным скалярным дублетом: в первой модели такое взаимодействие осуществляется двумя типами разносортных фермионов, один из которых является источником канонического скалярного поля, а второй - фантомного (модель M1); во второй модели имеется один сорт фер- мионов, обладающих парным зарядом - каноническим и фантомным (модель M2). Там же был проведен и качественный анализ динамической систем модели M1. В работе [15] было проведено численное моделирование космологической модели M1, на основе которого выявлены особенности этой модели, в частности, возможность существования фаз космологического сжатия, осцилляции параметра. Хаббла, а. также возможность вселенных с конечным временем жизни.

Заметим, во-первых, что в случае космологической модели, основанной па классическом вакуумном скалярном синглете параметр Хаббла, является певозрастающей функцией времени (Н < 0)¹. При этом инфляционные решения Н = Const возможны лишь при постоянных значениях потенциала, скалярного поля, соответствующих точкам устойчивого равновесия динамической системы. Однако, оказываются, что такие решения устойчивы лишь по отношению к бесконечно малым возмущениям. Как показано в [16], а. также более детально - в [17] и [18], даже очень малые, по конечные, отклонения значения скалярного потенциала, от равновесного значения приводит к неустойчивости инфляционных решений и к переходу космологической модели па. стадию сжатия. Добавление в космологическую систему фантомного поля стабилизирует эту неустойчивость и поддерживает режим устойчивого космологического расширения [16]. Поэтому, несмотря на. известные энергетические и кваптовополевые проблемы с синглетным фантомным полем (см., например, обсуждение этого вопроса, в [18], а. также цитированную там литературу), мы включаем фантомное поле в исследуемую ниже модель. При этом переход к синглетной модели, основанной на. чисто классическом либо чисто фантомном поле, управляется параметрами модели, которые для теоретической полноты сохраняются нами произвольными, что позволяет выявлять особенности воздействия компонент модели на. ее свойства.

Во-вторых, заметим, что мы рассматриваем модель без излучения, в которой материя представляется холодной вырожденной системой скалярио заряженных фермионов и соответствующими этим зарядам скалярными Хиггсовыми полями. Такую холодную систему фермионов можно рассматривать в качестве модели темной материи на. ранних стадиях эволюции Вселенной. В данной работе мы исследуем гравитационную устойчивость модели M1 двухкомпонентной статистической системы с асимметричным скалярным взаимодействием фермионов, снимая условие жесткого ВКБ -приближения [12] - [13], и проведем сравнение с результатами предыдущих исследований.

А. Математическая модель двухкомпонентной системы вырожденных фермионов с асимметричным скалярным Хиггсовым взаимодействием

В [14] показано, как па. основе Лагранжева, формализма, из микроскопических уравнений движения скалярио заряженных частиц можно получить макроскопическую модель статистической системы скалярио заряженных частиц, описываемую макроскопическими потоками. В данной статье мы воспользуемся результатами, полученными в [14].

Ниже мы будем рассматривать космологическую модель, осиоваииую на. двухкомпоиеитиой вырожденной статистической системе скалярио заряженных фермионов и асимметричном скалярном Хиггсовом дублете, состоящем из канонического скалярного поля Ф и фантомлого поля p [14]. Согласно [14] динамические массы m_z и т^ ферм ионов ги (с зарядами e_z и е^ по отношению к каноническому полю Ф и фантом!юму полю p описываются формулами:

m_z = e_z Ф, т^ = е^ р. (1-1)

Функция Лагранжа L_s не взаимодействующих между собой скалярных Хиггсовых полей асимметричного скалярного дублета, есть

^Ls = ^LФ + ^L_v = тх— (д^гкф,г^ф,к ^{— 2} С^(ф)) + —— ^(— д^{гк р}у^рд ^— 2V^(p)), (1.2) 16^ 16^

где

Ф   -1 (Ф2- т)2; г(Ф) = - f (д — mУ                (1.4)

- потенциальные энергии соответствующих скалярных полей, a,f- константы их самодействия, т, m - их массы квантов. Тензор энергии - импульса скалярных полей относительно функции Лагранжа (1.2) есть:

Т^ к = Т ( ф) к + Т_{Ы к} = 1^ (2Ф^,гФ,к5кФ,,Ф,' + 2Г(Ф)5к) + 1^ (_<-2^_ч >- ^г_ч>^_k6ⁱ_kЧ > _dЧ >'^ + 2Г(.)5к), (1.5)

Далее, тензор энергии - импульса, равновесной статистической системы равен:

Т(р)к = (еР + Рр)^^к - Ур,(1.6)

где мк - вектор макроскопической скорости статистической системы.

Уравнения Эйнштейна для системы “скалярные поля—частицы” имеют вид:

Кк - 2^Я  -т. + 5кЛо,(1.7)

где грк _ грк тк т (з)к + т (р)к,

Ло - затравочное значение космологической постоянной, связанное с ее наблюдаемым значением

Л, получающимся при изъятии постоянных слагаемых в потенциальной энергии, соотношением:

Л = Ло

1 \ е тТ

4 -^ а_т т

(1.8)

Строгими макроскопическими следствиями кинетической теории являются уравнения переноса, в том числе закон сохранения некоторого векторного тока, соответствующего микроскопическому закону сохранения в реакциях некоторого фундаментального заряда Q с мультизарядами частиц q^ - vk Е qTa* = о,                           (L°)

а

• а. также законы сохранения энергии - импульса, статистической системы:

v^ - Е°^т v⁽ Фт = 0,                         (1.10)

т где от - плотность скалярных зарялов по отношению к полю Фт [19].

Из соотношения нормировки вектора, скорости вытекает известное тождество иккНк = 0,                                           (1.11)

которое позволяет привести законы сохранения энергии - импульса. (1.10) к виду уравнений идеальной гидродинамики

(Ер + Рр)иг,кик = (дгк - uV) ^Рр,к + Е °ТФт,к^ ; Vi [(Ер + Рр)ик] = ик (рр,к + Е ^ТФт,к^ , (1-12) (1-13) а законы сохранения фундаментальных заряда QT (1.9) к виду

V к p^тu^к = 0;

(г = 1,^),

(1.14)

где

Р^Т = ^ ^Да)                          (^1Л5)

• - кинематическая плотность скалярного заряда статистической системы по отношению к скалярному полю Ф_г.

Макроскопические скаляры для двухкомпопептпой статистической системы вырожденных фермионов принимают вид:

4 4Ф4"4 Д еР =     F2^z ) + ^—2 F2^c)(

4 4Ф46

Р р = ^№ф ) - 4F1(фz)) +    №(ф_с) - :/ .));                (1.17)

24—224—

• 4 4Ф3               г"4

°z =    Fi(^z);    ' = S" ^), где crz ист’- плотности скалярных зарядов "z и 6’ и

Фz = ^—_а,;      ф< = ^—'.                                   (i-i9)

|"z ф|                  |"’ ,|

Для сокращения письма введены функции F1(ф) и F2(ф):

Fi(ф) = ф^1 + ф2 - 1п(ф + V1 + ф2);                       (1-20)

F2(ф) = фV1 + Ф2(1 + 2ф2) - 1п(ф + Vl+ф).                  (1-21)

Функции F1 (ж) и F₂(ж), во-первых, являются нечетными:

^Fi^(-ж) = ^{- F}i⁽x); ^F2^(-ж) = ^{- F}2^(ж),                           (1-22)

а, во-вторых, имеют следующие асимптотики

2 ^^1(ж)|ж^0 - 3ж	3; F2'.2) ,/ZI-	8 ж3; 3 ;
№(ж) -	4^1(ж))..   .-	8ж5; 5 ;	(1-23)
1||.г: .;..±х-ж|ж|;	^2(ж) ,...:ч	— 2ж3|ж|.	(1.24)

Выпишем также полезные для дальнейшего выражения для производных функций F1(ж) и F2(ж):

• .             2ж²            .             „ ,--------- d . /---------        „ , --------- ж⁴

F1(ж) = .      ; F2 (ж) = 8ж² у/1 + ж²; — ж³ V 1 + ж² = 3ж² V 1 + ж² +— ^      .     (1-25)

V 1 + ж2                          дж                            у 1 + ж2

Наконец, уравнения скалярных полей для двухкомпопептпой системы принимают вид:

• □Ф + т²Ф - аФ³ = ^"ZФ⁴F₁(ф_z),                           (1-26)

—2

• -□, + m², -ф,³ = --^б4^⁴^(фг).                          (1-27)

—2 ’

• В.    Линейные плоские возмущения космологической модели

ВЛ. Невозмущенное изотропное однородное основное состояние

В качестве фоновой рассмотрим прострапствеппо плоскую метрику Фридмана.

dso = о (^)(д^ — дж — ду — dz ) = dt — о (Д(дж + dy + dz ),            (2.1)

где космологическое время t связано с временной переменной ту соотношением t =

j a(-i]W

(2.2)

а. в качестве фонового решения рассмотрим однородное изотропное распределение материи, в котором все термодинамические функции и скалярные поля зависят только от времени:

5'0 :   Ф = Ф(t); ф = ф(t); т z = т z(t); т ^ = т ^(t); и2 = ^(t).(2-3)

Нетрудно убедиться, что иг = 54(2.4)

обращает уравнения (1.12) в тождества, а. система, уравнений (1.13) - (1-14) сводится к 3-м материальным уравнениям:

Ер + 31 (ер + Рр) = crz Ф + сг^ ф;(2.5)

а ти + 3-ти = 0,                                          (2.6) а пс +3 |пс = 0.                                       (2.7) где ф = dxj)/dt. В [14] показано, что система уравнении (2.5) - (2.7) имеет простые решения:

ат2 = const;     ат^ = const.                                (2-8)

С учетом (2.8) и (1.1) запишем безразмерные функции ф₂ и Ф (1-19) в явном виде:

т0                т0 Ф= = «|еЛ|'' ф = *Ф|'     ('^ = ’(“)(0))-                   1291 где мы перешли к новой переменной ^(t)

£ = ln а,                                            (2.10)

полагая здесь и в дальнейшем

€(0) = 0.                                               (2.11)

Далее, тензор энергии - импульса, скалярного поля в певозмущеппом состоянии также принимает вид тензора, энергии - импульса, идеальной изотропной жидкости:

	Т* = ( е 8 + Ps>?uk - р8дгк ,                                (2.12)
причем:	1/1 ф2 — (22 £s      (2 а2 ф + V(Ф) + V (ф/;                            (2.13) P s = Г (1Ф ' - V (Ф) - V(ф)),                           (2-14) 8т у 2   а2
так что:	e Ф2 — ф 2 es+ P s =й       2   .                                       (2.15) 8т   а2

Уравнения певозмущеппых скалярных полей (1.26) - (1-27) в метрике Фридмана принимают вид:

<Ф + 3а + т2Ф - аФ3 = -8та2ст2,                              (2.16) ф + 3аф - т2ф + фф3 = 8та2ст^                           (2-17) а где плотности скалярных зарядов ст4 и ст4 описываются выражениями (1.18), в которые необходимо подставить значения функций ф4 и Ф4 (2.9).

Наконец, независимые уравнения Эйнштейна, пулевого приближения имеют вид (см. [14]):

^Н = -у + у   т— ^-4^Ф4ф3У¹ + ^ф2 ^- — ^-4^ф4ф3 J¹ + ^ф2;              (2-18)

2     2    ЗГ                      ЗГ ъ ъ V s

• _{2 А} Ф²     ф ²   т²Ф²    аФ⁴    т²ф²    Зф⁴    -4Ф⁴   , , .   -4ф⁴   , , .          ,    .

3Н² - Л - — +   --— + —---+   --- Р2(ф , ) -     Р2(ф ( ) = 0.   (2.19)

2    2      2      4      2      4 Г            Г где Н(ту) - параметр Хаббла,

Н = - = е                                 (2.20)

а

Таким образом, уравнения (2.16), (2.17), (2.22) и (2.20) относительно функций ^(t), Н (t), Ф(t) составляют полную систему обыкновенных дифференциальных уравнений, описывающих исследуемую певозмущеппую космологическую модель. При этом уравнение (2.19), как показано, например, в [14], является первым интегралом этой системы, с помощью которого необходимо определять начальное значение параметра. Хаббла, при решении задачи Коши. Система, уравнений (2.16), (2.17), (2.22), (2.19) и (2.20) исследовалась методами качественной теории дифференциальных уравнений в [14] и численными методами в работе [15].

Заметим, что указанную систему уравнений проще исследовать во временном масштабе физического времени t (2.2), поскольку относительно этой переменной полная автономная система уравнений космологической модели принимает наиболее простой вид [14]:

£ = Н;Ф = Z ; ф = z;                (2.21)

Н = - у + у - уе⁴Ф⁴ф^1 + Ф2 - уе⁴ф⁴ф3^1 + ф²;             (2.22)

2     2    ЗГ                      ЗГ ^{ъ ъ} V ^s

Z = -3НZ -m2Ф + Ф3 (а - 4-4К1(ф4/); (2.23) ;z = -ЗНг + т2ф - ф3^З--4^1(Фу)^ , (2.24) причем выражение для первого интеграла. (2.19) можно переписать в форме

ЗН 2 - Л - ^Z2 + z2 - ^Ф + 2     2      2

аФ4

т²Ф² Зф⁴

2 + Т

е ⁴Ф⁴           -4ф⁴

-4Г-^2(фг) - -^^(Фс) = 0.

(2.25)

• С.    Уравнения первого порядка по возмущениям

В дальнейшем, мы будем использовать и временную переменную у для адекватности стандартной теории возмущений Лифшица (см., например, [21]). В дальнейшем всюду с помощью /‘ будем обозначать производную по временной переменной у. При этом необходимо учитывать простые правила, дифференцирования ф = — ф'; ф = —‘‘Ф"--уф', ^ Ф' = аф; Ф = —'Ф + -аф а         а2      а3

и соотношение £' = аН.

С.1. Продольные возмущения

Метрику с гравитационными возмущениями запишем в виде (см., например, [21]):

ds² = ds^ - а² (y)h_a ^ dx^adx ^ ; ds^ = а (y)(dy — dx — dy — dz ).

(3.1)

Обращаем внимание на конформный множитель —o²(q) перед ковариантными амплитудами возмущений, который пропадает для смешанных компонент возмущений h^. При этом ковариантные возмущения метрики равны:

59<хр     о (^^^р -(3-3)

Далее:

^h P = ^h7^ 9 q⁷ = ^— .2 ^h “S ^;                              *'²"^*

h = ha = 3o^ haP = — 02 (h11 + h22 + h33).(3-5)

В дальнейшем будем рассматривать лишь продольные возмущения метрики, имея ввиду задачу о гравитационной устойчивости плоских возмущений, для определенности направляя волновой вектор вдоль оси Oz. В этой системе координат hii = h22    ..'^ '■.,■■ ■;

h = ^(f)e^mz ; hi2 = his = h23 = 0;

h33     ..' -: • . . • ,     .(3.0)

Как видно из предыдущих формул, материя в пашей модели полностью определяется четырьмя скалярными функциями - Ф(z,q), ^(z,q'), ^_z(z,q') и т^-(z,q) и вектором скорости и^г (z,q) Следуя [12], разложим эти функции в ряд по малости возмущений относительно соответствующих функций на. фоне метрики Фридмана. (3.2):²

Ф(z, q) = Ф(7) + 5Ф(q)e^гnz;     ^(z, q) = ^(q) + 5^(q)e^mz ;

^ z (z,t) = ^_z (q)(1 + 5_Z (q)e^mz ); m_c (z,t) = m_c (q)(1 + 5 _c (q)e^mz );                  (3.7)

a^z (z, q) = a^z (q) + 5a^z(q')e^lnz ; ct ^ (z, q) = ct ^ (q) + бст ^ (q)e^mz;

Ф = 0 54 + 53 n(q)emz, где 5Ф(7), 5^(q), 5z(q), 5^(q), sz(q^s^(q) и v(q) - функции первого порядка малости по сравнению с их невозмущенными значениями.

С.2. Уравнения возмущений скалярных полей

Разлагая в ряд Тейлора, уравнения поля (1.26) - (1.27) по малости возмущений, получим уравнения для возмущений скалярных полей первого порядка 5Ф, 5^:

5Ф" + 2 — 5Ф' + [п² + о²(т² - 3оФ²)]5Ф + |ф'Д = - 8^o²5a^z ;                (3.8)

5^" + 2 — 5^' + [п² — о² (m2 + 3^ф²)]5ф + | ^ Д' = 8 ^o ² 5ct ^ .                (3.9)

Эти уравнения отличаются от аналогичных для возмущений вакуумных скалярных полей лишь членом с источником скалярного поля в правой части и знаками в кинетических членах для фантомного поля (см. [20]).

С.З. Уравнения для гравитационных возмущений

Разлагая теперь уравнения Эйнштейна. (1.7) в ряд Тейлора, по порядкам возмущений (некоторые детали см. в [12], [20]), получим следующие независимые уравнения для гравитационных возмущений возмущений первого порядка /,А:

у = -—■■'"'.    f ^8ФФ‘^{— 5}w‘ ⁺ 1^(А‘ ⁺ /‘));

(3.10)

(3.11)

(3.12)

(3.13)

8т тй ³ ( е + р)р\                3         /

8тга²58 р = —р‘ — Ф‘8Ф‘ + ^б^ + ^- (А + /) — а²(т² — аФ² )Ф8Ф — и² (m2 — У^²)^8^; а                       3

А’ + 2 ^А’ — |п²(А + /) = 0;

/‘ + 2— / + -п²(А + /) + 38Ф‘Ф‘ — Збр’р’ —

— 3а²[Ф8Ф(т² — аФ²) + рбр(т² — У^²) — 8^8р_р] = 0.

Можно показать (см., например, [14]), что дифференциально - алгебраическими следствиями уравнений (3.10) - (3.13) являются уравнения для возмущений скалярного поля (3.8) -(3.9) и уравнения движения первого приближения вырожденной материи. Последние, очевидно, являются излишними, так как возмущения скорости и плотности энергии материи непосредственно определяются уравнениями (3.10) и (3.11). Из оставшихся уравнений мы выберем 4 независимые: (3.8), (3.9), (3.12) и (3.13) для того, чтобы максимальным образом приблизить математическую модель к стандартной теории Лифшица. При этом уравнение (3.12) совпадает с соответствующим уравнением теории Лифшица, а. уравнение (3.13) отличается от соответствующего уравнения работы [20] лишь материальным членом 8р_р и добавлением аналогичного члена для фантомного поля.

Заметим, что в отсутствие фермионной системы е_р = 5е_р = р_р = 5р_р = 0 выражение в скобках правой части (3.10) обращается в пуль и дает уравнение на. возмущения полей и метрики, как и уравнение (3.11) вместо определения возмущения плотности энергии фермионной компоненты становится уравнением на. эти возмущения. В [20] показано, что не все уравнения на. возмущения вакуумных скалярных полей и возмущений метрики независимы, а. в [22] найдены ВКБ - решения соответствующих уравнений для возмущений классического скалярного поля. Поскольку система, уравнений для возмущений вакуумных скалярных полей принципиально отличается от системы уравнений для возмущений полей с источниками, в дальнейшем мы будем предполагать обязательное наличие фермионной компоненты и, тем самым, - выполнение условий:

е_р Д 0; 5е_р Д 0.                                      (3-14)

Вводя новую переменную для гравитационных возмущений v = А + /                                     (3.15)

и складывая обе части уравнений (3.12) и (3.13), получим вместо этих двух уравнений новую систему уравнений относительно переменных А и v

А’’ + 2 —А' — 1n²v = 0; (3.10 а 3

v‘‘ + 2^—v‘ + |ⁿ2v + 38Ф‘Ф‘ — 3бр‘р‘ — 3а²[Ф8Ф(т² — аФ²) + ^8^(m² — У^²) — 8^8р_р] = 0. (3.17)

Для замыкания системы уравнений необходимо найти связи между возмущениями макроскопических скаляров, с одной стороны, и возмущений скалярных и гравитационных полей, - с Другой.

С.4. Возмущения фермионной компоненты

Найдем теперь указанную выше явную связь макроскопических скаляров вырожденной Ферми - материи с возмущениями скалярного и гравитационных полей. Учитывая формулы (1.6), верные для идеальной жидкости (см. [21]), и представляя возмущения импульса. Ферми в виде

6^ = ^_г 5_Z Me^mz;     5^_с = ^_с 8_С Me^mz,                      (3.18)

запишем возмущение макроскопических скаляров в первом по возмущениям приближении:

5ti _z = 3n_z (t)5_z (t')e'¹

,гтгг.

5п с = 3n ^ (t)5 ( (t)e'

;

.^z.

;   5^ z = ^ Z (n)7 z (**";

; ^5ф с = ^фс ⁽rhc ⁽n^)eMz ,

(3.19)

где согласно (1.19)

^z У

^_z (п)      , / x       ^C (п)         , x     ^(п)       / X

^; фс⁽ⁿ⁾ =            ^{; n} z ^(t) =     2 ^{; n} C ^(t)

|ez Ф(п)|              |еспп)|               ^2

Д3М v ²

(3.20)

и введены возмущения приведенного импульса Ферми pj(т для каждого сорта фермионов

7z (п) = 5, (п)

^Л);  7с (п) = ⁵ C (п)

Ф(Ч)

M^) vM '

(3.21)

Кроме того, из законов сохранения зарядов ez и ес (1.12) с учетом (3.7) мы можем получить законы сохранения числа, каждого сорта, фермионов в первом порядке теории возмущений

- р' + 35' + гпи = 0, 2

- р + 35’ + гпи = 0,

откуда, сразу следует:

5z = 5с = 5;                                         (3.22)

- р‘ + 35' + гпи = 0,                                      (3.23)

т.е., относительные возмущения импульса. Ферми вырожденных фермионов совпадают. При этом уравнение (3.23) является альтернативным (3.10) определением скорости возмущений и. Заметим, что оба. эти уравнения получены как законы сохранения из уравнений переноса. - уравнение (3.23) получается из закона сохранения заряда, а. уравнение (3.10) - из закона, сохранения энергии-импульса. статистической системы. В [14] показано, как закон сохранения энергии фермионов получается из закона сохранения заряда. Таким образом, скорость возмущений Др) определяется алгебраически через любую из указанных формул. Итак, формулы (3.24) принимают вид:

7z ⁽Ч) = ⁵⁽п) ^-

5Ф(п)

Ф(Ч) ;

7C ⁽Ч) = ⁵⁽п) ^-

Мп) Hr)

(3.24)

Далее, с учетом дифференциальных тождеств (1.25) найдем выражения для возмущений макроскопических скаляров фермионов (в соответствие с замечанием на. стр. 71 ниже мы опускаем экспоненциальный множитель emz):

43 Saz - ezz^r	(3Fi(^z) -	ф3   )5ф	3 ^ z 5	;                           (3.25)
2V2		-1 + Ф27 ф	-1 + Ф2
r   ebp3 5^C = -Г7Т 2 v 2	(3Fi(^c) -	Ф3  ) 5p + ^1 + Ф2^ p	Ф3 , C 5 V1 + Ф2	;                          (3.26)

'  = ^(Д)5Ф + ес|г^1(фс)5v + ^ ^Ф4Д-1 + Ф2 + е^4ф3^1+<)5;

(3.27)

⁵Р р

4 ⁴Ф³              e4v3               1 ( . л У

. ^{: ф +} ..Л . ⁺ 3^2 ф^ф4-^

+ еС^4        )

^ 1 + ф| 7

5,

(3.28)

где

X3

F 3 ( t ) =          + ln(x + у/1 + x²) > 0.

V1 + x2

В итоге, все возмущения макроскопических скаляров для вырожденной плазмы полностью определяются тремя функциями возмущений: 5Ф(т), 5р(т) и 5(т).

Таким образом, подставляя выражения для макроскопических скаляров (3.25) - (3.28) в уравнения скалярных полей (3.8), (3.9) и уравнения Эйищтейиа (3.11), (3.16) и (3.17), мы получим искомую замкнутую систему пяти обыкновенных дифференциальных уравнений второго порядка, относительно пяти функций возмущений: 5Ф(т), 5<р(т) А(т), Дт) 5(т)- При этом специфика переменной 5 (т заключается в том, что эта переменная входит в уравнения линейным алгебраическим образом, что позволяет, в принципе, исключить ее через одно из уравнений и, тем самым, свести исследуемую систему к системе четырех дифференциальных уравнений относительно четырех функций 5Ф(т), 5р(т), А(т), ЛтУ Проще всего это сделать, подставляя выражение (3.27) в уравнение Эйнштейна (3.11), найденное выражение для 5(т) подставить в скаляры s^z (3.25), s» (3.26), 5р_р (3.28), а затем в исследуемые уравнения (3.8), (3.9) и (3.17). Мы, однако, не будем выписывать полученные таким образом уравнения вследствие их чрезвычайно громоздкого и малополезного вида.

• D.    ВКБ-приближение

D.I. ВКБ-приближение, размерность

Проведем размерностный анализ исследуемой динамической системы (3.8), (3.9), (3.11), (3.12) и (3.13). Из (1.1) следует, что величины q^r ф, имеют размерность массы³

[егФ] = Д] = [н] = [I] ,(4.1)

где [А] означает размерность величины А, а I здесь и в дальнейшем означает масштаб длины. Далее

M = ^.y.z] = № [а(т)] = [1]; [п] = [1 ] .(4.2)

Тогда, например, из уравнения Эйнштейна. (2.19) следует:

[Л]= [4] ; [Ф,^] = [1]; [«.^]= [4] ; [=,.«(]= [^_] .(4.3)

Далее, из определения (3.1) следует, что возмущения метрики являются безразмерными функциями, как и возмущения скалярных полей. Из определения возмущения импульса. Ферми (3.18) следует, что 5(т) также безразмерная функция. Таким образом, все возмущения безразмерны:

M = W = [^ ] = [5Ф] = 5[р] = [5] = [1].(4.4)

Будем полагать характерный масштаб неоднородности фона порядка I = т а'

∼ а

т ’

ф'

∼ ф

т ’

р ^ 1 р т

.

(4.5)

Исследуем сформулированную математическую модель космологической эволюции возмущений (3.8), (3.9), (3.11), (3.12) и (3.13) в коротковолновом секторе возмущений (см., например, [21])

пт ^ 1 ^ 5Ф' ~ п5Ф ^ —5Ф ~ — 5Ф;.   5^ ~ п5р ^ — 5р. ~ — 5Ф;

и т.д.

В соответствие с методом ВКБ представим решения уравнений /(т) в форме / = /(т) • ■^“(^;  (|«|~п > 1).

(4.6)

(4.7)

где /(т) и и(т) - слабоменяющиеся наряду с масштабным фактором функции амплиуди и эйконала, возмущения.

D.2. ВКБ-решения волновых уравнений

Для того, чтобы не возвращаться всякий раз к вопросу ВКБ-приближепия, продемонстрируем технику решения уравнений в ВКБ-приближепии па. примере нахождения ВКБ-решепий волнового уравнения относительно скалярной функции Ф(г,т)

□Ф = 0.

(4.8)

В дальнейшем мы будем обращаться к полученным ниже ВКБ-решепиям волновых уравнений, как к базовым. Представляя Ф в форме (4.7), получим из (4.8) уравнение:

□Ф = 4 Цп² - и²)Ф + iu' Ф + 2шФ' + Ф" + 2- (шФ + Ф')] e^{i 4} Ч^ = 0. а²                                         а

(4.9)

Отделяя порядки ВКБ-приближепия чим уравнения:

в (4.9) и ограничиваясь первым приближением ВКБ, полу-

0-й порядок

4^(т2 а²

- и2)Ф = 0;

1-й порядок

м

~

а и'Ф + 2иФ' + 2—иФ

а

)=0.

Из уравнения нулевого приближения найдем и = ±п. Подставляя это решение в уравнение первого приближения, найдем Ф = соп8Ь/а(т) и, таким образом, найдем ВКБ-решение волнового уравнения (4-8)

Ф(2,т) - ^ (*±\

(4.Ю)

а которое описывает запаздывающую и опережающую волну, распространяющиеся со скоростью света.

Рассмотрим теперь волновое уравнение для массивного вакуумного скалярного поля

□Ф + т2(т)Ф = 0.

(4.11)

апало-

где массивный член также является медленно меняющейся величиной т' ~ m/т- Поступая гичпо предыдущему, получим вместо (4.9) следующее уравнение

□Ф + т2Ф = — (n2

а

- и² + а²т²)Ф + iu' Ф + 2iuФ' + Ф'' + 2 —(iuФ + Ф')

eij u⁽r) ) dr) = о.

(4.12)

Учитывая тот факт, что величина а(т)т(т) с увеличением времени может стать порядка и даже больше п, мы должны удержать этот член в уравнении нулевого порядка. Таким образом, имеем уравнения в первом ВКБ-приближепии

0-й порядок

1-й порядок

4^(т2 а²

— и2 + а2т2)Ф = 0;

~

а и'Ф + 2иФ' + 2 — иФ

а

) = 0.

откуда, для пулевого ВКБ-приближепии найдем:

и = ± V п² + а² m2 .

(4.13)

Подставляя решение (4.13) в уравнение первого ВКБ-приближепия, легко найдем

Ф(г, j) —

п

а(п2 + а2т2)1/4

inz ± i [ Vn² + а²m² dj e

.

(4.14)

Поскольку частотой волны ш в полученном решении служит подынтегральное выражение в экспоненте (4.14), определим стандартным образом⁴ фазовую v j и групновую v_g скорость волны:

ш(п)      I    а^т2 v j =      = А / 1 +       > 1; п           п2

Эш(п)          1 V g = я = /---------- < 1-               (4.1о) дп          а2 т2 N 1+ п2

D.3. ВКБ-решения для уравнений связи

Заметим, что, в отличие от переменных 5Ф(ту), 5у(ту), А(ту) и v (ту) переменная 5(ту) входит в динамические уравнения лишь алгебраически, что позволяет сократить число динамических функций до четырех. Для нахождения 5(ту) можно воспользоваться уравнением Эйнштейна (3.11), в левую часть которого необходимо подставить выражение 5е_р из (3.27). и согласно ВКБ-приближению отбросить в этом уравнении связи малые величины порядка пЦ^. В результате при выполнении условий (3.14) получим алгебраическую связь:

5 =

у v - а2[(ер + т2Ф - аФ3)5Ф + (е* + m2^ - 3^3)5^] 8/а2 ер

(4.16)

п2

=      v

24^а2Е4

Др5Ф - Д*5^; (5е_р Д 0),

где введены обозначения:

еР = /2 (-4Ф4* 3 V1+^2 + -( Л* 3 ^/1+^2} > 0;

.    е^{4 3}                  -4^3                    еФ               е *

(4.17)

еФ =  ^  '); е* = > W();   ^Д ф =    ; ^Д* =    -

Zj /                        //I                        ОМРр             ОМРр

Заметим, что все коэффициенты в линейной связи 5(v, 5Ф, 5^) являются безразмерными величинами, при этом величины ер, е р и е* имеют размериость I^-2.

Далее, полученное выражение для 5 (4.16) мы должны подставить в выражения для возмущений скалярных плотностей заряда s⁴ (3.25) и s⁽ (3.26), а также в выражение для возмущения давления статистической системы (3.28). Полученные таким образом выражения мы должны, в свою очередь, подставить в соответствующие уравнения для возмущений скалярных полей (3.8) и (3.9) и уравнение Эйнштейна, для возмущений (3.17). Таким образом, получим, например:

5а⁴ = -----⁴ f ⁴     n²v + S| 5Ф + S⁴ 5^;

(4.18)

48/3й2ерЛ1+Л1      Ф с 4

Sp

л* >-

f3

f2

y/T+fi  0Tf2

Дф) ;   S * =

-4 Ф- ■ д . 2/2^1+^ *^;

5^ ^ =---- ^{- с} ^ ^{f z}     n²v + S< 5Ф + S*5^;

48/3а2ер у 1 + f 2

(4.19)

⁵Р р

Р⁵ р

S *

42              3

-1^ |3Г1(*() -

2/  \       Vi+fl

р Р п²

24/3а2еР

v + Р ^Ф5Ф + P * 5_V;

Л ( -4Ф4*4 , -W4 А

/² VVi+fl⁺ yr+f² ) >  ^;

*2

((

/-------^ *;

Д+Д)

-^Р1(^4 ) -РрДр;

2/2

------,        ДФ;

2/2 ^1 + f 2

(4.20)

р * =          ) -РрД*-

2/2

Заметим, что все коэффициенты в линейной связях 5cr^2,s(v, 5Ф,5ф) и 5p_p(v, 5Ф, 5ф) имеют

размерность I 2. а рР является безразмерной величиной.

D.3.1 Асимптотические значения функций (4.17) — (4.20)

В дальнейшем нам понадобятся асимптотические значения функций (4.17) - (4.20) в нерелятивистском (и,. ^ 0) и улътрарелятивистском фф_Т ^ то) пределах. Заметим, что эти пределы эквивалентны также большим и малым, соответственно, значениям зарядов, или малым и большим, соответственно, значениям импульсов Ферми. Используя соответствующие асимптотики функций (1.23) и (1.24), получим следующие асимптотики.

Нерелятивистский предел i r ^ 0 О большие заряды |er| ^ тг_г

^еР ^ -2(|е_г^ф|т3 + |е₍ф^); рР - -2^(т4 + ^т(); е_р -    ^sg^n(ф)т3; е* -    sgn(^⁾773;

^Р т^{2                    s Р}   т²         S ^Р    3т^{2              Р}    3т²         s

△ ф —

|е?|sgn(Ф)т³       ; ^__ ^|е(^|sgn(Ф^)т3       ; „?__ |е?|³т5       sgn(Ф) ;

24т(т3|е?Ф| + т3|е(ф|ф *    24т(т3|е?Ф| + т3|е(ф|ф ф      596т3 т3|е?Ф| + т3|е(ф|’

s Q* —	|е( |3т5 596т3 т3	sgn(i)      ; Qs — . |е?Ф| + т3|е(ф| ’ ф	- е2|е? |т2т3 4т2	sgn(<); Q* —	е2|е(|т2т3      , . 4т2    sgnCi);
			Р ф — J	1 е? |т3 2 sgn(<) : 3т2	|е( |т3 Р* —„ Csgn(i)(4.21) 3т2

Ультрарелятивистский предел i r ^ ^ О малые заряды |er| ^ rr

еР— 4(т4+ т<); рР - 11 е ■ф|т3+ Kiki);еф — егфт2;е* — уФт2; Р   т2        s Р   т2                         Р    2т2      Р    2т2 s е 2фт2              е2фт2               |е3|Фт, ,    |е3|фтг

; △ ^{s s} ; Q?^т^_ ; Q^{S       s} "     •

2(т4 +т44)    *    2(т4 +т44)         4т2(т4 + т()    * 4т2(т4 +т44)

|е3ф|е2Фтлт2            |е3Ф|е2фт2т2

( _— - (T ? ^{s 2} ; „_{z —} - Z ^{(   2 (} ;

^ф 4т²(т4 + т() ’   *      4т²(т4 + т() ’

р * ₌ е!М_{; Р}^ еИ 2т²            2т²

(4.22)

D.4. Уравнения для возмущений в терминах ВКБ

Представляя, например, 5Ф(^) в форме (4.7), найдем:

5Ф(^) = 5Ф(^) • е® -Ь^ ;  5ф‘ = [5ф‘ ₊ ^ф]е« /“(^)^^;

5ф" = [5ф‘‘ + 2ш5Ф‘ + гаФФ - и²5Ф] е^{г - u(}^^)d^                   (4.23)

Подставляя полученные выражения для возмущений макроскопических скаляров (4.18) - (4.20) в уравнения для возмущений скалярных (3.8), (3.9) и гравитационных полей (3.16) и затем подставляя возмущения 5Ф, 5р, v и А в форме (4.7) в переформулированную систему (3.8), (3.9), (3.16) и (3.17), с учетом соотношений (4.23) получим систему обыкновенных дифференциальных уравнений относительно амплитуд 5Ф, 5(р, z>, А и функции эйконала м(^).

е4Ф3^2

[п² - U² + а²(т² - 3аФ² + 8т5'|)]5Ф +-- ² , ^Z     u?v - 8тй²^?5<^

6т2еР у/Г+ф2           *

(4.24)

й        1                           й

+г [2м5Ф‘ - мФФ + 2—м5Ф - -Ф‘и(А - р)] + 5Ф +2 — 5Ф‘ -

1<У = 0;

е4^3ф2

[п² - и² - a²(m² - 3Рр² + 8т5'*)]5<р--- — ^    n²v + 8та²5'ф5Ф

6т2еР yi + ф2

(4.25)

+г [2и5<)5‘ -

а' _        1

и'Sip + 2— и&<р - -^'и(А - v)l + а 2

6ф" + 2 ^й- бф* -а

1 га, 2фМ

= 0;

—и2А — дП2т> + г [2иА‘ — и’А + 2—иА] + А + 2— А' = 0;               (4-26) [п2 (1 + 1 1 ) — и2] V — 3а2[Ф(т2 — аф2) — 8^Р Ф]^Ф — 3а2[ф(т2 — фф2) — 8гР ^]5ф     (4.27) +г [2иР‘ — и' v + 2— u V + 3и5ФФ‘ — 3и5фф] + |^Д’’ + 2—/7‘ + ЗФФФ ‘ — Зф’Фсф’] = 0.     (4.28)

Е. Решение уравнений для возмущений методом ВКБ

ЕЛ. Дисперсионное уравнение: нулевой порядок ВКБ

Уравнения (4.24) - (4.27) в пулевом порядке ВКБ представляют систему однородных алгеб раических уравнений относительно амплитуд возмущений:

A·

~

ф

ф

~

А

V

= 0,

(5.1)

где A - квадратная матрица размерности 4

A =

Р.4Ф3-1/;2

п ² — и ² + a ² ( m ² — 3 а Ф ² + 8"к8» )   — 8 га ² S2                         0     ------- п ²

^ф         ^                          6 ^2 4 у т+Ф ²

8 ^a 2 s ф	п 2 — и 2 — а 2 ( т 2 — 3 3у 2 + 8 ^S ^, )	0	е 4 ^ 3 ^ |      9 ---— - 4    п 2 6 ^ 2 е ^ J1 + ф |
0	0	— и 2	— 1 п 2 3

— 3 а ² [Ф( т ² — а Ф ² ) — 8 ^Р ^ф ]         — 3 а ² [ ^ ( т ² — 3^ 2 ) — 8 ^Р ^ ]

⁰    ( 3+58— и 2

(5.2)

Необходимым и достаточным условием нетривиальной разрешимости системы (5.1) является равенство нулю определителя матрицы A:

det(A(u, п)) = 0.

(5.3)

Решением дисперсионного уравнения (5.3) являются 8 симметричных функций эйконала. ±и(_к)(п, ту), (к = 1..4)⁵, последовательная подстановка которых в уравнения (5.1) даст нам фундаментальное решение (Ффп), ффп), Афтг), тгифтг)). Полученные алгебраические решения затем необходимо подставить в дифференциальные уравнения первого порядка. ВКБ -приближения для определения зависимости решений от временной переменной.

Поскольку третий столбец матрицы A содержит лишь одшi ненулевой элемент йз1 = —и2, то, во-первых, дисперсионное уравнение (5.3) можно представить в виде u2det(A) = 0, где A - квадратная матрица размерности 3:

п ² — и ² + а ² (т ² - 3аФ ² + 8тг5 ф )   — 8тга ² 3 ;

A _ 8га ² 8 ф                           п ² - и ² — а ² ( т ² — 3фф ² I 8г8 8 )

— 3а ² [Ф(т ² — аФ ² ) — 8гР ^ф ]        — 3а ² [ф( т ² — фф ² ) — 8гР^

(5.4)

с 4 ф³

; ф

' 2

⁶ г 2 е⁸р V¹ + Ф\

с - Ф 3 ф |

п

‘ 2

6г ² е £ ^1 + ф ² (3+5)

п

п

и

. (5.5)

Во-вторых, из уравнения (5.4) сразу найдем тривиальное решение

(5.6)

и(3)    0.

Этому решению согласно (5.1) и (5.2) в пулевом приближении ВКБ соответствует произвольная функция А(ц)

(5.6) ■ v A G R; М = 5ф = Р = 0.                             (5.7)

Такая же нулевая мода, появляется и в теории гравитационной неустойчивости Лифшица. [23], [21], если эту теорию переформулировать в терминах ВКБ. Как показано в [23], эта. мода, исключается допустимыми преобразованиями координат. В дальнейшем мы будем опускать пулевую моду.

Дисперсионное уравнение для остальных мод возмущений (^ФДп), 5ффп) и ф(п)) относитель-ио и2 имеет вид det(A) = 0,                                           (5.8)

где п2

и2

+ 711

713 п

—

A =

—

п2

U2 + 722

723п2

733п2

и2

и введены обозначения:

711 = +й2(т2

3оФ2

+ 8^5ф);

722 =

-

й2(т2

3ф^2 + 8^S<);

712 =

8 ^й ² ^ ; ;

713 =

е) Ф3 ф2

6^2£р ^1 + ф

)

;

731 = -3й2[Ф(т2

оФ2)

8^Р ^ф ];

732 = -3й2[Мт2

ф^²) - 8 ^P ^v ];

(5.9)

_ ¹ । ^рр

⁷³³ = з ⁺ Ip ^;

721 = 8тгй ²5' Ф ;       (5.10)

e)V^2

723 =--/        .

6тт ² е Р ^/1 + ф2

—

Вычисляя определитель матрицы A (5.9) и вводя переменную ж =    - 1,                                          (5.11)

п2

получим дисперсионное уравнение для остальных мод колебаний в форме полинома по четным степеням п:

Det( A ) = (ж - 1)2(7зз - ж)п⁶ + (711 + 722)(ж - 1)(7зз - ж)п⁴ + [-(711722 - 712721)(ж - 733) +713731 + 7 23 7 32 ] п ² - 711723732 + 713721732 + 712723731 - 713722731 = 0. (5.12)

В общем случае решение дисперсионного уравнения (5.12) относительно и2 для остальных мод возмущений (МДп), 5ффп) и ф(п)) конечно, формально можно найти с помощью формулы Кардана, по результат этот будет чрезвычайно громоздким и не пригодным для исследования.

• Е.2.    ВКБ-решение дисперсионного уравнения

Будем полагать в дальнейшем справедливыми следующие порядки величии в приближении ВКБ, учитывая возможность распространения результатов па. достаточно большие времена:

п² > ^е4а); п² >й²{т²ф,оф³, m²^M^³},    Й²{т², m²} » е^ .            (5.13)

Таким образом, члены левой части дисперсионного уравнения (5.12) имеют следующие порядки в рамках ВКБ-приближения по убывающим степеням п: [n ⁶, п ⁴ й ² т²Ф, п ²й⁴т⁴Ф², п ⁰й⁴т⁴Ф²].

Поэтому вследствие (5.13) в ВКБ-приближеиии мы должны отбросить член дисперсионного уравнения с нулевой степенью п. Кроме того, мы должны отбросить и второй член в квадратных скобках (5.12), так как он мал по сравнению с коэффициентом при п4. В результате дисперсион ное м2:

уравнение (5.12) сводится к произведению линейного и квадратного уравнений относительно

(7зз — ж)[(ж - 1)2п4 + (Ун + 722)(ж - 1)п2 + (711722 - 712721)] = 0 ^ 733 - ж = 0;

(ж - 1)2п4 + (711 + 722)(ж - 1)п2 + (71172 2 — 712 721) = 0 ^ ж2п4 - Тж + Г = 0,      (5.14)

где введены обозначения:

Г = п⁴ - п²(711 + 72 2) + 711722 - 712 721,                           (5.15)

Y = 2п2 - (711 + 722).                           (5.16)

Теперь все коэффициенты дисперсионного уравнения имеют одинаковый порядок в рамках

ВКБ - приближения (5.13).

Таким образом, имеем решение дисперсионного уравнения в ВКБ - приближении: м2о) = 0;     м21) = п27зз = п2 (3 +   };

м22±) = 2 (Т ± ^ ' - 4Г) = п2

2(711 + 722) ± 2 V(711 + 722)2 + 4712721.

Таким образом, i^) ф 0, этим значениям соответствуют два значения эйконала:

д=±п vT+I •

(5-17)

(5.18)

(5.19)

соответствующие запаздывающей и опережающим волнам. Далее и22±) согласно теореме Виета для квадратного уравнения (5.14):

м22+) • м(2-) = П2Г;     м22+) + м(2-) = n2Y.                        (5-20)

• - при Г > 0 ^{м 2} ₂ +) ^{м 2} _{2 -} ) > 0 - квадраты эйконала имеют либо одинаковый знак, либо комплексно сопряженные; при Г < 0 ^м2₂+)^м2_2-) < 0 ^ квадраты эйконала имеют противоположные знаки, либо противоположные по знаку вещественные части и одинаковые мнимые. Вторая возможность, как это видно из решения (5.18), отпадает. Поэтому при Г < 0 решения (5.18) действительны и имеют противоположные знаки, положительным решениям в этом случае соответствует пара, действительны значений и±>+) - действительные, отрицательным - пара мнимых значений и±,—).

• 2.    При одновременном выполнении условий

  Г > 0, Y < 0 О п⁴ - n²(7ii + 722) + 711722 - 712721 > 0, 2п² - (711 + 722) < 0       (5.24)

Проведя несложный анализ, придем к следующему выводу.

Утверждение 1. При выполнении условий ВКБ (5.13) дисперсионное уравнение (5.3) имеет сле-дуюгцие решения:

(5.21)

(5.22)

решения и±,±) - действительные или комплексно сопряженные;

решения и±,±) - мнимые;

• 3.    При выполнении условия

  Г < 0 О п⁴ - n²(7_U + 72 2) + 71172 2 — 712 721 < 0                      (5.2 5)

решение и±>₊) - действительные, а и±>_) ^_ мнимые.

• Е.З.    Первый и второй порядки

Зависимости амплитуд найденных мод от временной переменной определяются решениями дифференциальных уравнений первого порядка, по ВКБ-приближепию. В первом порядке ВКБ имеем из (4.24) - (4.27) следующую систему обыкновенных дифференциальных уравнений первого порядка:

2ибФ ‘	- и'бФ + 2-и5Ф - 1Ф'и(А - /) — 0; а       2	(5.26)
2ибр'	а’ _       1 - и’бр + 2—ибр - -р'и(А - /) — 0; а       2	(5-27)
	а 2иА' - и’А + 2—иА — 0;	(5.28)
2и/' -	. а’ - и'/ + 2—и/ + ЗибФФ' - Зибрр — 0. а	(5.29)

Заметим, во-первых, что решение дисперсионного уравнения и±.) = 0 обращает в тождества эти уравнения, во-вторых, что уравнение (5.28) легко интегрируется, поскольку содержит полный дифференциал:

(5.30)

и а А — О1.

Вследствие указанного обстоятельства, в ряде случаев необходимо удержать члены второго порядка, по параметру ВКБ. Таким образом, получим уравнения:

′ бФ ‘‘ + 2 -бФ ‘	- |ф ' д ' —	0;	(5.31)
бр'' + 2 а бр' а	- |р,д'—	0;	(5.32)
А''	а —. + 2 А' —	0;	(5.33)
Д'' + 2-Д' + 3Ф'бФ' а	- Зр'бр' —	0.	(5.34)

В эти уравнения не входит функция эйконала, поэтому мы сразу можем получить в случае и — 0 вместо (5.30) решение:

C

А—    .                                            (5.35)

а2

Поскольку при и — 0 мы получили явное решение для А (5.30), мы можем упростить систему уравнений (5.26) - (5.29), вычитая уравнение (5.29) из уравнения (5.28) и возвращаясь затем к

2ибФ' — и'бФ + 2 -ибФ — -Ф'иф = 0; 2 (5.36) 2ибф' — и' бф + 2—ибф а — 2ф'иф = 0; (5.37) а 2ир — и'ф+ 2—иф — ЗибФФ' а + Зибфф = 0. (5.38) переменной ф = А — v.

Заметим, что уравнения (5.36) - (5.38) можно записать в следующей более компактной форме:

d абФ dq л/й

аФ'

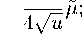
d абф аф' _ dq v = 4?и^ф;

d аф dq л/й

— -3^ (Ф'бФ' 2?^

— ф'бф').

(5.39)

Дальнейшее упрощение уравнении (5.39) на амплитуды возмущении ф = А — i ие представля ется возможным, аналитическое их исследование вследствие, во-первых, отсутствия в них малых или больших параметров и, во-вторых, отсутствия аналитических фоновых решений для функций a(q), Ф(q),ф(q) также безрезультативно. Эти слабо меняющиеся со временем функции возможно найти лишь численными методами. Но, в принципе, это и не особенно нужно, так как основную информацию о поведении возмущений ф(q, z), бФ(q, z), 6ip(q, z) несут шесть функций эйконала и±1),и+!±). Заметим лишь, что в случае постоянных значений невозмущенных потенциалов скалярных полей Ф, ф уравнения (5.39) легко интегрируются:

С2 7й      С3 7й     С4 7й

(5.40)

^бф= -----; ^бф = -----; ф=-----, ^(ф = ^фо, ф = фо).

а             а            а

F. Анализ ВКБ-решений

Вследствие линейности возмущений окончательные выражения для возмущений согласно формуле (4.7) и найденным значениям функций эйконала. (5.21) - (5.22) можно записать в форме:

/ = e*" L^V¹ '   ' + «"“ ^Д L^V¹ "⁵^±^(,>‘^,,        (⁶¹>

±             ±± где фф) и /(±)±(q) - медленно меняющиеся амплитуды возмущений q(q,z) бФ(q, z), 6y(q,z) , соответствующие перечисленным выше модам колебаний м^ун^). Поскольку согласно (4.17) и (4.20) вр > 0 Рр > 0, то и±1) - действительные функции, поэтому они соответствуют запаздывающим и опережающим волнам со слабо меняющейся амплитудой. Таким образом, согласно утверждению 1 неустойчивые моды могут соответствовать лишь функциям эйконала M±2)±(q) в области их комплексных значений. Пусть и±|)±М = ш(п, q) ± ^(n-q)     (^(п, q^^, q) е ir) ,

(6.2)

тогда, этим значениям функции эйконала, соответствуют затухающие и растущие моды колебаний с амплитудами:

р- (q)e^-4 ■^(n,’)^)d’)

p⁺(q)_e^{+ 4} ■ ¹ ",")Р

(6.3)

Растущая мода колебаний /+ соответствует неустойчивости однородного невозмущенного состояния космологической модели.

Таким образом, согласно утверждению 1 и формулам (5.10) исследуемая космологическая система, неустойчива, в следующих областях:

01 (n, q) :                n⁴ — n²(qii + 722) + 711722 — 712721 < 0;                       (G.4)

O2(n,q):  n4 — n2(7n + 722)+ 711722 — 712721 > 0,  2n2 — (711 + 722) < 0.         (G.5)

Исследуем знаки функций ГиТ, определяя знаки решений уравнения Г(п2) = 0 относительно п2 с помощью теоремы Виета. Поступая таким образом, найдем области неустойчивости:

П1(п, т): {(711 - 722)2 + 4712721 > 0,711722 - 712721 > 0,711 + 722 > 0}; п- < п2 < п+;   (6.6)

{(711 - 722)2 + 4712721 > 0,

^2(п,Т])

711722 — 712721 > 0,711 + 722 > 0},  п2 < 2(711 + 722);

(6.7)

где

{(711 - 722)2 + 4712721 < 0,

, 711 + 722 > 0},

{п2 < п-} U {п2 > п+}.

п

2    1

±   2

711 + 722 ± V (711

- 722)2 + 4712722.

(6.8)

К найденным условиям неустойчивости певозмущеппого состояния необходимо добавить условия ВКБ-приближения (4.6), ограничивающие волновое число п снизу п2 ^ 1; пту ^ 1; п4 ^ а2{т2Ф,оФ3, m2+,3+3}.                     (6-9)

F.2. Предельные случаи

F.2.1 Случай вакуумных скалярных полей

Этот случай соответствует пределу ф2 ^ 0,ф^ ^ 0. Согласно асимптотическим формулам (4.21) в этом случае р5

^ 0; S| ^ 0; S7 ^ 0; S £ ^ 0; S'; ^ 0; Р ^ф ^ 0; Р^- ^ 0; е^ф ^ 0; " ^ 0. ^-                  -

Таким образом, согласно (5.10) получим для случая вакуумного скалярного дублета:

711 — +a2(m2 - 3оФ2);   722 — -a2(m2 - 33+2); 733 — |;

712 — 0;          713 — 0;          721 — 0;

731 - -3а2Ф(т2 - оФ2); 732 - -3a2+(m2 - 3+2); 723 — 0.

Согласно (5.21) и (5.22) получим решения дисперсионного уравнения для случая вакуумного дублета:

м(0) =0; ма) = ±^; (^z ^0, ^с ^0)                       (СЛ0)

м±,+) = ±^п² - a²(m² - m² - 3оФ² + 33+²).                       (6.11)

В частности, в жестком ВКБ - приближении п2 ^ a2{m2, m2} мы получим отсюда и±2+) — ±п, т.е., получим результаты работы [22], в котором как раз и рассматривалось жесткое ВКБ - приближение для вакуумного классического поля Хиггса. На более поздних временах космологическая модель, основанная па. вакуумном скалярном дублете, неустойчива, в области:

1/т2 ^ п2 < a2(m2 - m2 - 3оФ2 + 33+2).

(6.12)

В частности, в случае стационарного (инфляционного) особого решения [16]

оФ2 = m2;    3+2 = m2

получим из (6.12)

1/ту² ^ п²< 2а2(— m2 + m2),                               (6.13)

откуда, видно, что неустойчивость стационарного особого решения в космологической модели, основанной на. вакуумном асимметричном скалярном дублете может возникнуть на. поздних временах am ^ 1 лишь при условии m2 > m2,                                         (6.14)

т.е., лишь при наличии фантомного поля и превышении массы фантомных бозонов массы классических бозонов.

Заметим, что поскольку при выполнении условия (6.13) соответствующая мода колебаний в формуле (6.1) имеет чисто мнимую функцию эйконала и(^), то в данном случае при развитии неустойчивости возмущения имеют вид стоячих растущих со временем воли, т.е., в момент возникновения неустойчивости фазовая скорость волны обращается в пуль.

F.2.2 Случай фермионов с нулевыми скалярными зарядами

Этот случай соответствует пределу и- ^ то, ф ^ ^ то. Согласно асимптотическим формулам (4.22) в этом случае все коэффициенты в формулах (4.22), включая Рр/Ер, стремятся к нулю. В результате, мы получаем для функций эйконала, формулы предыдущего случая (6.10) - (6.11). этот, казалось, бы странный результат, имеет простое объяснение. Действительно, согласно формулам (3.27), (3.28) и (4.16) возмущения фермионной компоненты в этом случае стремятся к нулю 5е_р ^ 0, 5р_р ^ 0, поэтому с точки зрения теории возмущений мы получаем формально одинаковые результаты. Разница заключается, однако в том, что невозмущенные фоновые величины a(t), Ф(7) и y (t) в этих случаях определяются различными уравнениями. Действительно, в рассматриваемом случае и„ /то согласно определениям (1.16), (1-17) и (1.18) с использованием асимптотических формул (1.24), получим асимптотики для макроскопических скаляров в певозмущеппом состоянии:

-4 + -4                 е2-2           ,е2-2

Ер -      с = 3рр  °2 - Ф - 0;  °с - д^у - 0,  (фо ^ то).

(6.15)

4-2                  2-22-2

Для предыдущего же случая ф_а ^ 0, используя асимптотические формулы (1.23), получим⁶:

1                                    1 2 -5-5

Ер-3-2(к.фк + М«3); рр;-15-2 ^ + j^);

°² - ' ^е Ф^{1 - 2 ы}вп(ф); ° - ।11 ₂ ^С sgn(y), № ^ 0).                 <6.16)

3-23-2

Таким образом, фоновые функции a(t), Ф(7) и y(t), входящие в выражения (6.10) - (6.11) различны для рассмотренных выше случаев и„ ^ то и ф_а ^ 0, в последнем случае они определяются космологической моделью с вакуумным скалярным дублетом и нейтральной нерелятивистской жидкостью.

F.3. Численное моделирование областей неустойчивости

При произвольных значениях параметров модели, в отличие от рассмотренных выше предельных случаев, исследование областей неустойчивости аналитическими методами не представляется возможным. Поэтому обратимся к численным методам исследования представленной модели. При этом в данной статье мы не будем интегрировать численными методами уравнения иевозмущеипо-го состояния космологической модели (2.16) - (2.22), так как эта. задача, сама, по себе достаточно сложная, а. ее решения обнаруживают большое разнообразие типов поведения в зависимости от параметров модели и начальных условий [15]. К этой задаче мы вернемся в ближайшем будущем.

В этой статье мы ограничимся численным моделированием областей неустойчивости, т.е., областей, определяемых неравенством г^ < 0, рассматривая зиачения функций 0.(77) = exp^(т), Ф^л) и 7(77) как некоторые заданные параметры задачи iia данный момент космологического времени 77р. Такой подход позволяет определить общие закономерности вне зависимости от конкретных особенностей эволюции фоновых функций. Ниже представлены результаты численного моделирования областей неустойчивости для модели с параметрами ttz = 1; ez = 1; т = 1; а = 1; 77- = 1; е^ = 1; / = 1; 3 = 1,                (6-17)

• - при этом изменялись лишь значения фоновых величин £ = ln о, Ф, 7.

  

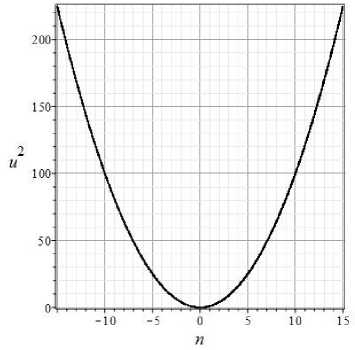
  Рис. 1. Зависимость и²(тг) (5.18) в случае классического синглета Ф = 1,7 = 0, £ = 0 (сплошная линия); £ = 1 (штриховая); £ = 1.5 (штрих - пг’иктириая): £ = 2 (пунктирная)

  
  
  

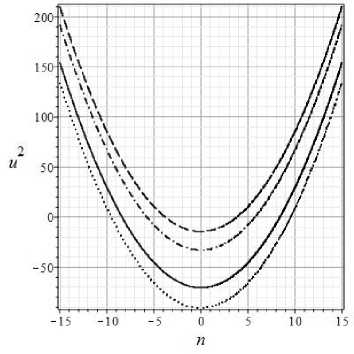
  Рис. 2. Зависимость и²(тг) (5.18) в случае фантомного синглета Ф = 0,7 = 1, £ = 0 (сплошная линия); £ = 1 (штриховая); £ = 1.5 (штрих - m’иктириая): £ = 2 (пунктирная )

  
  

На Рис. 1 и 2 показана зависимость квадрата функции эйконала и22)(тг) (5.18) от волнового числа тг для двух крайних случаев модели - классического синглета (7 = 0) и фантомного синглета (Ф = 0) при небольших значениях масштабного фактора о = 1 7 100. Из представленных графиков, во-первых, видно, так как область неустойчивости модели соответствует значениям г^ (тг) на линиях при и2 < 0, неустойчивой является модель, основанная именно на фантомном скалярном поле. Во-вторых, с увеличением масштабного фактора, границы области неустойчивости сдвигаются в область бо’льших значений волнового числа тг. При этом, однако, следует учитывать, что длина волны возмущений I = 2ттй(т7)/тг даже при постоянном тг растет благодаря масштабному фактору. График на Рис. 2 как раз соответствует случаю lc « Const, г де 1С - граничное значение длины волны неустойчивой моды, так что все колебания с I < 1с неустойчивы. Однако, достоверность этого результата, не высока, так как граничные значения волнового числа, в этом случае п ~ 5 7 10 не являются достаточно большими для обеспечения выполнения условия ВКБ -приближения п ^ 1.

На Рис. 3 показана зависимость квадрата функции эйконала и22)(п) (5.18) от волнового числа п для полного скал яркого дублета (Ф = 1,7 = 1). Из этих графиков видно, что с увеличением масштабного фактора, т.е., космологического времени, область неустойчивости расширяется в сторону бо’льших значений волнового числа п. Вместе с тем, увеличивается и инкремент нарастания амплитуды колебаний (т.е., скорости развития неустойчивости) 7 = -3(и(п)) до значений порядка 2 • 102.

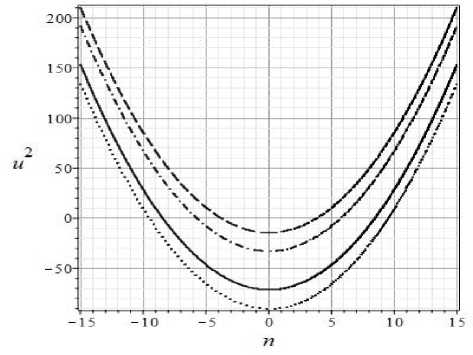
Рис. 3. Зависимость u²(n) (5.18) в случае скалярного дублета Ф = 1,/? = 1 для больших значений масштабного фактора, £ = 7 (сплошиая линия): £ = 8 (штриховая): £ = 9 (штрих -пунктирная); £ =10 а ~ 2 • 104 (пунктирная).

Заключение

Таким образом, результаты данной работы, с одной стороны, подтверждают выводы работ [12] и [13], полученные в жестком ВКБ - приближении, относительно возможности гравитационной неустойчивости системы вырожденных скалярно заряженных фермионов на. ранних стадиях эволюции Вселенной. С другой стороны, результаты исследования, во-первых, распространены па. случай скалярного дублета, а, во-вторых, снимая ограничение жесткого ВКБ - приближения, в явном виде учитывают особенности Хиггсового взаимодействия и метрические факторы. Это позволило однозначно определить области неустойчивых мод возмущений и ограничить их, как снизу, так и сверху. В свою очередь, это дает возможность определить, как время формирования, так и характерные массы объектов, возникающих в процессе развития скалярно-гравитационной неустойчивости на. ранних стадиях эволюции Вселенной. Однако, для достижения этой цели необходимо решить задачу, упоминавшуюся выше, - построить полную численную модель одновременной эволюции фоновых величин а(ту), Ф(ту) и ipQrf) и величин теории возмущений в зависимости от фундаментальных параметров взаимодействия. К этой задаче мы надеемся вернуться в ближайшем будущем.

Заметим, во-первых, что природа исследуемой нами неустойчивости космологической модели отличается от природы стандартной гравитационной неустойчивости Джинса, заключающейся в нарушении бапланса сил притяжения и давления в области достаточно больших размеров возмущений и дающей степенной рост амплитуды неустойчивых мод [23]. В пашем случае неустойчивость имеет существенно скалярно-гравитационную природу, в которой при формировании определенных условий все коротковолновые моды возмущений становятся неустойчивыми. Кроме того, амплитуда. неустойчивых мод растет по экспоненциальному закону. По-видимому, это объясняется особенностями взаимодействия фантомного скалярного поля со скалярно заряженными частицами. К этому вопросу мы намерены вернуться в будущем⁷. Во-вторых, заметим, что и в случае коротковолновых возмущений фантомное поле играет стабилизирующую роль, что можно легко увидеть из сравнения графиков на. Рис. 1 и Рис. 2, - в случае фантомного синглета, неустойчивые моды не возникают.