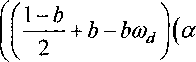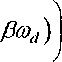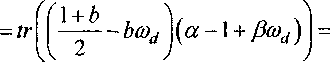Группа центральных единиц целочисленного группового кольца знакопеременной группы степени 14
Бесплатный доступ
Описывается группа центральных единиц целочисленного группового кольца знакопеременной группы степени 14. Впервые получено описание группы центральных единиц знакопеременной группы, ранг которой больше единицы.
Групповое кольцо, знакопеременная группа, центральная единица, локальная единица, неприводимые характеры
Короткий адрес: https://sciup.org/147158661
IDR: 147158661 | УДК: 517.977
Текст научной статьи Группа центральных единиц целочисленного группового кольца знакопеременной группы степени 14
Ранее группы центральных единиц целочисленных групповых колец знакопеременных групп Ап для п<1 были описаны в работе [1]. Дальнейшее продвижение уже было затруднительно получить без использования компьютера. Также в работе [2] Ферраз нашел, что ранг гп группы центральных единиц целочисленных групповых колец знакопеременных групп равен 0 тогда и только тогда, когда и g {1,2,3,4,7,8,9,12} . В работе [3] доказано, что ранг гп равен 1 тогда и только тогда, когда и g {5,6,10,11,13,16,17,21,25}. В работе [4] полностью описываются группы центральных единиц целочисленных групповых колец знакопеременных групп в случаях, когда п е {10,11,13,16,17,21,25}. В совокупности с [1] получено полное описание групп центральных единиц целочисленных групповых колец знакопеременных групп, имеющих ранг 1. В работе идет исследование самого первого случая, когда ранг > 1, а именно п = 14, в этом случае ранг группы центральных единиц целочисленного группового кольца группы Ам равен 3 .
Основные определения
Обозначение 1. Если К - ассоциативное кольцо с 1, то Un(K) = {х е К | Зх' G К хх' = х'х = 1} группа его единиц (= обратимых элементов) - мультипликативная группа кольца К .
Определение 1. Пусть К - кольцо. Центральной единицей группового кольца KG называется единица центра /(AG) этого кольца, то есть и е KG - центральная единица, если и g Z(KG) и существует такой элементы' е Z(KG), что ии' = 1.
Следующие результаты хорошо известны.
Лемма 1. Группа центральных единиц совпадает с центром группы всех единиц группового кольца. Более точно, пусть К - кольцо, тогда
Un(Z(KG)) = Z(KG) n Un(KG) = Z(Un(KG)).
Лемма 2. Имеем
G„(Z(ZG))=<-l>x7(Z(ZG)), где Z(Z(ZG)) = {v g Un(Z(ZG)) | ДУ(1С) = 1} - множество центральных единиц, у которых сумма коэффициентов при разложении по всем элементам группы равна 1.
Изучение локального случая
Пусть х ~ нецелый неприводимый характер группы АП, нецелые значения х это <\уЬ^)2 и (1-бТД)/2, где b - натуральное число, d - целое число свободное от квадратов.
Положим cod = (l + ^Jd)/2, a = (\ + bJd)l2=^-~ + ba>d и *о = (\-^Id^[2=^—^ybcod .
Следующая лемма очевидна.
Лемма 3.
Каргаполов А.В.
2 d — 1 * . * . 2 d — 1 * 1— d
®d^~®d’ tr ®d =tr rod =\, tr®d=-^- + \, todO)d= — .
Лемма 4. Пусть X - единица кольца Z^b®^, u^Z^^yjyj - локальная единица U{Z{ZAnP.
Тогда согласно [5]
у ^Х^\Х-\р
'z где z-\An |/deg %, yt - классовые суммы для классов с представителями xt, yf - целые числа.
Лемма 5. Пусть X = а + p®d, тогда
/г(Я-1) = 2(«-1) + р,(2)
trW-XP = ka-\V-^p,(3)
tr^X-Xp = . z bd +1 (tz -1) = z(2v2 - V] ^[ibd - zV)/2 + zv2 a = 1 + ztjlbd + zt)2 P = -2^2v2-vx^bd p = -zt/bd a — 1 + t 2 bd p = -—t bd Лемма доказана. Будем изучать и(2) для характеров % = /20 степени 4752, z = Z57 степени 29 952, z = Z59 степени 34 320. Лемма 7. Значения характеров ^20 > Zsi > Z59 лежат в кольцах Z[ Z/(z[®13])=<-l>x Поэтому Лю " ^ЗО 0 + ^з) » ^7 “ ^57 (^ + 8й>33) , ^59 = f59 (2 + 3(У5) , (6) где s^q, s51, s59 е {-1,1} и k,m,neZ. / х l^l 210-З5-52-72-11 13 210-З5-52-72-1 1-13 Обозначение 2. = z ( 1 =----— =----------------=------—:-------= 20 ^g^ 4?52 24•З3 -11 = 26-З2 ■ 52 • 72 ■ 13 = 9172 800, Z57 = z(z57)=JAL=^^^ 57 deg/57 29 952 28-32-13 59 deg 259 34 320 24-3-5-11-13 Лемма 8. Пусть / = exp([/(z[ /20 = 43 6 80, для z20 =26-З2■52•72■13 = 9 172 800,(7) /„=55 440, для z„ =22-33-52-72-11 = 1455 300,(8) /59 =30240, для z59 =26-34-5-72 =1270 080.(9) Доказательство. Так как z20 = 26 • З2 • 52 - 72 • 13 = 9172 800, то по лемме 3 из [1] /20 - наименьшее общее кратное чисел exp^L7^Z[ty]/P6e2)),exp(t7(z[to]/T2e3)),exp(?7(z[®]/Т2"5)), exp^TZ^Z[ Теперь по предложению 5 из [6] имеем ехр^^^/т^^З-г5 =96, ехр((7(г[®]/т2ез)) = 2-3 = 6, exp^t/^Zf®]/^2^ jj = 4-5 = 20 , exp(/7(z[®]/52e7)) = 6-7 = 42, Каргаполов А.В. Группа центральных единиц целочисленного ____________________________________группового кольца знакопеременной группы степени 14 exp^Z^]/Ее« )) = 12-13 = 156. Отсюда /20 = НОК (96, 6,20, 42,156) = 25 • 3 • 5 • 7 • 13 = 43 680 . Доказательство утверждения для /57 и /59 опустим, так как оно аналогичное. Теорема 1. Допустим, что ит^еИ^Т^Уу Тогда Я = (1+ <У] з )3360Лдля подходящего целого к . Доказательство. По лемме 7 ^гф + ^з)* = ак + Рка)п, где s е {-1,1}, к, а. Де Z. Поймём, что достаточно рассматривать случай, когда к > 0 . Заметим, что Л* = ак + ркср3 =s (1 + <д*3) = Е(Х + согзук. Тогда и(Л)и(Л*) = 1. Из алгебраической сопряжённости характеров /20 и Z21 получаем, что одновременно и(л) и и(л) принадлежат £Z(Z(Z414)). Отсюда и получаем, что достаточно рассматривать случай, когда к > 0 . Итак, к > 0 . Пусть для любого неотрицательного целого к О + ^з/ = ^+А<У13-По лемме 6 получим ак =1 + 4 939 200т(mod9172 800) и Дк =8 467 200t(mod9172 800). (10) По китайской теореме об остатках получим, что эти условия равносильны системе условий: аЛ=1 (mod 64) ак =1 (mod9) ^ак si (mod 25) Pk=Q(mod 64) Pk=^ (mod 9) ’ Pk=® (mod 25)’ ak s 1 (mod49) ak si+ 6-1 (mod 13) /?A s0 (mod 49) ’ ^=/(modl3) Согласно лемме 7 [4] имеем следующие рекуррентные соотношения: «к+2 =3ak+1+afc,a0 = 1,^=1, А+2=зд+1 + д,до=о,д=1, поскольку ?г(1 + <у13) = 3 и Normal + ®п^ = -1 по лемме 5. Посчитаем последовательности {^}”=о и {А}”=о по М°ДУЛЯМ 64,9,25,49,13. По модулю 64 имеем: {«4 }^=0 = {1,1,4,13,43,14,21,13,60,1,63,62,57,41,52,5,3,14,45,21,44,25,55,62,49,17,36, 61,27,14,5,29,28,49,47,62,41,57,20,53,51,14,29,37,12,9,39,62,33,33,4,45, 11,14,53,45,60,33,31,62,25,9,52,37,35,14,13,53,44,57,23,62,17,49,36,29,59, 14,37,61,28,17,15,62,9,25,20,21,19,14,61,5,12,41,7,62,1,1,...}, {А^о"^0’1’3’10’33’45’40’37’23’42’21’41’16’25’27’42’25’53’56’29’15’10’45’17’32’49’ 51,10,17,61,8,21,7,42,5,57,48,9,11,42,9,5,24,13,63,10,29,33,0,33,35,10,1, 13,40,5,55,42,53,9,16,57,59,42,57,21,56,61,47,10,13,49,32,17,19,10,49,29,8, 53,39,42,37,25,48,41,43,42,41,37,24,45,31,10,61,1,0,1,...}. Получаем, что эти последовательности периодичны с периодом 96, по соотношениям (И) подходят «96 д =1 (mod 64), Абд = 0 (mod 64) для любого целого р} > 0. По модулю 9 подходят а6р^ и Дрг для любого целого р2 > 0 . По модулю 25 подходят «60рз и Р№рз для любого целого р3 >0. По модулю 49 подходят Л]^ и Д12р4 для любого целого ^4>0. По модулю 13 подходят а4р5 и Д4р. для любого целого ps > 0. Таким образом, получаем к = 96/?, = 6р2 = 60/?3 = 112^>4 = 4р5. Наименьшее общее кратное чисел 96,6,60,112,4 равно 25 -3-5-7 = 3360. Применение леммы 10 завершает доказательство. Теорема 2. Допустим, что u57(X)eU^Z(ZA14)y Тогда 2. = (19 + 8®33)840тдля подходящего целого т . Теорема 3. Допустим, что u59(A)eU^Z(ZA14)y Тогда Л = (2 + Зщ5)504идля подходящего целого п. Изучение глобального случая Лемма9.Пусть u^u^X^u^X^u^X^EU^Z^ZAy^ тогда Ао = (1 + ®1з)* =ак*Ркю\з и «к-^Рк = 1 (mod 9172 800 ), А? =(19 + 8^33)'" = а'т*Дта)33 и а^+17Д =1 (mod 1455 300 ), Я59=(2 + 3®5)п = «" + р"псо5 и «"+8^" = ! (mod 1270 080). Доказательство. Докажем истинность леммы для характера j20 (для /57 и Z59 доказательство аналогичное). Рассмотрим коэффициент yv (х) соответствующий 48 -му столбцу в таблице характеров группы Л14 . Из леммы 1.45 [5]: ^И = 7” £ (degT)zWAW- (12) I I /efrr(G) В сумме (12) Д(х) = 1 для всех характеров, за исключением /2о ’ Z57 и Z59, следовательно нужно вычислить эту независящую от X часть и уже на основе данного значения искать нужную степень единицы кольца Z[®13]. Заметим также, что в столбце 48 таблицы характеров в строках, соответствующих характерам /57 и Z59 ’ стоят нули, таким образом получаем следующее выра жение для у: 1 J у ---------+ deg z?o 9172 800 0 ^зО + ^з^ , ’13 91728001 m 37 + ^3 1 / / * \ п / 2 1 (^ + 7Д-1). = —----- Щ 0-3 +69,3 + Д СУ13 +(УП =.........-................. 9172 800 v 3 3' 13 13 Н 9172 800 Из (13) следует, что для целочисленности у необходимо выполнение условия ак+1 Рк 1 (mod 9172 800 ). Лемма доказана. Найдем степени фундаментальных единиц квадратичных полей, которые необходимы для получения глобальных центральных единиц группы U (/(ZZ14)). Каргаполов А.В. Группа центральных единиц целочисленного группового кольца знакопеременной группы степени 14 Лемма 10. Пусть и = и20 (До)м57 (Д? )м59 ( Д9 ) G ^(^(^14)) > то^а ^о=(^^з)336°к ^u20gU(Z(ZZ14)), ^7=(19 + 8®33)840m и M57e[/(Z(Z44)), ^9 = (2 + Зюз)504" и u59gU(Z(Z4X4)) для подходящих k,n,m е Z . Доказательство. Докажем истинность леммы для характера ^о (ДляZsiи Z59 доказательство аналогичное). Согласно лемме 9 и китайской теореме об остатках получаем систему: ак + 7 Рк = 1 (mod 64) ак+ 7Рк -1 (m°d 9) < ак +1 Рк = 1 (mod 25) . (14) ак + 7 Рк = 1 (mod 49) ак +1 Рк = 1 (mod 13) На основании уже вычисленных при доказательстве теоремы 1 последовательностей \ак }”=0 и {А}”-0 по модулям 64,9,25,49,13 проанализируем выражение ак + 2Рк. По модулю 64 имеем: ^ак + 7 рк }”_0 = {1,8,25,19,18,9,45,16,29,39,18,29,41,24,49,43,50,1,53,32,21,31,50,53, 17,40,9,3,18,57,61,48,13,23,18,13,57,56,33,27,50,49,5,0,5,15,50, 37,33,8,57,51,18,41,13,16,61,7,18,61,9,24,17,11,50,33,21,32,53, 63,50,21,49,40,41,35,18,25,29,48,45,55,18,45,25,56,1,59,50,17, 37,0,37,47,50,5,1,8,...} . Получаем, что эти последовательности периодичны с периодом 96, по соотношениям (14) подходят индексы 0, 17 и 86. На основании леммы 10 показатель группы единиц Z20 = 43680, а так как 17, 86 не делят /20, то подходят только «96^ и Д6д для любого целого рх >0. По модулю 9 подходят а6рг и Р6р2 для любого целого р2 > 0. По модулю 25 подходят а60рз и Р60рз для любого целого р3 > 0. По модулю 49 подходят «цг^ и Д12/,4 для любого целого р4 >0. По модулю 13 подходят а4р5 и Р4рз для любого целого р5 > 0. Таким образом, получаем к-96рх = 6р2 = 60р3 =112р4 ~^р5. Наименьшее общее кратное чисел 96,6,60,112,4 равно 25-3-5-7 =3360. Лемма доказана. Следствием является теорема о строении группы центральных единиц U(Z (Z4M)). Теорема 4. UyZ Доказательство. На основании теорем 1, 2 и 3 известны локальные единицы группы U(Z(ZZX4)y Если учитывать композиции единиц квадратичных полей, порожденных различными характерами Д4, то могут появиться новые единицы группы U(Z (ZT14)), которые отсутствуют в локальном случае. В лемме 10 находится нижняя граница для степеней единиц квадратичных полей, она совпадает с локальным случаем. Следовательно, глобальный случай исчерпывается локальными единицами. Теорема доказана.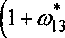
Список литературы Группа центральных единиц целочисленного группового кольца знакопеременной группы степени 14
- Алеев Р.Ж. Единицы полей характеров и центральные единицы целочисленных групповых колец конечных групп./Р.Ж. Алеев//Матем. труды. -2000. -Т. 3, № 1. -С. 3-37.
- Ferraz R.A. Simple components and central units in group rings./R.A. Ferraz//Intern. J. of Algebra. -2004. -V. 279, № l.-P. 191-203.
- Алеев Р.Ж. Ранги групп центральных единиц целочисленных групповых колец знакопеременных групп/Р.Ж. Алеев, А.В. Каргаполов, В.В. Соколов//Фундамент, и прикл. матем. -2008.-Т. 14, №7.-С. 15-21.
- Алеев Р.Ж. О группах центральных единиц целочисленных групповых колец знакопеременных групп/Р.Ж. Алеев, В.В. Соколов//Труды института математики. -2009. -Т. 15, № 2. -С. 3-11.
- Алеев Р.Ж. Центральные единицы целочисленных групповых колец конечных групп: дис.... д-ра физ.-мат. наук/Р.Ж. Алеев. -Челябинск, 2000. -355 с.
- Алеев Р.Ж. Числа Хигмана конечных групп/Р.Ж. Алеев//Матем. труды. -2000. -Т. 3, № 2. -С 3-28.