Групповые показатели риска здоровью в неоднородной когорте. Косвенная оценка по динамике событий

и должна являться предметом изучения еще до наступления этапа управления рисками.

Отметим ряд сугубо математических свойств понятия «риск», определяющих сложность процедуры оценки. Связь или потенциальная связь с факторами риска указывает на то, что мы имеем дело с условной вероятностью. Дело может усугубляться еще и тем, что при анализе специфического риска здоровью в роли одного из факторов риска обычно выделяют время или возраст, из чего можно сделать вывод, что риск здоровью – не только показатель (число), это еще и динамический случайный процесс. Наконец, если ставится задача элиминации влияния на метрологическую процедуру случайных или неконтролируемых факторов, этот риск никак не может быть оценен индивидуально, но только для однородной группы индивидуумов в качестве их некоторой общебиологической характеристики.

Типичным и широко употребляемым показателем, используемым в дескриптивной эпидемиологии профессиональных заболеваний, клинической эпидемиологии, медико-экологических и демографических исследованиях является интенсивный показатель риска1 общей или специфической смертности или заболеваемости, известный также под названиями «интенсивность риска», «сила смертно-сти/заболеваемости» (force of mortality, hazard rate), «моментный показатель риска» [4, 5]. При описании отдаленных последствий с его помощью эту величину обычно относят к году возрастной или календарной шкалы как наиболее часто употребляемой единице времени. Использование в качестве меры ряда из показателей риска обусловлено довольно неплохой воспроизводимостью его динамики при описании отдаленных последствий широкого списка эффектов, к примеру неинфекционных заболеваний, для большого количества изолированных субкогорт или субпопуляций, находящихся в сходных социально-экологических условиях. Это позволяет рассматривать интенсивный показатель во всей его динамике практически в качестве видоспецифической характеристики. Данное обстоятельство является, например, одной из причин проведения регулярного регионального скрининга всех видов онкологической заболеваемости и смертности именно по упомянутому показателю [4]. Как правило, этот показатель и есть та самая величина, избыточные значения которой на уровне 0,001‒1 ‰ в год в качестве предельно допустимых рисков2 принимаются контролирующими органами как уровни принятия решений. Интенсивный групповой показатель риска известен также под не совсем точным названием «индивидуальный риск», которое противоречит его групповой природе.

Пример 5-летнего когортного исследования

Параметр	Экспонировано	Не экспонировано
Умерло по причине	30	10
Не умерло по причине	70	90
Всего	100	100

Понятие о названном показателе и его непосредственной связи с величиной риска и другими объективными показателями нетрудно получить из опубликованного простого примера [5], воспроизведенного в таблице.

Пусть за некоторый сравнительно небольшой период времени T = 5 лет происходило наблюдение за двумя практически одинаковыми по составу группами населения (стратами), отличающимися только тем, что одна из них подвергалась, а другая не подвергалась воздействию некоторого фактора риска, влияние которого мы пытаемся оценить. Если риск ‒ это вероятность гибели по исследуемой причине, то в экспонированной группе его оценка составит очевидные 30 из 100 случаев, или R e = 0,30; аналогично в неэкспонированной R n = 10/100 = 0,10. Тогда избыточный риск смерти по изучаемой причине составит 0,3‒0,1 = 0,2; его естественно связать с действием экспозиции фактора риска. Относительный риск для действия фактора RR = R e/ R n = 3,0.

Приведенные величины – это кумулятивные смертности за рассматриваемый пятилетний период. По ним нетрудно оценить и интенсивные показатели, исходя из соотношений Me = Ne -(1 - exp (-heT)) и Mn = Nn -(1 - exp (-hnT)), а также из предположения о постоянстве интенсивных показателей в экспонированной и неэкспонированной группах. Здесь Me, Mn‒ числа «случаев» в экспонированной и неэкспонированной стратах; Ne, Nn‒ исходная заселенность страт; he, hn‒ hazards ‒ годовые показатели риска. Наличие экспонент в указанных формулах отражает тот факт, что величины he, hn являются скользящими, то есть связанными с условием дожития до текущего возраста в пределах интервала наблюдения, в то время как кумулятивные показатели Re, Rn относятся ко всему периоду наблюдения в целом по сравнению с состоянием субкогорт в начале. Благодаря этому показатели he, hn по своим математическим свойствам аналогичны непрерывной норме дисконтирования в экономической теории, порождая связь с экспоненциальными соотношениями. Расчет по ним дает he ® 71 %о в год и he, = 21 %о в год соответственно. Отношение показателей риска (hazard ratio) HR = hjhn = = 3,38 ^ RR = 3,0 под действием фактора.

Если просто не обращать внимания на двусмысленность толкования относительного риска и возвратится к названию статьи, уместно задать вопрос: в чем же проблема оценки показателей в неоднородной когорте? Ведь, судя по данным таблицы, все предельно просто. На самом же деле здесь целый ворох методологических проблем:

• 1)    показатель h = h ( t ) на самом деле не число, а функция возраста или времени, то есть процесс, в то время как в таблице оценки приведены к обычным скалярным (числовым) показателям;

• 2)    в таблице указан только один фактор, оказывающий влияние на риск, в то время как в ситуации реальной выборки или когорты почти всегда приходится иметь дело с многофакторным исследованием. Здесь нужна особая технология статистического оценивания, подразумевающая стратификацию неоднородной когорты более чем на две страты с учетом всех интересующих комбинаций факторов риска;

• 3)    как можно видеть, ни интенсивность h , ни ее кумулятивный аналог h ■ T не являются непосредственно наблюдаемыми величинами. Живучести противоположных (устаревших) воззрений способствует известное приближенное свойство величины h , позволяющее вычислять ее как «отношение числа специфических случаев к числу человеко-лет наблюдения под риском»¹. Ошибочно считать это приближенное свойство точным определением. В действительности первичной эмпирически наблюдаемой информацией является динамика отсчетов в таблице как в кумулятивной, так и в индивидуальной форме. Это обстоятельство порождает задачу косвенной оценки процесса h ( t ) или его кумулятивного аналога по наблюдениям процесса накопления отсчетов в каждой однородной страте когорты;

• 4)    отсчеты в однородной страте, являющейся частью случайной выборки, тоже случайны. В оценке же нуждается показатель некой однородной и почти генеральной совокупности. По этой причине показателям может быть дана оценка с некоторой относительной неопределенностью, которая будет тем больше, чем меньше число случаев в изучаемой когорте/страте. Например, интервальные оценки кумулятивных рисков для рассмотренных экспонированной и неэкспонированной страт (на уровне 95%-ной доверительной вероятности) составляют R e = 0,219^0,396 и R_n = 0,056^0,175, причем видно, что для неэкспонированной группы ширина интервала неопределенности превышает центральную оценку. Это обстоятельство практически запрещает нам работать с малочисленными стратами, число «случаев» в которых менее 4, так как расширенная относительная неопределенность риска заведомо

будет превышать 100 %. Менее чем по четырем точкам вообще невозможно надежно идентифицировать процесс, несмотря на то, что статистически значимые различия страт могут наблюдаться и при меньшем числе случаев [6]. Таким образом, требуется создание такого алгоритма оценивания, который сохранял бы преимущества стратификации пространства факторов вместе с возможностью идентификации оптимальной модельной зависимости показателей риска, учитывающей взаимосвязь со всеми факторами риска для всей совокупности страт одновременно.

Таким образом, актуальной и естественной является задача построения алгоритма оценки интенсивных и кумулятивных показателей специфического риска в неоднородной когорте на основе данных регистра о ее длительном наблюдении.

Описание метода оценки и его прототипа . Отметим, что интерес к проблеме неоднородности реальных наблюдений существует давно как в случае когортных выборок, так и в случае популяционных исследований медико-демографических проблем [7]. Установлено множество различных причин неоднородности, наблюдаемых при жизни представителей выборки или устанавливаемых посмертно, включая ненаблюдаемые скрытые факторы [8].

Не претендуя на всеобщий охват, в дальнейшем сосредоточим свое внимание на изучении влияния только заранее известных факторов риска, полагая латентные переменные состояния отсутствующими. Здесь остается полагаться только на интуицию врача-исследователя при ведении регистра и первичном сборе эпидемиологической информации. Это позволяет еще до начала математического анализа данных выполнить группирование индивидуумов по стратам с возможностью постоянной привязки к своей заранее определенной страте в течение всего периода наблюдения. Имплицитно предполагается, что все индивидуумы в ней имеют одинаковые шансы заболеть или умереть от любой исследуемой причины, закодированной в сборниках МКБ-9 или МКБ-10. Особенно просто это сделать в отношении факторов риска, которые можно описать в виде бинарных признаков, например пола или принадлежности к группе курящих или некурящих. Бинарным признаком может быть даже интерферирующее заболевание в анамнезе периода наблюдения. Такие факторы можно считать почти неизменными на протяжении довольно длительного времени. Некоторые количественные факторы воздействия на здоровье также могут оказаться пригодными для выбранной схемы стратификации, если характер интенсивности воздействия одинаков для всех членов когорты. Это очевидно для случаев острого однократного воздействия, либо хронического равномерного воздействия с постоянной индивидуальной интенсивностью. Тогда возможно введение такого (суррогатного) кумулятивного фактора, как доза, накопленная на конец периода наблюдения. В этом случае представляется вполне естественным анализ условной зависимости в паре «кумулятивный риск – кумулятивная доза».

Описанный подход в эпидемиологии имеет свой функциональный прототип – модуль AMFIT пакета программ Epicure3. Этот программный продукт успешно зарекомендовал себя в эпидемиологических исследованиях во всем мире [9, 10]. В частности, в области радиационно-эпидемиологических исследований он провозглашен стандартом программного обеспечения: «… Epicure is the de-facto standard for modeling radiation health effects …» [11]. На основании результатов, полученных с помощью AMFIT (алгоритм пуассоновской регрессии), базируются практически все национальные нормы радиационной безопасности в странах, имеющих радиационно опасные производства, включая Россию4. При этом считается установленным, что эквивалентная доза радиационного воздействия – общепризнанный фактор риска отдаленных радиационно-онкологических последствий.

Подход, предлагаемый в данной работе, несколько отличается от AMFIT, несмотря на то что имеет общую цель. Таких отличий три:

• а)    если придерживаться строго вероятностного метода, то описание наблюдений и построение функционала их совокупной оценки нельзя обеспечить применением пуассоновского распределения для отсчетов «случаев» в стратах, поскольку пуассоновская статистика пригодна только для описания редких событий в неограниченной выборке. Реальные когорты рано или поздно перестают быть таковыми по мере вымирания даже приближенно. Необходимо более корректное описание отклонений от основного тренда (процесса) на базе биномиальной статистики, пригодной для конечных выборок и не связанной с условием редкости событий;

• б)    во главу угла в алгоритме AMFIT положены оценки интенсивности специфических событий в ущерб оценке связанных с ними кумулятивных показателей. Между тем интенсивность не является непосредственно наблюдаемой дескриптивной характеристикой, однако вместо нее успешно может быть применен кумулятивный показатель Каплана ‒ Майера, напрямую связанный с индивидуальными отсчетами «случаев» и случайными отклонениями биномиальной природы. Применение такого показателя позволило бы повысить устойчивость оценок одновременно с сохранением возможности вычисления интенсивности событий;

• в)    в основе алгоритма AMFIT лежит метод максимального правдоподобия в формулировке Рональда Фишера, который, строго говоря, не является вероятностным, а имеет сугубо эвристическую ос-

• нову подобно своему прототипу – методу максимального правдоподобия Карла Гаусса [12].

Хотя любой алгоритм статистической обработки дает смещенные оценки, есть основания надеяться на заметное улучшение измерительной точности за счет исправления недостатков уже неплохо зарекомендовавшего себя алгоритма AMFIT, если использовать последний в качестве прототипа.

Взаимосвязь интенсивных и кумулятивных условных статистических показателей в эпидемиологии отдаленных последствий . Стремление к получению объективных оценок эпидемиологических показателей требует применения несколько более углубленного математического аппарата, чем тот, который был продемонстрирован при обработке данных, приведенных в таблице. Эта математика, однако, никого не должна вводить в заблуждение относительно намерений перейти в область аналитической эпидемиологии. Демонстрируемая методика по-прежнему соответствует обычной дескриптивной статистике, не связанной с природой причинно-следственных связей при описании состояния здоровья, если речь идет о событиях в условно однородной страте в составе неоднородной когорты. Дескриптивный подход подразумевает очевидный формализм: в тех случаях, когда потоки событий со специфической причиной смерти или заболевания в однородной группе можно описать простой марковской схемой с тремя состояниями и наличием двух конкурирующих причин выбывания из-под наблюдения, скорость изменения заселенности компартмента, отвечающего за исходное состояние, пропорциональна численности лиц, его заселяющих (рис. 1, формула (1)). Независимо от того, насколько близка такая модель к действительности, коэффициент пропорциональности между скоростью выбывания и численностью лиц в основном состоянии всегда может быть вычислен и представлен в виде суммы двух интенсивностей событий – изучаемой и конкурирующей.

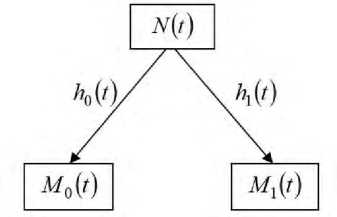
Рис. 1. Марковская структурная схема выбытия из-под наблюдения для двух конкурирующих причин смерти. Указаны компартмент исходного состояния и компартменты для двух разновидностей регистрируемых причин смерти

Схема рис. 1 может быть приближенно описана системой обыкновенных дифференциальных уравнений dN «-(hо (t)+hi (t ))•N, dM

"dT ” h i ¹ t ) ■ ^N ’

где t - время (возраст); h0 (t), h1 (t)- интенсивности событий конкурирующей и изучаемой причин смерти; N (t)- заселенность исходного состояния; M 1 (t)-кумулятивное (накопленное) число случаев смерти по изучаемой причине. Приближенность системы уравнений (1) связана с тем, что не существует производных от дискретнозначных функций, подверженных к тому же случайным флуктуациям. Однако это не мешает перейти к ожидаемым условным долям, исчисляемым от исходной численности однородной подгруппы в некоторой точке начала наблюдения t0 , а значит, к условным вероятностям или показателям распространенности в страте. Тогда соотношения станут непрерывными и точными (2):

dS = -( h о (t)+hi (t))• S, dR dt ~ hi(tS ’

если условно принять в точке начала наблюдения S ( t 0 ) = 1. В силу линейности, система (2) имеет простое аналитическое решение:

S ( t ) = S ( t\t о ) = S ( t о ) • P ( t\ t о ) • P i ( t| t о ) , (3)

• t

N R ( t\t о ) = j h i ( т ) • S ( т ) d t,           (4)

t ₀

где         P ( t i t о ) = exp (^- H о ( t i t о ) ) ;         P i ( t i t о ) =

t

= exp ( - H _i ( t| t _о ) ) ; H ( t| t _о ) = J h ( т ) d t; A R - прирост t ₀

риска смерти от изучаемой причины за период [tо, t]. По смыслу решений (3), (4) и по опыту широкого круга эпидемиологов [13–23] в этих выражениях помимо интенсивности изучаемых специфических событий ^(t) можно узнать точную функцию дожития S (t| tо), добавочный условный пожизненный риск смерти от изучаемой причины AR (t| tо), кумулятивную вероятность не умереть от изучаемой причины при условии дожития до возраста t0 и условного отсутствия конкурирующих причин смерти ‒ Pi (11 tо), а кроме того, аналог показателя Нельсона -Аалена Hi (t| tо), известного также как кумулятив- ная интенсивность специфической смертности при условии отсутствия иных причин смерти (cumulative hazard) [19, 20]. Может показаться, что связанные друг с другом показатели Pi(t| tо) и Hi (t| tо) не наблюдаемы. Однако это не так. В эпидемиологических приложениях теории мартингалов [19] установлено, что показателю Pi (t| tо) соответствует условная, но вполне измеримая функция дожития Каплана - Майера [22], а величине Hi (t| tо) - измеримый и уже упоминавшийся мартингальный показатель Нельсона ‒ Аалена. Напомним, что величина Hi (t| tо), по сути являющаяся площадью под кривой процесса h (t), успешно и эффективно более двух десятилетий контролируется в рамках онкологического мониторинга [4] в Российской Федерации. Этот показатель удобен не только для измерений в когорте, но и в популяции.

Таким образом, в рамках простой динамической схемы, приведенной на рис. 1, оказываются связанными шесть дескриптивных эпидемиологических показателей ‒ четыре кумулятивных и два интенсивных. Важно отметить, что величина показателей, являющихся относительными, привязана к разной базе. Например, условный пожизненный риск исчисляется по отношению к точке начала наблюдения, а интенсивные показатели и их кумулятивные характеристики P_i ( t| t _о ) и H _i ( t| t _о ) являются скользящими, т.е. исчисляемыми относительно достигнутой доли выживших, поскольку связаны с условием дожития до момента наблюдения. Кроме того, истинная функция дожития оказывается сильнее связанной с конкурирующими причинами смерти и неконтролируемой историей страты до начала наблюдения, по сравнению с показателями, отвечающими за изучаемую причину смерти. По этой причине показатели H _i ( t| t _о ) и P_i ( t| t _о ) представляют самостоятельный интерес. В силу связи P_i ( t| t _о ) = exp ( - H _i ( t| t _о ) ) показатель P_i ( t| t _о ) можно трактовать как некий условный аналог «функции дожития», своеобразие которого состоит в том, что его предельное значение при t ^ го может не достигать нуля, в отличие от истинной функции дожития. Такое поведение возможно, если изучаемая причина смертности не является ведущей, в отличие от совокупности конкурирующих причин смерти. Оно будет наблюдаться также и в тех случаях, когда фатальный потенциал изучаемой причины смерти конечен в силу конечности доли лиц, потенциально подверженных развитию изучаемого заболевания. Эти свойства позволяют интерпретировать показатели i - exp ( - H _i ( t| t _о ) ) и H _i ( t| t _о ) подобно величине специфического риска и численно почти отождествлять их, если только предельное значение показателя Нельсона ‒ Аалена не превышает примерно

~0,1. Этому условию практически всегда удовлетворяет популяционная кумулятивная смертность, связанная с конкретной локализацией онкологического заболевания [4]. Однако, например, смертность от всех болезней системы кровообращения в популяции обычно перекрывает это ограничение, и тогда H 1 ( t| t 0 ) не является оценкой риска. Сравнительно больших значений H 1 ( t| t 0 ) может достигать также среди контингента специализированных клиник или отделений в силу специфики отбора их пациентов. Например, в работе [24] приводятся оценки группового риска смерти от рака предстательной железы до 1 - P 1 ® 24 %, что соответствует предельному значению H 1 ® 0,27 за период более 3000 суток. Для сравнения, кумулятивный риск развития рака предстательной железы в популяции мужчин РФ за 75 лет жизни не превышает 5,7 % [4]. За показателем риска 1 - exp ( - H 1 ( t| t 0 ) ) в радиационной эпидемиологии закрепилась аббревиатура RADS [15, 16].

Принципы конструирования и параметризации модели. Байесовское интервальное статистическое оценивание. Как было показано, оценка кумулятивных показателей для отдельных страт не представляет больших технических трудностей, однако любая подробная стратификация наблюдений в пространстве факторов приводит к уменьшению числа «случаев» в каждой страте и, соответственно, к росту неопределенности оценки рисков. Поднять точность оценок и одновременно сохранить подробность описания можно только путем применения единой аппроксимирующей математической модели для всех страт одновременно. Тем самым в расчетах будут участвовать все наблюдаемые «случаи», что при соответствующей оптимизации позволит добиться большей устойчивости оценок риска. В этом состоит роль единой модели для всех страт. Она должна быть динамической, то есть пригодной для всех наблюдений, разнесенных по времени (возрасту). Строго говоря, модель должна соответствовать природе связи факторов с показателями риска, однако обычно это и является предметом исследования, то есть до завершения анализа такой модели обычно нет. В этом случае можно опереться на ожидаемое подобие динамики реализации риска во времени для различных страт h = h(t| z, в,Data), взяв за основу уже изученное поведение показателей в некоторой группе сравнения. Здесь z – вектор факторов риска; в - соответствующий вектор подгоночных параметров модели. При изучении онкологических эффектов разумно использовать популяционные показатели [4] и на основе метода возмущений ввести в описание связь с факторами риска и соответствующую параметризацию. Например, можно использовать тот факт, что большинство интенсивных показателей риска смерти от аналогичных онкозаболеваний в возрастной динамике имеет вид унимодальных функций, характеризующихся приблизительно степенным ростом в диапазоне возрастов до 60–65 лет и резким спадом в возрасте старше 75 лет.

Если непрерывная модель h (t| z, в, Data) в не- котором смысле адекватна изучаемому множеству дискретных эмпирических отсчетов Data , это будет означать попытку двойственного описания одних и тех же событий либо через отсчеты непосредственно, либо в пространстве параметров в. Естественному рассеянию в пространстве наблюдений будет соответствовать некоторое непрерывное условное распределение в пространстве параметров. Оно будет прямо представлять интерес для интервального оценивания множества подходящих параметрических гипотез, если процедуре оценки придать вероятностную форму.

Подходящим инструментом для этого является теорема Байеса, позволяющая связать два упомянутых типа условных распределений:

V (в | Data ) =

L ( Data | в ) ■ prior ( в ) | L ( Data | в ) ■ prior ( в ) d в

или v ( в | Data ) ^ L ( Data | в ) ■ prior ( в ) • (6)

Несмотря на то что байесовский подход считается прямым статистическим конкурентом известному методу максимального правдоподобия, оба подхода органически связаны друг с другом. Здесь L (Data | в)— плотность рассеяния наблюдений для фиксированной параметрической модели; V (в | Data)- плотность распределения параметров модели для собранных наблюдений; prior (в) -априорное распределение параметров предположительно адекватной модели hazard. По смыслу условных распределений ψ – правдоподобие Байеса; L – правдоподобие Фишера, а ожидаемая область наиболее вероятных параметров лежит вблизи точки максимального правдоподобия функции L, по крайней мере в тех исследованиях, результат которых до анализа опытных данных неизвестен. В данном случае соотношения (5), (6) вполне строгие, если бы не неизвестность априорного распределения prior (в), благодаря которому справедливо мнение5 о том, что понятие параметрически зависимого правдоподобия не тождественно понятию условной плотности вероятности [25]. Однако в защиту байесовского подхода отметим, что всякое новое и в особенности однократное исследование характеризуется почти полным отсутствием до-опытного знания, благодаря которому функция prior (в) заведомо характеризуется существенно большей шириной по сравнению с L (Data | в) как функцией параметров в в некоторой значимой области. Поэтому не будет большой ошибкой принять предположение о каком-либо неинформативном априорном распределении или даже о предположении prior (в )^ 1 в значимой области. Тогда формально у (в | Data) ® L (Data | в), чем фактически и пользовался Рональд Фишер, что не мешало ему в публикациях одновременно полностью отвергать байесовский подход [25]. Близость понятий байесовского и фишеровского правдоподобий оправдывает рассмотрение постоянных параметров функции правдоподобия L(Data | в) в качестве подгоночных переменных модели. То, что считается постоянным вектором в фриквентистской/частот-нической концепции Фишера и Пирсона, при более строгом рассмотрении является непрерывной случайной переменной по Лапласу / Байесу.

Отметим главное: правдоподобие для совокупности страт в силу их независимости просто равно произведению правдоподобий для каждой однородной страты. Поэтому построим правдоподобие для отдельной однородной страты. Для этого в ее пределах введем свою сетку моментов времени t i , каждый узел которой привязан к одному из специфических событий на числовой оси возраста. Точка t 0 соответствует началу наблюдения. Очень редко в одном узле может происходить до 2–3 таких событий одновременно, поэтому каждый полуоткрытый интервал ( t i _ j , t i ] между двумя соседними узлами будет связан со своим количеством накопленных специфических случаев m i . Обычно m i = 1. Общее количество накопленных случаев к рассматриваемому моменту времени t i составит M; = ^ m j .

j = 1

Совместное правдоподобие наблюдения всей последовательности специфических событий в j -й страте с вектором факторов z j , как цепи последовательных переходов, составит

ной интенсивности риска являются интегралами модельной функции интенсивности ti

H = H ( t i l t i -P z , в ) = J h ( t| z , в ) d T-     (9)

t i - 1

По своей конструкции правдоподобие (7), (8) имеет дифференциальную форму, как и традиционное правдоподобие Фишера для независимых событий, однако это не совсем так. Анализируя частные правдоподобия L i ~ п ^{Ni - 1 -} m i ( 1 - п i ) m , нетрудно заметить, что они достигают максимального значения при п o^pt = ( N i - 1 - m i )/ N i - 1 , то есть локально удовлетворяют процедуре Каплана ‒ Майера [22] на каждом i -м шаге по времени для однородной страты. Таким образом, максимизация функционала (7), (8) потенциально может привести к интерполяции кумулятивного показателя, если рассматривать оценки п i = п o^pt в качестве параметров интерполирующей модели. Разумеется, это же свойство приближенно сохранится и при меньшем числе параметров в составе рассматриваемого вектора в , но с добавлением фильтрующего свойства правдоподобия как функционала оценки. Таким образом, сконструированное правдоподобие способно одновременно обеспечить и дифференциальную, и кумулятивную аппроксимацию (регрессию) одновременно. Оценка интенсивных показателей аналогична разностному численному дифференцированию меняющейся зашумленной функции. Дифференцирование эмпирических данных ‒ плохо обусловленная (некорректная) численная операция. Напротив, производные от сглаженной кумулятивной функции будут более устойчивыми.

Технически удобнее вместо резко изменяющейся функции правдоподобия L ( Data | в) или плотности у ( в Data ) оперировать их удвоенным натуральным логарифмом, смещенным относительно точки предельного насыщения (интерполяции). Тогда для одной страты вместо поисков вблизи максимума выражения (7) следует анализировать функцию

где

Lj = L (Mmax, Mmax -Р-, M1 ^ , в) = i max

= 1-П p (M\M_1), i=1

□ ( в| Data ) = 2 - ^

( N - 1

m i ) ln

+ m i In

N i - i - m i

N _, п , .( в )

+

m

[ N i - 1 ( 1 - п , ( в ) ) J

p ( M/M i -J =

N !            n - m

-----------i ^---------- ( n i ) m i ! ( N i _ 1 - m i )!

mi

Здесь также введены обозначения п i = exp ( - H i )

и H i = H ( ti\ t _ 1 , z , в ) , где приращения кумулятив-

вблизи ее минимума. Вклады (10) следует просуммировать для всей совокупности непустых страт. Окончательно в этом случае можно говорить о достигнутой девиации (функционале оценки)

□_Е ( в ) = £ ^ j (P| Data ) ; П _у ( в| Data ) > 0. (11)

Согласно известным представлениям [26, 27], свойственным фишеровскому подходу, по величине уклонения Q_z ( в ) от нуля можно судить о качестве и статистической значимости выполненной аппроксимации, а по разности достигнутых оптимальных значений ‒ следует производить селекцию моделей. Если параметрическая зависимость девиации (11) близка к квадратичной по малым отклонениям от центра (т.е. у ( в | Data ) - почти нормальное многомерное распределение), случайное рассеяние Q , ( в ) вблизи минимума близко к распределению «хи-квадрат» с числом степеней свободы, равным разности между количеством группированных слагаемых в составе (11) и размерностью вектора р .

С учетом того, что на практике параметрическая зависимость правдоподобий L ( Data | в) и у (в | Data ) может оказаться весьма далекой от многомерного нормального распределения, более продуктивным будет завершение алгоритма оценки в логике последовательного продолжения байесовского подхода. Это означает переход к интервальному оцениванию, основанному на многомерных совместных распределениях (5), (6). Однако вместе с достаточной строгостью байесовский подход отличается высокой трудоемкостью и склонностью к накоплению вычислительных погрешностей, связанных с прямым подсчетом многомерных интегралов с участием плотности у (в | Data ) в пространстве параметров р . По этой причине более реалистичным на практике является метод статистических испытаний (метод Монте-Карло), позволяющий по большому множеству точечных псевдонаблюдений (~1 млн или более), подчиняющихся распределению у (в | Data ) , производить осреднение интересующих исследователя функций или параметров вместе с оценкой их маржинальных статистических характеристик. Алгоритм тоже трудоемкий, но, несмотря на это, – наиболее реалистический. Теоретическая основа для одного из способов его практической реализации – алгоритма Гиббса – хорошо известна [28]. При этом оценки центра распределения по методу максимального правдоподобия в случае унимодальной плотности у ( в | Data ) могут служить хорошим начальным приближением для построения стохастической последовательности псевдонаблюдений.

Результаты оценки показателей риска в неоднородной когорте с заранее известными свойствами. Рассмотрим искусственно созданный эпидемиологический регистр, описывающий некую «эталонную» когорту, события в которой не имеют случайной составляющей и точно подчиняются заранее известной модели. Выбор имитационных данных вместо реальных в данном случае является предпочтительным, поскольку не существует ни одного реального регистра, результат исследования рисков для которого заведомо совпадал бы с точными и заранее известными показателями. Поскольку в искусственной когорте будет происходить только детерминированная имитация стохастического поведения ее участников, следует ожидать возможности численного достижения нулевой или почти нулевой девиации (11). Иными словами, предстоит практически ответить на вопрос, обладает ли изучаемый алгоритм оценки асимптотической сходимостью. Этот вопрос можно адресовать не только к рассматриваемому алгоритму, но и к его прототипу – алгоритму AMFIT пакета программ Epicure, несмотря на то что ранее эта проверка не проводилось никогда.

В качестве примера рассмотрим радиационно-эпидемиологическое исследование. В основу положим следующие характеристики. Создадим имитационную выборку из четко ограниченных однородных страт, различающихся по дозе гамма-облучения (от нуля до 2 Зв), полу и достигнутому возрасту. Будем считать, что кумулятивная доза радиации – фактор риска, причем вся она была получена в режиме острого однократного равномерного облучения легких в возрасте 19 лет. Основными причинами изменения показателей онкологической смертности будем считать: а) условно линейный рост кумулятивного показателя интенсивности риска смерти от рака легких с ростом дозы, известной и ограниченной по величине; б) некоторое сокращение продолжительности жизни для всех облученных членов когорты; в) пол в качестве одного из факторов неоднородности, вызывающего как несовпадение фоновых показателей риска у мужчин и женщин, так и различия в радиочувствительности. Такие причинно-следственные связи хорошо известны по серии исследований реальной когорты лиц, подвергшихся атомной бомбардировке в Хиросиме и Нагасаки [29, 30]. Фрагмент диаграммы (мужчины) с грубыми оценками годовых показателей риска по типовой схеме трехфакторной «эталонной когорты» (пол, доза, возраст), представлен на рис. 2. Всего в базе данных имелось 25 тысяч индивидуальных записей (15 тысяч мужчин; 10 тысяч женщин). Общее количество случаев смерти от специфического рака при условии полного вымирания когорты – 1118 (995 случаев среди мужчин; 123 случая среди женщин). Общая продолжительность наблюдения когорты 1 031 414 человеко-лет. При условии группирования по 14 возрастным интервалам, двум половым признакам и пяти уровням доз можно получить 14·2·5 = 140 однородных страт. Оказалось, что из них только 91 страта содержала ненулевое количество случаев специфического рака. Непустые страты соответствовали 754 106 человеко-годам наблюдения.

Представляется очевидным тот факт, что при отсутствии случайных колебаний выборочных пока- зателей в «эталонной когорте» дозовый и возрастной тренды на рис. 2 видны невооруженным глазом. Одновременно количественные закономерности для фоновых показателей риска полностью соответствуют популяционным [4]. Исследователь риска обязан «видеть» всю заданную детализацию. Что же будут давать предлагаемый алгоритм и его ближайший прототип?

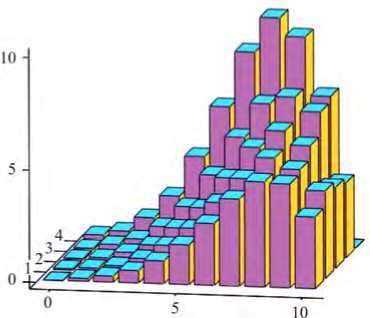
Рис. 2. Трехмерная диаграмма «возраст – доза – показатель» для мужской части «эталонной» когорты. По горизонтали отложены номера возрастных страт (14 шт.) и дозовых страт (5 шт.). По вертикали – грубые оценки показателя специфической смертности в пределах страты (‰ в год)

Оказывается, предлагаемый метод оценки процессов изменения кумулятивных и интенсивных показателей неплохо справляется с поставленной задачей, что можно видеть на рис. 3 и 4 как для субкогорты женщин, так и для субкогорты мужчин в рамках единой параметрической модели ( в ^е R 8 ) ■

Вычисленная минимальная девиация Q min для найденного экстремального решения составила в данном случае всего 0,40 единицы при существенном увеличении составляющих «наблюдений» по Каплану ‒ Майеру и росте числа степеней свободы по сравнению с ситуацией традиционной предварительной группировки с применением 5-летних возрастных интервалов (см. рис. 2). В расчете на один случай из 1118 это приблизительно соответствует визуально наблюдаемому среднеквадратическому относительному уклонению оцененных показателей hazard около ^0,40/1118 = 0,019 = 1,9 % . Остаточное уклонение ^ min не достигло точного нуля, что указывает на неустранимую роль дискретной природы записей в базе данных выборки в сравнении с непрерывной природой показателей в истинной генеральной совокупности. Однако вряд ли девиацию можно снизить еще больше. Оценка коэффициента дозового тренда избыточного кумулятивного пожизненного показателя интенсивности накопления риска и его неопределенности по информационной матрице Фишера составила 0,49 Гр ^{- 1} ( 95% ДИ: 0,24... 0,99 ) для мужчин и 0,68 Гр ^{- 1} ( 95% ДИ : 0,33...1,35 ) для женщин. Следует обратить внимание на существенную неопределенность, наблюдающуюся, несмотря на чрезвычайно малую величину достигнутой девиации. Это обстоятельство связано с преимущественной зависимостью размеров области неопределенности от кривизны функции (11) вблизи экстремума, а не от достигнутого ею минимального значения, поскольку оценка доверительных интервалов выполняется так, будто бы отсчеты в «эталонной когорте» все же подвержены случайным флуктуациям в той же мере, как если бы они были реальными. Этим биномиальная регрессия отличается от регрессии по методу наименьших квадратов.

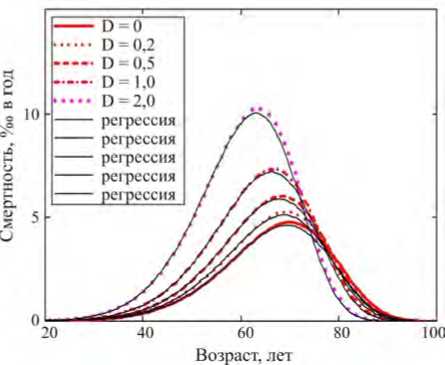
Рис. 3. Заданные и оцененные по алгоритму биномиальной регрессии динамические зависимости показателя специфической смертности среди мужчин «эталонной когорты»

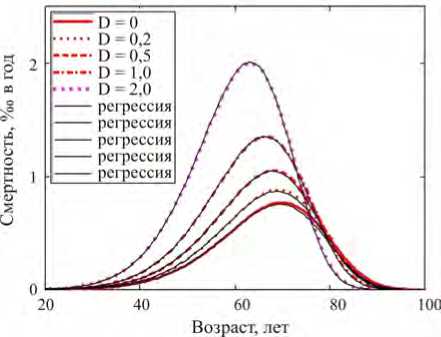
Рис. 4. Заданные и оцененные по алгоритму биномиальной регрессии динамические зависимости показателя специфической смертности среди женщин «эталонной когорты»

В отличие от полученного результата, метод AMFIT в рамках своей типовой группы моделей [9, 10, 31–33] продемонстрировал значительное систематическое смещение годовых показателей риска в области старших возрастов (рис. 5; субкогорта

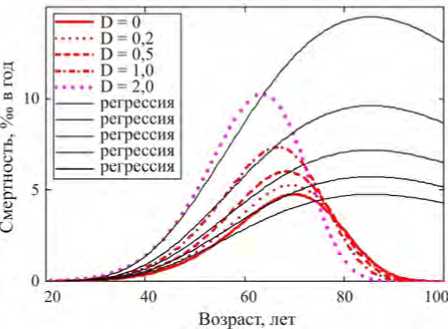
Рис. 5. Результат AMFIT-оценки дозовых и возрастных трендов показателя специфического риска в сравнении с истинным его поведением для мужской субкогорты.

На рисунке видно, что типовая модель [9, 10, 31–33] поведения фонового и исследуемого рисков является источником систематического смещения всех оценок мужчин). Неплохо аппроксимируются только восходящие участки кривых. Также модели алгоритма оказались неспособными «разглядеть» в когорте возможности взаимопересечения группы кривых hazard, связанной с некоторым сокращением продолжительности жизни облученных.

Наблюдаемая минимальная девиация (формула (11)) для найденного экстремального решения составила 24,3 единицы при числе степеней свободы 85 (число страт за вычетом числа параметров). При таком числе степеней свободы 90%-ная область ожидаемого случайного попадания минимальной девиации, казалось бы [26], распределенной по «закону хи-квадрат», должна составлять 64,7…107,5. Таким образом, наблюдаемое значение 24,3 статистически значимо меньше типичного случайного. Наблюдаемый оверфиттинг практически однозначно указывает на искусственность «эталонной когорты». Однако вызывает удивление заметное отклонение Qmin от нуля, очевидно связанное с абсурдным систематическим смещением h((| D,sex,в) в области возрастов более 75 лет и даже более 100 лет для всех дозовых воздействий. Фактически достигнутый уровень значимости p ~ 10-11 формально указывает на крайне малую вероятность уклонения модели от данных, что, однако, соответствует реальной картине только в области быстрого роста интенсивности риска (см. рис. 5), но не в широком диапазоне возрастов. Поскольку смещению подверглись все кривые показателей годового риска, то смещенными оказались и дозовые тренды. Например, годовой показатель h(r| D,sex,в) в возрасте 60 лет для мужчин смещался с темпом изменения дозы ® 82 % на 1 Зв, что почти вдвое превышает показатель дозового тренда для кумулятивной пожизненной величины, определенной предыдущим алгоритмом при тех же условиях. Несоответствие двух ти- пов относительных трендов и, следовательно, необходимость их различения отмечалась и другими авторами [34]. Таким образом, AMFIT может иметь склонность к переоценке эффектов облучения. В ряде случаев использование годовых показателей может также приводить и к недооценке реального (кумулятивного) риска [31]. Потенциальная основа для этого хорошо видна на рис. 3 и 4.

Обсуждение преимуществ и недостатков алгоритма оценки рисков в неоднородной когорте. Отметим главные обстоятельства, отличающие наш рискометрический алгоритм от своих аналогов и, прежде всего, от прототипа ‒ алгоритма AMFIT. В первую очередь, в предложенном алгоритме все отсчеты изучаемых специфических событий рассматриваются в качестве процессов биномиальной природы, а кумулятивные и интенсивные показатели определяются на вероятностной основе, а не в качестве эвристических величин. Это позволяет рассматривать оценку рисков в качестве инструментальной процедуры косвенных измерений непрерывно-распределенных оценок параметров на основе байесовского подхода. В отличие от этого, и алгоритм AMFIT, и другие, реже применяемые алгоритмы [35–38] базируются на точечной оценке всей совокупности событий и идее гладкой аппроксимации получающихся негладких эмпирических распределений в рамках частотно-дискретной статистической парадигмы Пирсона и Фишера.

Отмеченные альтернативные подходы к оценке рисков вместе с математической простотой в сравнении с оценками процессов приобретают очевидные, но игнорируемые недостатки. Например, интенсивный показатель риска в реальности не является ни константой, ни набором констант, как это предписывалось бы пуассоновской статистикой. По этой причине не ясна роль погрешности, связанной со стратификацией неоднородной когорты по возрасту. Слишком малые возрастные интервалы могут приводить к исчезновению случаев в них для когорт малого объема, при которых функционал пуассоновской регрессии может терять экстремальные свойства. Слишком большие интервалы, напротив, будут приводить к необоснованному усреднению интенсивностей накопления риска в пределах интервала. Заранее назначить оптимальную ширину интервалов при стратификации по возрасту в этом случае затруднительно. Аналогичный недостаток пуассоновской регрессии проявляется по мере вымирания когорты, когда число новых специфических случаев устремляется к нулю. На какой границе возрастного распределения следует остановиться? Более адекватен был бы биномиальный закон распределения событий, из которого закон Пуассона вытекает асимптотически как частная статистическая модель редких событий.

Отметим также, что качество аппроксимации h (^ D, sex, в) для описания радиационного воздействия зависит от того, насколько хорошо работает эта функция в случае отсутствия внешнего воздействия ( D = 0 ). Речь идет о той самой группе сравнения, на которой держится любое сравнительное исследование. Часто на этот нюанс исследователи внимания не обращают [32, 33], полагаясь на простые модели степеннóго роста или модели с насыщением. Формально это означает, что фоновый пожизненный кумулятивный показатель интенсивности может достигать очень больших значений или обращаться в бесконечность, а сам специфический риск гибели от изучаемой причины достигнет единицы. Однако на самом деле таких болезней не существует, и это видно уже на этапе предварительного группирования данных (рис. 2). Учет такой информации в моделях динамики интенсивных показателей риска уже с успехом применялся в байесовских исследованиях на ограниченных выборках с неполным периодом наблюдения и потерями данных, например, по методикам right censored spell models [39], cure rate models [40], bounded cumulative hazard models [41]. Более того, есть основания полагать, что смещение оценок на рис. 5 преимущественно связано именно с неудачной моделью фонового риска, а не только с игнорированием природы процесса и ошибкой в выборе статистического закона. Заметим, что такой показатель, как p-value, определяемый в результате применения теста отношения правдоподобий, в многомерном случае не всегда может быть надежным ориентиром при оценке качества аппроксимации.

Все сказанное не означает, что вновь предлагаемый метод оценки рисков является идеальным инструментом исследователя. Напомним, что он базируется на принципе такой стратификации когорты, которая не предусматривает переход членов когорты из страты в страту в период наблюдения. Если бы такой переход происходил, страты нельзя было бы считать независимыми единицами, а значит функционал вероятностной оценки должен строиться на иных основаниях. Уязвимым местом может быть также неполнота покрытия факторного пространства имеющимися наблюдениями, свойственная любой эмпирической выборке. Стандарты CONSORT [42] распространяются на любые выборочные исследования. Если хотя бы одна пара факторов сильно коррелирует, действие одного из факторов может быть замаскировано кажущимся действием другого. По этой причине для обеспечения успешного оценивания процессов либо когорты должны быть достаточно велики и разнообразны, либо исследование связей риска с факторами должно иметь характер контролируемого эксперимента.

Важно отметить, что данная статья не продвигает никакой теории в области аналитической эпидемиологии. В ней предлагается всего лишь инструмент практического анализа в рамках ментальной схемы «доза – время – риск» вместо традиционного ограниченного подхода «доза – риск», навязывающего толкование вреда от внешних воздействий ис- ключительно в форме простых одномерных зависимостей на плоском двухкоординатном графике. Действительно, упрощающая концепция «доза – риск» способна порождать необъяснимые артефакты в виде ложных трендов. Наглядным примером является толкование радиационно-онкологического тренда, график которого нами заимствован из документа [43].

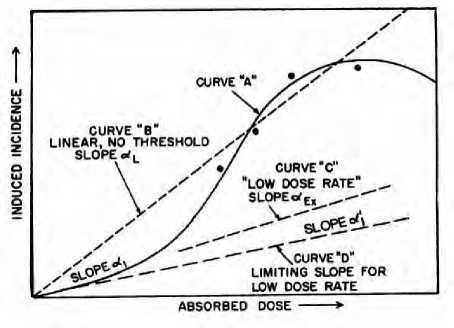
Рис. 6. Схематичное поведение избыточного показателя риска в зависимости от дозы радиационного воздействия по ожиданиям экспертов BEIR VII. Воспроизведено по отчету [43]

На нем со всей очевидностью представлен нелинейный отклик избыточной интенсивности специфических событий с явно немонотонным спадом в области больших доз. Такой тренд невозможно убедительно объяснить ни в рамках широко известной линейной беспороговой модели, ни в рамках обоснованных нелинейных моделей. Однако обратим внимание на то, что, оперируя понятием «интенсивность» вместо понятия «риск», график можно связать только с одной возрастной группой членов когорты. Тогда легко обнаружить, что в диапазоне возрастов от 60 до 65 лет на рис. 3 и 4 дозовый тренд имеет именно такой вид с характерным спадом и даже возможной сменой знака «избыточного» эффекта в еще более старших возрастных группах. При этом кумулятивный показатель риска вместе с ростом кумулятивной дозы только монотонно растет. Здесь же уместно напомнить, что известная ли-нейно-беспороговая модель «доза – эффект» Н.В. Тимофеева-Рессовского и К.Г. Циммера [44, 45] формулировалась именно для пары кумулятивных показателей, одним из которых был аналог показателя Нельсона – Аалена задолго до изобретения последнего. Близкой точки зрения на область применения кумулятивных показателей придерживался также автор широко известной концепции «эффективной дозы» [46].

Выводы. Таким образом, анализ динамики наступления специфических событий в неоднородной когорте в сочетании с байесовской методологией оценки рисков имеет определенную перспективу применения, если исследователи об- ладают детальной информацией о членах когорты в течение достаточно длительного или пожизненного наблюдения и полным исчерпывающим описанием индивидуальных факторов риска. Используемая техника вычислений лежит в рамках общепринятых эпидемиологических способов оценки вреда здоровью, комбинируя применение годовых групповых показателей риска вместе с кумулятивными. Показано, что, занимаясь прогнозированием ущерба от последствий внешнего воздействия на здоровье людей в рамках привычных ментальных схем «доза – эффект», следует отдавать предпочтение сочетанию кумулятивных доз и кумулятивных показателей риска или их дескриптивным аналогам (эффектам).

Вместе с тем нельзя не отметить повышенную трудоемкость использования описываемой параметрической версии байесовских методов. Частично преодолеть этот недостаток можно только путем создания соответствующего программного обеспе-чения6, способного автоматизировать процедуры группирования данных, выбора моделей, поиска экстремальных решений, моделирования статистической неопределенности байесовских оценок.

Финансирование . Создание методологии являлось частью исследований, финансируемых Федеральным медикобиологическим агентством (гриф «Последствия-2020»).