Hafnian of two-parameter matrices

Let A = ( a ij ) be a symmetric matrix of even order n over a commutative associative ring. The hafnian of A is defined as

Hf ( A )=      £      a i i i 2 ..■ a i n- 1 i n ,

( i 1 i 2 |...|i n- 1 i n )

where the sum ranges over all unordered partitions of the set {1, 2,..., n} into unordered pairs (i 1 i2) (in- 1 in). Therefore, if n = 4, then Hf(A) = a 12a34 + a 13a24 + a 14a23. The hafnian of the empty matrix is considered as 1. Note that the elements of the main diagonal are not included in the definition of the hafnian. For the sake of convenience, we assume that all matrices under consideration have a zero main diagonal.

A k-edge matching in a graph is a set of its k pairwise nonadjacent edges. An m-edge matching in a graph with 2m vertices is called perfect matching. If a graph is weighted, then the weight of the matching is a product of the weights of the edges included in this matching. The hafnian has a useful combinatorial property related to an important problem in graph theory and its applications: if M is the adjacency matrix of an undirected weighted graph with an even number of vertices, then Hf(M) equals the total sum of the weights of the perfect matchings in the graph. Unfortunately, the widespread use of the hafnian is limited due to the complexity of its computations in general. For example, one of the fastest exact algorithms to compute the hafnian of an arbitrary complex n x n matrix runs in O(n32n/2) time, and, as the authors show, it seems to be close to an optimal one [1].

Because the calculation of the hafnian has a high computational complexity in general, the actual problem is the discovery of efficient analytical formulas expressing the hafnian for special classes of matrices. Let T n be a symmetric (0 , 1) -matrix of order n , and let a and b be elements of a ring R . We denote a symmetric matrix of order n by T n ( a, b ) , which is obtained from T n by replacing all instances of 1 by a and all zero elements outside the main diagonal by b . For example (dots denote zeros),

( ■    1     • \                           ( ■   a   b

1 • 1    = ^ T з ( a,b ) =     a • a

• •    1     - I                               \ b    a    •

We can say that T n ( a, b ) is a two-parameter matrix, and T n is the template for T n ( a, b ) . Note that T n (1 , 0) = T n . In our work, we present a method for the exact computation of the hafnian of matrices T n ( a, b ) . In terms of graphs, we count the total sum of weights of perfect matchings in two-parameter weighted graphs (i.e., weights of the edges are only a and b ). This method is based on the formula expressing the haf-nian of a sum of two matrices through the sum of the product of the hafnians of matrices and is also closely linked to the combinatorial problem of counting the number of k -edge matchings in graphs. In theoretical physics, this problem is known as the monomer-dimer problem [2].

Recall that an arc diagram is a graph presentation method in which all the vertices are located along a line in the plane, whereas all edges are drawn as arcs (Figure 1). In this work, it will be convenient for us to represent graphs in the form of arc diagrams. Perfect matchings of arc diagrams are often called linear chord diagrams [3, 4].

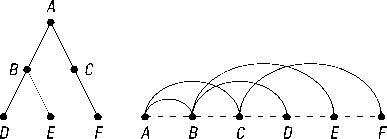
Figure 1. A binary tree and its corresponding arc diagram.

Рисунок 1. Бинарное дерево и соответствующая ему дуговая диаграмма.

• 1.    Hafnian of two-parameter matrices

To begin with, consider two properties of the hafnian. The first one is quite obvious.

Proposition 1. Let A be a symmetric matrix of even order n over a commutative associative ring R , and c G R . Then

Hf( cA ) = c ^{n/ 2} Hf( A ) .              (1)

Let Q k_,n denote the set of all unordered k -element subsets of { 1 , 2 ,..., n} . Let A be a matrix of order n and a G Q k,_n . Moreover, A [ a ] denotes the submatrix of A formed by the rows and columns of A with numbers in α , and

A{a} denotes the submatrix of A formed from A by removing the rows and columns with numbers in α .

Proposition 2. Let A and B be symmetric matrices of even order n. Then n/2

Hf( A + B ) = E E Hf( A [ a ])Hf( B{a} ) .  (2)

k =0 α ∈ Q 2 k,n

J _n ( b ) denotes a matrix of order n whose elements outside the main diagonal are equal to b . From the definition of the hafnian, it follows that

Hf( J 2 m ( b )) = b m .             (3)

m !2 ^m

Since T 2_m ( a,b ) = J 2_m ( b )+ T 2_m ( a — b, 0) , using formulas (1), (2), and (3), we can write the following:

Hf( T 2 m ( a, b )) = Hf( J 2 m ( b ) + T 2 m ( a — b, 0)) =

= £  £  Hf( J2 m (b)[ a ])Hf( T2 m (a—b, 0) {a} ) = k=0 α∈Q2k,2m

= ^£ ( a - b ) ^m-k b k kk k  £   Hf( T 2     ) .

k ⁼0                      α ^∈ Q 2 k, 2 m

Here, we use the fact that the matrix J _{2 m} ( b )[ a ] has the same form as the initial matrix J _{2 m} ( b ) , that is, J _{2 m} ( b )[ a ] is a matrix of order 2 k whose elements outside the main diagonal are equal to b .

If M is a symmetric nonnegative integer matrix, then Г( M ) denotes a multigraph with the adjacency matrix M . If a G Q _{2 k}, _{2 m} , then the hafnian Hf( T _{2 m} {a} ) equals the cardinality of a set of ( m — k ) -edge matchings in the graph Г( T _{2 m} ) ; moreover, such sets do not intersect for different a , and their union is the set of all ( m — k ) -edge matchings of the graph Г( T _{2 m} ) . Given a graph Г , let ц _к (Г) denote the number of all its k -edge matchings. By definition, we set ц о (Г) = 1 . Thus,

£   Hf( T 2 m {a} ) = ^ m-k (Г( T 2 m )) ,

α∈Q2k,2m and therefore,

Hf( T 2 m ( a,b )) =

= j m ( a — b ) ^m-k b k ⁽ kk k ^ m-k (Г( T 2 m )) . (5) k =0

Note that (5) is the special case of Theorems 1W and 3W given in [5] in terms of matching vectors of weighted graphs and their complements. The special case of (5) when a = 0 and b = 1 is also given in [6] (Theorem 4 ).

Thus, to calculate the hafnian of a two-parameter matrix by using formula (5), one needs to determine the number of k edge matchings of graphs corresponding to the matrix, which is a nontrivial task in general. One of the simplest special cases was considered in [7]. In the following section, we consider a more complicated special case.

2.    Hafnian of Toeplitz matrices Dn(a, b)

Recall that a matrix is called Toeplitz if all its diagonals parallel to the main diagonal consist of the same elements. It is obvious that a symmetric Toeplitz matrix is uniquely determined by its first row. As the template matrix T n , consider a symmetric Toeplitz matrix of order n with the first row

( 0 1 1 0 ... 0 ) .

We denote it by D _n . This matrix is the adjacency matrix of the arc diagram shown in Figure 2.

1     2    3    4         n — 2 n — 1 ⁿ

Figure 2. The arc diagram Г( D n ) .

Рисунок 2. Дуговая диаграмма Г( D _n ) .

Theorem 1. Let k and n be nonnegative integers such that k — L 1 2.I . Then, the number of k -edge matchings in the arc diagram Г( D _n ) is equal to the following:

-™"= £i( ■—-i x ^- :p )Q

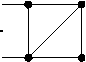
Proof. For convenience, we use the abbreviated notation w _n,_k for Ц к (Г( D _n )) . Consider a k -edge matching in Г( D _n ) . If ■ >  4 , then the following four cases are possible: the first vertex of the diagram is not incident to the edge of the matching (Figure 3(a)); the first and second vertices are connected by an edge of the matching (Figure 3(b)); the first vertex is incident to an edge of the matching, but the second vertex is not (Figure 3(c)); the first and second vertices are incident to different edges of the matching (Figure 3(d)).

(a)

(c)

(b)

1234 (d)

Figure 3. Possible cases of matchings in the arc diagram Г( D n ) .

Рисунок 3. Возможные случаи паросочетаний в дуговой диаграмме Г( D n ) .

It follows from the above that w n,k satisfies the recurrence relation

W n +4 ,k +2 =

= w n +3 ,k +2 ⁺ w n +2 ,k +1 ⁺ w n +1 ,k +1 ^{+ w} n,k ⁽⁷⁾

with the initial conditions w _n,_k = 0 for k >  [|J ; w _n, ₀ = 1 for all ■ ; w _n, 1 = 2 ■ — 3 for ■ >  2 . Consider the two-parameter generating function for the sequence w _n,k :

+ ^ L 2 J

W ( X,t ) = ^ E W n,k X ^k t ¹ . n =0 k =0

On multiplying (7) by x ^{k +3} t ^{n +3} and summing over all possible k and n , we get the following equation:

+ ^ ^L 2 ^J

W n +4 ,k +2 x ^{k +3} t ^{n +3} = n =0 k =0

+ ^ ^L n ^J

= E 2 +3 ,k +2 X ^k t ^{n +3} + n =0 k =0

+ re ^L n ^J

+ E E W n +2 ,k +1 x ^k t ^{n +3} + n =0 k =0

+ re ^L n ^J

+ E E w n +1 ,k +1 x ^{k +3} t ^{n +3} + n =0 k =0

+ re ^L n ^J

+ E £ w n,k x ^{k +3} t ^{n +3} . (8) n =0 k =0

On solving this equation, we obtain:

w ( x, t ) =

1 — t (1 + xt + xt ² + x ² t ³ )

+ re> m j i / \

=EEEEm ОС m=0 j=0 i=0 p=0 4 J 7 47

x j + p _t m + j + i + p

Fix nonnegative integers k and ■ > 2k. From (9), we see that the coefficient at xktn is equal to the sum E E (n-kk-i)(k-p)(p), over all i, p for which the inequal-ip ities i > p > 0, k — p > i, ■ — k — i > k — p hold. It can be shown that this system of inequalities is equivalent to the following system of inequalities: 0 — i — min(k, П-^_|), max(0, i + 2k — ■) — p — min(i,k — i). If we take weaker restrictions 0 — i — k, 0 — p — i on the indices i, p, then the final formula will take a more compact form, but additional zero summands may appear. This completes the proof.

Remark 1. Note that the arc diagram Г( D _n ) is isomorphic to the triangular lattice shown in Figure 4. Thus, formula (6) also allows us to calculate the number of k -edge matchings in such lattices.

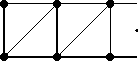
n — 3 n — 1

n — 2

(a)

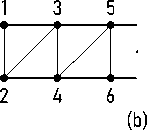
n — 2

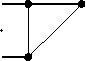
Figure 4. The triangular lattice Г( D n ) : (a) n is even; (b) n is odd. Рисунок 4. Треугольная решетка Г( D n ) : (a) n - четное; (b) n - нечетное.

Remark 2. Several initial values p k (Г( D n )) are presented in Table. The empty cells correspond to zero. Note that the sequence of the first nonzero elements in the rows is the Fibonacci sequence, the sequence of the second nonzero elements in the rows has the number A 023610 in [8], and nonzero elements of the third row coincide with the sequence A 130883 , excluding the starting element.

Number of k -edge matchings in the graph Γ( D n ) . Число k -реберных паросочетаний в графе Γ( D n ) .

k\n	0	1	2	3	4	5	6	7	8	9	10
0	1	1	1	1	1	1	1	1	1	1	1
1			1	3	5	7	9	11	13	15	17
2					2	7	16	29	46	67	92
3							3	15	43	95	179
4									5	30	104
5											8

Let R be a commutative associative ring with 1 and a,b G R . Consider a symmetric two-parameter Toeplitz matrix D 2m ( a, b ) having the first row in the form

( 0 a a b ... b ) .

On substituting the value p _m-k (Г( D 2_m )) in (5), we obtain the following theorem:

Theorem 2. If we assume that 0 0 = 1 , then the hafnian of the matrix D 2_m ( a, b ) is expressed using the following formula:

Hf( D 2 m ( a,b )) =

= jm(a - b)m-kbk ®Цт-k(Г(D2m)) , (10) z—<              k !2 k k=0

where

R m-k (Г( D 2 m )) =

m-k i

= EE( i =0 p =0

m + k

m

-

k

-

-

im

p

-

k

-

i

p    pi .

Example 1. Consider the matrix D 2_m (0 , 1) . By calculating its hafnian using formula (10) for consecutive m s, we obtain the sequence:

0 , 0 , 1 , 10 , 99 , 1146 , 15422 , 237135 , 4106680 ,...

In terms of graphs, the m -th member is equal to the number of perfect matchings in the arc diagram Г( D 2_m (0 , 1)) (Figure 5). In other words, this is the number of linear chord diagrams with m chords such that the length of every chord is at least 3 (see also [4], [9]). This sequence has the number A 190823 in [8].

123456 123456

Figure 5. The arc diagram Γ( D 6 (0 , 1)) and its only perfect matching.

Рисунок 5. Дуговая диаграмма Γ( D 6 (0 , 1)) и ее единственное совершенное паросочетание.

Conclusion

We presented a general scheme for computation of the hafnian of two-parameter matrices. We provided exact formulas for a special case of Toeplitz matrix. The resulting formulas can be used to determine the total sum of weights of perfect matchings in the graphs. In addition, we obtained new results regarding the number of k -edge matchings in some special graph. In future works, the above methods could be used to find analytical formulas for hafnians of other (two-or more) parameter matrices, or this method could be extended to multidimensional matrices, hyperhafnians, and hypergraphs.