Handling Fuzzy Image Clustering with a Modified ABC Algorithm

Published Online November 2012 in MECS

Image segmentation is a first and a critical step of image analysis. The task of image segmentation can be stated as the clustering of a digital image into multiple meaningful non-overlapping regions with homogenous characteristics according to some discontinuity or similarity features like intensity, color or texture [1,2]. Depending on the way to deal with uncertainty about the available data, the clustering process can be categorized as Hard clustering or Fuzzy clustering. A hard clustering algorithm partitions the dataset into clusters such that one object belongs to only one cluster.

This process is inappropriate for real world dataset in which there are no clear boundaries between the clusters. Since the inception of the fuzzy set theory thanks to Zadeh’ work [3], researchers incorporate the concept of fuzzy within clustering techniques to handle the data uncertainty problem. The goal of unsupervised fuzzy clustering is to assign each data point to all different clusters with some degrees of membership. The iterative unsupervised Fuzzy C-Means (FCM) algorithm is the most widely used clustering algorithm for image segmentation [4, 5, 6]. Its success is chiefly attributed to the introduction of fuzziness about the pixels’ membership to clusters in a way that postpones decision making about hard pixels’ membership to latter stages. Therefore this allows to retain much more information from the original image compared to hard clustering methods.

Despite its simplicity, FCM algorithm is sensitive to initial states and gets stuck in local optima solutions. In addition, a fuzzy clustering problem is a combinatorial optimization problem [7] that is hard to solve and obtaining optimal solutions to large problems can be quite difficult.

In order to address these issues, many fuzzy clustering algorithms based on bio-inspired methods have been introduced. The natural and intelligent behavior of biological systems, the characteristics of living organisms, their processes and behaviors evolved over thousands of years, such as self-organization, mechanisms of survival and adaptation have inspired most of the existing stochastic search heuristics. The main idea is to generate a population of candidate solutions to an optimization problem, which is iteratively optimized according to a bio-inspired dynamics in order to find better-quality solutions. Candidate solutions are selected using the fitness function, which measures their quality with respect to the optimization problem. In this field, we find Genetic Algorithms (GA) [8], Ant Colony Optimization (ACO) [9], Particle Swarm Optimization (PSO) [10],

Differential Evolution (DE) [11] and Artificial Bees Colony (ABC) algorithm [12].

Motivated by the ability of bio-inspired optimization techniques compared to analytical methods to cope with local optima by maintaining and evolving several candidate solutions simultaneously, several researchers have applied them to perform fuzzy clustering of data. Within this issue, several population based algorithms have been proposed like genetic algorithm (GA) [13, 14], Ant colony Optimization (ACO) [15,16], Particle Swarm Optimization (PSO) [17,18,19,20,21], Differential Evolution (DE) [22, 23, 24, 25, 26], Artificial Bees Colony (ABC) [27, 28] among others.

The Artificial bees colony (ABC) algorithm is a new population-based optimization algorithm developed by Karaboga in 2005 [12]. ABC algorithm is inspired from the intelligent foraging behavior of honey bees. Since its inception, it has been applied for many numerical benchmark optimization problems and has shown a high performance compared to other global optimization methods like PSO and GA, with the advantage of employing fewer control parameters [29, 30].

Despite the simplicity and the superiority of ABC algorithm, recent studies reported that it suffers from a poor exploitation process and a slow convergence rate. To overcome these pitfalls, some research papers have introduced modifications to the classical ABC algorithm in order to improve its performance and tackle more complex real-world problems [31-42].

Following this spirit, we propose in this paper, a modified ABC algorithm inspired from Differential Evolution (DE) to optimize the objective function of the FCM algorithm. We adopt the acronym MoABC-FCM (Modified ABC based FCM) to refer to the proposed algorithm. MoABC-FCM differs from the original ABC in the way to create a new solution by employed and onlooker bees. The basic search equation has been modified in a way to foster the exploitation process while preserving a balance between this process and the exploration process. Furthermore, in order to control the frequency of perturbation of the algorithm parameters, the equation that governs the generation of new solutions through iterations by employed and onlooker bees has been modified in a way similar to DE. Several benchmark images have been used to assess the performance of the proposed MoABC-FCM and a comparative study has been conducted.

The remaining of this paper is organized as follows: Section 2 presents an overview of the Fuzzy C-Means (FCM) algorithm. Artificial Bees Colony algorithm is described in Section 3. The proposed MoABC-FCM algorithm is presented in Section 4. Experimental results and comparison with FCM and other bioinspired optimization methods are summarized in Section 5. Finally, conclusions are given in Section 6.

• II.    Fuzzy C-means Algorithm

The fuzzy c-means (FCM) clustering algorithm was first developed by Dunn and later improved by Bezdek [14, 43]. This method is frequently used in pattern recognition. The algorithm is an iterative clustering process, which tends to produce an optimal c partition by minimizing the cost function defined as follows:

nc

J FCM (U, V)= ZZuikd (xk , vi )          (1)

k = 1 i = 1

where X = { x, , x₂ , x_n } is the data set in the p -dimensional vector space, n is the number of data items, c is the number of clusters with 2 <  c <  n , U_ik = U ( ^xk ) represents the membership degree of the k^th pixel to the i^th cluster, the parameter m is the degree of the fuzziness of the clustering process, v is the prototype of the center of cluster i , d ² ( x_k , v_t ) is a distance measure of similarity between the k^th data item and cluster center v .

The membership function and cluster centers are defined by (2) and (3) in the process of iterations:

1

uik =     7 x 2/( m - 1)                                 ⁽²⁾

^^ I dk 1

• j = 1 V ^djk )

and

n

Z umx.

v i = k = n ------ (3)

Z wm k=1

Starting from an initial partition chosen randomly, the FCM algorithm converges to a clustering solution by searching for local minima of the cost function. The algorithm stops when the membership function in two successive iterations does not change.

Because FCM algorithm is sensitive to the initial partition and always converges to the local optimum solution [23], a great number of stochastic search algorithms have been used to solve it. In this paper, we will use a modified version of ABC algorithm to solve fuzzy clustering problem.

• III.    The Classical ABC Algorithm

The Artificial Bee Colony (ABC) algorithm is a bioinspired optimization approach, proposed recently by Karaboga [12]. Since its introduction, the ABC algorithm has been applied to various optimization problems and has shown superior performance over other optimization methods [30].

The ABC algorithm is inspired from the intelligent foraging behavior of honey bee swarms. Its strength is its simplicity and its robustness. In the ABC algorithm, each food source position represents a solution to a specific problem and the amount of nectar in a food source represents the objective function (the fitness) of the solution. Artificial bees are classified into three classes: employed bees, onlooker bees, and scouts bees. Employed bees are affected to a particular food source (candidate solution). Every food source is explored by only one employed. Each employed bee carries with her information about the associated food source and shares the information to onlookers. Onlooker bees wait in the hive on the dance area for the information (from employed bees) about the possible food sources, and then make decision to choose a food source in order to exploit it. Onlooker bees select a food source according to a probability that is proportional to the quality of that food source. In this way, food sources with high quantity of nectar attract more onlooker bees compared to ones with a lower quantity of nectar. Scout bees are those bees that are searching randomly for a new solution in the neighborhood of the hive. The employed bee whose food source has been exhausted becomes a scout bee which explores a possible promising food source in the neighborhood of the hive. In the ABC algorithm, the number of employed or onlooker bees is generally equal to the number of solutions in the population of solutions and there is one scout.

The ABC algorithm consists of a Maximum Cycles’ Number (MCN). During each cycle, there are three main parts: sending the employed bees to the food sources and measuring their nectar quantities; selecting the food sources by the onlooker bees; determining the scout bee and exploring new possible food sources.

Firstly, the ABC algorithm generates randomly an initial population of SN solutions (food source positions) where SN represents the number candidate solutions that correspond to employed bees or onlooker bees. Each solution ( -_t , 1 <  i <  SN ) is a D dimensional vector, where D is the number of optimization parameters or decision variables. Then each nectar amount of the food source (quality of the solution) is evaluated using the fitness function associated with the optimization problem. After this initialization phase, the population of candidate solutions undergoes during each cycle, C (C = 1, 2, . . . , MCN ), search processes conducted by the employed, the onlooker and scout bees.

In the employed bees’ phase, each employed bee generates a new solution from the neighborhood of the current food source (solution). The new food source (new solution) is calculated using the following expression

• u. . = z. . + ф. . * (z. . — z, )

• i ,    j      j , j     T i , j   j , j    kj , j/

(i, j = 1,....,SN, i ^ k and j = 1,....,D)         ^

The employed bee compared its current solution with the new generated solution and memorizes the better one by means of a greedy selection mechanism.

When all employed bees have finished this search process, they diffuse the quantity of the nectar information (fitness value) and the position of the food source (solution) to the onlooker bees.

In the onlooker bees’ phase, each onlooker selects a food source with a probability proportional to the nectar amount of that food source (fitness of the solution) which is shared by employed bees. The Probability p i of selecting the food source z i is calculated using the following expression:

Pi= fz1  (i = I--SN)            (5)

Z (-)) j=1

Onlooker bee searches around its neighborhood exactly as an employed bee does using (4). It updates the selected food source position when it finds a better solution otherwise it retains the old solution.

If a food source position can not be improved through a predetermined cycles, called “ limit ”, it means that the solution has been sufficiently exploited, and it may be abandoned and removed from the population. In this case, the employed bee of that exhaustive food source becomes scout. The scout bee generates a new random food source position using the following equation:

zi,j = -min + rand (0, 1) x (z.max — z.min )

(i = 1,...., SN and j = 1,...., D)

where the z ^j and z ^j are the lower and upper bounds of the j^th component of all solutions. If the new solution is better than the abandoned one, the scout will become an employed bee.

This process is repeated until the maximum number of cycles is reached. The optimal solution is represented by the bee (solution) with the better fitness value.

A short pseudo–code of the ABC algorithm is given below [12]:

Step 1. Initialize the population of solutions

Step 2. Evaluate the population

Step 3. Cycle = 1

Step 4. Repeat

Step 5. // Employed bees phase

Step 6. Produce new solutions for the employed bees

Step 7. Apply the greedy selection process

Step 8. // Onlooker bees phase

Step 9. Calculate the probability values

Step 10. Produce the new solutions for the onlookers

Step 12. // Scout bees phase

Step 13. Determine the abandoned solution for the scout, and replace it with a new randomly produced solution

Step 14. Memorize the best solution achieved so far

There are three control parameters in the ABC algorithm: The first parameter is the number of food sources ( SN ) (solutions) which is equal to the number of employed and onlooker bees, the second one is the value of limit parameter (limit) which is equal to SN*D* 0.5 [12], and the third one is the maximum cycle number ( MCN ).

• IV.    Proposed Artificial Bees Colony Based Fuzzy Clustering

• 4.1    Modified ABC

In this section we first explain the modifications we adopted to improve the basic ABC algorithm then we described how it has been used to achieve fuzzy image clustering.

All stochastic optimization methods are based on two principles: exploitation and exploration. Exploitation is the ability to search in neighborhood of a good solution in order to find better candidate solutions if not the global optima while exploration refers to the ability to breadth search the solution space in order to find new candidate solutions. The success of any such optimization algorithm depends on an appropriate balance between exploitation and exploration processes.

From the above description of ABC algorithm, we can consider that the process of exploitation is performed by employed and onlooker bees, while scout bees are responsible for the process of exploration. According to the solution search equation of ABC algorithm described by (4), in each cycle, a new candidate solution is generated by moving the old solution towards (or away from) another solution selected randomly from the population. However, there is no guaranty that the new candidate solution is better than the previous one. Therefore, the exploitation abilities of the algorithm need to be fostered through this equation. This requires modifying this equation in a way to guide the search towards promising regions. In addition, in the classical ABC, a new solution is produced by changing only one parameter of the memorized solution, which results in a slow convergence rate as stated in [32].

In order to handle properly this pitfalls and taking inspiration from the Differential Evolution (DE) approach, we propose in this paper a modified search mechanism to improve the original ABC algorithm without altering its basic principle. DE is a populationbased stochastic method proposed by Storn and Price [11]. Since its introduction, DE has been applied successfully to solve many complex problems and exhibits a competitive performance advantage over other optimization algorithms. This approach is simple to implement and requires little parameter tuning and gives a remarkable performance. More specifically, DE exploits a population of SN potential solutions called individuals, (where SN is the population size), to effectively explore the search space. Firstly, the population is randomly initialized in the D–dimensional optimization domain by utilizing a uniform probability distribution. After this initialization step, individuals named vectors evolve over successive iterations to explore the search space and locate the optima of the objective function. At each iteration, called generation, new vectors are derived by the combination of randomly chosen vectors from the current population. This operation is called mutation, and the generated vectors are called mutant individuals. To continue, through an operation called crossover, each mutant individual is then combined with a predetermined target vector. This operation yields the so–called trial vector. Finally the selection operator is applied to decide whether target or trial population survives to the next generation by comparing their fitness function value.

The following is one of the mutation strategies used in DE algorithm [43]:

v_y ( ^G + 1) = z^ ( ^G ) + ^F * ( z , j ( ^G ) - z , , ( ^G )) + F *( z ,^ G ) - z_r  ( G ))          (7)

• 3 ,                       r ₄ , j

z ( G ), z ( G ), z ( G ) and z ( G )

where vectors r1       r2       r3           r4        are randomly chosen from the population such that r1, r2, r3 and r4 are mutually different random integer indices within {1,2,…,SN}. Further r1, r2, r3 and r4 are different. F ∈[0,  1] is a real number that controls the amplification variation of the added differential of two vectors. Larger values for F result in higher diversity in the generated population and lower values in faster convergence.

In our Modified ABC (MoABC-FCM), an approach inspired by DE, has been proposed to increase the exploitation of classical ABC. We modify the search solution described by (4) as follows v,j(G +1) = zgbest,j(G) + F*(Zi,j(G)-z,,j(G)) + F *( z, ,y( G) - z,,_(G))                 (8)

The use of the global best (gbest) solution in employed and onlooker bees’ phase can drive the new candidate solution towards the global best solution; therefore, the exploitation of ABC algorithm can be increased.

In addition, we use also in our proposed modified ABC algorithm, a modification rate MR inspired from the work of Akay and Karaboga [32] in order to control the frequency of perturbation of parameters. Employed and onlooker bees use the following equation to generate a new solution vi from a memorized solution zi:

v ,., ( G + 1) = ■

Z gbestj ( ^G ) + ^F *( Z i„ ( ^G ) - Z, , ( ^G )) +             ₍₍₎₎

F * (zr„ j (G) - zr„, (G))         if rand, < MR zi j (G)                      if rand, > MR

In (9) rand j is a uniformly distributed real random number within the range [0 1] and MR is a control parameter in the range of [0 1] which controls the number of parameters to be modified.

For each  parameter zi,j a uniformly distributed random real number (0 ≤ randj ≤ 1) is produced and if the real number is less than the modification rate (MR) the parameter zi,j is modified.

As can be observed the structure of the proposed modified algorithm is the same as the ABC; the difference lies in the way new candidate solutions are produced by employed and onlooker bees.

• 4.2 MoABC based FCM

In order to perform fuzzy clustering for image segmentation using the proposed MoABC-FCM algorithm a population of SN ( z 1 ,z 2 , z 3 ….z SN ) solutions is created where SN is the number of employed bees or onlooker bees. Each bee represents a potential solution of the fuzzy clustering problem. Each individual bee z i in generation G is formulated as following:

where C is the number of clusters and v represents the k^th cluster center for the i^th bee.

The position of each individual bee z _i of the population is initialized by randomly chosen cluster centers from the range [ g min, g max ], where g min and g max are the minimum and the maximum gray levels in the image, respectively. We have:

v i , j = g min ⁺ rand ^(0, 1) x ⁽ g max — g min ) ( i = 1,...., SN and j = 1,...., C )

The fitness of a bee indicates the degree of goodness of the solution it represents. In this work, the bee’s quality is measured using the following objective function:

fiti

1 + J, ( U , V )

and

The smaller is J , the higher is the individual fitness fit _i and the better is the clustering result.

The goal of MoABC-FCM algorithm is to determine the optimal position in the search space that satisfies (12).

When algorithm gets into convergence, we convert the optimal fuzzy partition matrix to a crisp partition matrix. The defuzzification is carried out by assigning each pixel to the cluster with the highest membership.

The MoABC-FCM algorithm is described as following:

Step 1. Initialize the cluster number c , the real number m , the size of the population SN , the value of limit, the value of MR and the maximum cycles number MCN

Step 3. Calculate the membership matrix using (2)

Step 4. Evaluate the population using (12);

Step 5. Set cycle to 1

Step 6. Repeat

Step 7. For each employed bee

Step 8. Produce new solution u i by using (9)

Step 9. Calculate the membership matrix using (2)

Step 10. Calculate the fitness using (12);

Step 11. Apply the greedy selection process

Step 12. Calculate the probability values p i for the solutions by (5)

Step 13. For each onlooker bee

Step 14. Choose a solution z i depending on p i

Step 15. Produce new solution u i by using (9)

Step 16. Calculate the membership matrix using (2)

Step 17. Calculate the fitness using (12)

Step 18. Apply the greedy selection process

Step 19. If there is abandoned solution then

Step 20. Replace that solution with a new randomly produced solution by (6) for the scout

Step 21. Assign cycle to cycle + 1

Step 22. Memorize the best solution (best cluster centers) achieved yet

Step 23. Until cycle = MCN

Step 24. Do the segmentation by assigning each pixel to the cluster for which the membership value is higher.

• V.    Computation Results and Analysis

In order to assess the performance of the proposed MoABC-FCM algorithm for fuzzy image clustering several benchmark images namely Lena, Baboon Pepper, Airplane, Hunter and cameraman have been used in our experiments. Figure 1 shows these test images. All real images are of size (512 x 512) except the Pepper image which is of size (256 x 256).

cn

j, (u , v )=££ «:r4tf - v,j||            (13)

j = 1 k = 1

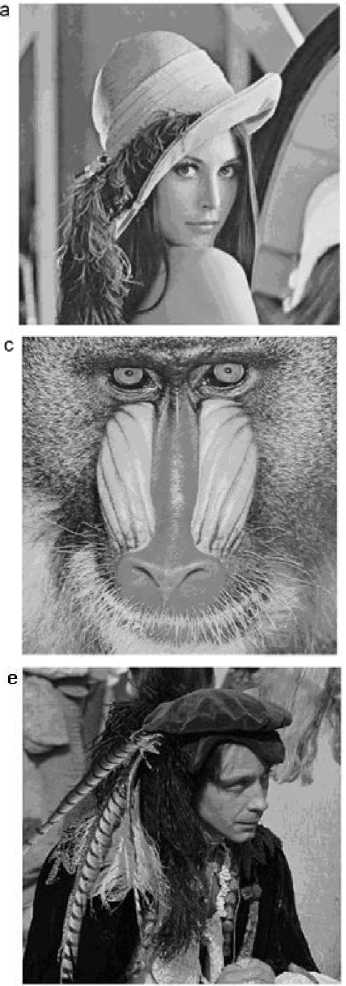
Fig.1: Real images and their histograms a)Lena; b) Pepper, c)Mandril, d) Airplane, e) Hunter, f) Cameraman

Table 1: Parameter settings for the different optimization methods

ABC-FCM		MABC-FCM		MoABC-FCM		PSO-FCM
Parameter	Value	Parameter	Value	Parameter	Value	Parameter	Value
Population size	100	Population size	100	Population size	100	Population size (SN)	50
(SN)		(SN)		(SN)		Maximum Inertia weight (wmax)	0.9
Limit	100	Limit	100	Limit	100	Minimum Inertia weight (wmin)	0.4
		MR	0.6	MR	0.6	Maximum velocity (Vmax)	+5
						Cognitive coefficient (C1)	1.429
Maximum cycle number	2000	Maximum cycle number	2000	Maximum cycle number	2000	Cognitive coefficient (C2) Maximum number of iterations	1.429 4000

We compared our MoABC-FCM algorithm with the algorithms can be found in Table 1 All algorithms are FCM algorithm [14], the classical ABC [12], MABC coded in C++ and run on a Pentium Core2duo, 3-GHz [32] and PSO [10]. Parameter settings for the different computer with 4GB RAM memory.

Table 2: Results of different optimization methods

Images	Algorithms	Xie-beni index	PC	CE
LENA C=5	FCM	0.082188	0.732009	0.485656
	PSO-FCM	0.050982	0.734573	0.483332
	ABC-FCM	0.048900	0.735051	0.483313
	MABC-FCM	0.047849	0.736357	0.471418
	MoABC-FCM	0.047311	0.736366	0.471239
Mandril C=4	FCM	0.094031	0.706386	0.589704
	PSO-FCM	0.051632	0.750942	0.537278
	ABC-FCM	0.050973	0.751026	0.531614
	MABC-FCM	0.049487	0.751139	0.438840
	MoABC-FCM	0.049433	0.752403	0.437218
Pepper C=5	FCM	0.088914	0.724946	0.489605
	PSO-FCM	0.053471	0.732658	0.485242
	ABC-FCM	0.053003	0.733062	0.482484
	MABC-FCM	0.050859	0.734328	0.481058
	MoABC-FCM	0.050342	0.734497	0.481053
Jetplane C=4	FCM	0.161078	0.723717	0.384831
	PSO-FCM	0.033943	0.746689	0.285834
	ABC-FCM	0.033711	0.747087	0.283160
	MABC-FCM	0.033153	0.756745	0.282513
	MoABC-FCM	0.033021	0.756751	0.281023
Hunter C=4	FCM	0.073205	0.718380	0.443330
	PSO-FCM	0.049453	0.764454	0.434511
	ABC-FCM	0.047490	0.764570	0.433996
	MABC-FCM	0.047457	0.766825	0.433515
	MoABC-FCM	0.047431	0.766842	0.433058
Cameraman C=4	FCM	0.051681	0.751581	0.310408
	PSO-FCM	0.038609	0.756413	0.308678
	ABC-FCM	0.038467	0.757411	0.305213
	MABC-FCM	0.038010	0.758334	0.296806
	MoABC-FCM	0.037932	0.758680	0.296419

Nc

There are several methods to evaluate measure of quality of clustering. In this paper the quality of the fuzzy clustering obtained from different algorithms is formally evaluated using the partition coefficient PC [44], classification entropy (CE) [45] and Xie-Beni validity index [46].

Partition coefficient (PC) is given by

Nc

ZZ "2

PC = 2=12= 1--- (14)

N

ZZ "y^log Uy

CE = - "' 1 i 1---------------

N

Minimum value of CE and closing value of PC to one is shows better data classified. Disadvantages of PC and CE are that they measure only the fuzzy partition and lack a direct connection to the featuring property.

Xie-Beni validity index is defined by the following equation:

Classification entropy (CE) function is given by

Vxb

cN

ZZ ",2k- < i=1 j=1

Nx minify |h- vy ||2

where x denotes the gray level of the j^{t h} pixel, v is the center of the k^th cluster; II x_i - v_k II is the Euclidean distance between the i^th pixel and the center of the k^th cluster. c stands for the number of clusters and N stands for the number of pixels.

A small value of V indicates that the clusters obtained are compacts and well separated.

For each image, twenty independent runs have been taken for each algorithm. The best results over these 20 runs for each algorithm are presented in Table 2. FCM was run for 500 iterations. Performance comparisons are made on Xie-Beni measure, CE and PC. From Table 2, we can see that the results of ABC-FCM, PSO-FCM, MABC-FCM and MoABC-FCM algorithms are better that those of FCM algorithm for all test images. However MoABC-FCM outperforms PSO-FCM, ABC-FCM and MABC-FCM which means that performance is greatly improved by the new search procedure.

• VI.    Conclusion

In this paper, we have investigated the application of a modified version of ABC algorithm to obtain better quality of fuzzy clustering result. Our modified ABC algorithm improved the exploitation process in the classical ABC algorithm. A new mutation strategy inspired from DE algorithm is introduced in employed and onlooker phase. We compared the performance of our proposed MoABC-FCM algorithm with FCM, the classical ABC, MABC and PSO on a set of real images. The experimental results showed that the MoABC-FCM is effective and efficient.

The authors would like to thank the anonymous reviewers for their careful reading of this paper and for their helpful comments.

• [1]    H. H Mohammed, Unsupervised fuzzy clustering and image segmentation using weighted neural networks”, CIAP03308-313. 2003

• [2]    N.R Pal, and S.K Pal, A review on image segmentation techniques”, Pattern Recognition 926: 1277–1294, 1993.

• [3]    L.A. Zadeh, Fuzzy sets, Inform. Control 8  338–

  353. 1965

• [4]    D.W. Kim, K.H. Lee, and D. Lee, A novel initialization scheme for the fuzzy c-means

  algorithm for color clustering, Pattern Recognition letters 25, No. 2, , pp. 227-237. January 2004

• [5]    S. Liew, Leung and W. Lau. Fuzzy Image Clustering Incorporating Spatial Continuity. In IEE Proceedings Vision, Image and Signal Processing, vol. 147, no. 2, 2000.

• [6]    Y. Marlnakls, M. Marmakl, and N. Matsatsinls, A Hybrid Discrete Artificial Bee Colony – GRASP Algorithm for Clustering. Decision Support Systems, 548-553 2009.. IEEE.

• [7]    J. G. Klir and B. Yuan, Fuzzy sets and fuzzy logic, theory and applications, Prentice-Hall Co., 2003.

• [8]    D.E. Goldberg, Genetic Algorithms in Search, Optimization, and Machine Learning..Addison-Wesley, Reading, MA 1989.

• [9]    M. Dorigo,, Stutzle,. The ant colony optimization metaheuristic:   algorithms, applications and

  advances. Technical Report IRIDIA-32 2000.

• [10]    J. Kennedy and R.C Eberhart, Particle swarm optimization. In Proc. IEEE Int. Conf. Neural Netw., Perth, Australia,. vol. 4, 1948–1972. 1995

• [11]    R. Storn, and K. Price, Differential Evolution — a simple and efficient heuristic for global optimization over continuous spaces. Technical Report TR-95-012.,ICSI. 1995

• [12]    D. Karaboga, An idea based on honey bee swarm for numerical optimization, technical Report TR06, Erciyes University, Engineering Faculty, Computer Engineering Department,. 2005

• [13]    F. Klawonn, and A. Keller. Fuzzy clustering with evolutionary algorithms. International Journal of Intelligent Systems, , 13: 975–991. 1998

• [14]    J. Bezdek, and R. Hathaway. Optimization of fuzzy clustering criteria using genetic algorithms. in: Proc. of the IEEE Conf. on Evolutionary Computation, vol. 2, , 589–594. 1994

• [15]    B. Zhao, An Ant Colony Clustering Algorithm, Sixth International Conference on Machine Learning and Cybernetics, Hong. Kong.. pp.39333938 2007.

• [16]    W. Liu, J. L. A clustering algorithm FCM-ACO for supplier base management. Lecture Notes in Computer Science including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics,. 6440 LNAIPART 1, 106-113. 2010

• [17]    A. Szabo, L.N.D. Castro, and M.R. Delgado, The proposal of a fuzzy clustering algorithm based on particle swarm. 2011 Third World Congress on Nature and Biologically Inspired Computing. IEEE.

• [18]    C. Li, J. Zhou, P. Kou, and J. Xiao, A novel chaotic particle swarm optimization based fuzzy

  clustering algorithm. Neurocomputing, 83, 98-109. 2012. Elsevier.

• [19]    E. Sivaraman, S. Arulselvi, and K. Babu, Data driven fuzzy c-means clustering based on particle swarm optimization for pH process. 2011 International Conference on Emerging Trends in Electrical and Computer Technology. IEEE 2011.

• [20]    F. Samadzadegan, and A.A. Naeini,. Fuzzy clustering of hyperspectral data based on particle swarm optimization. 2011 3rd Workshop on Hyperspectral Image and Signal Processing Evolution in Remote Sensing WHISPERS. 2011IEEE.

• [21]    T. Runkler, and C. Katz. Fuzzy clustering by particle swarm optimization. IEEE Int. Conf. on Fuzzy Systems, 601–608. 2006

• [22]    S. Das, and S. Sil, Kernel-induced fuzzy clustering of image pixels with an improved differential evolution algorithm. Information Sciences, . 1808, 1237-1256. 2010 Elsevier Inc.

• [23]    S. Das, A. Abraham, and A. Konar, Automatic Clustering Using an Improved Differential Evolution Algorithm. IEEE Transactions on Systems Man and Cybernetics Part A Systems and Humans. IEEE. 2008.

• [24]    U. Maulik, and I. Saha, Automatic Fuzzy Clustering Using Modified Differential Evolution for Image Classification. IEEE Transactions on Geoscience and Remote Sensing. 2010.

• [25]    X. Zhang, Q. Bai, Q., and X. Yun, A combinatorial Artificial Bee Colony algorithm for travelling salesman problem. IEEE 3rd International Conference on Communication Software and Networks. 2011. IEEE.

• [26]    Z. Chi, J. Yan, and T. Pham, Fuzzy algorithms with application to image processing and pattern recognition”. World Scientific, Singopore 1996.

• [27]    C. Zhang, D. Ouyang, and J. Ning, An artificial bee colony approach for clustering. Expert Systems with Applications, 377, 4761-4767. 2011 Elsevier Ltd.

• [28]    M. Taherdangkoo, M. Yazdi, and M.H. Rezvani, Segmentation of MR brain images using FCM improved by artificial bee colony ABC algorithm. Proceedings  of  the 10th IEEE International

Conference  on  Information Technology and

Applications in Biomedicine. IEEE 2010..

• [39]    L. Xiujuan, H. Xu, and Z. Aidong, Improved artificial bee colony algorithm and its application in data clustering. 2010 IEEE Fifth International Conference on BioInspired Computing Theories and Applications BICTA pp. 514-521. IEEE. 2012

• [40]    N. Baktash and M. R. Meybodi A New Hybrid Model of PSO and ABC Algorithms for Optimization in Dynamic Environment. International Journal of Computer Theory and Engineering, Vol. 4, No. 3, June 2012

• [41]    W. Gao, and S. Liu, A modified artificial bee colony algorithm. Computers & Operations Research, 393, 687-697 2012.. Elsevier.

• [42]    W. Zou, Y. Zhu, H. Chen, and X. Sui, A clustering approach using cooperative artificial bee colony algorithm, Discrete Dynamics in Nature and

  Society, vol. 2010, Article ID 459796, 16 pages, 2010.

• [43]    K, Price, R.M. Storn, and J.A. Lampinen, Differential Evolution: A Practical Approach to Global Optimization. Springer. ISBN 978-3-54020950-8. 2005

• [44]    J. C Bezdek. Cluster validity with fuzzy sets. J Cybern;3:58–73. 1974

• [45]    L.O. Hall, and P.M. Kanade, Swarm Based Fuzzy Clustering with Partition Validity. The 14th IEEE International Conference on Fuzzy Systems 2005 FUZZ 05. Ieee. 2005

• [46]    X. L. Xie and G. Beni, A validity measure for fuzzy clustering. IEEE Trans. Pattern Anal. Mach. Intell., vol. 13, no. 8, pp. 841–847, Aug. 1991.

OUADFEL Salima , received her state engineer degree, master degree in computer science from Mentouri University in Constantine Algeria and she received a PhD in Computer Science from the University of Batna, Algeria, in 2007. She is currently an Associate Professor at the computer science department of Mentouri University and a researcher at MISC laboratory Constantine City. Her current research includes natural inspired metaheuristics and their applications for image processing.

MESHOUL Souham , received the state engineer degree, master degree and State doctorate degree in computer science from Mentouri University in Constantine Algeria. She is currently an associate professor at the computer science department and a researcher at MISC laboratory Constantine City. Her current interests include computational intelligence and its applications, complex systems, bioinformatics, pattern recognition and image analysis and understanding.