Хаотическая динамика параметров треморограмм в условиях стресс-воздействий
Автор: Иляшенко Л.К., Баженова А.Е., Берестин Д.К., Григорьева С.В.
Журнал: Российский журнал биомеханики @journal-biomech
Статья в выпуске: 1 (79) т.22, 2018 года.
Бесплатный доступ
Выполнено практическое применение теории хаоса - самоорганизации в оценке стресс-реакции нервно-мышечной системы испытуемых на локальное низкотемпературное воздействие (охлаждение кисти руки). Показана низкая эффективность статистических методов расчета параметров треморограмм и высокая эффективность расчета параметров хаоса треморограмм. Практическая возможность применения метода расчета параметров фазовых пространств в двухмерном фазовом пространстве демонстрирует количественную меру реальных изменений параметров нервно-мышечной системы человека в условиях холодового воздействия. Анализ состояния биомеханической системы производился на основе сравнения площадей s фазовых плоскостей мужчин с различной физической подготовкой и метода расчета матриц парных сравнений выборок треморограмм. В конечном итоге анализ состояния биомеханической системы проводился на основе сравнения площадей фазовых плоскостей. Площади находились как произведение двух вариационных размахов фазовых координат Δ x 1 и Δ x 2, где x 1 - перемещения конечности, а х 2 - координата скорости перемещения конечности, х 2= dx 1/ dt. Уже в первом приближении площади фазовых плоскостей демонстрировали различия значений до и после локального холодового воздействия. После локального холодового воздействия на конкретных примерах происходит увеличение площадей фазовых плоскостей в 2-3 раза. При внешнем воздействии (холодовом) увеличивается доля стохастики, и у обоих испытуемых распределение площадей нормальное (в спокойном состоянии распределение ненормальное). Локальное холодовое воздействие приводит к трехкратному увеличению числа пар k совпадений выборок треморограмм у мужчин, и это не зависит от их физической подготовки. Такие охлаждения (как стресс-агенты) проявляются в рамках именно нового подхода (по параметрам площадей фазовых плоскостей).
Тремор, фазовая плоскость, холодовый стресс, матрица парных сравнений
Короткий адрес: https://sciup.org/146282085
IDR: 146282085 | УДК: 531/534: | DOI: 10.15593/RZhBiomeh/2018.1.06
Текст научной статьи Хаотическая динамика параметров треморограмм в условиях стресс-воздействий
Локальное или общее (при закаливании, например) охлаждение человека является мощным стресс-агентом, который вызывает существенную реакцию во всей нервно-мышечной системе. Существенно, что в условиях Севера РФ такие воздействия довольно частые и они обусловлены особыми климато-географическими факторами, которые оказывают негативное влияние на качество жизни и здоровья каждого жителя Югры [10, 19–21]. Низкотемпературным воздействиям характерна хаотическая динамика их изменения. Одновременно возможно также резкое изменение атмосферного давления, влажности и температуры атмосферного воздуха. Необходимо отметить, что температуры около минус 30–35°C являются характерными для зимнего периода территории Ханты-Мансийского автономного округа – Югры. Поэтому изучение низкотемпературного воздействия как стресс-агента не только имеет научное значение (для биомеханики и физиологии), но и связано с производительностью и работоспособностью населения северных регионов РФ (в нашем случае речь идет о Югре). Влияние гипотермальных воздействий на состояние нервно-мышечной системы приводит к различным негативным последствиям [22-25, 27]. Реакция же самого организма человека зависит от возрастных периодов и его физической активности, что уже отмечалось рядом авторов [1–6]. Адаптация человека в этих условиях достигается путём напряжения и сложной перестройки гомеостатических систем организма [7–12].
В связи с этим изучение реакции нервно-мышечной системы на холодовый стресс-агент является одним из важных направлений развития психофизиологии и биомеханики. При этом необходимо понимать, что традиционные статистические методы в изучении тремора или теппинга не дают объективных результатов в силу непрерывной и хаотической динамики поведения регистрируемых параметров треморограмм и теппинграмм. В рамках новых подходов, обеспечивающих регистрацию реального гомеостаза нервно-мышечной системы, общее состояние функциональных систем организма человека к гипотермальным воздействиям представляет особый интерес в рамках именно теории хаоса-самоорганизации [13–18, 26, 29]. В наших исследованиях выполнялся анализ параметров нервно-мышечной системы человека, который характеризует изменения параметров треморограмм именно у мужчин при локальном холодовом воздействии. Более того, вся теория хаоса-самоорганизации разрабатывается сейчас для индивидуальной биомеханики, медицины и физиологии. В рамках этих результатов предлагаются новые тесты по параметрам треморограмм, которые можно использовать в практической деятельности тренера или медицинского работника [1–6, 19–25] (именно на основе регистрации треморограмм).
Целью исследования является оценка особенностей хаотической динамики тремора как микродвижений верхних конечностей мужчин, которые имеют различную физическую активность.
Методы и организация исследования
Объект и методы исследования. В исследовании приняли участие мужчины, проживающие на территории Ханты-Мансийского автономного округа – Югры не менее 5 лет. Средний возраст обследуемых 28 лет. В зависимости от степени физической активности было сформировано две группы мужчин по 15 человек. В первую группу вошли испытуемые мужчины, занимающиеся физическими упражнениями нерегулярно (неспортсмены), т.е. менее трех раз в неделю. Во вторую
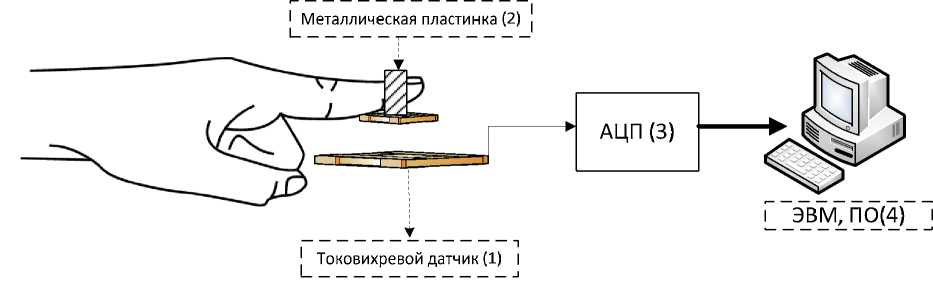
Рис. 1. Схема биоизмерительного комплекса регистрации тремора группу вошли мужчины, профессионально занимающиеся спортом (спортсмены), имеющие спортивную квалификацию не ниже первого взрослого разряда и продолжающие заниматься систематическими физическими упражнениями более трех раз в неделю.
У испытуемых регистрировались параметры тремора с помощью биофизического измерительного комплекса, разработанного в Лаборатории биокибернетики и биофизики сложных систем при Сургутском государственном университете (рис. 1) [11–14]. Установка включает металлическую пластинку 2 , которая крепится жестко к пальцу испытуемого, токовихревой датчик 1 , усилитель, аналого-цифровой преобразователь 3 и компьютер с оригинальным программным обеспечением [12–14]. В качестве фазовых координат, помимо первой координаты х 1 = х ( t ) в виде перемещения конечности, второй координатой ( x 2 ) была скорость перемещения пальца х 2 = v ( t ) = dx 1 /dt . Регистрируемые с помощью аналого-цифрового преобразователя 3 треморограммы квантовались с постоянным периодом квантования t = 0,01 с и регистрировались в виде файлов (общее время регистрации i -й выборки T = 5 с, количество точек в таком биомеханическом файле z = 500). Перед испытуемыми стояла задача удержать палец в пределах заданной области, осознанно контролируя его неподвижность. Все испытуемые проходили 15 серий эксперимента ( N = 15), в каждой из которых регистрация тремора проводилась 15 раз ( n = 15) в спокойном состоянии и аналогично ( N = 15, n = 15) после локального холодового воздействия (испытуемый погружал кисть на 2 минуты в емкость с водой температурой T ≈ 4 ○С), т.е. всего имеем 225 выборок треморограмм для каждого испытуемого [1–6, 14, 28].
Обработка данных и регистрация тремора конечности испытуемых проводилась с помощью компьютера (использовалась программа Сharts 3). Благодаря запатентованному программному продукту строились фазовые плоскости и рассчитывались их площади S в виде S = Δ x 1 ∙ Δ x 2 , где Δ x 1 – вариационный размах для треморограмм по x 1 ; Δ x 2 – вариационный размах по x 2 . Производились также попарное сравнение отрезков треморограмм для каждой выборки x 1 = x 1 ( t ) треморограмм испытуемого на предмет принадлежности всех этих выборок к общей генеральной совокупности (у одного и того же испытуемого). Делали это путем расчета матриц парных сравнений выборок x 1 .
Статистическая обработка данных осуществлялась при помощи программного пакета Statistiсa 10 . Анализ соответствия вида распределения полученных данных закону нормального распределения производился на основе вычисления критерия Шапиро-Уилка. Было установлено, что распределение Гаусса не может быть применено для всех выборок треморограмм. Далее при использовании непараметрического парного сравнения треморограмм с помощью критерия
Вилкоксона были построены 30 таблиц парных сравнений выборок треморограмм для каждого испытуемого в виде 15 серий экспериментов, в каждой из которых было по 15 сравниваемых выборок треморограмм в спокойном состоянии и после локального холодового воздействия. Одновременно для этих же выборок треморограмм рассчитывались параметры квазиаттракторов (в частности площади).
Результаты исследования
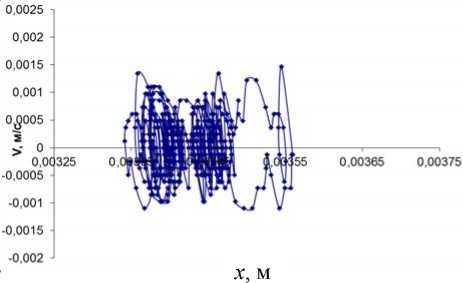
В рамках теории хаоса-самоорганизации нами были построены фазовые плоскости для всех 225 выборок, т.е. для всех 15 серий ( N ) экспериментов по 15 выборок в каждой ( n ) у каждого испытуемого до и после локального холодового воздействия. Для квазиаттракторов были рассчитаны площади S , которые находились как произведение двух вариационных размахов фазовых координат Δ x 1 и Δ x 2 , т.е. S = Δ x 1 ∙Δ x 2 , характерный пример фазовых траекторий до и после локального холодового воздействия представлен на рис. 2.
а
Рис. 2. Пример фазовых траекторий одного из экспериментов испытуемого 1: а – до локального холодового воздействия ( S до = 0,56∙10–6 у.е.);
б – после локального холодового воздействия ( S после = 1,5∙10–6 у.е.)
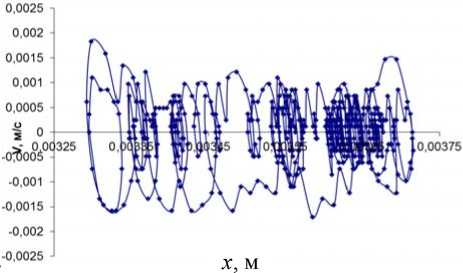
б
При этом вектор x ( t ) = ( x 1 , x 2 ) T совершал хаотические движения в пределах этих квазиаттракторов (их S ). Анализ всех полученных значений S представляет схожую картину в виде данных для каждого испытуемого: отдельно для неспортсменов и спортсменов. Подчеркнем, что статистическая обработка данных всей группы не имеет смысла (постулат теории хаоса-самоорганизации), и мы производим сравнения для каждого испытуемого отдельно именно его площади квазиаттракторов (табл. 1), так как имеем хаотический калейдоскоп статистических функций распределения f ( x i ) .
В табл. 1 представлен пример значений площадей квазиаттракторов S выборок треморограмм испытуемых 1 (неспортсмен) и 2 (спортсмен) для одной из серий эксперимента: до и после локального холодового воздействия. Уже из одной серии опытов легко видеть, что S для квазиаттракторов демонстрируют различия значений до и после локального холодового воздействия. При расчете среднего значения площадей квазиаттракторов ( < S > ), пример на рис. 2, и стандартного отклонения (о, ± ), в представленном примере с двумя испытуемыми были получены следующие данные: среднее значение площадей квазиаттракторов < 5 > испытуемого 1 до локального холового воздействия равно < S 1 > = 0,61 ∙ 10–6 (σ = 0,38 ∙ 10–6 у.е.), а после < S 2 > = 1,53 ∙ 10–6 (σ = 1,08 ∙ 10–6 у.е.). В случае с испытуемым 2 среднее значение площадей
Таблица 1
Площади ( S ∙ 10–6) фазовых плоскостей выборок треморограмм испытуемых
Следует отметить, что при проверке на соответствие вида распределения полученных данных площадей S обоих испытуемых ( n = 15) при многократных повторах до холодового воздействия имеется ненормальное распределение, т.е. мы использовали непараметрические распределения. Медианное значение ( Ме ) S испытуемого 1 в спокойном состоянии равно 0,48 ∙ 10–6 (0,23; 1,75) у.е. и испытуемого 2 – Ме = 0,31 ∙ 10–6 (0,14; 0,71) у.е. При внешнем воздействии (холодовом) увеличивается доля стохастики, и у обоих испытуемых распределение площадей нормальное.
Одновременно с расчетом площадей квазиаттракторов мы применили и метод расчета матриц парного сравнения выборок треморограмм, которые получаются у одного и того же испытуемого (находящегося в неизменном гомеостазе) в режиме многократных повторений ( n = 15). Для каждого испытуемого строились две матрицы (до и после воздействия стресс-агента) по 15 измерений (выборок) в каждой, в результате для одной матрицы получалось 105 независимых пар сравнения. Среди полученных 105 пар сравнения находились пары, которые при сравнении по критерию Вилкоксона имели уровень значимости ( p ) больше 0,05, т.е. p > 0,05. Это означает, что такую пару треморограмм можно отнести к одной генеральной совокупности (эти две выборки статистически совпадают, они одинаковые с позиции стохастики).
Для наглядного представления мы приводим два характерных примера (табл. 2 и табл. 3), в которых k1 = 3 для испытуемого 1 (спокойное состояние, табл. 2) и k2 = 9 после стресс-воздействия (табл. 3). Это характерный пример для испытуемых, которые не занимаются регулярно физическими нагрузками и у них всегда различаются k1 (до охлаждения) и k2 (после охлаждения кисти), т.е. имеют немного завышенные значения, чем у спортсменов. Последние в нашем примере (см. табл. 4 и 5) дают значение числа k пар совпадений треморограмм до воздействия k3 = 2 (табл. 4) и после k4 = 6 (табл. 5), т.е. несколько более низкие у спортсмена, чем мы это наблюдаем в предыдущих матрицах (см. табл. 2 и 3) у лиц без физической подготовки.
В целом при использовании непараметрического парного сравнения с помощью критерия Вилкоксона для каждого испытуемого были получены четыре таблицы, в которых представлены результаты расчета матриц (15 х 15) парного сравнения треморограмм N = 15, n = 15. Динамика непроизвольных микродвижений конечностей (тремора пальцев рук) как реакция на стресс-агент (в нашем случае локальное гипотермическое воздействие) проявлялась в изменении числа совпадений пар выборок ( k ), которые можно отнести к одной генеральной совокупности. Представленные матрицы парных сравнений в табл. 2–5, в которых количественной мерой является число совпадений пар выборок ( k ), для обоих испытуемых в спокойном состоянии и после локального холодового воздействия (всего 450 выборок треморограмм у обоих испытуемых) являются фактически средними (по результатам k ) матрицами из всех четырех наборов (серий по 15 матриц), значит < k 1 > = 3; < k 2 > = 6; < k 3 > = 2; < k 4 > = 6.
Наш пример, когда число увеличивается с k 1 = 3 совпадений в спокойном состоянии до k 2 = 9 совпадений после локального холодового воздействия у испытуемого 1 и с k 3 = 2 до k 4 = 6 у испытуемого 2 является характерным для всех наших измерений. Таким образом, локальное холодовое воздействие приводит почти к двух- или трехкратному увеличению числа пар совпадений ( k ) у мужчин вне зависимости от их физической подготовки.
Таблица 2
Матрица парных сравнений 15 выборок треморограмм испытуемого 1 до локального холодового воздействия (число пар совпадений k 1 = 3)
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
1 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,87 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
2 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,15 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
3 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
4 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
5 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,03 |
0,00 |
0,00 |
0,00 |
|
|
6 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
7 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
8 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,01 |
|
|
9 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
10 |
0,00 |
0,15 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
11 |
0,87 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
12 |
0,00 |
0,00 |
0,00 |
0,00 |
0,03 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
13 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,05 |
0,00 |
|
|
14 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,05 |
0,00 |
|
|
15 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,01 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
Таблица 3
Матрица парных сравнений 15 выборок треморограмм испытуемого 1 после холодового воздействия (число пар совпадений k 2 = 9)
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
1 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,31 |
0,00 |
0,75 |
0,00 |
0,00 |
0,00 |
0,63 |
|
|
2 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
3 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
4 |
0,00 |
0,00 |
0,00 |
0,64 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
5 |
0,00 |
0,00 |
0,00 |
0,64 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
6 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,22 |
0,00 |
0,00 |
|
|
7 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,83 |
0,01 |
0,00 |
0,00 |
0,00 |
0,00 |
0,38 |
0,00 |
|
|
8 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,83 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,01 |
0,01 |
|
|
9 |
0,31 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,01 |
0,00 |
0,00 |
0,17 |
0,00 |
0,00 |
0,00 |
0,01 |
|
|
10 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
11 |
0,75 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,17 |
0,00 |
0,00 |
0,00 |
0,00 |
0,69 |
|
|
12 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
13 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,22 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
14 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,38 |
0,01 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
15 |
0,63 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,01 |
0,01 |
0,00 |
0,69 |
0,00 |
0,00 |
0,00 |
Таблица 4
Матрица парных сравнений 15 выборок треморограмм испытуемого 2 до локального холодового воздействия (число пар совпадений k 3 = 2)
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
1 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,17 |
|
|
2 |
0,00 |
0,88 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
3 |
0,00 |
0,88 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
4 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
5 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
6 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
7 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
8 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
9 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
10 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
11 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
12 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
13 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
14 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
15 |
0,17 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
Таблица 5
Матрица парных сравнений 15 выборок треморограмм испытуемого 2 после локального холодового воздействия (число пар совпадений k 4 = 6)
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
1 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,10 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
2 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
3 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,09 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
4 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,67 |
0,15 |
|
|
5 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
6 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
7 |
0,00 |
0,00 |
0,09 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,34 |
0,00 |
0,00 |
|
|
8 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
9 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
10 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
11 |
0,10 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
12 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,10 |
0,00 |
|
|
13 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,34 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
|
14 |
0,00 |
0,00 |
0,00 |
0,67 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,10 |
0,00 |
0,00 |
|
|
15 |
0,00 |
0,00 |
0,00 |
0,15 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
Обсуждение
Новая методика расчета матрицы парных сравнений выборок позволяет оценить влияние локального холодового воздействия на функциональные системы организма, но эта оценка сильно варьируется, и она требует многократных повторов экспериментов. В наших наблюдениях для каждого испытуемого мы производим 15 серий исследований по 15 повторов измерений треморограмм в каждой серии. Это требует огромного времени и весьма трудоемких вычислений, которые связаны с расчетом всех 225 выборок треморограмм ( N∙n = 15 ∙ 15 = 225) для каждого испытуемого. В результате таких расчетов мы получаем выборки уже самих чисел k (пар совпадений выборок треморограмм). Очевидно, что любое число k i из серии N = 15 не может нам представлять среднее значение k для данного испытуемого, и поэтому одна серия не может представлять общие результаты измерений.
Однако простое измерение разовой выборки треморограмм и их традиционный статистический расчет теперь уже становятся бесполезными, так как такая (разовая) выборка будет уникальной (неповторимой) и мы по ней не можем судить о динамике изменения двигательных функций испытуемых, находящихся в условиях стрессовых (холодовых) воздействий. Поэтому все выборки разные (не менее 10% пар треморограмм не могут показать статистическое совпадение), следовательно, совершенно непонятно, что брать за изменение под действием холода, если без холодового воздействия все подряд полученные треморограммы у одного испытуемого (находящегося в одном гомеостазе) и так существенно различаются. Гипотеза Н.А. Бернштейна реализовалась в эффект Еськова–Зинченко (нет совпадений подряд получаемых выборок).
Для выхода из возникшего процесса в биомеханике и психологии мы предлагаем производить повторы измерений и рассчитывать матрицы парных сравнений выборок до воздействия и после него (у нас это было локальное охлаждение).
Однако более простой способ – это расчет параметров площадей фазовых плоскостей треморограмм. Во всех нами выполненных исследованиях тренированные испытуемые (спортсмены) всегда показывали меньшее значение площадей квазиаттракторов треморограмм, чем лица без специальной физической подготовки. В наших примерах средняя площадь < S 1 > для квазиаттракторов у треморограмм неспортсмена почти в 2 раза больше, чем средняя площадь < S 3 > у спортсмена (< S 1 > = 0,61; < S 3 > = 0,34), медианы дают несколько меньший эффект, но он тоже значителен (0,48 и 0,31 соответственно).
Аналогичную (и устойчивую) картину различий дают площади S для квазиаттракторов у треморограмм испытуемых после холодового воздействия. Здесь < S 2 > = 1,53 у неспортсмена и < S 4 > = 0,84 у спортсмена, размеры площади квазиаттракторов количественно представляют реакцию нервно-мышечной системы на стресс-воздействие (локальное охлаждение). Расчет параметров квазиаттракторов является весьма эффективным методом в биомеханике для оценки особенностей регуляции двигательных функций (в нашем примере это были непроизвольные движения в виде постурального тремора). Отметим, что такой подход дает реальную количественную оценку состояния нервно-мышечной системы, работы всей системы организации движений, которую еще 70 лет назад наш выдающийся предшественник Н.А. Бернштейн пытался сформулировать в качестве гипотезы «о повторении без повторений».
Таким образом, расчет матриц парных сравнений выборок и параметров квазиаттракторов для треморограмм дает возможность не только оценить стационарное состояние гомеостаза (у нас на примере нервно-мышечной системы), но и различать эти стационарные состояния гомеостаза между отдельными испытуемыми. В нашем случае речь идет о гомеостазе спортсменов и лиц без специальной физической тренировки. Мы сейчас демонстрируем, что число пар k совпадений выборок треморограмм в матрицах (см. табл. 2–5) различается для спортсмена и неспортсмена. Одновременно, мы наблюдаем и выраженные изменения в числах k 2 и k 4 у разных испытуемых после холодового воздействия на нервно-мышечную систему. При этом однонаправленно изменяются значения площади квазиаттракторов, которые в спокойном состоянии у спортсменов всегда имеют более низкие значения, чем у лиц без специальной физической подготовки. Расчет матриц и квазиаттракторов дает новый и эффективный метод диагностики состояния испытуемых, находящихся в различных физиологических и психических состояниях. На фоне статистического хаоса выборок треморограмм мы можем наблюдать определенные закономерности в рамках теории хаоса – самоорганизации.
Заключение
Прослеживается динамика увеличения площадей фазовых плоскостей после локального холодового воздействия в 2,5 как у неспортсменов, так и у спортсменов. Прослеживается трехкратное превышение k 2 и k 4 по отношению к k 1 и k 3 , что характеризует различия между свободным состоянием и треморограммами после локального холодового воздействия у испытуемых. При этом различия в значениях k не зависят от физической подготовки.
Благодарности
Работа выполнена при поддержке гранта РФФИ №15-41-00034 р_урал_а «Разработка новых информационных моделей и вычислительных алгоритмов для идентификации параметров порядка в описании и прогнозах сложных медикобиологических систем».
Список литературы Хаотическая динамика параметров треморограмм в условиях стресс-воздействий
- Веракса А.Н., Горбунов Д.В., Шадрин Г.А., Стрельцова Т.В. Эффект Еськова-Зинченко в оценке параметров теппинга методами теории хаоса и самоорганизации и энтропии // Сложность. Разум. Постнеклассика. - 2016. - № 1. - С. 17-24.
- Еськов В.М., Зинченко Ю.П., Хадарцев А.А., Филатова О.Е. Основы физического (биофизического) понимания жизни // Сложность. Разум. Постнеклассика. - 2016. - № 2. - С. 58-65.
- Зилов В.Г., Еськов В.М., Хадарцев А.А., Еськов В.В. Экспериментальное подтверждение эффекта «Повторение без повторения» Н.А. Бернштейна // Бюллетень экспериментальной биологии и медицины. - 2017. - № 1. - С. 4-9.
- Зинченко Ю.П., Хадарцев А.А., Филатова О.Е. Введение в биофизику гомеостатических систем (complexity) // Сложность. Разум. Постнеклассика. - 2016. - № 3. - С. 6-15.
- Филатов М.А., Веракса А.Н., Филатова Д.Ю., Поскина Т.Ю. Понятие произвольных движений с позиций эффекта Еськова-Зинченко в психофизиологии движений // Сложность. Разум. Постнеклассика. - 2016. - № 1. - С. 24-32.


