Характеризации типа ВМО, диагональное отображение и ограниченнность интегральных операторов в некоторых пространствах аналитических функций
Автор: Шамоян Роми Файзоевич
Журнал: Владикавказский математический журнал @vmj-ru
Статья в выпуске: 2 т.9, 2007 года.
Бесплатный доступ
Распространены (в различных направлениях) некоторые известные ранее характеризации аналитических классов Бесова и неравенства для рациональных функций, дополнены утверждения о диагональном отображении новой теоремой, обобщены классы F_s^{p,q} теоремы о действии операторов типа Чезаро.
Интегральные операторы чезаро, голоморфные пространства лизоркина --- трибеля, классы харди
Короткий адрес: https://sciup.org/14318212
IDR: 14318212 | УДК: 517.98
Текст научной статьи Характеризации типа ВМО, диагональное отображение и ограниченнность интегральных операторов в некоторых пространствах аналитических функций
Основная цель настоящей заметки распространить результаты о характеризациях типа ВМО классов Бесова и Блоха, полученные в [1, 2], дополнить утверждения об оценках рациональных функций и известные результаты о диагональном отображении из [3, 8], а также обобщить на голоморфные пространства Лизоркина — Трибеля недавно полученные утверждения об ограниченности операторов типа Чезаро из [4].
Для формулировки теорем, установленных нами, введем стандартные обозначения. Всюду ниже D — круг на комплексной плоскости C, D = { z : | z | < 1 } , T — его граница, T = { z : | z | = 1 } . н p (D) — класс Харди [5], H p (D) = { f е H (D) : || D t f || h p < ro} , где H (D) — класс всех голоморфных в D функций, t Е R, 0 < p 6 ro , (Df)(z) = P (k + 1) t a k z k , t Е R, f (z) = P a k zk . Легко видеть (Df )(z) = (zf (z)). Всюду ниже k > 0 k > 0
B p α — аналитические пространства Бесова [11]:
B α p
< f Е H (D) : k f IB = j D t f (z) [ (1 - | z | ) ( t - a ) p -1 dm 2 (z) < ro > ,
D где a, t, p Е R, t > a, 0 < p < ro.
Теорема 1. Пусть t + 1 < p < ro, (s — a)p = 1 + в + Y, t < 1, s > a + 1, в, Y > 0, причем t = в или t = Y • Тогда следующие условия равносильны:
-
1) f Е B a ;
-
2) J = JR
DD
( D s-1 f ) ( z ) - ( D s-1 f ) ( w )
z - w
p
(1 — | z | ) e -1 (1 — | w | ) Y -1 dm 2 (z) dm 2 (w) < ro .
<1 2) ^ 1): Основная идея — привлечь диагональное отображение. Действительно, импликация 2) ^ 1) — непосредственное следствие теоремы о диагональном отображении, доказанной в [8]. Функция G , где
G(z, w) =
Г f (z)-f ( w ) z - w ,
1 f 0 (z),
z = w, z = w
— аналитическая функция в бидиске в D 2 = D х D [8], а теорема о диагональном отображении утверждает [8, 14], что Diag A a (D n ) = A an +2 n - 2 (D), где Diag f = f (z, ...,z), a > 1, 0 < p < to , n E N, а A a (A a = B p , a = — вр — 1, в < 0) — классы Бергмана. Для доказательства обратной импликации нам понадобятся несложные операции с формулой проекции Бергмана.
Следующее равенство выводится непосредственно из формулы проекции Бергмана [8]:
| F (z,w) | =
D s -1 f (z) - D s -1 f (w) z - w
= C
(V)/
D
~ V+1 T,
D Ds-^f (ге)(1 - |W| ) V w
— wz) (1
- ww
dm 2 (го)
( ( io S г \ Г(к + s + 1) k
I D f) (z) = S r(k + s) a k z -
\ k > 0
f= akzk k>0
Для достаточно большого t и V, близкого к — 1, V > — 1, имеем:
e t +1 e t +1
D z D w F(z,w)
= C (V) /
D
~ V+1 - _
D D^-1f (W)(1 — |t0 | ) V w
Л - V+2 Л - V+2
I 1 — wz I 11 — wz I
dm 2 (га)
и
J-=//
DD
t +1 t +1 p
Dz Dw F(z,w) (1 — |z|)(1+t)p+e-1 х х (1 — |w|)(1+t)p+Y-1 dm2(z)dm2(z) 6
6 c// /( I De V + s f (w) Г (1 — | z | ) VP (1 — | w | ) p ( t +1)+ Y -1 (1 — | z | ) e - 1+ p ( t +1) - ep
DDD
^11 — to | 11 — tow | ^ dm 2 (га) dm 2 (z)dm 2 (w) 6
6 C j |DDV+sf (w |p (1 — |w-|)(s-a)p-1+Vp dm2 (г0) -D в силу известных оценок
6 C
D
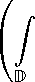
| f (w) | (1 — | w | ) V dm 2 (w) \ p | 1 — wz l a | 1 — wz 1 | 2+ e J
| /(w)П1 -j wD VpX 1-_kD - p dm2^w)
| 1 — t5z | pa | 1 — wz - | - p +2+ ep
p > 1, a-в > 0;
f (1 — | w | ) u dm 2 (w) 6 C
J | 1 — wz | Y (1 — | z | ) Y - u -2
D где u > —1, y > u + 2, z, z1 E D, e > V, f j If (w)l (1 — ЫГ dm2(w)^ 6 C j |f (w)|p (1 — |w|)ap+2p 2 dm2(w), p 6 1, DD
приведенных, например, в [7, 8, 17, 19].
Остается применить известную теорему Харди — Литтлвуда о действии производной в пространствах Бергмана, точнее ее вариант для дробной производной, легко выводимый из классической теоремы Харди — Литтлвуда [5, с. 81] слева и справа в (3):
J 6 CJ 1 6 C 1 k f k P a . p
Меняя в (4) z и z i , мы восстановим симметрию в индексах. B
Замечание 1. Теорема 1 распространяет в двух направлениях утверждение, установленное в [2, теорема 3]. Рассуждение, приведенное в [2] — доказательство характеристики типа ВМО (инвариантных относительно преобразования Мебиуса) 1
классов B p , p > 2 в части необходимости и в части достаточности существенно использует свойства этого преобразования. Наши рассуждения, на наш взгляд, существенно проще.
Замечание 2. Приложения различных характеристик типа ВМО классов Бесоа известны [9, 10, 22].
Замечание 3. Если а = 1/p, p > 2, s = 1, в = Y = р/2 — 1, то мы получаем в точности теорему, установленную в работе [2].
Подход, основанный на диагональном отображении, позволяет доказывать различные утверждения подобного рода. Следующая теорема распространяет результат из [1], где получен частный случай теоремы 2 при в = 1, а = 1.
Теорема 2. Пусть 0 < а < 1, t, V > 0, t + V = а, в — любое действительное число,
∞ , ∞ α, β
< f E H (D) : sup M ^ ( d e f,rA (1 — r) a < го
I r e (a ,i) v 7
Тогда f ∈ A α ∞ , , β ∞ если и только, если
S = sup sup r, R |w|=r, |z|=R
D e -1 f) (w) — (П e -1 f) (z)
z - w
(1 — R) t (1 — r) V < го .
C Достаточность условия (7) тривиальна (при этом надо учесть, что
(Df) (z) = (zf(z)) 0 = zf 0 (z)+ f(z)).
Для доказательства необходимости мы снова воспользуемся равенством (1).
Имеем
J = sup sup
| z | | w |
((1 -| z | ) t 1 + t (1 -| w | ) t 2 + V
t 1 e t 2
D w D z
(
D e -1 f (z) — D e-1 f (w) z - w
6 c(V ) sup
| z | , | w |
/
D
DV + e f (t)(1 - | w ! ) V w
1 V2 +1 Л V1 +1
1 - wz 1 - ww
dm 2 (w)
(1 -| z | ) t 1 + t (1 — | w | ) V + t 2 6
(
sup
| z | , | w | , | w | < 1
M^\DV +e f, l w
e
(1 - |w| ) V +a
)
X
X
(i i w i ) " :i i zii zi i wT- " 2
I l t 2 +1 1 l t 1 +1
1 - wz 1 - ww
dm 2 (w) = S
(t + V = a, V — достаточно большое число). Учитывая оценку (8) и оценку последнего интеграла [7], получим
S 6
(1 — Н) ‘ (1 -M) V | 1 — zw | t | 1 — zw l V
6 const,
0 < t 2 + a < 1, 0 < t 1 + a < 1, t 1 + t 2 + a > 0 (мы на последнем шаге использовали теорему Харди — Литтлвуда о действии производной [5, с. 87] справа и слева в (8)).
Замечание 4. Аналогичные утверждения можно вывести и для производных (обычных) f ( n ) (z). Но доказательства этих предложений технически несколько сложнее.
Подобный подход можно использовать и для классов функций с «нестандартной» квазинормой. Здесь снова (по крайней мере) половина критерия будет получена, если будет установлена надлежащая теорема о диагональном отображении. Ниже мы покажем это на примере пространств
D V Т Р.» = ' е D V : f е т’в},
где a > 0, в > — 1
/\ 1/p
If1
Т Рв (D) = W е H (D) : sup (1 — p) a / i f (pR^) l p (1 — R) e dm 2 (R^)
, p^O,1))
< го
Определение 1 [8]. Пусть H (D n ) — пространство всех голоморфных в полидиске D n функций, D n = { z = (z 1 , z 2 ,..., z n ), i z j | < 1, j = 1,...,n } , X C H (D n ) — подпространство H (D n ). Скажем, что след класса X на диагонали поликруга совпадает с Y , Y C H (D), Y — подпространство H (D), если для любой функции f е X f (z,..., z) G Y и для любой функции g G Y существует функция G G X, такая, что G(z,..., z) = g(z). При этом будем использовать обозначение DiagX = Y . Задача о диагональном отображении в H p (D n ) рассматривалась многими авторами [8, 14].
Незначительно модифицируя доказательство из [8] (рассуждения следует применять к функциям f p , g p , р G (0,1)), нетрудно установить следующий результат.
Предложение С. Пусть а > 0, n Е N, 0 < p < го . Тогда
Diag A , = т а в (D) = Ь Е H (D) : sup (1 - р) а х [ р е (0 , 1)
/ \ 1 /p
х
I У If (pRO\P (1 - R)e RdR^m(0 I в = n — 2, n > 1.
D
A p = b Е H (D n ) : sup M p (f,r)(1 — r) a < го I , I r e (0 , i) )
M
p
(f,
r) =
M
p
(f,r,...,r),
0
го
, а >
0.
Из предложения С следует оценка (
\
w
\
=
\
z
\
= r)
i/p suP (1 — Р)а pe(0,i) p
/ \Df
f
(pR<)
\
RdRdm
(£)
D
6
c
sup
r
De
e
-1
f) (z)
—
(De
e
-1
f) (w)
z
—
w
p
dm(^)
dm
(у) I (1
—
r)
a
.
Обратная оценка выводится как и выше из (1)–(3) путем несложных преобразований. Пусть
p
6
1, t
i
, t
2
> 0, t
i
, t
2 —
достаточно большие положительные числа. Тогда из (1) и (6) имеем
(1 — p)
Pa
+(
t
1
+
t
2
)
P
у
T
2
D
t
1
D
t
2
D
e
-1
f (р^)
—
D
e
-1
f
(ру)
Ру
—
Р<
p dm (£) dm (у) 6 6 c(V) Я/
T
2
D
\
d
V
+
в
f (pw)
I
(1
— \
ге
\
)
V
\
w
\
dm
2
(га)
I I t1 + 1 I _. |t2+1 p
(1
—
p)
pa
+(
t
1
+
t
2
)
p
dm
(£)
dm
(у)
6
M.
Применив дважды теорему Харди — Литтлвуда [5, с. 87], получим c
M
6
c(V
V
D
ID
V
+
в
f (рге) |
P
(1
—
\te
\
)
Vp
+2
p
-2
dm
2
(w) (1
—
\
w
\
p)(t
1
+r)p-1
(1
—
Ир)^1
)*-1
t
1
+
t
2
D D^v f (pRO
(1
—
Р)
pa
+(
t
i
+
t
2
)
p
p
(1
—
R)
Vp
RdRdm
(^) (1
—
p)
(
t
1
+
t
2
)
p
(1
—
p)
pa
6
c
k
f
k
D
e
A
p
α
При этом, чтобы «избавиться» от t
1
, t
2
слева необходимо потребовать в >
p
+
а
—
1 [22]. Случай
p >
1 расматривается аналогично с привлечением оценки (4) вместо (6).
Итак, нами установлена Теорема 3. Пусть а > 0, в Е R, в > p+2-1, 0 < p < го. Тогда f Е DвТРо если и только, если sup re(0,1)
De
в
1
f (r^)
—
Dв
1
f (гу)
r^
—
гу
dm
(^)
dm
(у) (1
—
r)
a
<
го
.
Заметим, что справедливо и обратное. Опираясь на утверждение о характеризациях классов голомрфных функций через разности
(
Dtf
)
(z)-
(
D
t
f
)
(
w
)
z
-
w
можно полностью описывать следы тех или иных функциональных классов в бидиске на диагонали (z, z). Действительно,
, X
(
D
-1
f
)
(z)-
(
D
-1
f
)
(w)
функция
F (z,w)
^-w —
дает искомое продолжение.
Имеем
F (z,z)
=
(d
1
f
) (z) =
f
(z), где (Ъ
1
f
) (z)
неравенства следуют непосредственно из теорем 1 и 2: z
=
J f (w)dw
и следующие
sup
\
F(z,w)
|
(1
- \
z
\
)
V
(1
- \
wD
t
6
c
k
f
Ha^
,
a >
o, t +
V
=
a-
|z|<1, |w|<1 0'“ j j\F (z,w)\p (1 -\z\)e 1 (1 -\w\)Y 1 dm2(z) dm2(w) 6 c kf Hb^ , где p > 1 + y, в < 1, a 6 -1, в, Y > 0, (-ap) = 1 + в + Y• Обратное к последнему неравенству при любом n ∈ N получено в [8]. А неравенство sup sup (\f(z,z)l (1 - \z\)V+t) 6 ci sup (\f(z,w)l (1 -|zDV (1 - \w\)t),
0
где V,
t >
0, очевидно.
Предположим далее, что всюду ниже R(z) — рациональная функция степени n,
n
= 1, 2,..., полюса которой лежат вне диска D,
Bl
— класс Блоха,
Bl = If
G
H
(
D
) :
||f
k
Bi
= sup |f
0
(z)| (1
- \
z
\
)<
to
I .
|
z
|
<
1
Мы установим, что имеет место оценка α
1
/a
/ |D
a
+1
R (p^)
|
dm
(^) (1
-
p)
a
6
n
a
k
DR
k
Bl T для всех a, 0 < a < to.
Отметим, что при
a >
1 эта оценка установлена Пекарским [3]. Нам понадобится в дальнейшем следующая векторнозначная максимальная теорема.
Теорема А [6]. Пусть X — квазинормированное пространство. Тогда sup zer(?)
k
f (z)
k
x
dm
«)
6
c
(X)
j
k
f
(O
k
x
dm
«),
Г«) = {z :|1
-
Iz
l
< (1
-\
z
\
)} .
T
А. Пекарский в [3] для
a
6
1 вывел следующие два неравенства:
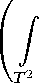
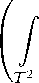
Список литературы Характеризации типа ВМО, диагональное отображение и ограниченнность интегральных операторов в некоторых пространствах аналитических функций
- Holland F., Walsh D. Criteria for membership of Bloch spaces and it is subspace BMOA//Math. Ann.-1986.-V. 273.-P. 317-335.
- Stroethoff K. The Bloch spaces and Besov spaces of analitic functions//Bull Austr. Math. Soc.-1996.-V. 54.-P. 211-219.
- Пекарский А. А. Новое доказательство неравенства Семмеса для производных рациональных функций//Мат. заметки.-2002.-Т. 2.-С. 230-236.
- Aleman A., Cima J. An integral operator on H^p and Hardy's enequality//J. D'Analise Math.-2001.-V. 85.-P. 157-175.
- Duren P. L. Theory of H^p spaces.-N-J; London: Acad. press, 1970.
- Alexandrov A. B. Essays on non Locally convex Hardy classes//Lecture Notes in Math.-1981.-V. 864.-P. 1-90.
- Шамоян Р. Ф. Обобщенное преобразование Харди и операторы Теплица в пространствах типа ВМОА//Укр. мат. журн.-2001.-Т. 9, № 53.-С. 1206-1271.
- Djrbashian, Shamoyan F. Topics in the theory of A^p_{\alpha} spaces//Teubner Texte zur Math.-1988.-V. 105.-P. 199.
- Boe B. Interpolating sequences for Besov spaces//J. of Func. Anal.-2001.-V. 192.-P. 319-341.
- Wu Z. The Predual and second Predual of \omega_{\alpha}//J. of Func. Anal.-1993.-V. 116.-P. 314-334.
- Шамоян Р. Ф. О характеристиках типа ВМО одного класса голоморфных в круге функций//Сиб. мат. журн.-2003.-Т. 44, № 3.-С. 539-560.
- Aleman A., Siskakis A. G. Integration operators on Bergman spaces//Indiana Un. M. J.-1997.-V. 46, № 2.-P. 337-356.
- Aleman A., Siskakis A. G. An integral operator on H^p//Complex Variables.-1995.-V. 28, № 11.-P. 149-158.
- Шамоян Ф. А., Ярославцева О. В. Непрерывные проекторы, двойственность диагональное отображение в весовых пространствах голоморфных функций со смешанной нормой//Зап. сем. ПОМИ.-1998.-Т. 225.-P. 184-197.
- Трибель Х. Теория функциональных пространств.-М.: Мир, 1983.-344 с.
- Ortega J., Fabrega J. Corona type decomposition in some Besov spaces//Math. Scand.-1996.-V. 78, № 1.-P. 93-111.
- Nakazi T. Canad Nath Bull.-1996.-V. 39, № 2.-P. 219-226.
- Dynkin E. Rational Function in Bergman spaces, Complex analisys, operators and related topics//Oper. Adv. Appl.-2000.-V. 113.-P. 77-94.
- Ortega J. M., Fabrega J. Holomorphic Triebel-Lizorkin spaces//J. of Func. Anal.-1998.-V. 151.-P. 177-212.
- Cohn W., Verbitski I. Factorization on tent spaces and Hankel operators//J. of Func. Anal.-2000.-V. 175.-P. 308-329.
- Wu Z., Xie C. Q_p spaces and Morrey spaces//J. of Func. Anal.-2003.-V. 164.-P. 1-15.
- Шамоян Р. Ф. О действии операторов свертки и Теплица в пространствах типа ВМОА//Мат. заметки.-2003.-Т. 73, № 5.-С. 759-772.
- Dyakonov K., Girela D. On Q_p spaces and pseudoanalityc extention//Ann. Acad. Sci. Fenn.-2000.-V. 25.-P. 477-487.
- Essen M., Xiao Some results on Q_p spaces 0
- Bonami A., Bekolle D. Inegalites a poids pour le noyay de Bergman C. R.//Acad. Sci. Paris Ser. A.-1978.-V. 286, № 18.
- Khavin V. On the factorization of analytic functions smooth up to the boundary//Zap. Nauchn. Sem. LOMI 22.-1971.-P. 202-205.
- Essen M., Wulan H. On analytic and meromorphic function and spaces of Q_p type//J. Math.-2002.-V. 46, № 4.-P. 1233-1258.
- Шамоян Р. Ф. О пространствах голоморфных в поликруге функций типа Лизоркина -Трибеля//Известия НАН Арм.-2002.-Т. 37, № 3.-С. 57-78.