Hardy type inequalities in classical and grand Lebesgue spaces lp), 0
Автор: Ouardani Abderrahmane, Abdelkader Senouci
Журнал: Владикавказский математический журнал @vmj-ru
Статья в выпуске: 2 т.26, 2024 года.
Бесплатный доступ
In 2020 Rovshan A. Bandaliev et al. proved the boundedness of Hardy operator for monotone functions in grand Lebesgue spaces Lp)(0,1), 0
Inequalities, quasi-monotone functions, hardy operators, grand lebesgue spaces, weighted lebesgue spaces
Короткий адрес: https://sciup.org/143182662
IDR: 143182662 | УДК: 517.9 | DOI: 10.46698/q9607-8404-0437-r
Текст научной статьи Hardy type inequalities in classical and grand Lebesgue spaces lp), 0
For 0 < p < от we denote L p , w (0,1) the set of all Lebesgue measurable functions, such that
/ 1
Ilf ^Lp,w (0,1) = Ilf llp,w = ( j \f (x)lp w(x) dxj < ю>C
\ 0/ where w E Ll°c(0,1) and w(x) > 0, a. e.
In 1992 T. Iwainiec and C. Sbordone [1] introduced a new type of function spaces Lp)(Q), 1 < p < to, where Q is a bounded open set Q C Rn, called grand Lebesgue spaces. Namely, the grand Lebesgue spaces are defined as the space of the Lebesgue mesurable functions f on Q such that
Ilf lip) = suP
0
(iQ Zlf(x,r* \ Q
dx
p-ε
< от ,
where | Q | is the Lebesgue measure of Q.
-
# This work is supported by university of Tiaret, PRFU project, code: COOL03UN140120180001.
(c) 2024 Ouardani, A. and Senouci, A.
These spaces were intensively studied during the last years due to different applications (see [2] and [3]) and continue to attract attention of researchers (see [4–6]).
We state the following definitions,proposition and corollary that are useful in the proofs of main results.
Definition 1 [7]. Let 0 < p C 1. We say that function f belongs to the grand Lebesgue space Lp)(0,1), if f is non-negative and Lebesgue measurable a. e. on (0,1) for which г/ If (x)|p-'
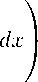
< X .
Il f llLp ) (0 , 1) = suP
0
Definition 2 [7]. Let 0 < p C 1. We denote by Ap the class of measurable functions f G Lp)(0,1), such that
Ilf II A p = sup
0
г У ( x p - s -1 — 1 ) f p - s (x) dx
1 p-ε
< X .
Remark 1. In [7] was proved that for 0 < p C 1, L p ) (0,1) is quasi-Banach function space over (0,1). In this case if w = 1, (1.1) becomes quasi-norm of usual Lebesgue space L p (0,1).
The following definition is well-known (see [8]).
Definition 3. We say that a function f is quasimonotone on ]0, x[ , if for some real number a, x a f (x) is a decreasing or an increasing function of x. More precisely, given в G R , we say that f G Q e if x - e f (x) is non-increasing and f G Q e if x - e f (x) is non-decreasing.
The following proposition was proved in [8].
Proposition 1. Let —x < в < +x and 0 < p C 1. (a) Let f G Qe, 0 C a < b C x for в > -1 and 0 < ■ If в = —1, then a < b C x for в C —1.
/ b \ p
( jf (t) dt l C p | в + 1 | 1- p
a
If в = — 1 , then
b
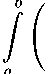
t e +1
—
t β
a ] f p (t) dt.
-
(1.2)
pb
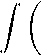
p- 1
f p (t) dt.
-
(1.3)
The inequalities hold in the reversed direction if 1 C p < x .
-
(b) Let f G Q e and 0 C a < b C x for в < - 1 and 0 C a < b < X for в ^ - 1 .
If в = — 1 , then
b
p
C p | в + 1 | 1- p
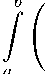
t e +1 — b e +1
t β
lj f p (t) dt.
-
(1.4)
If в = — 1, then
b \ p
У f (t) dt j
a
C p У (t In b ) f p (t) dt.
a
-
(1.5)
The inequalities hold in the reversed direction, if 1 C p < x .
-
(c) The constants in these inequalities are the best possible in all cases.
If in (1.2), (1.4), (1.3) and (1.5) we set a = 0, b = 1, a = 0, b = x , a = x , b = 1 and a = x , b =1 respectively, then we get the following corollary.
Corollary 1. Let 0 < p < 1 .
-
(a) If в > - 1 , f € Q e , then
1 \ p 1
f f (t) dt] ^ P |в + 1Р—У tp-1f p(t) dt.
-
(b) If в > - 1 , f € Q e , then xp x
У f (t) dt ] < p 1 в + 1 | 1- РУ ( t - e | t e +1 - x e +1 |) p f p (t) dt.
-
(c) If f € Q - 1 , then
(1.6)
(1.7)
{ 1 \ p
[ у f (t) dt ]
x
(d) If f € Q -1 , then
/ 1 \ p
I У f ( t ) dt ]
x
< p У ( t In | ) f p (t) dt.
x
< p У (t In b) f p ( t ) dt.
x
(1.8)
(1.9)
-
2. Main Results
The constants in these inequalities are the best possible.
Throughout the paper, we will assume that the functions are non-negative and Lebesgue measurable on (0,1). We consider the Hardy operators
x
(H 1 f )(x) = 1 У 0
f ( t ) dt,
1 (H2f) (x) = 1 У x f (t) dt.
Theorem 1. Let 0 < p < 1 , в > — 1 , w(x) = x p 1 — 1 , 0 < x < 1 and f € Q e . Then the inequality 1
IHf Hmw « [(в + i)1-p j^| p IlfIl„(0,1) (2-D holds, where [(в + 1)1-p ^p] p is the sharp constant (the best possible).
<1 By applying Corollary 1 (a), we obtain
I H 1 f I l p (0J) =
' 1 \ p / 1 / x \ p \ p
У (H 1 f) p (x) dx ] = 1 У x p 1 У f (t) dt ] dx ]
p
= ! xp I I f (t)X (0 ,x ) (t) dt] dx 00
p
1 1
: < p p (в + 1) p
" 1 / 1 \
/ x p I I fp^X^tW -1 dt ] dx
1 p
Now, by the Fubini theorem, we get
l H 1 f к (0 , 1)
1 1-p
< p p (в + 1) p f p (t)t
оp- 1
dt
p
—Ш ' (в+1)
1 \ p
[ f p (t)t p -1 ( 1 - t 1- p ) dt I
—Ш P <в+1) *
1 \ P
I( t p - 1 - 1 ) f p (t)dt j , 0
thus
»H1f k(0,1) <[(i-p) (' + 1)1-p] p llf Il,.(00) • p-1
Let f (x) — (в + 1) P хв. Indeed, lH1f Имо,1) =
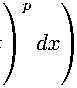
p -1
(в + 1) P
p tβ dt dx
p
p -1
— (в + 1) P I / x -
T (e+1)p \ p p x dx
(в + 1) p
— (в + 1) P ( I
1 \ P xβp dx
— (в + 1) - p ( ) P
\ 'p + 1/
and
llf \\lp, w (0 , 1) -
1 \ P
I ( t p-1 - 1 ) f p (t) dt j 0
1 \ P t (tp-1 -1) (в + 1)p-1tep dt I
so
p-1
— (в + 1) P
- t ep )"j — ( в +1)“ ( ...
-"■ •"“ KnoW l^r-
1 \ P
'p + 1)
I ( в +1) 1
-p
p llf BLp,w(0,1)
К 1 У1' ■1, 1 T
p-1
(в + 1) P
(' p7(.+1П
1 \ p
'p + 17
-(в + 1) - 1 1P •
The proof is complete. >
Remark 2. If в = 0 in (2.1), we have Theorem 1 of [7].
Theorem 2. Let 0 < p < 1, в > - 1, w(x) = /J (1^в- 1)+1 dt and f ^ Q в • Then the inequality
W Hf W l ' (0 , 1) « ( p(в + l) 1- p ) 1 Il f W l ,,w (0 , 1) ■ (2-2)
holds, where (р(в + 1) 1 p) p is the sharp constant.
<1 By using Corollary 1 (b) and the Fubini theorem, we have p 1
W H 1 f W L p (0 , 1) = ^ x p ^/ f (t) d^ dx ^
1 1 — I
< p p (в + 1) p
1 1—p
= p p (в + 1) p
1 1—p г
= p p (в + 1) p Jf p (t)t 0
х в +1
-
t e +1
p- 1
f p (t) dt
dx
1 p
x e + - t e +1 )p f p (t) X (o, x ) (t) dt j dx
■ -в ( р-1) | [
t
1 p
x p ( x e +1 — t e +1 ) dx j dt
1 p
.
Let x = -, thus y, f p(t)t-e(p-1)
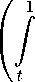
t p y p
( t e +1 y в 1 — t e +1 ) ty 2 dy j dt
1 1—p
= p p (в + 1) p j f p (t)t 0
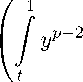
1 p
/ 1 — y e +1 V-1 к У в +1 )
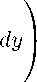
dt
1 1—p г
= p p (в + 1) p J f p (t) 0
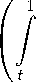
■—e(p - i) t — p+i t (e+i)(p - i)
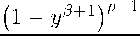
y e ( p -1) + 1
dy dt
1 1—p
= p p (в + 1) p
Wf W L p,w (0 , 1) ■
p — 1 o
Let f (x) = (в + 1) p х в . Indeed,
W H 1 f W l , (0 , 1) =
1 x p
У 1 У p—1 ~
~ I / (в + 1) ' t e dt j dx
1 p
= (в + 1) 'f
1 \ '
вp + 1)
and
II f kp,w (0,1) = (f (в + 1) Р -1 Х вР (/ \ 0 \x
1 p-1 = ( в + 1) p [J t e(p - 1)+1
p- 1
t e ( p- i)+i
1 ) p
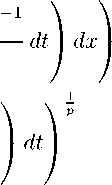
so
p-1 - 1
= (в + 1) p (вр + 1) p
p-1
= (в + 1) p
(вр + 1) p (в + 1) p
1 \ p j te (1 - te+1)p 1 dt )
1 1
( / (в + 1)t e ( 1 - t e +1 ) p 1 dt )
= № +1) 2- p (вр +1) ) - p ,
( р(в + 1) 1- p ) P I f ||
WM) = Ив + !) 1- p) p Ив + «’ —p (вр + 1))
- 1
= (в + 1) p (вр +1) p .
The proof is complete. >
Remark 3. If в = 0 in (2.2), we get Theorem 2 of [7].
Theorem 3.
Let
0
< p <
1
,
0
< a < ж, w(t) = (in (a ))p 1(1 — tp—^—p), 0
W Hf Lp(0 , 1) ^ ( 1 - p ) Ilf ^ L p,w (0 , 1) ,
(2.3)
holds, where ( ^^p ) p is the sharp constant.
<1 By applying Corollary 1 (c) and the Fubini theorem, we obtain
W Il L p (0,1) = (У (H 2 f) p (x) dx a
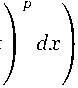
<
/ x ( p ht in ( at )) f p ( t ) dt )
ax
dx
1 p
= p p
У У in Q У f p (t) [ У x-p dx ) dt aa
1 p
= ( A)' (/ f ""1" ( a ))
p - 1 \p
( 1 — t p -1 a 1- p ) dt I ,
thus
W H 2 f W lp (0 , 1)
C
( p ^ p
1 - p
Ilf H L p,w (0 , 1) •
Finally, we obtain the required inequality.
We suppose that there exists C > 0, such that C C (1 -- p) p , thus C 1 = C p (1 - p) C p, then one can conclude that exists C i , C i C p , which contradicts the fact that p is the smallest possible in (1.8). >
Theorem 4. Let 0 < p < 1, 0 C a < b < ж , w1(t) = (ln (b))p 1, 0 < t < 1, and f G Q-1. Then the inequalty lH2f ^Lp(0,1)
C (Hhp) P I f " L p^ >.
(2.4)
holds, where (y—p) p is the sharp constant.
-
< The proof follows in view of Corollary 1 (d) and the rest is similar to that of Theorem 3. >
Now we lead with the Hardy operator in the grand Lebesgue spaces.
By Definition 1, we have 0 < p C 1 and 0 < E < 2 , thus 0 < p — E < 1, then one can apply Corollary 1 by replacing p by p — e . Consequently we get the following statements.
Corollary 2. Let 0 < p < 1 , 0 < e < 2 .
-
(a) If в > — 1, f G Q e and 0 C a < b C to , then
/ b \p— / b
I I f (У) dy I C (p - Е)(в + 1)1-p+e I I y fp-£(y) dy I .(2.5)
-
(b) If в > — 1, f G Q e , then
( jf(y)dy) C (p — Е)(в + 1)1-p+'j [y-e (xe+1 — ye+1)]’’-'-1 fp-'(y)dy.(2.6)
The constants in these inequalities are the best possible.
Theorem 5. Let 0 < p < 1 , 0 < E < p , f G A p and f G Q e , в ^ 0 . Then
IH1f lLp)(0,1) C C If H4 .(2.7)
If C > 0 is the sharp constant in (2.7) , then
(j—p p C C C (в + 1)p-1 (^) p.(2.8)
( 1 p — E
E [ I H 1 f ( t ) | p - e dt = sup
0
0 / 2
E /
x p-ε
x \ p— ■
У f (t) dt I dx
1 p-ε
.
By using Corollary 2 (a) with b = x, we obtain
\
H
1
f
\\lp
)(0,1)
<
sup (p
-
£
)
p-E
(
в
+1)
-pp— p)
’
0
= sup (p — £) p - E
0
1 - p+E (в + 1) p - E
-
= sup (p — £) p-E
0<£< —
1-p+E / (e + 1) 2 (
sup
0
(
p - £
1 + £ -
x
1 p-ε
tp £ 1 f p 5 (t)x (0 , 1) (t) dt dx
£ J t p - 5 -1 f p - 5 (t)
1+ £ - p
) p - E 1 - p+E
(в + h
1—p+E
< sup (в + 1) P — e sup
0
p
\ 1 +
- £
p-ε
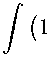
t 1+ £ - p) t p
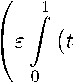
1 p-ε p-£-1 — 1) fp-£(t) dt I sup 0 1 p-ε (tp-£-1— 1) fp-5(t) dt I t x£ pdx di 1 p-ε 1 p-ε 5-1fp-£(t) dt . Let 0 < £ < p, thus 1 — p + £ < 1 — p + p = 1 — p, therefore 1 p+e< 2— 1. 2, p-5 p Since the function £ H l(£ = (i+--p)p-Eis decreasing on interval (0, 2), then we obtain IH1f \\lP)(0,1) < (в + 1) p 1 fe)p Ifu- One can deduce that C<(в+1) p-1(1—p)p On the other hand, let us proved the left hand side of (2.8). Let f (x) = в + 1, thus and sup £p-E(в + 1) 0 i < sup £p-E 0 sup 0 ( p-£ £ - p + 1 p-£ If Iap = 1(в + 1)Ia = sup p p 0<< — . p-e-1 (x; p-ε = p-ε 1) (в + 1)p-5dx sup £p-E(в + 1) 0 )p1■ (в+1)= \H1f\lp)(0,1) = |н1(в + 1)|p) = 0<upp £ / xp £ - p + 1 p-£ ^ p~E sup £p-E 2^"^^ (в + 1), 0 x p — 5 p-ε (в + 1)dt dx then by (2.7) ^H1f HLp)(0,l) " IlflU) sup Ep e (в + 1) ■te:)’■ 0<-< 2 ~"2 sup E ~ C-p^ p (в + 1) 0<-<2 V 7 The proof is complete. > Remark 4. If в ■ 0 in (2.8), we have Theorem 3 of [7]. Theorem 6. Let 0 < p < 1, 0 < e< |, w(t) ■ §1 (1~вв:Е-1+^ dy, 0 < У < 1, and f E Qв, в ^ 0. Then the inequality IHlf «L„(0J) < C Ilf Ik,,,. (0,1) . (2.9) holds, where 1 »fk, ..«w ■ ■■2(ej (j(1 yXX-1 dy) fp-'(t)dt) ■ If C > 0 is the sharp constant in (2.9), then (2) p « C « ((в + 1)1-2p)p ■ (2.10) * IHlf»Lp,(0,1) ■ sup 0<-< 2 |Hif ■ ' dt p-ε ■ sup 0<-< p - 1 / x \ p-- - EI xP— (If (t) dt 00 p-ε According to Corollary 2 (b) and the Fubini theorem, we have IH1f l|Lp)(0.1) < supp 0<-< p 1x E / x— ((p _ Е)(в + 1)1-P+-/ xe+1 ^^^^^v te+\) r-11 X fP -(t)X(0,1)(t) dt dx ■ sup ((p - Е)(в + 1)1-p+-) p-e 0<-< p E У f P--(t)t-e(p---1) - 1 p-ε Let x ■ -, then y, E I f p--(t)t-e(p---1) — te+1) x- p dx | dt e+1 E j fP--(t)t-e(p---1) (/(0 — te+1 dt so tJf p-'(t)t-e(p-'-1)t(e+1)(p-' -1)t'-p+1(/ ((1)e+1-1) p' 11)'-p( 7) dyh 1 t у f p-'(t) . 0 t / f p-'(t) 1 p-ε 1 (1 - ув+1)р-^-1 \ J у(в+1)(р-'-1)+'-р+2 dy I t } (1 - ув+np--1 \ dy dt J ув(р—'—1)+1 y I t IIH1fIlLp)(0,1) < sup ((P - t)(в + 1)1 p+') p—E o<'< 2 < pp ((в + 1)1-2) p sup v 7 o<'<2 In the right hand side of (2.9), it’s obvious that y G]0,1[; (1 - ye+1)1+' p ^ (1 - y)1+'-p, therefore 1 p-ε p-ε ^ Ilf^.w(0,1) , (1 - ye+1)p-'-1 ye(p—' —1) + 1 1 p- dy dt (1 - ye+1)p-'-1 ув(р-'-1) + 1 y 1p1 C< pp ((в + 1)1-2) p . Since for all 1 а а / (1 - ув+1)1+'-р dy=aim / (1 - ув+1)1+'-р dy ca™ / (1 - y)1+'-pdy. By putting f (t) = в + 1 and taking in account p—^+1< у+у < 1, we get sup 0<'< 2 1 - ye+1 = (в + 1) sup tP— 0<'< 2 1 - ye+1 < (в + 1) sup t p— 0<'< 2 i (1 - y)p-'-1dy 1 p-ε 1 / 1 \ = (в + 1) sup tp^ ( — ) p I Л1 - t)p-'dt I 0<'<p p--1/ I < (в + 1) sup t ~ sup (------< (в + 1) 0<'<2 0<'<2 \p - t / p-- t + 1/ sup tp-e . p 0<'< 2 On the other hand HH1f^Lp) (0,1) = 1Н1(в + 1)1^ (0,1) by (2.9), we conclude that (в + 1) sup EP- < C(в + 1) sup EP- 0<£< 2 0<£< 2 (я thus C ^ (2)p. The proof is complete. > Remark 5. If в = 0 in (2.10), we have Theorem 4 of [7]. A similar results hold for p = 1. Corollary 3. Let f G Li)(0,1), f G Qв, в ^ 0. Then there exists a constant C > 0, such that (1 / 1 e/(/ 0 \t (1 - ye+1) y-Д5+1 5 I - dy \ f1-5(t) dt 1 1-ε . (2.11) If C is the best constant in (2.11), then 4 C C C (в + 1)2. (2.12) Remark 6. If в = 0 in (2.12), we find Theorem 6 of [7].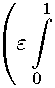
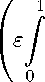
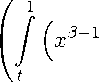
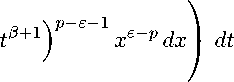
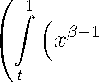
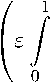
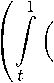
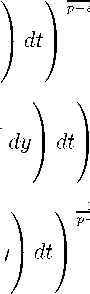
Список литературы Hardy type inequalities in classical and grand Lebesgue spaces lp), 0
- Iwaniec, T. and Sbordone, C. On the Integrability of the Jacobian Under Minimal Hypotheses, Archive for Rational Mechanics and Analysis, Springer-Verlag, 1992, vol. 119, no. 2, pp. 129-143.
- Capone, C. and Fiorenza, A. On small Lebesgue spaces, Journal of Function Spaces, 2005, vol. 3, no. 1, pp. 73-89. DOI: 10.1155/2005/192538
- Fiorenza, A. and Karadzhov, G. E. Grand and Small Lebesgue Spaces and Their Analogs, Zeitschrift fur Analysis und ihre Anwendungen, 2004, vol. 23, no. 4, pp. 657-681. DOI: 10.4171/ZAA/1215
- Samko, S. G. and Umarkhadzhiev, S. M. Local Grand Lebesgue Spaces, Vladikavkaz Math. J., 2021, vol. 23, no. 4, pp. 96-108. DOI: 10.46698/e4624-8934-5248-n
- Umarkhadzhiev, S. M. Generalization of the Notion of Grand Lebesgue Space, Russian Mathematics, 2014, vol. 58, no. 4, pp. 35-43. DOI: 10.3103/S1066369X14040057
- Umarkhadzhiev, S. M. One-Dimensional and Multidimensional Hardy Operators in Grand Lebesgue Spaces, Azerbaijan Journal of Mathematics, 2017, vol. 7, no. 2, pp. 132-152.
- Bandaliev, A. R. and Safarova, K. H. On Hardy Type Inequalities in Grand Lebesgue Spaces Lp) for 0.
- Bergh, J., Burenkov, V. and Persson, L.-E. Best Constants in Reversed Hardy's Inequalities for Quasimonotone Functions, Acta Scientiarum Mathematicarum, Szeged, 1994, vol. 59, no. 1-2, pp. 221-239.


