Helical parameters of regular -helices in proteins

Helix is one of two main types of secondary structures in proteins. Helices are usually designated as i n based on the number of residues per turn ( i ) and the number of atoms in the ring joined by the backbone hydrogen bond ( n ) [3]. Pauling and Corey first hypothesized the α-helix (3.6 13 ) and the γ-helix (5.l 17 ) structures [15]. Donohue later considered the possibility of other types of helices (2.2, 3 10 , 4.3 14 and 4.4 16 ) [3]. Low and Baybutt also suggested the possibility of the 4.4 16 -helix or π-helix [14]. The main stabilizing factor for helical structures in polypeptides is repeat hydrogen bonds between main chain carbonyl oxygen (C = O) and amide hydrogen (NH) groups with the π-helix characterized by an ( i ← i+ 4) pattern, the 3 10 - and the π-helix by repealing ( i ← i+ 3) and ( i ← i+ 5) hydrogen bonds, respectively [11].

There are several programs perform assignments of secondary structures based on three-dimensional atomic coordinates of proteins [7, 11]. Among these, DSSP (Kahsch and Sander, 1983) and STRIDE (Frishman and Argos, 1995) are the most widely used. While DSSP identifies helices based on the repeating (i←i+n ) hydrogen bonds with corresponding to n of 3, 4 and 5 for 3 10 , α- and π-helices, respectively [11], the STRIDE uses both of hydrogen bonds and main chain dihedral angles to define secondary structures. DSSP program identified only 9 unique π-helices from the database of more than 6000 of proteins [19]. Fodje and Karadaghi defined 116 π-helices using their home made program, SECSTR, from the database of 932 high-resolution three-dimensional structures of proteins [8].

These different results can be explained by the following two reasons: 1) Number of solved 3D structures were insufficient by this time 2) Programs to assign of secondary structures are using different methods.

We studied helical parameters of protein helices with HELFIT program and compared with the parameters of canonical π -helices.

Materials and Methods

Composition of Database

The 16 May 2016 culled PDB data set, containing 2969 protein chains with less than 20% sequence identity and 1.6 Å resolution ( R -value ≤ 0.25), was used in this analysis.

DSSP program

DSSP performs secondary structure assignments by the bonding energy Е ≤ -0.5 kcal/mоl between C=O of residue i and N–H residue n ( i ← i+n ). The optimal hydrogen bonding energy for mainchain-mainchain N—H···O hydrogen bonds Е m < -3 kcal/mol. Hydrogen bond energy depends on both electrostatic interaction N—H···O of atoms and of hydrogen bonds angle θ [11].

They calculate the electrostatic interaction energy between two hydrogen bonding groups by placing partial charges on the C, O (+ q 1 , - q 1 ) and N, H (- q 2 , + q 2 ) atoms.

E=qq |1( ON)+1( CH)-1 ( OH) + 1( CN) I-f

12 V r r r r )

E interaction potential energy (kcal/mol), q 1 = 0.42 e and q 2 = 0.20 e , e is elementary charge (| e | = 1.6·10^-19C), r is distance between two atoms (Å), the dimensional factor f = 332 kcal/ e ²mol [11].

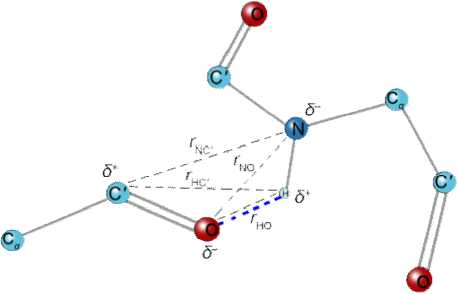
Fig. 1 . Distances used to calculate hydrogen bond energy the Coulomb interaction.

STRIDE program

STRIDE program is designed for protein secondary structure assignment from three-dimensional atomic coordinates based on the combined use of hydrogen bond energy and statistically derived backbone torsional angle information [7]. The hydrogen bond energy E hb is calculated using the empirical energy function derived from the analysis of experimental data on hydrogen bond geometries in crystal structures of amino acids in polypeptide chains;

Ehb = Er + Et + Eθ where, Er is the distance dependence of the hydrogen bond, and Et and Eθ describe its directional properties.

CD

E r r ^{8 +} r⁶

where С = -3 Е m r⁸ m kcal Å⁸/mol, D = -4 Е m r⁶ m kcal Å⁶/mol, r is the distance between the donor and acceptor atoms participating in the hydrogen bond (fig. 1), and E m and r m are the optimal hydrogen bond energy and length, respectively [7]. For mainchain-mainchain hydrogen bonds N—H···O, E m = -2.8 kcal/mol and r m = 3.0 Å [11]. The angular terms E t and E θ have the following forms:

E θ = cos² θ and

0 <  t , <  90 ° 90 ° <  t , <  110 ° t , >  110 °

(0.9 + 0.1sin 2 t ) cos 1 ₀,

E„ = 1 K ( K - cos ² t ) ³ cos t _n, θ    12          0

10, where, K1 = 0.9/cos6110o, K2 = cos2110o and CαC'NO atoms situated in flat because ti is of rOH in flat (from O atom to H atom drawn radius vector) mapping C' - O of bond from directional deviation angle, t0 is between rOH radius vector and flat angle (fig. 2).

SECSTR program

SECSTR is a new addition to the DSSP program that is dedicated to identifying π-helices, which were seldom assigned by older versions of DSSP and STRIDE [8]. The secondary structure assignment methods based on hydrogen bond assignments (DSSP, STRIDE, and SECSTR) produced nearly identical assignments, with more than to 90% [20].

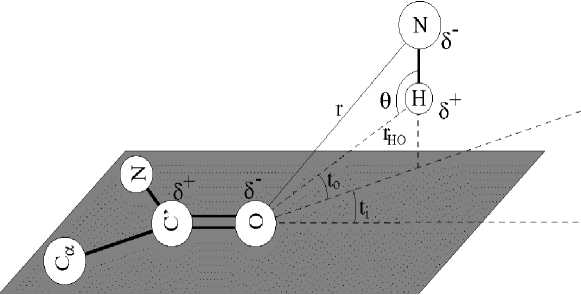
Fig. 2 . An illustration of main-chain hydrogen bond geometry as adapted from Boobbyer et al .

HELFIT program

HELFIT is a continuous helical five parameters described with least squares method. Therefore

• 1.    the direction vector of the helix axis ( a x , a y , a z )

• 2.    the radius of the helix r

• 3.    radius of the helix and its +/- error r and ±Δ r

• 4.    the pitch of the helix P

• 5.    number of residue per turn n

This program described the helical parameters with high accuracy for the analysis least four of data points three-dimensional coordinate and these points are coordinate of C α atoms of amino acids of helix type secondary structure in polypeptide chain. Above the helical some parameters specification displacement of the helix axis along per turn or pitch P , it also calculates a parameter p = rmsd / ( N -1)^1/2, where rmsd is the root mean square distance from the best-fit helix to data points and N is the number of data points [6].

Discussion and Results

The α-helix is considered to be the most abundant form of secondary structure, accounting for about 31% of amino acid secondary structure states, while the 310-helix accounts for about 4% [1, 2]. The π-helix, however, appears to be extremely rare. The rarity of the π-helix has been attributed to its instability due to the following properties: (1) the dihedral angles φ and ψ are unfavorable, lying at the very edge of an allowed minimum energy region of the Ramachandran plot [17]; (2) the larger radius of the π-helix means that main chain atoms are no longer in van der Waals contact along the helix axis, resulting in a hole too small for a water molecules to fill [14]; (3) a large entropic cost is required to form a helix in which five residues need to be aligned to permit the (i←i+5) hydrogen bond [16]. A few researchers have, however, found π-helices to be formed during molecular dynamics simulations of peptides [12] with some reports of a transition from α-helix to π-helix structure [4]. This suggests that the π-helix is not as unstable as previously believed.

We identified 27, 22 and 340 π-helices from 2901 proteins by DSSP, STRIDE and SECSTR respectively. All π-helices are divided into two types, regular and irregular, with p -value: p ≤ 0.10 Å regular and p >  0.10 Å irregular. In order to compare protein π-helices with the canonical π-helices the only parameters of regular π-helices’ are used for the further analysis.

Table 1

Helical parameters of 7 regular π-helices in proteins

Length P (Å) n Δzb (Å) r (Å) Vc (Å3)a p (Å) Average 7.71 5.13 4.41 1.16 2.76 27.76 0.07 Standard deviation 0.76 0.10 0.09 0.03 0.04 0.77 0.03 Minimum 7.00 5.01 4.25 1.11 2.68 26.76 0.02 Maximum 9.00 5.30 4.53 1.19 2.81 29.20 0.10 Canonical - 5.16 4.40 1.15 2.68 25.90 - a Voronoi volume (Vc=π·r2·Δz), b Helix rise per residue Δz=P/n

Helical parameters of π-helices identified by DSSP program

Total 27 (20 irregular π-helices) π-helices are identified from 2901 proteins by DSSP program. Helix length, helical parameters, and p -values of π-helices in protein are determined with the HELFIT program (Table 1).

Helix radius of real π-helices is larger than the radius of canonical π-helix, also Voronoi volume of real π-helices is larger than canonical π-helix. The other helix parameters are close to the parameters of canonical p-helix. Average length is 7.71 and length is range of 7-9 residues.

Helical parameters of π-helices identified by STRIDE program

π-helices (22) are identified the high resolution 3D structures of proteins by DSSP program. Helical parameters, and p-values of π-helices in protein are determined with the HELFIT program and Voronoi volume ( V^a ) and helix rise per residue (Δ z ) are calculated of π-helices (Table 2).

Table 2

Helical parameters of 6 regular π-helices in proteins

	Length	P (Å)	n	Δ zb (Å)	r (Å)	V c (Å3) a	p (Å)
Average	7	5.10	4.46	1.14	2.78	27.65	0.07
Standard deviation	0	0.06	0.06	0.02	0.03	0.36	0.04
Minimum	7	4.99	4.40	1.10	2.74	27.33	0.03
Maximum	7	5.14	4.54	1.17	2.81	28.39	0.14
Canonical	-	5.16	4.40	1.15	2.68	25.90

Length of all real π-helices is same and helix radius of real π-helices is larger than the radius of canonical π-helix. Real values of P , r are close to the parameters of canonical π-helix.

Helical parameters of π-helices identified by SECSTR program

340 π-helices (264 are irregular helices) are identified the high resolution 3D structures of proteins by SECSTR program. Helical parameters of π-helices in protein are determined with the HELFIT program and Voronoi volume ( V^a ) and helix rise per residue (Δ z ) are calculated of π-helices (Table 3).

Table 3

Helical parameters of 76 regular π-helices in proteins

	Length	P (Å)	n	Δ zb (Å)	r (Å)	V c (Å3) a	p (Å)
Average	7.42	5.18	4.40	1.18	2.75	28.10	0.08
Standard deviation	1.16	0.12	0.21	0.09	0.06	1.98	0.02
Minimum	5.00	4.82	2.99	1.03	2.58	23.93	0.03
Maximum	12.00	5.51	5.07	1.84	2.88	42.20	0.10
Canonical	-	5.16	4.40	1.15	2.68	25.90	-

Real values of P , Δ z , r , and V c , more than those of canonical helix and value of same that of canonical π-helix.

Conclusion

• •    2901 3D structures of high resolution protein structures were downloaded from Protein Data Bank (PDB) and there are 389 π-helices. In average, every protein contains 0.13 π-helices.

• •    All π-helices are divided into two groups, regular and irregular. There are 89 π-helices are regular among the total of 389 π-helices, 4.37%. Helix parameters of all regular π-helices are used for futher analysis.

• •    Radii of all π-helices are larger than that of canonical π-helices and all the helical parameters are comparable with those of canonical helices.