High Performance Scheduling in Parallel Heterogeneous Multiprocessor Systems Using Evolutionary Algorithms

Published Online October 2013 in MECS

In multiple processing, multiple processors work together to implement a program. The major application of these systems is for problem solving in modeling and engineering sciences (e.g. Applied Physics, Nuclear Physics, Geology and Seismology, Mechanical Engineering, Electrical Engineering, Mathematics etc.). Today, not only scientific problems solving requires parallel processing, but also some commercial applications require fast computers. Many of these applications require the processing of large volumes of complex information. Some of these programs include huge databases, data mining operations, oil exploration, medical imaging and diagnosis etc[19 - 22].

In computer networking, load balancing is a technique to spread work between two or more computers, network links, CPUs, hard drives, or other resources, in order to get optimal resource utilization, throughput, or response time. Using multiple components with load balancing, instead of a single component, may increase reliability through redundancy. Load balancing attempts to maximize system utilization by keeping all processors busy[16-20].

Static Load-Balancing In this method, the performance of the nodes is determined at the beginning of execution. Then depending upon their performance the workload is distributed in the start by the master node. The slave processors calculate their allocated work and submit their result to the master. A task is always executed on the node to which it is assigned that is static load balancing methods are non-preemptive. A general disadvantage of all static schemes is that the final selection of a host for process allocation is made when the process is created and cannot be changed during process execution to make changes in the system load[1]. Major load balancing algorithms are Round Robin[11] and Randomized Algorithms[12], Central Manager [13]Algorithm and Threshold[13, 14] Algorithm.

Dynamic Load Balancing It differs from static algorithms in that the workload is distributed among the nodes at runtime. The master assigns new processes to the slaves based on the new information collected[4, 15]. Unlike static algorithms, dynamic algorithms allocate processes dynamically when one of the processors becomes under loaded. Instead, they are uffered in the queue on the main host and allocated dynamically upon requests from remote hosts[1]. This method is consisted of Central Queue Algorithm and Local Queue Algorithm[16-18].

Load balancing algorithms work on the principle that in which situation workload is assigned, during compile time or at runtime. Comparison shows that static load balancing algorithms are more stable compare to dynamic. It is also ease to predict the behavior of static, but at the same time, dynamic distributed algorithms are always considered better than static algorithms[1, 1618].

The allocation sequence of tasks in a heterogeneous multi-processor system has direct impact on the utilization and response times. Therefore, we use genetic algorithm to determine the task’s optimal sequence for allocate to processors. In this paper, we introduce a method based on genetic algorithms for scheduling and laod balancing in parallel heterogeneous multi-processor systems. A Genetic Algorithm (GA) approach is proposed to handle the problem of parallel system task scheduling. A GA starts with generation of an individual, which is encoded as strings known as chromosomes. A chromosome corresponds to a solution to the problem. A fitness function is used to evaluate the fitness of each individual. In general, GAs consist of selection, crossover and mutation operations based on some key parameters such as fitness function, crossover probability, and mutation probability.

Results of the simulations indicate Genetic Algorithm reduce total response time in comparison with LPT, SPT and FIFO. In addition, the system utilization increase when we using Genetic Algorithm for Scheduling in parallel heterogeneous multiprocessor systems.

This study is divided into the following sections: In section 2 an overview of the problem is given along with brief description of the solution methodology. Section 3 description an overview of Genetic Algorithm. The proposed method is described in Section 4. Results of the study are analyzed in Section 5. Finally, Section 6 presents the conclusions.

• II.    Problem Definition

Parallel multi-processor systems can be homogeneous or heterogeneous: Heterogeneous means that the processors have different computing speeds and capacities. Homogeneous means that all processors have equal computing speeds and capacity [4,5,6,13].

Tasks can be independent or dependent. An independent task means that the tasks, for running, do not need to run other tasks and these tasks can be executed at any time without knowledge of the information of other tasks. On the other hand, a dependent task means that each task may require the information of other tasks for execution. For run a task should be executed other tasks.

The multiprocessor computing environment consists of a set of m heterogeneous processor:

P = {pi: i =1, 2, 3^m}                           (1)

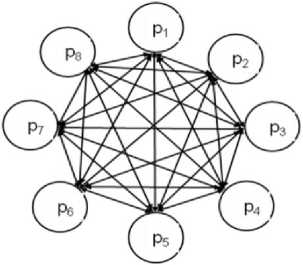
Fig. 1: A fully connected parallel processor[4]

They are fully connected with each other via identical links. Figure 1 shows a fully connected eight parallel system with identical link[4,11].

P indicates the numbers of heterogeneous processors that can be to m of exist heterogeneous processors. Processors are heterogeneous, therefore in heterogeneous environments, every processor works in different speeds and processing capabilities. Assume processor p1 is faster than p2, p3 and so on. Likewise, processor p2 is faster than p3, p4 and so on. (i.e., the order of speed and processing capabilities can be expressed as p1>p2> p3 > p4 > p5 > p6 > p7>p8) [4, 10].

According to the above description, table 1 shows an example of this problem. For example there are five tasks and two heterogeneous processors, Because processors are heterogeneous, each task has different run times on different processor.

Table 1: Shows a task execution matrix on different processors

Tasks	Tasks1	Tasks2	Tasks3	Tasks4	Tasks5
P1(Run T ime)	4	1	3	2	3
P2(Run T ime)	6	2	5	4	4

According to the example, assume tasks T1, T2, T3, T4, T5 be scheduled, respectively. Hence, scheduling is according to Figure 2. T1 first enter to processor 1. According to table 1, T1 run time in processor 1 is equal to 4. Then, T2 enter to processor 2. According to table 1, T2 run time in processor 2 is equal to 2, and on.

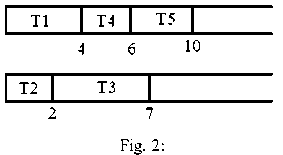
Assume tasks T3, T5, T4, T2, T1 be scheduled, respectively. Hence, scheduling is according to Figure 3. T3 first enter to processor 1. According to table 1, T1 run time in processor 1 is equal to 3. Then, T5 enter to processor 2. According to table 1, T5 run time in processor 2 is equal to 4, and on.

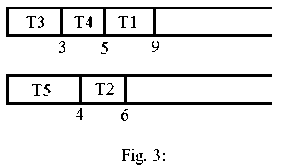
The second scheduling is optimized, compared to the first scheduling the reason is that the response time in figure 3 is 9 and response time in figure 2 is 10, on other hand, load balancing in both is same. So second scheduling order is optimal.

How to respectively Entry (scheduling) of tasks to processors that maximum utilization and also minimizes the total execution time in this sytems is NP-Complete problem.

Therefore, in this paper, we use GA for load balancing and minimizing total execution time in parallel multi-processor systems. There we assume Static Load-Balancing in this systems.

• III.    Genetic Algorithms

In the computer science field of artificial intelligence, a genetic algorithm (GA) is a search heuristic that mimics the process of natural evolution. This heuristic is routinely used to generate useful solutions to optimization and search problems. Genetic algorithms belong to the larger class of evolutionary algorithms (EA), which generate solutions to optimization problems using techniques inspired by natural evolution, such as inheritance, mutation, selection, and crossover[14].

In a genetic algorithm, a population of strings (called chromosomes or the genotype of the genome), which encode candidate solutions (called individuals, creatures, or phenotypes) to an optimization problem, evolves toward better solutions. Traditionally, solutions are represented in binary as strings of 0s and 1s, but other encodings are also possible. The evolution usually starts from a population of randomly generated individuals and happens in generations. In each generation, the fitness of every individual in the population is evaluated, multiple individuals are stochastically selected from the current population (based on their fitness), and modified (recombined and possibly randomly mutated) to form a new population. The new population is then used in the next iteration of the algorithm. Commonly, the algorithm terminates when either a maximum number of generations has been produced, or a satisfactory fitness level has been reached for the population. If the algorithm has terminated due to a maximum number of generations, a satisfactory solution may or may not have been reached.

Genetic algorithms find application in bioinformatics, phylogenetics, computational science, engineering, economics, chemistry, manufacturing, mathematics, physics and other fields.

The fitness function is defined over the genetic representation and measures the quality of the represented solution. The fitness function is always problem dependent. For instance, in the knapsack problem one wants to maximize the total value of objects that can be put in a knapsack of some fixed capacity. A representation of a solution might be an array of bits, where each bit represents a different object, and the value of the bit (0 or 1) represents whether or not the object is in the knapsack. Not every such representation is valid, as the size of objects may exceed the capacity of the knapsack. The fitness of the solution is the sum of values of all objects in the knapsack if the representation is valid, or 0 otherwise. In some problems, it is hard or even impossible to define the fitness expression; in these cases, interactive genetic algorithms are used.

Once the genetic representation and the fitness function are defined, a GA proceeds to initialize a population of solutions (usually randomly) and then to improve it through repetitive application of the mutation, crossover, inversion and selection operators.

In genetic algorithms, crossover is a genetic operator used to vary the programming of a chromosome or chromosomes from one generation to the next. It is analogous to reproduction and biological crossover, upon which genetic algorithms are based. Cross over is a process of taking more than one parent solutions and producing a child solution from them. There are methods for selection of the chromosomes.

In genetic algorithms, mutation is a genetic operator used to maintain genetic diversity from one generation of a population of algorithm chromosomes to the next. It is analogous to biological mutation. Mutation alters one or more gene values in a chromosome from its initial state. In mutation, the solution may change entirely from the previous solution. Hence GA can come to better solution by using mutation. Mutation occurs during evolution according to a user-definable mutation probability. This probability should be set low. If it is set too high, the search will turn into a primitive random search[14]. GA using operator selection, combination and mutation provide the optimal solution that is not possible with other methods. Figure 4 shown genetic algorithm chart.

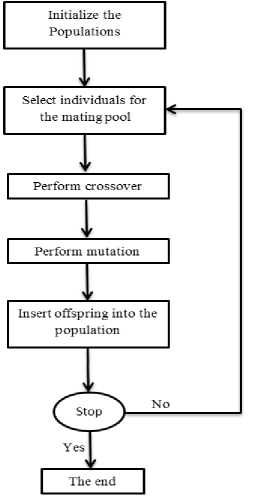
Fig. 4: Genetic Algorithm chart

• IV.    Scheduling and Load Balancing using Genetic Algorithms in Parallel Multi-Processor Systems

• 4.1    Encoding

• 4.2    Generate the Initial Population

• 4.3    Fitness Function

The purpose of this study is to find a sequence of tasks for load balancing and minimizing total execution time in parallel multi-processor systems. Thus, each chromosome is sequence variety of tasks. Each task is considered as a gene. Therefore, the best way to encode chromosomes is permutations encoding. To explain how chromosomes are encoded, consider that there are 8 tasks, Ti represents the tasks. figure 5 shows two encoded chromosomes.

Ch 1	T1	T4	Is	T2	Т7	Тз	Тб	Т5
Ch 2	Тб	T1	Т?	Тз	Т5	Т8	Тз	Т4

Fig. 5: two of chromosome encoded

To start, GA should generate an initial random population for entry into the first generation. For this, a random generator function of chromosomes must be employed[4]. In order to create an initial population, we need Information on the number of processors, number of tasks and the size of the population. Random chromosomes generate the initial population.

The important part of GA is the fitness function. The fitness function is defined over the genetic representation, and measures quality of the chromosomes. The fitness function is always dependent on the problem. In this paper, the fitness function separates evaluation into two parts: load balancing(system utilization) and total response time.

The fitness function is calculated according to the (2) equation:

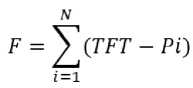
TFT is total response time obtained from the chromosome. Pi is Processor i and N is complete number of processors. Lesser value of the above equation corresponds to a better fitness value for the chromosome.

selected according to their fitness value. Once fitness values have been evaluated for all chromosomes, we can select good chromosomes through rotating roulette wheel strategy. This operator generate next generationby selecting best chromosomes from parents and offspring[4].

• 4.5    Crossover Operator

• 4.6    Mutation Operator

Crossover operator randomly selects two parent chromosomes (chromosomes with higher values have more chance to be selected) and randomly chooses their crossover points, and mates them to produce two child (offspring) chromosomes[4]. We consider one point crossover in here, In one point crossover, the segments to the right of the crossover points are exchanged to form two offspring as shown in figure 6.

parent 1	Т1	Тз	Т4	Т2	Ts	I	Тб	Т7
parent 2	Т5	Тз	Т1	Т4	Т7	Т8	Тб	Т2
Child	Т1	Тз	Т4	Т5	Т7	Та	Тб	Т2

Fig. 6: One point crossover

A mutation operation works by randomly selecting two tasks and swapping them. Firstly, it randomly selects a processor, and then randomly selects a task on that processor[4]. This task is the first task of the pair to be swapped. Secondly, it randomly selects a second processor (it may be the same as the first), and randomly selects a task. If the two selected tasks are the same task the search continues on. If the two tasks are different then they are swapped over (provided that the precedence relations must satisfy). figure 7.

befor	Т1	Т4	Та	Т2	Т7	Тз	Тб	Т5
ofter	Т1	Т7	Та	Т2	Т4	Тз	Тб	Т5

Fig. 7: Mutation operator

• V. Evaluation and Simulation Results

• 4.4 Selection Operator

In this section, we present and discuss the experimental results of the proposed scheme. All simulations were performed using MATLAB software. We evaluated the performance of our proposed scheme in comparison with LPT (Largest Processing Time), SPT (Shortest Processing Time), and FIFO algorithms in a Parallel multi-processor system.

The parameters of the considered GA are as table 2:

The design of the fitness function is the basic of selection operation, so how to design the fitness function will directly affect the performance of genetic algorithm. GAs uses selection operator to select the superior and eliminate the inferior. The individual are

Table 2:

Number of generations	40
Crossover probability	50%
Mutation probability	20%
Chromosomes that enter the next generation unchanged	30%
Number of GA iterations	200

We abtained results from applying Genetic algorithm compare with abtained results from applying LPT, SPT and FIFO algorithms. Our experiments are in two part:

• •    When the number of tasks is 50

• •    When the number of tasks is 500

When the number of tasks are 50, figure 8 and figure 12 shows total response time by applying LPT, SPT, FIFO and Genetic Algorithm for tasks scheduling on parallel multi-processor systems. abtained results in figure 8 and 12 shown GA have total response time less than LPT, SPT and FIFO. Also figure 9 and figure 14 shown system utilization in GA is better than LPT, SPT and FIFO when number of tasks are 50. This is mean the GA's system utilization is better, also it has minimum response time. So when number of tasks are 50 the total response time and system utilization for GA is better at comaper with LPT, SPT and FIFO.

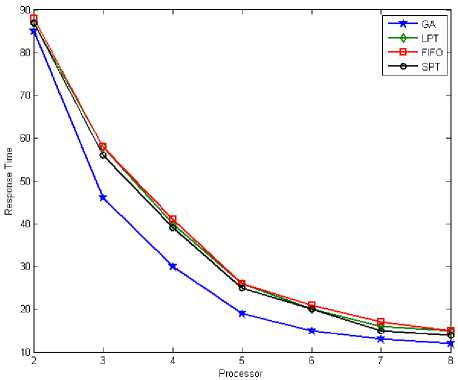
Fig. 8: Total Response Time (Tasks = 50)

processors.

When the number of tasks are 500, figure 10 and figure 13 shows total response time by applying LPT, SPT, FIFO and Genetic Algorithm for tasks scheduling on parallel multi-processor systems.

Genetic Algorithm in addition to reducing the total response time, provides good utilization compared to the LPT, SPT and FIFO.

Abtained results in figure 10 and figure 13 shown GA have total response time less than LPT, SPT and FIFO when the number of tasks are 500. Also figure 11 and figure 15 shown system utilization when number of tasks are 500. GA's system utilization is better, also it has minimum response time compare with LPT, SPT and FIFO. So when number of tasks are 500 the total response time and system utilization for GA is better than LPT, SPT and FIFO.

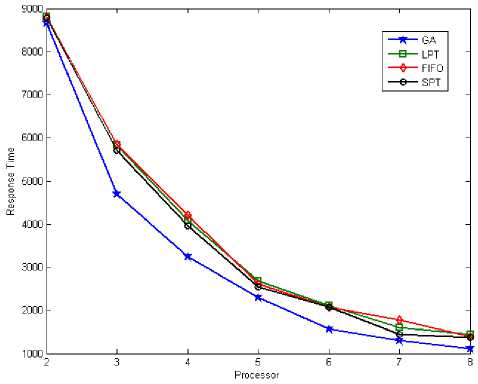
Fig. 10: Total Response Time (Tasks = 500)

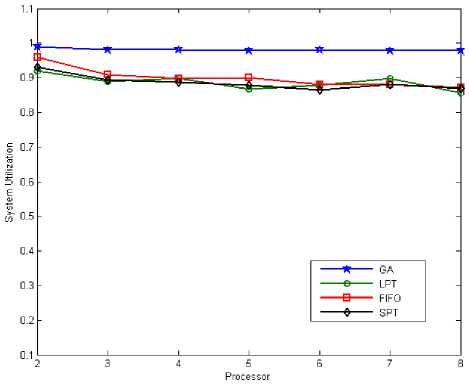
Fig. 9: System Utilization (Tasks = 50)

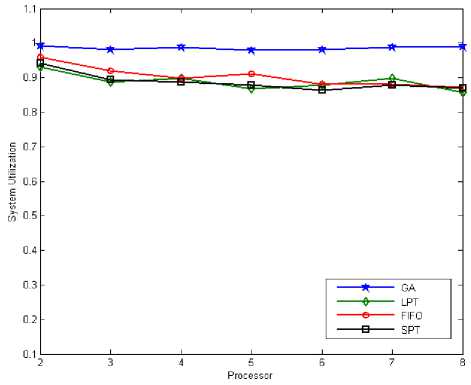
Fig. 11: System Utilization (Tasks = 500)

The vertical axis represents the total response time and the horizontal axis represents the number of

Genetic Algorithm in addition to reducing the total response time, provides good utilization compared to the LPT, SPT and FIFO in both state.

Obtained results in large and small scales indicate that Genetic Algorithm for scheduling and laod balancing can provide similar results in different scales, and proves therobustness of the Genetic algorithm in different scales.

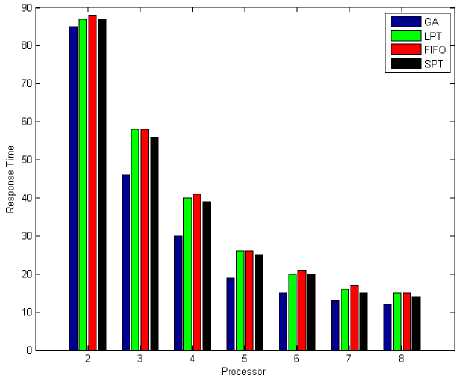
Fig. 12: Total Response Time (Tasks = 50)

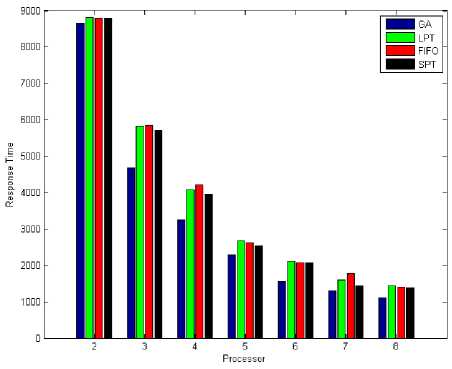
Fig. 13: Total Response Time (Tasks = 500)

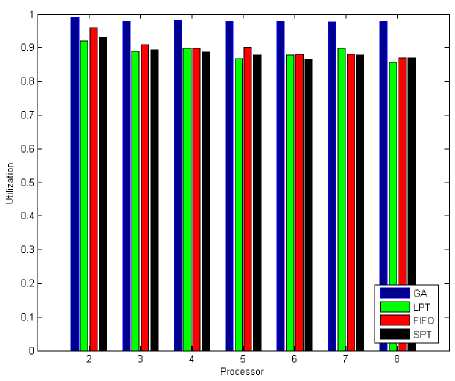
Fig. 14: System Utilization (Tasks = 50)

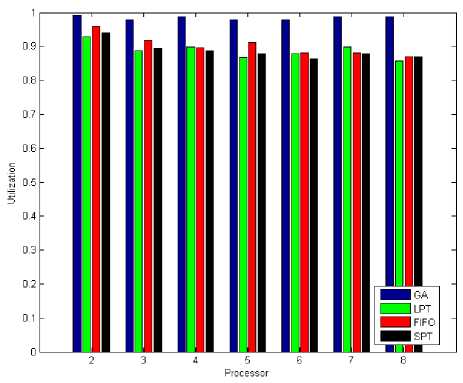
Fig. 15: System Utilization (Tasks = 500)

• VI. Conclusion

In this study, we proposed the Genetic Algorithm (GA) for tasks scheduling and load balancing in heterogeneous parallel multiprocessor systems that reduce total response time and increase system utilization. The proposed method found a better solution for assigning tasks to the heterogeneous parallel multiprocessor system. The method proposed in this article was compared with LPT, SPT and FIFO algorithms. The results of simulations indicate that our method is better at compared with the other method. In addition, the obtained results are based on a limited number of reproduction and genetic simple operators. Certainly, gain the better results using of efficiently operators.