Химические потенциалы тетрагонального феррита и его равновесие с γ-фазой в сталях

Распад переохлажденного аустенита дает различные структуры в зависимости от температуры и скорости превращения. Между ступенью ферритно-перлитного и мартенситного превращения аустенита расположена ступень промежуточного или бейнитного превращения [1], которая в последнее время опять привлекла внимание материаловедов благодаря разработке прекрасных сталей с бескарбидным бейнитом [1, 2]. Структура верхнего бейнита состоит из относительно крупных реек или пластин феррита, чередующихся с рейками карбида Fe 3 C. На границах реек и пакетов проявляются тонкие прослойки остаточного аустенита. Выделения Fe 3 C или ε-карбида в нижнем бейните расположены под углами 60°–70° к оси реек. Вероятно, они возникают после завершения роста пакета. Несомненно, что в условиях непрерывного охлаждения, а тем более в ходе изотермической выдержки, существует период времени, в течение которого аустенит и бей-нитный феррит могут обмениваться атомами углерода. При этом аустенит обогащается углеродом, бейнит, напротив, обедняется, а часть углерода выделяется в виде карбида, в большей степени для верхнего, в меньшей – для нижнего бейнита. Однако если сталь содержит легирующие элементы (Si, Al) [1, 2], действие которых проявляется не только в уменьшении коэффициента диффузии углерода, но и в устойчивости карбидов, то в условиях непрерывного охлаждения или изотермической закалки возникает структура бескарбидного бейнита, включающая также остаточный аустенит и мартенсит последующего охлаждения. Изотермически закаленная сталь с бес-карбидным бейнитом обладает [2, 3] высоким уровнем конструкционной прочности, тогда как появление частиц карбида приводит к резкому снижению сопротивления удару. Таким образом, в сталях с бескарбидным бейнитом возникает равновесие феррит-аустенит, которое можно изучать при низких температурах.

Бхадешия одним из первых обратил внимание [4–6] на отмеченные свойства кремнистых сталей. Им были разработаны новые высокоуглеродистые Mn-Si-cтали, в которых при изотермической закалке возникают тонкие (до 20 нм) пластины или рейки бейнитного феррита и сохраняется остаточный аустенит, который при пластической деформации превращается в мартенсит, что обеспечивает прекрасное сочетание пластичности и прочности.

Удивительным явилось то обстоятельство, что бейнит в этих сталях имеет тетрагональную кристаллическую решетку, что ранее не наблюдалось, вероятно, вследствие выделения карбидов. Факт тетрагональности подтвержден прямыми экспериментами в работах [7, 8]. Бхадешия представил [6] диаграмму равновесия тетрагонального феррита (α’) и аустенита (γ) при различных температурах. Оказалось, что равновесная концентрация углерода в феррите увеличилась при этом многократно. Однако проведенный автором расчет изменения энергии растворения углеро-

Мирзаев Д.А., Мирзоев А.А., Булдашев И.В., Окишев К.Ю.

да при переходе от кубического к тетрагональному ферриту имеет ряд недостатков. В кубическом феррите углерод равномерно распределен между тремя подрешетками октапор (х-, у-, z-типа). Бхадешия, как обычно при первопринципных расчетах, использовал периодические граничные условия [6], а в суперячейку помещал единственный атом углерода. Такие условия «транслируют» данный атом всегда в подрешетку одного вида. Поэтому фактически Бхадешия рассчитал энергию растворения углерода в кубическом феррите с содержанием углерода 1,3 мас. %. В естественных условиях такой кубический феррит не стабилен; подобно мартенситу он должен приобрести тетрагональную решетку, вытянутую вдоль оси z с отношением c / a = 1,059. В реальности, чтобы создать такой кубический феррит, необходимо к тетрагональному кристаллу приложить сжимающее вдоль оси z и растягивающие вдоль осей х и у напряжения, которые увеличат полную энергию системы за счет дополнительного вклада упругой энергии. Эта добавочная энергия приводит к увеличению энергии растворения углерода в кубической ферритной фазе и, возможно, к завышенному результату для разности энергий растворения. Второй недостаток подхода состоит в том, что автор не описывает процедуру расчета фазовой диаграммы тетрагональный феррит/аустенит, для которого необходим учет изменения энтропии углерода при переходе от неупорядоченного распределения к упорядоченному в z-подрешетке для тетрагонального феррита. Поскольку этот очень важный факт не отмечен, то, скорее всего, автор принимал энтропию в обоих состояниях одинаковой. Полученная Бхадешия фазовая диаграмма чрезвычайно важна для понимания направлений развития данного класса сталей. Однако точный расчет такой диаграммы возможен только при знании химических потенциалов углерода и железа применительно хотя бы к углеродистым сталям. В связи с этим данная статья посвящена анализу химических потенциалов тетрагонального феррита и строгому расчету диаграммы равновесия у ^ a .

Химические потенциалы компонентов кубического феррита

Теория идеальных растворов внедрения, в том числе углерода в железе, была разработана в работах [9–10]. На ее основе получено выражение для термодинамической вероятности W и энтропии S распределения n атомов углерода по βN октаэдрическим порам решетки железа

S = k B ln W = - k_B

n _c ln — n C + P N ln ^ N—— I C I N - n c         e N ^J

,

где nC и N - количество растворенных атомов углерода и атомов растворителя, а в — число октаэдрических пор, приходящихся на атом железа ( в = 1 для ГЦК и в = 3 для ОЦК решетки железа). Энтропийные вклады в молярные химические потенциалы компонентов составят:

ц ^ S ) = RT ln

x a

3 - 4 x g

; Ц ( s ) = RT in

x !                3 - 4 x ^g              1 - 2 x ^

---^C—; ц _Не = RT in—---C-; ц !. = RT in----^C,

1 - 2 x C ^eS )         3 ( 1 - x g ) ^Fe ⁽ S )          1 - x ^Y

где x _C и x _Fe – атомные доли углерода и железа в α- или γ-растворах.

Если за стандартное состояние углерода в растворе принять графит, то растворение графита в железе формально можно разделить на ряд этапов: 1) диссоциация графита на отдельные атомы С; 2) помещение атомов С в октаэдрические поры железа, при котором возникает потенциальная энергия Е связи С-Fe, кинетическая энергия и энтропия колебаний атомов углерода; 3) включение взаимодействия Δ U атомов углерода друг с другом в объеме, содержащем N атомов железа, которое изменит и вибрационную энтропию ΔS^*. Поскольку два первых вклада пропорциональ-

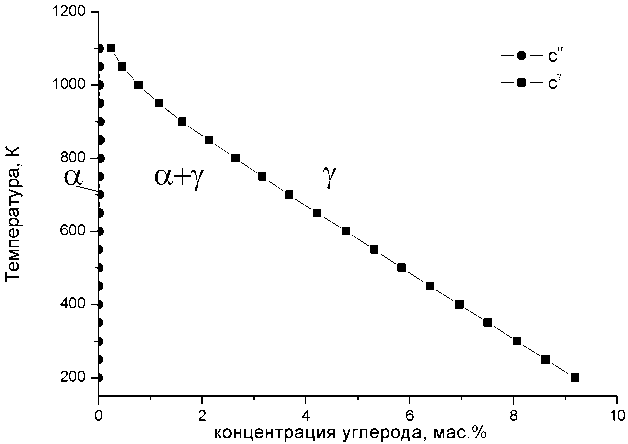
Рис. 1. Результаты расчёта диаграммы фазового равновесия кубический феррит/аустенит. Содержание углерода пересчитано от атомных долей в мас.%

Физика ны числу атомов С, то они войдут в химический потенциал атомов углерода. Обозначим их сум- му как фС. Третье слагаемое при точном расчете имеет вид в

^X C

I в ( 1 - X С ) у

у

( a U - T A S * ) , поэтому

после дифференцирования оно войдет в выражения для химических потенциалов обоих компонентов:

г

P Fe = 0 G Fe ^{+ в}

^x C

V в ( 1 - X C ) у

у

( a U - T A S * ) + в-RT in

^ (Y ^- X Clz X c • в (1 - x C ) ;

(3а)

0 гр 0

^p c = ^G C ^{+ ф} С ^-

• 2    , ^X C _x ( A U - T A S *) + RT in----- ^X C-----,

( 1 ^{- X} C Г                   ^{в (1 - X} c ) ^{- X} C

(3б)

где ⁰ G _Fe – свободная энергия чистого α- или γ- железа, а ⁰ G _C ^гр – свободная энергия графита.

Конкретно в данном исследовании были использованы термодинамические функции альфаи гамма-растворов (Дж/моль), взятые из работ Агрена [11], который опирался на исследование Харвига [12]:

y Y      Y pY = 0 gгр + 46115 -19,178 • t + rt • in---C_ + 2 C (21079 +11,555 • T);

C C                                1 - 2 x ^Y    1 - x C ⁽                  )

(4а)

pY_e = ⁰ G Y + RT in¹^ Fe Fe

• ^{1    - X} c

( V Y x _C

1 -X Y

V ^{1 X} с У

( 21079 + 11,555 • T ) ;

(4б)

xа ра = 0 GГР +108299 - 39,603 • T + RT • in---^;

C C                          3-4x“

а ра=0 Ga+з rt in^—C..

3 ( 1 - х а )

(4в)

(4г)

Сравнивая эти выражения с общими формулами (3) для регулярных растворов внедрения, можно заключить, что по Агрену энергия взаимодействия атомов углерода в ОЦК (α)-неупорядоченном растворе близка к нулю. В то же время в гамма-фазе между ними наблюдается отталкивание. Приравняв химические потенциалы углерода и железа для феррита и аустенита, а именно p" Y = P c и P a e = P a e , получим уравнения равновесия альфа- и гамма-растворов:

(⁰ G Y e - ⁰ G a e ) + RT in 1-25.

^{1 - X} c

( V Y x _C

1 — X^У

V ^{1 X} С у

a

( 21079 + 11,555 • T ) - 3 RT in—---- C = 0;

3 ( 1 - х а )

(5а)

62184 - 20,425 • T + RT • in

V

х ^а 1 - 2 x Y "

3 - 4 х ^а x ^y _у

X У

2 C ( 21079 + 11,555 • T ) = 0.

1 - x Y

(5б)

Численные значения разности свободных энергий γ- и α-фаз были рассчитаны с помощью метода, развитого Агреном [11]. Вычисление корней системы уравнений (5а) и (5б) для различных значений температуры было выполнено численно в программном пакете Маthcad . Результаты расчетов представлены на рис. 1 в виде диаграммы α-γ равновесия. Полученные данные хорошо согласуются с реально существующим участком α-γ равновесия диаграммы железо-графит [10].

Химические потенциалы компонентов тетрагонального а -феррита

За основу построения химических потенциалов была принята теория упорядочения атомов углерода в z -подрешетке внедрения мартенсита сплавов Fe-C [13]. Оно обусловлено деформационным взаимодействием атомов углерода, расположенных в октаэдрических порах с короткой диагональю октаэдра, ориентированной вдоль оси z. При этом каждый внедренный атом углерода создает поле растяжений, ориентированное вдоль этой оси. Их сумма порождает эффективное

Мирзаев Д.А., Мирзоев А.А., Химические потенциалы тетрагонального феррита Булдашев И.В., Окишев К.Ю.и его равновесие с Y -фазой в сталях напряжение, устанавливающее, подобно эффективному полю в теории магнетизма [14], упругие диполи преимущественно вдоль z. Это приводит к преимущественному заполнению атомами углерода одной (z) из трех подрешеток внедрения. Для изменения свободной энергии сплава в ходе подобного упорядочения К. Зинер [13], а затем А. Хачатурян [15] получили выражение

G ( c , T , n ) = G ( c , T ,0 ) - 3 Nc² An ² + k B Tn C [ 2 ( 1 - n ) ln ( 1 - n ) + ( 1 + 2 n ) ln ( 1 + 2 n ) ] , (6)

где n =

ⁿ C 3 ⁿ C

² 3 n C

есть параметр порядка, отражающий избыток атомов углерода в z-октаэдрических порах по сравнению с тем количеством, которое должно быть при равномерном заполнении атомами углерода пор типа z, x и y | nC = nCC = nC = nC |. Здесь N и nC - количество атомов железа и углерода со- nx ответственно; 2о - параметр деформационного взаимодействия, c = — = ——, где хс - доля N 1 - x C       C атомов углерода в растворе, T – абсолютная температура, kB – постоянная Больцмана; G(c,T,0) - свободная энергия раствора при n = 0, т. е. в неупорядоченном состоянии. Отметим, что энергия деформационного взаимодействия отрицательна, поэтому мы примем, что Л0 -положительная величина, но вынесем знак минус перед вторым слагаемым в (6). В равновесном д G (c, T ,n)

состоянии---------= 0. В результате решения получаем dn kBT (1- xC) = n

Л) x c      ln ( ^{1 +} 2 n

.

I 1 -n)

Детальный анализ устойчивости процесса упорядочения [16] показал, что указанная зависимость действительна на интервале 0,5 < n ^ 1• Значение n = 0,5 является критическим. При соот- ветствующей этому значению температуре TC :

Т С = 0,361

Л) x C k B ( 1 ^- x C )

должен проявиться переход типа порядок–беспорядок. Прохождение через эту температуру в условиях нагрева будет сопровождаться скачкообразным снижением степени порядка от 0,5 до нуля. В случае охлаждения порядок возникает также скачком.

Для упорядоченного по z состояния, предполагая что n CC = n Cy , найдем с учетом (7):

n C = n C ( 1 + 2 n ) ; n C = n C = n C ( 1 - n ) .                         (10)

Энтропия разбиения системы из n _C атомов углерода на три группы по n _C ^x , n _C ^y , n _C ^z атомов определяется термодинамической вероятностью W :

S = k_B In W = k_B In

n ^C!

I n z ! n y ! n x ! J CCC

.

Используя далее формулу Стирлинга ln N ! = N In N - N , получим выражение для энтропийного сомножителя в (6).

Перераспределение углерода, по-видимому, происходит на межфазной γ/α-границе в ходе мартенситного превращения, поскольку атом углерода в октапоре аустенита окружен симметрично тремя x -, y - и z -октапорами тетрагональной решетки. Вектор перемещения атома углерода мал во всех случаях, поэтому перераспределение атомов углерода вполне возможно даже при очень высокой, почти звуковой скорости роста. Другая ситуация складывается в случае образо-

Физика вания бейнитного феррита, когда скорость роста мала, и атомы углерода успевают перемещаться на значительные расстояния. Поэтому, если первое слагаемое в (6), связанное с коллективным деформационным взаимодействием, на наш взгляд, остается справедливым и для бейнитного феррита, то энтропийный вклад должен быть изменен. Действительно, необходимо учесть, что произвольный атом углерода в каждой подрешетке может теперь занимать любую из N октапор. Тогда

5 = k ln W =

N !            N ! N !

------------------------------:---:---------------------------:---:---------------------------:-----------------.

( N - n C ) ! n С ! ( N - n С ) ! n С ! ( N - n С ) ! n^x _C !

Вновь используя формулу Стирлинга, найдем

5 = k ln W = k ( - ( N - n C ) ln [ ( N - n C ) / N ]- ( N - n c ) ln [ ( N - n C ) / N ] -

- ( N - n C ) In [ ( N - n C ) / N ]- n C In ( n C / N ) - n C In ( n C / N ) - n C In ( n C / N ) ).

Учтем далее, что в силу равенств (10)

( x ^ ln к N J

= ln3 N + In(1 - n ) ; ln ( n C / N ) = ln nN +^ln( 1 + 2 П ) .

Тогда выражение (13) удается привести к виду:

5 = k ( n c -^( 1 ^{+ 2} П ² ) - n C ln nN - n C [ (1 + 2 П )ln(1 + 2 n ) - 2(1 - П )ln(1 - n ) ] - 3ln3]). (14)

Величина в (14), заключенная в квадратные скобки, представляет собой энтропию z-упорядочения атомов углерода, которая фигурирует в теории Зинера. Однако полная энтропия углеродной подсистемы существенно больше этого значения благодаря многократному увеличению числа позиций, доступных для размещения атомов внедрения. Что же касается энергии деформационного взаимодействия, то она должна иметь такой же вид и величину, как в теории Зи-нера–Хачатуряна. Заменив в (6) выражение для энтропии на (14), получим формулу для изменения свободной энергии A GT Ф углеродной подсистемы феррита при z-упорядочении. Молярную свободную энергию тетрагонального феррита запишем в виде Gmm‘ = AGТФ + G1(x^C‘, T), где функция G1 включает неучтенные слагаемые, необходимые, чтобы в качестве стандартных состояний выступали чистое α-железо, а для углерода – графит:

G , ( x C , T ) = ( 1 - x ? )^- G Fe + x " ( • G С р +> a ). (15)

Величина ф представляет изменение свободной энергии при переходе от стандартного состояния бесконечно разбавленного раствора углерода в α-железе к состоянию графита. Численное значение Фр“ = 95 818 - 41,92 • T Дж/моль взято из работы Агрена [11]. Для молярной свободной энергии тетрагонального феррита окончательно получаем:

G " ( x " , T , n ) = ( 1 - x ? ) ° G F * + x?' ( ° G Ср - Ф С ) - 3 N о Л,

'

(xC^T n ² + RTx g In

1 - x C

x C

1 —^ ^а к^{1 x} C

^

11+

^V (16)

+ RT (x cL ( 1 + 2 n ² ) + 1 RTx ^a [ 2 ( 1 -n ) In ( 1 - n ) + ( 1 + 2 n ) In ( 1 + 2 r ) - 3ln3 ] .

^{1 - x} C

Используем известные термодинамические формулы [10] для расчета химических потенциалов компонентов сплава

a^aV^х ' ^ G m. 0^хa^a' ^ C   ^Gm ⁺ ( ^{1   x} C )     ‘ ; M Fe  ^Gm

^{V !} d x C

'

_Y a ^{d G} m x C        '

d x CC

и найдем последние:

Мирзаев Д.А., Мирзоев А. А., Булдашев И.В., Окишев К.Ю.

'

а с = g²c^p + Ф а + RT ln

^ у ^а _x c

к

к

1 — х ^а к 1 — х _с 7

'

1 х а

+ C

³ 1 — х

к

С

- C 7

а

2( N ^ — RT ) ^с п ² +

³              1 — х а

(17а)

+ 3 RT [ 2 ( 1 — п ) ln ( 1 — п ) + ( 1 + 2 п ) ln ( 1 + 2 п ) — 3ln3 ] ;

а  0^ а

А ге = G Fe

а

RT— + -( N 0 Л ) — RT )

1 — х ^а с ³

' 2

^х с

а к 1 — хс 7

п ².

(17б)

Далее необходимо выяснить, в какой мере при п = 0 выражения (17а, б) для химических потенциалов должны перейти в формулы (4в, г) для кубического феррита. Но небольшое отклонение здесь допустимо, поскольку при выводе первых использовано приближенное выражение

(

Стирлинга. Например, сумма RT ln

функции RT ln

г 1 ^а x _C

1 — ⁴ X C к 3 7

к к

а хс

1-г ^а

^{1 х} C 7

1 х а 1

+

31 — х а 7

представляет собой 2 члена разложения

1 ха                       ха в ряд по малому параметру--C^ • Точно также RT —C^ представ-3 1 — хс                    1 — хс

ляет первый член разложения функции 3 RT ln

3 — 4 х® v 3(1—ха) v

(см. (4 г)) в ряд по малому параметру

Ха

C . Энтропийное слагаемое RT ln3 возникает и для тетрагонального, и для кубического рас-1—ха твора. В выражении (4г) оно входит в слагаемое 3RT ln

а xC

а к 3 4 х с 7

. Поскольку RT <<  N 0 Л 0 , то в

формулах (17а, б) мы пренебрегаем величиной RT . С учетом этих поправок формулы для химических потенциалов компонентов принимают вид:

А с = G С + ф СС + RT ln

(^L_ 1

'

к 3 — 4 х а 7

а

2 N ₀ Л)      п ² +

³      1 — х ^а с

(18а)

+ 3 RT [ 2 ( 1 — п ) ln ( 1 — п ) + ( 1 + 2 п ) ln ( 1 + 2 п ) — 3ln3 ] ;

'

А С е = 0 G C e + 3 RT ln

3 — 4 х.

. а 1

C

к 3(1 — х а ) 7

г + 3 n 0 Л)

< а 1 ^{2 х с}

а к 1 — хс 7

п ².

(18б)

Приравнивая химические потенциалы

^а‘= Ас ;А“е' = Аге, получаем уравнения равновесия тетрагонального феррита и аустенита:

62184 - 20,425 T + RT

ln

^ „а ^{х с} ,

к

-

ln

к 3 — 4 Х с 7

( х^Y Л к 1 — 2 х С 7

-

"3 N 0 Л)

^ уа х с

к

1-уа к1 х с 7

Т п ² +

( 19а)

1                                                      х ^

+- RT [ 2 ( 1 — п ) ln ( 1 — п ) + ( 1 + 2 п ) ln ( 1 + 2 п ) ] — 2-^ -

3                                             1 — х _с

( 21079 + 11,555 T ) = 0;

Физика

C          \

( 0 G Y e - 0 G ^ ) + RT

- 3 N A

/

' 2

xC-

1- Y “

V ^{1 x} c у

- 3ln

n ²

3 - 4 x ^

[ 3 ( 1 - x ? ) J

X Y x _C

1 —т Y

V ¹ x c у

+ In

f 1 - 2 x ^Y )

[ I -. J

C

^^^^^^

(21079 + 11,555 T ) = 0.

(19б)

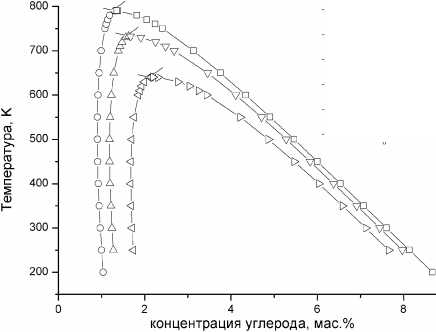
Третьим уравнением нашей системы выступает соотношение (8), в котором xС следует заменить на x^ • Оно отражает связь параметра порядка с концентрацией углерода в тетрагональном феррите. При этом требование устойчивости процесса упорядочения [16] приводит к условию 0,5 < п < 1. Решение системы уравнений (19а) и (19б) для различных значений температуры было выполнено численно в программном пакете Маthcad. Формально уравнения (19а, б) при фиксированной температуре можно рассматривать как задание пары функций xc = /1( xc ‘) и x«C = f2(xc'). Пример графиков подобных функции дан на рис. 2 для T = 700 К и Я0 = 10,5 эВ. Однако для физически реального корня x^ > xc , как это и наблюдается в действительности для сплавов железо-углерод. Для второго корня, наоборот, x^ ^ x^, что физически нереально, по- этому второй корень системы уравнений мы отбрасывали. Результаты расчета равновесных концентраций углерода в тетрагональном феррите и аустените показаны на рис. 3 для различных температур и значений константы деформационного взаимодействия Л0. По отношению к куби- ческому содержание углерода в тетрагональном феррите многократно увеличилось. Например, при 600 К содержание углерода в кубическом феррите составляет 0,011 мас. %, тогда как в тетрагональном – 0,92 мас. % (для λ0 = 10,5 эВ).

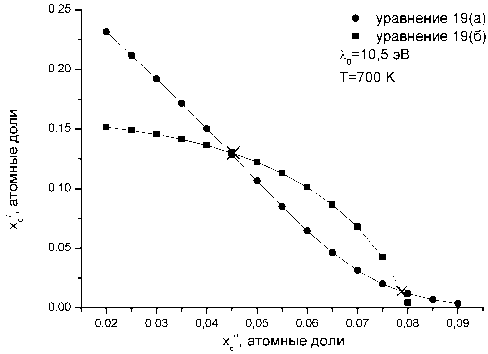
Рис. 2. Пересечение кривых зависимостей согласно уравнениям (19а) и (19б), показывающие существование двух корней (х) для этой системы

-о-с", Х0=10.5 эВ

С⁷, Х₀=10.5 эВ -а- с", Х₀=8.5 эВ —V— с⁷, \=8.5 эВ -<-с“, Х_о=6.5 эВ -▻— с⁷, \=6.5 эВ

Рис. 3. Пограничные концентрации углерода в мас. % для тетрагонального феррита и аустенита, полученные решением уравнений (19а) и (19б), для условий, когда выделение Fe 3 C подавлено

Данные рис. 3 отчетливо показывают, что с уменьшением величины Л 0 пограничная концентрация x ^ возрастает. При повышении температуры эта концентрация сначала слегка уменьшается, но в области высоких температур начинает возрастать. В то же время пограничная концентрация углерода в аустените монотонно снижается при возрастании температуры, так что эти две кривые смыкаются, как бы создавая купол. Для температур выше купола корней тетрагонального решения уже нет. При этом параметр порядка п = 0, т. е. могут существовать только кубические решения, и, соответственно, граничная концентрация углерода должна резко уменьшиться. В приведенном выше примере – в 90 раз. Но следует помнить, что в нашем рассмотрении на выделение карбидов был наложен запрет.

Мирзаев Д.А., Мирзоев А.А., Химические потенциалы тетрагонального феррита Булдашев И.В., Окишев К.Ю.и его равновесие с Y -фазой в сталях

Основной итог полученных результатов состоит в том, что пограничная концентрация углерода в тетрагональном бейните оказывается очень высокой по сравнению с равновесием кубический феррит/аустенит. В области высоких температур в реальности выделение карбидов Fe 3 C подавить невозможно, но в области 500–600 К, где бескарбидный бейнит может образовываться, следует ожидать сильнейшего возрастания углерода в нем до 1–1,2 мас. %.

Итоги работы

• 1.    На основе физической термодинамики сталей и теории Зинера–Хачатуряна для деформационного взаимодействия атомов углерода в мартенсите построены химические потенциалы углерода и железа для тетрагонального феррита в бейните

• 2.    Отличие представленной теории от теории Бхадешия состоит в том, что в ней более точно учтено как изменение энергии при z -упорядочении атомов углерода, так и энтропии, связанной с этим процессом.

• 3.    Используя условие равенства химических потенциалов, записаны уравнения равновесия компонентов и найдены решения полученной системы для различных температур и значений параметра деформационного взаимодействия λ ₀ . Построены диаграммы фазового равновесия ^a tetr ^ Y .

• 4.    Проведенный расчет поддерживает идею Бхадешия о том, что подавление карбидообра-зования при формировании бейнита приводит к резкому росту растворимости углерода в нем до 1,2 мас. %, что открывает новые возможности конструирования сталей на основе бескарбидного бейнита. Показано, что этот эффект связан с возникновением тетрагональности в бейните, аналогично мартенситу.

• 5.    Величина растворимости углерода в тетрагональном бейните зависит от температуры и параметра λ ₀ , на которую, вероятно, можно воздействовать целенаправленным легированием.

Настоящая работа поддержана грантом РНФ (16-19-10252).