Homomorphic Cryptosystem

Homomorphic encryption “Fig .1,” works on the concept of encrypting cipher text based on specific types of calculations and computations and generates an encrypted output which on decryption gives the result of calculations performed on the plaintext. [5]

Fully homomorphic encryption is a kind of ring homomorphism. Ring Homomorphism preserves the ring structure. We know real numbers are rings. Also the set of all 2×2 matrices is also a ring (under two matrix operations - addition an d multiplication) . If we define a function, f, between these rings as follows:

^=[a a]

Where a is a real number, then F is a homomorphism of rings,

F(a + b)= [a + b a + b]=[0  a]+[0  0]

=F(a) + F(b)              (1)

The above expression shows that F preserves additive homomorphism.

F( a . b) = [aob a"J = [a a]. [0 b]

= F (a) .F (b)

The above expression shows that F preserves multiplicative homomorphism.

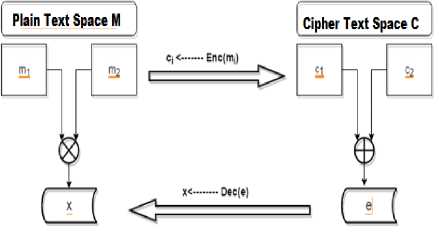
Fig.1. Homomorphic Property

Taking an Example, this explains the additive and multiplicative homomorphism.

• Example 1:

Consider a set of natural numbers with addition (+) operation.

F(y) = 9y

Any function which preserves addition homomorphism should follow property stated in equation (1)

F(a + b) = F(a) + F(b)

Now using the equation (1), F(y) = 9y can be written as

F(a + b) = 9(a + b) = 9a + 9b = F(a) + F(b).

• Example 2:

Consider a set of natural numbers with multiplication (. ) operation.

F(z) = 5z

Any function which preserves multiplication homomorphism should have the property stated in equation (2)

F(a . b) = F(a) . F(b) }

Now using the equation (2), F(z) = 5z can be written as

F(a . b) = 5(a . b) = 5a .5b = F(a) . F(b)

• II.   Homomorphic Encryption Techniques

There are many homomorphic encryption techniques which are explained below.

• A.    Multiplicative Homomorphic Encryption

• 1)    RSA: If the RSA public key is modulus N and exponent g, then the encryption of a message M is given by [14][16]

E(M) = M mod N            (3)

The homomorphic property unpadded RSA holds is:

E(M ) ⋅ Е(M ) = M M mod N

= (M M ) mod N = E(M M )       (4)

Thus if we consider two plaintext messages M1 and M2, multiply them and then encrypt the result using RSA, we get a cipher text.

The multiplicative property says that you can also encrypt each plaintext individually and then multiply the two corresponding cipher texts together and you can obtain exactly the same result.

However, for security reasons RSA has to add padding bits to a plain text message before encrypting it. This padding of the message results is losing the homomorphic property. [1] Also, RSA is only Partially Homomorphic since the additive property does not apply. Thus, it can be said that RSA is not semantically secure. [15]

• 2)    ELGAMAL Cryptosystem: It is defined over acyclic group G, this encryption scheme consists of following three sections, first is encryption, decryption and key generation.

Key Generation

There exists a cyclic group G of order d with generator

g

Alice randomly selects x such that x e {1,.....,d-1}

Calculate b = g                 (5)

Public Key: (G, g, d,b)

Private Key: x

Encryption

With Public key (G, g, d, b), Bob follows the following steps to encrypt plain text.

Chooses a random n = {1,…. , ԁ - 1}, calculates c = g

Calculates a shared secret s = b

Converts his secret message M , into Mʼ ϵ G and calculates c = Mʼ.ѕ

Sends the following cipher text to Alice.

(c ,c ) = ( g , Mʼ. ѕ)

Equation (9) becomes the cipher text to be sent to Alice.

Although if one knows Mʼ he can easily find b . Consequently, in order to improve security a new ʻnʼ, is generated for every message. Therefore n is also called an ephemeral key.

Decryption

To decrypt cipher text pair (c , c ) obtained in equation (9) with her private key x,

Alice computes the shared secret t = c and calculates

Mʼ=с .t =(M .s)(c )  =(M .b )(g  )

= (M .g .g ) = (M )         (10)

Homomorphic Property

ELGAMAL encryption scheme is a homomorphic scheme. This can be proved using example (3).

Let us consider example with two encryptions

• Example 3:

(c   , c ) = (g ,M b ),

(c , c )=(g ,M b )

Where n , n are randomly chosen from {1,…. . , ԁ -1} and M , M ϵ G , one can compute

(c , c ) (c  , c ) = ( c c ).( c c )

= ((g g ),(M b  M b ))

= ((g    ) ,(M M )b    ))        (11)

• B.    XOR Homomorphic Encryption

• 3)    Goldwasser–Micali Encryption Scheme :   A

probabilistic public-key encryption algorithm, the GM Encryption scheme has proven to be secure under standard cryptographic assumptions. [3]

It is the first semantically secure encryption scheme under the assumption that solving the quadratic residues problem is hard [4]. However, in GM encryption scheme cipher texts may be several times larger than the initial plaintext. This is because this scheme encrypts each bit of information and the length (size) of the resultant cipher text is equal to the length of the composite number п used in the scheme. Therefore it is not an efficient cryptosystem.

It consists of following three sections:

Key Generation

Choose two distinct random prime numbers р and q of similar bit-length.

Calculate N =  . q

Find a non-residue a such that

⁽r¹ )/ ² = -1 mod. p ,

^{(9 1} )/ ² = -1 mod q             (12)

Public key ∶ ( a , N ) Private key ∶ ( p , q )

Encryption

To encrypt plain text M with public key ( a , N ) ,

Bob first encodes M as a string of bits ( м_г , м₂ ,…, Mn ).

For every bit M_t , Bob generates a random value b_t , such that, gcd ( bt , N )= 1.

Calculate

Ct =  . a^Mi ( mod N )           (13)

Decryption

Alice receives ( Ci , c₂,…, C_n ) as cipher text from equation (13).

For each i , if C[ is a quadratic residue, M_t = 0, else M_t = 1,

Therefore message

M = ( м_г ,….,M„)            (14)

Goldwasser–Micali Encryption Scheme can be illustrated using example (4).

Example 4:

Key Generation

Let p =7, q =11

Where p =  = 3 ( mod 4)

Thus, N =   =77

Let a =6, where

6⁽ 7-1)/ ² = -1( mod 7),6⁽11-1)/ ² = -1( mod 11)

Public Key: (6,77)

Private Key: (7,11)

Encryption

To encrypt 3-bit message mim2m3 = 110.

Choose bi = 2, 6₂ = 3, Ьз = 5

Compute

Cl=22.61=24( mod 77)

C2 =32.61=54( mod 77)

C3=52.60=25( mod 77)

Ciphertext is (24,54,25)

Decryption

To decrypt Cipher text (24, 54, 25)

Compute

24⁽7-1 )/ ² = -1( mod 7)

54⁽7-1 )/ ² = -1( mod 7)

54⁽ 11-1)/ ² = -1( mod 11)

25⁽7-1 )/ ² = 1( mod 7)

This shows that 25 is quadratic residue and 24 and 54 are quadratic non-residue and thus the resultant plaintext is 110

Homomorphic Property

If ^1 , C2 are the encryptions of bits m₀ , т_г

Then ^1 , C2 ( mod N ) will be an encryption of M_Q ⨁ М_г

Let us consider

Cl =  . a^M^ ( mod N )

C₂ =  . a^M2 ( mod N )

We have

Ci . C₂ =( bi . a^M1 )( b₂ . a^M^ )( mod N )

=( btbl . a^M^^M^ ) mod N       (15)

Analyzing equation (15),

When A^o + Mi is either 0 or 1, we have

M_o + Mi =     ^⊕ Mi .

When Mq =    = 1  , Mq + Mi = 2 and

Cq Ci ( mod N ) is a quadratic residue and thus it is an encryption of 0. In this case also we have

M_o ⊕ Mi=1 ⊕ 1=0

• C.    Additive Homomorphic Encryption

• 1)    p aillier e ncryption s cheme : Paillier Cryptosystem is a probabilistic asymmetric key encryption scheme which uses different pairs of public and private key to encrypt and decrypt any plaintext. Paillier cryptosystem depends on a random element r for encryption per message bit.

Key Generation

Choose two large prime numbers and at random such that

(  ,( -1)( -1))=1

Calculate

=

Calculate

=    ( -1,  -1)

Select generator , such that

( (          - 1)/  ,)=1

Calculate

μ=( (          )) - 1      , where ( )=( -1)/ .

This function is only used on input values u that actually satisfy u = 1 mod n [6].

Public Key: ( ,)

Private Key: ( ,μ)

Encryption

Plaintext, where ∈ ℤ

Select random where

Compute cipher text as:

=     ∙

Decryption

As implied from equation (18),

Cipher text

Compute message:

т = L(ca тоd п)) ■ ц тоd п(19)

Paillier Encryption Scheme can be illustrated using the following example (5).

Example 5:

Key Generation

Let

= 49727  = 56737

=    = 2821360799

= 7960076758133918401

=    ( -1, -1) = 1410627168

Choose a random, = 1624691728

= 2197925655

μ = 1779031213

Public Key: (2821360799,1624691728)

Private Key: (1410627168,1779031213)

Encryption

Plaintext, = 1468689009

r = 1489472025

Cipher text

=     ∙            =

(956651757)         . (1489472025)

= 2015851325878209300

Decryption

= (         )∙         =

7960076758133918401).1779031213

= 1468689009

Homomorphic Property

Paillier Cryptosystem holds the property of additive homomorphism.

The product of two ciphers gives the sum of their corresponding plaintexts on decryption.

(  (   1 ,   1 ) ∗   (   2 ,   2 ))

=    1 +    2                    (20)

• III. Fully Homomorphic Encryption

Let (P,C,K,E,D) be an encryption scheme where [2][11]

P: Plaintext

• C:    Ciphertext

K: Keyspace

E: Encryption Algorithm

• D:    Decryption Algorithm.

Assume that the plaintexts form a ring (  ,⊗ ,⊕)

and the ciphertexts form a ring

( , ⊗ , ⊕ ) the encryption algorithm is a map from the ring to , i.e. ,

∶     →, where      is either a secret key or a public key .

For all and in and k in , if

( ) ⊕    ( ) =    (  ⊕    )(21)

( ) ⊗    ( ) =    (  ⊗    )(22)

then the encryption scheme is fully homomorphic.

• A. Classification of Fully Homomorphic Encryption

Let us begin with a space = {0,1}, plaintext space, and a family of functions from tuples of plaintexts to , expressed as a Boolean circuit on its inputs, referred by . [7]

Input tuple (    ,    ,...,    ) denotes the plain text.

The classification of fully homomorphic encryption is depicted in Fig. 2. Corresponding definitions and explanation about each classification can be found in the following subheadings.

• 1)    I – Evaluation Policy

Let ℓ be a set of circuits. A ℓ –evaluation policy for ℓ is a tuple of probabilistic polynomial–time algorithms ( KeyGen , Encr , Eval , Deer ) such that:

The key generation algorithm, KeyGen (1 Л ,ɑ) , takes two inputs, security parameter Л and an auxiliary input ɑ, and outputs a key triplet ( p , s , e ), where p denotes the public encryption key used for encryption, s denotes the secret key used for decryption and e denotes the evaluation key used for evaluation.

The encryption algorithm, Encr ( p , m ), takes a plaintext m and the public encryption key p and as inputs and outputs a cipher text c .

The evaluation algorithm, Eval(e, C, c ,...,cn), takes a circuit C ∈ ℓ , the evaluation key e and a tuple of inputs that can be a mix of ciphertexts and previous evaluation results as inputs and generates an evaluation output.

The decryption algorithm, (sк,c), accepts the secret key s and either a ciphertext or an evaluation output and produces a plaintext m.

Assuming the following convention,

X denotes the ciphertext space и denotes the space of evaluation outputs, and z is the union of both X and Y.

z ^∗ contains arbitrary length tuples made up of elements in Z.

The key spaces are denoted by , Xs and , ^e , respectively for p,s and e.

The public key contains a description of the plaintext and ciphertext spaces.

ℓ is the set of permissible circuits, i.e. all the allowed circuits which the evaluation policy can evaluate.

The domain and range of the algorithms are given by

KeyGen: N × A → X_p × X_s × "Ke

Encr: ^p ×M→ X

Decr: %_s × z → M

Eval: Xe × ℓ ×z∗ → •y where X∪U= and A is an auxiliary space.

Formally,

X = {c |Pr[Encr(p, m) = c]> 0, m ∈ p },   (23)

X in equation (23) can be considered an image of encryption.

And

У = { z |Pr[Eval(e, C ,c i ,...,c n )= z ]> 0, ci ∈ z , anԁ C ∈ ℓ },                (24)

"У in equation (24) can be considered an image of evaluation.

• a)    Strict Decryption

Any ℓ– evaluation policy (KeyGen , Encr , Eval , Deer ) is said to correctly decrypt if for all m ∈ P ,

Pr [ Deer ( s , Encr ( P , m )) = m ] = 1,      (25)

Where s and p are outputs of KeyGen (1 Л ,ɑ).

This means that we must be able to decrypt a cipher text to the correct plaintext, without any error. [8]

• b)    Strict Evaluation

Any ℓ –evaluation policy ( KeyGen , Encr , Eval , Deer ) is said to correctly evaluate all circuits in c if for all c_t ∈ X where m_t ← Deer ( s , ci ), for every C ∈ ℓ , and some negligible function E , it satisfies equation (26).

Pr[ Deer ( s , Eval ( e , C , Ci,...,c_n))= C (_mi,..., m_n )] = 1 - e (Л)                 (26)

Where s, p and. e are outputs of KeyGen (1 Л,ɑ)

This means that decryption of the homomorphic evaluation of an allowed circuit yields the correct result. [7][12,Def 3.3]

Thus, it can be said that a ℓ- evaluation scheme is correct if it has the properties of both correct evaluation and correct decryption.

Consequently the encryption scheme is Somewhat Homomorphic.

• 2)    Somewhat Homomorphic Encryption

Any ℓ –evaluation policy ( KeyGen , Encr , Eval , Deer ) that holds a correct and valid decryption as well as an evaluation is called Somewhat Homomorphic Encryption Scheme (SHE).

This level of homomorphic encryption doesn’t require Compactness, and as a result the size of the cipher text can substantially increase with each homomorphic operation. Also, while making the set of permissible circuits, C, there is no requirement to mention which circuits this must include.

Secret Key Somewhat Homomorphic Encryption

KeyGen : From some interval p e [2^ɳ' ¹,2^ɳ], choose an odd integer which acts as a secret key for encryption.

Encr ( pk , m ) : In order to encrypt plain text bit, 6 {0,1}:

Choose an integer whose residue mod p has the same parity as the plaintext and set the cipher text as this integer.

Namely, set c=    + 2r+m;           (27)

Where q and r are chosen randomly in some other intervals, such that p /2 is greater than 2 r in absolute value.

Decr (p, c) : Given a cipher text c and the secret key p, output m = (c(mod p))(mod 2) = ((pq + 27 + m)mod(p))(mod 2)

= 27 + m (mod 2) = m        (28)

• Example 6:

Suppose p= 23 ; bit to encrypt m = 1,

Then c = 23.2 + 2.0 + 1 = 47, where q = 2, r = 0

Now to decrypt it back to m, m = (c(mod p))(mod 2)

= (47 mod 23) (mod 2) = 1 (mod 2) = 1 = m

Property of Fully Homomorphic Encryption

Suppose we have two cipher texts, c 1 = pqi + 27 + mi and c2 = p q2 + 2r-2 + m2

Then

C i + C 2 = (p(q i + q 2 ) + 2⁽7- i + 7 2 ) + ⁽m i + m 2 ))

C i . C 2 = (p . q i . q 2 +2 q i 7 + 2 q 2 r i + m i + q i m 2 )p + 2(2 7 7-2 + 7-2 m i + 7 m 2 ) + (m i m 2 ) (30)

When

(7 + Г2)  

2 77 + 7 mi + 7 m2 < p/2

Thus we have,

(Ci + c2(mod p))mod 2) = mi + m 2

(ci. c2 (mod p))mod 2) = mP m2

• Example 7:

Let p = 23, m i = 0    m 2 = 1, qi = 1 ,q2 = 2/7 = 1,72 = 2

ci = 23.1 + 2.1 + 0 = 25

c2 = 23.2 + 2.2 + 1 = 51

Now,

(C i + c₂(mod p))mod 2)

= ((25 + 51)(    23))(    2)

= 76(mod 23)(mod 2) = 7 mod 2 = 1

= m i + m 2

And

(ci. c2(mod p))mod 2) =(25.51) (mod 23))(mod 2) = 1275(mod 23)(mod

= 10 mod 2=0 = mi.m2

However, it has been seen that while using the fully homomorphic property to evaluate a Boolean function f (m_i,m ₂ ... ,m_n) where m_t б{ 0,1} , given c_t , the encryption of m , , for i = 1,2,..., n.

As the number of the additions and multiplications in the Boolean function grow so does the size of the noise component 7 in the resultant cipher text. Consequently the size of the noise component is proportional to the number of operations.

And hence only low-degree Boolean functions (circuits) can be evaluated over encrypted data.

This is the reason this scheme is termed Somewhat Homomorphic.

• a)    Compactness

A Somewhat Homomorphic Scheme (SHE) is said to be compact if there exists a polynomial q = q(λ) , such that for any key-triplet   (s,p , e) generated by

KeyGen (1^я , a), any circuit С E I and all cipher texts C[ E X, the size of the output from Eval (e,C, c 1 ,....., c_n)

is at most q(λ) bits long (regardless of the number of inputs or C).

According to Craig Gentry, if in addition the run time of the decryption circuit depends only on λ and not on any of its inputs, the scheme is said to compactly evaluate C. (Gentry, 2014)

However it was observed [8] that any l - evaluation policy (KeyGe n,EnC7, E va I , Dec 7) compactly evaluates all circuits in I if the scheme is compact and correct.

This implies that the cipher text size doesn’t grow much during homomorphic operations and the output size depends on the security parameter, λ, only.

• b)    Circuit Privacy

Anyl- evaluation policy (KeyGen, Encr, Ev а I, De C7) is said to be perfectly/statistically/computationally circuit private if for any key-triple ( , , ) output by (1 , a) , for all circuits C E C and all c e X, such that m, ^

• ( ,  ), the two distributions on

D i = Eval( e,C,C i......... c „ )        (33)

And

D₂ = Enc(p,C(m i ,,,,,,,m_n)         (34)

both taken over the randomness of each algorithm, are perfectly,      statistically      or      computationally indistinguishable, respectively.[8]

• 3)    Levelled Homomorphic Encryption

AI - Evaluation p о Iicy (KeyGe n, En ст, EaaI, De cr) is said to be “levelled homomorphic” if its key generation algorithm, KeyGen, accepts an auxiliary input a = d which clearly identifies the maximum depth (size) of circuits that can be evaluated. Also the encryption should be correct, compact and the length of evaluation output should not depend on depth, d of the circuit. ( [7], d ef . 3.6 )

• 4)    Fully Levelled Homomorphic Encryption

A I - Evaluation policy (KeyGe n,Encr , EaaI, De cr) is said to be “fully levelled homomorphic” if the set I is the set of all binary circuits with depth atmost d.

Apparently, in Somewhat Homomorphic Encryption, the depth of the circuit can vary depending on a parameter. This means that the length of cipher text will increase depending on the depth of the permissible circuits. However, this is not the case with Levelled Homomorphic Encryption in which the length of the cipher text does not depend on the depth , of the circuit.

• 5)    Fully Homomorphic Encryption

A fully homomorphic encryption scheme is a ℓ -evaluation (         ,      ,      ,      ) that is compact, correct and where ℓ is the set of all circuits. ([7], def. 3.5)[9].

В о о tstrap ab iI ity is a condition in which the degree of the evaluation polynomial that is to be applied on cipher text exceeds the degree of the decryption polynomial. Once the scheme becomes bootstrappable it can be converted into a fully homomorphic encryption scheme by entering the encryption of the secret key bits inside the public key. [10] . According to Gentry, a somewhat encryption scheme can be converted into fully homomorphic encryption using boot strapping . [12]

Given a homomorphic scheme, we can homomorphically compute any function. Theoretically we can: [13]

• •    Encrypt the encrypted data with a new key

• •    Encrypt the old key with the new one

• •    Evaluate     the     decryption     procedure

homomorphically, thereby resulting in a cipher text encrypted with the second key.

Based on Gentry’s approach, two different fully homomorphic schemes are known: Gentry’s scheme [11] based on ideal lattices and a scheme by van Dijk, Gentry, Halevi and Vaikuntanathan (DGHV) over the integers which appeared at Eurocrypt 2010 [9].

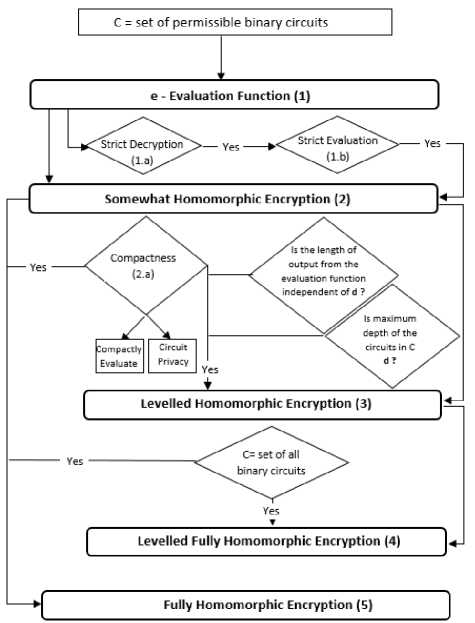
Fig.2. Classification of Fully Homomorphic Encryption

• IV. Conclusion

This paper provides its readers with the basic idea and mechanism involved in the recently evolved homomorphic and fully homomorphic encryption schemes.

Using homomorphic encryption to secure data prevents plain text from being exposed. Thus, homomorphic encryption has given a new dimension to cloud storage and security. There are various homomorphic cryptosystems available and now there is a need to develop Fully Homomorphic cryptosystems which meet all the criteria of being compact, correct and applicable on all functions/circuits. With the advent of Fully Homomorphic Cryptosystem, the data has become semantically secure.

Acknowledgement

I am highly indebted to Dr. Meena Kumari for not just providing guidance and supervision but also for providing encouragement and necessary information while carrying out research on this topic. I would like to express my gratitude towards Ms. Mehak Khurana for her kind co-operation and guidance which helped me accomplish this paper. My thanks and appreciations also go to my colleagues in developing the research base and people who have willingly helped me out with their abilities.