Хрупкое разрушение ледяного слоя при понижении уровня воды
Автор: Богульский И.О.
Журнал: Вестник Красноярского государственного аграрного университета @vestnik-kgau
Рубрика: Технические науки
Статья в выпуске: 4, 2018 года.
Бесплатный доступ
Настоящая работа продолжает изучение пове-дения толстого ледяного поля, плавающего на поверхности воды, при понижении уровня воды. Ранее рассматривалась стационарная задача о равновесии ледяного слоя вблизи плоского участка берега. Были изучены различные способы контак-та с берегом, получено напряженно-деформируемое состояние ледяного поля, как со свободной верхней поверхностью, так и нагружен-ного некоторой силой; выполнена оценка «опасной зоны». Натурные наблюдения разрушения льда говорят о наличии в ледяном поле двух характер-ных трещин: в месте контакта с берегом и на расстоянии 10-12 толщин. Однако в рамках ста-ционарной задачи не удается объяснить возникно-вение второй трещины. Все это приводит к необ-ходимости рассматривать динамику поведения ледяного поля после возникновения первой трещи- ны. В работе сделана попытка смоделировать поведение льда таким образом, чтобы напряжен-ное состояние ледяного слоя давало концентра-цию растягивающих напряжений вблизи берега и на некотором расстоянии от него, что, вероятно, и обеспечивает разрушение вблизи этих участков. В работе получено приближенное решение динами-ческой контактной задачи, учитывающей несжи-маемость воды, на которой плавает лед. Учет несжимаемостии приводит к подпору ледяного поля водой и быстрому возникновению второй трещины. При численном решении задачи возникли серьезные трудности. Решение было основано на методах операционного исчисления. К краевой за-даче для системы дифференциальных уравнений с частными производными от функций с тремя пе-ременными было применено преобразование Лапласа по времени и косинус-преобразование Фурье по одной из пространственных переменных. Ограниченное решение полученной системы обык-новенных дифференциальных уравнений удалось выписать в виде сходящихся несобственных инте-гралов. Численное обращение преобразования Лапласа изображения неизвестной функции вызва-ло наибольшие трудности. Известные методы численного обращения оказались неприемлемы, так как они требуют знания порядка убывания изображения. Обращение пришлось делать с по-мощью синус- и косинус-преобразования Фурье с большим количеством узлов интегрировния. Вы-числения обеспечили необходимую точность.
Численное моделирование, упругая пластина, ортогональные полиномы
Короткий адрес: https://sciup.org/140224429
IDR: 140224429 | УДК: 539.3+532.5
Текст научной статьи Хрупкое разрушение ледяного слоя при понижении уровня воды
Введение. Рассматривается динамическая задача о движении тяжелого ледяного поля, плавающего на поверхности воды после «мгновенной» смены граничных условий, связанной с возникновением трещины в месте контакта с берегом.
В рамках стационарной задачи не удается объяснить возникновение второй трещины. Это приводит к необходимости рассматривать динамику поведения ледяного поля после возникновения первой трещины, учитывать несжимаемость воды и инерционные члены, которые могут дать дополнительные растягивающие напряжения в слое.
Решение сформулированной динамической контактной задачи плоского упругого слоя и идеальной несжимаемой жидкости выявляет концентрацию существенных растягивающих напряжений на некотором участке, что обосновывает экспериментальный факт возникновения второй трещины.
Динамика упругого слоя на упругом основании. Рассмотрим задачу о движении упругого слоя под действием собственного веса на упругом основании. Пусть ледяное поле представляет собой по-лубесконечную упругую пластину толщиной ℎ (рис. 1). Движение вызывается резкой сменой граничных условий. Левый торец, будучи начально жестко закрепленным в месте контакта с берегом, после возникновения трещины в месте заделки «мгновенно» освобождается, оставаясь опертым о берег. Таким образом, возникает возможность вращения вокруг точки опоры.
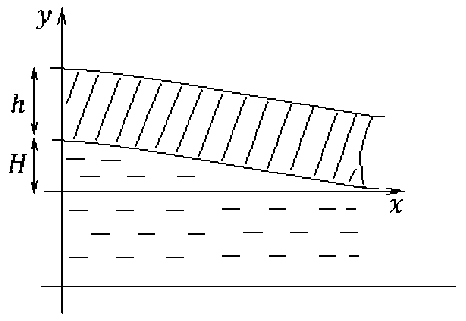
Рис. 1. Полубесконечный упругий слой
Задача состоит в определении в области D ={0≤У≤ℎ,0≤x≤∞ } компонент тензора напряжений ^ , , и вектора смещений и,V, являющимися функциями координат
X , У и времени t .
Неизвестные функции удовлетворяют в области D уравнениям движения д^ дт12 д2и дт12 до2d
+ = , + + ху = закону Гука ди ди ди ди диди
^i = + ^ч~ , ^2 = +а —, ^1 =( +), дх ду дх ду ду дх
где а = +2 у ; Р = ; и l-i – упругие постоянные Ламе; X – проекция плотности массовых сил на ось У , граничным условиям на У =0 и У =ℎ .
Т12 | y-h =0, °2 | y-h =0, Т12 |у=о =0, ^2 | у=о =- Хус ( и | у-о - к ℎ).
Считаем, что неизвестные функции ограничены при х →∞ . На левом торце х =0 выполнены граничные условия
∫
и ( X , У , t )| Х=О^У =∫ и ( X , У , t )| =
'О ^0
=∫ ( X , У , t )| Х-0
Jo
(2 У -ℎ) dy =0.
Это означает, что торец имеет возможность вращаться. В начальный момент времени смещения и и и точек слоя известны и совпадают с решением статической задачи о равновесии упругого слоя c граничными условиями типа «жестко заделанного торца». Движение начинается без начальной скорости:
ди ( х , У , t ) = ди ( х , У , t )
| =0, | =0.
Приближенное решение динамической задачи . Решение получим предложенным в [1] методом.
Неизвестные функции dt , Qi , St Ui , vi представляют собой первые члены разложения искомых компонент тензора напряжений и вектора смещений в ряды по полиномам Лежандра по толщине пластины и являются теперь функциями координаты x и времени t .
Таким образом, мы приходим к смешанной задаче для системы дифференциальных уравнений с двумя независимыми переменными.
Эта система уравнений имеет вид
d[ =3 Pso +p⁄ у ̈ ;1 ;
_ P2b⁄и+P u- so = ⁄2 и+⁄у;
u[ =⁄ dr ; u' =- .
Граничные условия для этой системы имеют вид и (0)= H ; d± (0)= 0.
Начальные условия являются решением стационарной задачи
V | t=o = [cos( bpx ) +sin( bpx )] ,
Vt | t=o =0.
В итоге задача приводится к смешанной задаче для уравнений в частных производных четвертого порядка
̈⁄ tt + К ( IV )+4 V =0;
V | x=o = ; К" |X=0 =0;
V | t=Q = ( cosx + sinx ); Vt | t=Q =0.
Решать задачу будем методом разделения переменных, линейной заменой сделав краевые условия однородными.
Пусть V= T ( t ) X ( x ) , тогда
TX+̈nX(IV)+4TX=0, где X' |x=o = |x=o =0, а X ограничено при x→∞.
В итоге получаем краевую задачу для определения X
X ( IV )+4(1+ v ) X =0 , X | x=o = | X=0 =0.
Окончательно полным решением задачи будет
V ( X , t )=
∫0a( A ) cos.t√ A4 +4/+
— 00
+ b(A)sin.t√A4 +4/1sin Ax dA, где функции a(A) иb(A) следует определять из начальных условий
0=
CO
∫ b ( A )√ A4 +4sin Ax dA ,
— 00
=
∫ a ( A )sin Ax dA .
— 00
Таким образом, a ( A ) и b ( A ) являются функциями разложения начальных условий в синус-интеграл Фурье, следовательно,
V ( x , t )=
— ∫ “ cos( t √ A4 +4) sin Ax dA .
IT .
Окончательное решение задачи имеет вид
V ( x , t )=
4 H f“ A — ,
=∫ A4 +4 cos. t √ A4 +4/ sinAx dA +
+ He Xcosx .
Интеграл вычислялся численно методом с равностоящими узлами для вычисления синус- и коси-нус-интегралов Фурье [2] и по формуле трапеции по A . Было выбрано 5000 узлов интегрирования, что обеспечило точность порядка 10 -4 при вычислении V ( x , t ) .
Для некоторых моментов времени кривые V ( x , t ) и °i ( X , t ) приведены на рисунках 2 и 3. Решение позволяет проследить движение упругой пластины вплоть до выхода на стационарное решение.
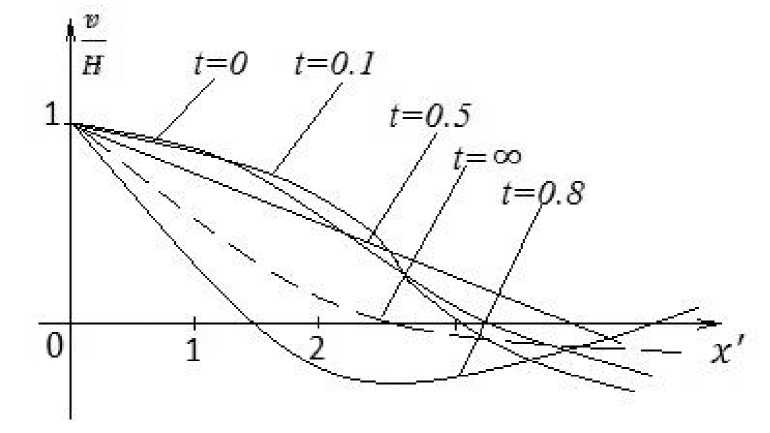
Рис. 2. Прогиб срединной поверхности упругого слоя
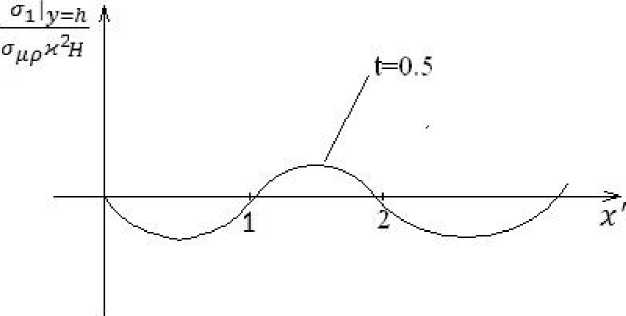
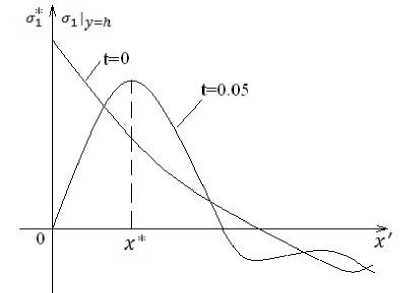
Рис. 3. Напряжения в упругом слое
Тем не менее необходимо признать, что описание процесса движения тяжелой полосы в рамках модели, рассматривающей воду лишь как упругое основание, не позволяет объяснить возникновение второй трещины. Учтем условие несжимаемости воды, которое при наличии близкой стенки, очевидно, обеспечит подпор упругого слоя жидкостью. Подобные постановки рассматривались в [3].
Динамическая контактная задача . Пусть в области II: {-от<у<у|у =0 , 0 < х < от}
(рис. 4) потенциал скорости ((х,у, t) и давление в жидкости Р %х,у , t) удовлетворяют уравнению несжимаемости
VxX + Фуу 0
Таким образом, предлагается сформулировать и интегралу Коши – Лагранжа плоскую задачу о контакте упругой полубесконечной
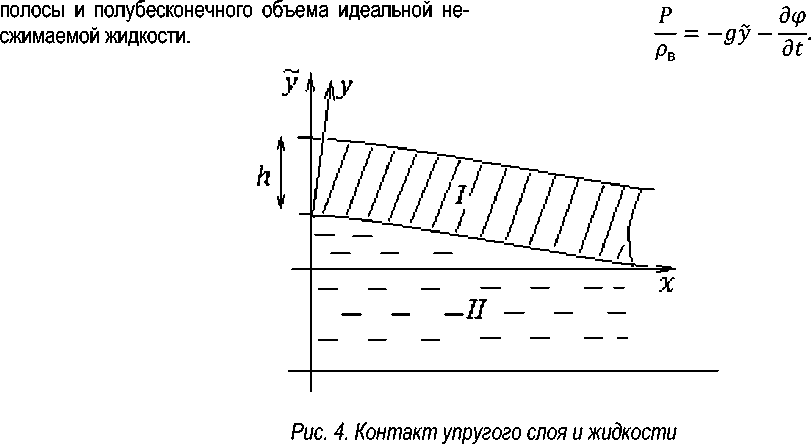
На границе выполнено условие непротекания через стенку: ^ |ж =0 = 0. Потребуем, чтобы У (x,y,t) и Р (x,y,t) были ограничены при х ^ от, уу ^ от.
В области I: {0 < у < h, 0 < х < от} компоненты вектора смещений и и V и тензора напряжений or, &2, т2 2 удовлетворяют сформулированным в предыдущем разделе уравнениям движения, закону Гука, граничным условиям на поверхности и краевым условиям на левом торце х = 0.
В начальный момент функции и и V - есть решение стационарной задачи с условием на торце в виде «жесткой заделки», и движение начинается без начальной скорости, т.е. иt = Vt = 0. Кроме того, выполнены условия контакта пластины с жидкостью: совпадение скоростей
д(р dV yy Ьу =v|y=о = у |y=0, и равенство давлений
°2 |У=0 = | ̃ =v | y=0 .
Здесь ̃, X – неподвижные эйлеровы координаты; У , x – лагранжевы координаты; связанные с упругим слоем; p в – плотность воды; 9 – ускорение свободного падения. Задача состоит в определении неизвестных функций (p , P , и , V , ^i , °2 , ^12, удовлетворяющих сформулированным выше дифференциальным уравнениям, граничным и начальным условиям и условиям контакта.
Построение приближенного решения. Предлагается приближенно определять напряженно- деформируемое состояние упругой пластины (обл. I), а линеаризованное течение жидкости в обл. II определять точно. Линеаризация проводится так же, как и в [4], при изучении волн на свободной поверхности. В качестве приближенного метода принимается используемый выше, при решении динамической задачи, подход, основанный на разложении неизвестных функций в ряды по толщине пластины по полиномам Лежандра.
В итоге задача в первом приближении (с учетом малости параметра X) сводится к краевой задаче для уравнения Лапласа в четверти плоскости:
Ф x' x'+Ф y' y'
=0,
Vt't'
+
V
(
7
)+4
V
+
m |y'=o=0, Фх' |x^o"0,Фу' |y'=o=Vt't', ^x' x'|x'-O =0, v|x'-O = , Vp |t'=0 =0, V| t'=0 Здесь введены безразмерные переменные x' = , y' = , t' =√9 ⁄4ℎ t, = 1⁄2X≈25, p = 2⁄ℎ. В дальнейшем штрихи будем опускать. = (cosx' + sinx'). Задача сводится к интегро-дифференциальному уравнению следующим образом. Для задачи Неймана для ip можно выписать функцию Грина 1 ( 1 1 G(x,У,f,V)=- — In {[(f-X)2+(V-У)2]2 [(f+x)2+(V-У)2]2 [(f+x)2 2 ( +(V+У)2]2 [( f -x)2+(9+У)2]2 }. Затем выразить решение через функцию Грина и У→0. Тогда для определения функции V получим неизвестную пока функцию Vи выписать (p при интегродифференциальное уравнение I'll +к( „ )+4v+я∫ In | x2 - f2 | Vtt (f) d^=0. Анализ уравнения показывает, что учет несжимаемости вносит в уравнение динамики дополнительное слагаемое того же порядка, что и имеющиеся. Будем решать смешанную задачу для системы дифференциальных уравнений. К системе уравнений Фхх+Фуу=0, Utt +к(IV)+4v+ m (p | = 0, ̃ XX + ̃ 'yy =0, ̃У|y=o = ̃-sHe Xsinx, ̃ 'x | X=0 =0, где величины с «волной» – изображение по Лапласу соответствующих функций. Умножим эти уравнения на cos Ax (A≥0) и проинтегрируем поx от 0 до ∞. Получающаяся система обыкновенных дифференциальных уравнений по У для косинус-преобразований Фурье неизвестных функций, ограниченных при У→-∞, имеет тривиальное решение. Окончательно + +P(s)2∫ я Jo 2 ' a(s)∫ я Jo ̃(x,s)=a(s)e~x + AcosAx dA [A5 +A(s2+4)+m s2] + [A3-A(s2+4)-ms2] cosAx dA (A2+1)[A3 +A(s2+4)+m s2] + 2 Hs С co (2+л2)(л+т) cosAx dA +п∫ (А2 +4)[А3 +А(s2+4)+т s2], Р(s)= ^2^6 - ^3^5 Л^5 + ^2 , а(s)= hh + Л^б Л4 + ^2 2 2 [ - ( +4)- ] П∫[А5 +А(S2+4)+ms2],h =1+11∫(А2+1)[А5 +А(s2+4)+ms2], о о . 2SH Г ОО (А+т)(2-А2) dA_____ . _ 2 Г ОО [А(S2+4)+ms2]dA = ∫) (Л4+4)[л5+л (S2+4) +ms2] , 15 = ∫) [л5+л (S2+4) +ms2], 2 sH (A+m)(2-A2 )A2dA /б=- П ∫(A4+4)[A5 +A(s2+4)+ms2]. о Оригинал V(x,t)определяется по изображению ̃ (X,s) через интеграл Меллина c+ico V(x,t)=1 ∫ est ̃(x,s) ds . 2 nt J c-ico Все интегралы вычислялись на основе метода с равностоящими узлами. Обеспечивалась точность их вычисления до четвертого знака. Не удалось применить специальные методы численного обращения преобразования Лапласа, для использования которых необходимо знать поря- док убывания изображения по S. Интеграл Меллина просто сводился к синус- и косинус-интегралам Фурье. Было замечено, что изображение «медленно» убывает по s, что потребовало для получения необходимой точности большого количества узлов интегрирования. Выводы. На рисунках 5 и 6 приведены прогибы V(X,t) и напряжения al (X,t) на верхней поверхности пластины У=ℎ в начальный момент времени t=0 и в момент времениt = 0,05 с. Рис. 5. Прогиб срединной поверхности упругого слоя Рис. 6. Напряжения в упругом слое На рисунке 6 при t = 0,05 с видна существенная концентрация растягивающих напряжений в упругом слое на расстоянии приблизительно 10–12 толщин льда. Можно считать, что моделирование процесса хрупкого разрушения льда в рамках динамической контактной задачи упругого слоя и несжимаемой жидкости качественно описывает поведение ледяного поля, и факт появления второй трещины в рамках данной модели достаточно обоснован.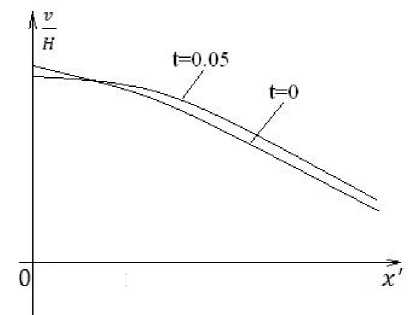
Список литературы Хрупкое разрушение ледяного слоя при понижении уровня воды
- Иванов Г.В. Решение плоской смешанной задачи теории упругости в виде рядов по полиномам Лежандра//Прикладная механика и техническая физика. -1976. -№ 6. -С. 27-34.
- Крылов В.И., Шульгина Л.Т. Справочная книга по численному интегрированию. -М.: Наука, 1966. -370 с.
- Слепян Л.И. Нестационарные упругие волны. -Л.: Судостроение, 1972. -376 с.
- Кочин Н.Е., Кибель И.А., Розе Н.В. Теоретическая гидромеханика. -М.: Физматгиз, 1963. -Ч. I.


