Hybrid Black Hole Algorithm for Bi-Criteria Job Scheduling on Parallel Machines

Published Online April 2016 in MECS DOI: 10.5815/ijisa.2016.04.01

Nature has always been a source of inspiration for human beings. This is reflected by recent technological advances in various fields of science and engineering [1]. Bat, Firefly, Artificial Bee Colony, Cuckoo Search, Flower Pollination, Black Hole and Grey Wolf algorithms are few algorithms that have been developed by taking inspiration from nature. These algorithms are widely used for solving various engineering and manufacturing optimization problems in various fields ranging from routing in wireless sensor networks to scheduling of jobs in manufacturing unit [2-11]. Such engineering optimization problems are generally accompanied by multiple and often conflicting objectives or criteria, and are quite challenging to be solved.

Inspired from various applications of nature-inspired algorithms, we investigated the usage of nature-inspired

Black Hole algorithm for optimizing scheduling of jobs on parallel machine on the basis of criteria namely Maximum Tardiness ( T_max ) and Weighted Flow Time ( WFT ).

In engineering and manufacturing problems, there are often job instances with different processing times, due dates and priorities. Parallel machine scheduling involves a scheduling environment with m identical, parallel machines. Each of the n given jobs must be processed non-preemptively on any one of the available machines. However, machines can process jobs unattended. The problem of scheduling multiple jobs on parallel potential machines by optimizing T_max and WFT is one of the important problems that have been repeatedly encountered by engineers.

• A. Migration from Single Objective to Multi-Objective Black Hole Algorithm

When compared with single objective optimization, multi-objective optimization is quite cumbersome [12]. This is quite evident from their theory of approach. In case of single objective optimization techniques, the solution is a single point in the solution space. On the other hand, in case of multi-objective optimization technique numbers of equally optimal solutions in the solution space are identified. This set of multiple optimal solutions is called Pareto front. This Pareto front is composed of solutions with relationships that define the superiority of one solution over another. More formally, for cost minimization problems, the relation between solutions is defined as follows:

F ( x 1) >  F ( x 2), if ^ g , fg ( x 1) >  fg ( x 2)

where f_g is the value of g^th fitness function and F(x) is the overall fitness of the solution x; g varies from 1 to h where h is the number of objectives to be optimized

This means solution x2 is better than x1 if it is better according to at least one of the individual fitness (objective) functions and no worse according to all of the rest. In other words, x2 dominates x1. The Pareto front is the set of elements that are not dominated by any possible element of the solution space. The Pareto front thus denotes the best results achievable.

Generally, a single objective optimization algorithm cannot be used directly as multi-objective optimization technique [13]. Various techniques have been devised to adapt single objective approaches to multiple objective approaches. One such technique is to reformulate the problem under consideration as a single objective problem. This is possible by adding relative weights to the objectives and performing weighted summation of multiple objectives to make a single objective [14]. The approach now follows single objective method of optimization to identify best solution with optimum weighted sum of objectives. Another way is to find set of equally optimal non-dominated Pareto front [15]. So, it has been observed that significant changes are required to modify single objective to multi-objective optimization technique.

In this paper, multi-objective Black Hole algorithms have been developed from single-objective approach for optimizing bi-criteria namely maximum tardiness (T max ) and weighted flow time (WFT) for the jobs to be scheduled on parallel machines. Black Hole [16] has been inspired by black hole theory of the universe. This theory describes a black hole as a place in space where gravitational force is so strong that even light can’t escape. Efficiency and performance of proposed algorithms have been compared to existing state of art optimization algorithms. The results thus obtained are statistically tested and indicate that proposed algorithms significantly outperforms the existing algorithms for the problem of scheduling jobs on parallel machines.

The prime contributions of this research work are listed below.

• •    Formulation and investigation of the use of Black Hole algorithm as multi-objective optimization technique using weighted sum of objectives for the process of job scheduling on parallel machines on the basis of bi-criteria namely T max and WFT.

• •    Investigation of the impact of hybridizing multiobjective Black Hole algorithm with Genetic Algorithm (GA).

• •    Formulation and investigation of the application of Black Hole algorithm as multi-objective optimization technique (using auxiliary archive for external storage of Pareto front solution) for the process of job scheduling on parallel machines on the basis of bi-criteria namely T_max and WFT.

• •    Investigation of the impact of developing multiobjective Black Hole algorithm by using auxiliary archive as well as GA.

• •    Comparison of proposed algorithms to that of existing Multi-Objective Genetic Algorithm (MOGA), Non-dominated Sorting Genetic Algorithm-II (NSGA-II) and Multi-objective Particle Swarm Optimization (MOPSO) algorithms with respect to job scheduling on parallel machines.

The rest of paper is organized as follows. In Section II, literature related to the field of job scheduling on parallel machines using nature-inspired algorithms has been summarized. Section III addresses the formulation of the problem along with various assumptions, notations and fitness functions. Section IV describes the proposed multi-objective Black Hole algorithms. Section V describes the experimental setup and assessment criteria. In Section VI, scheduling results of randomly generated samples are empirically and statistically investigated. In Section VII, threats to the validity of the proposed work have been discussed. The paper is concluded in Section VIII mentioning some future recommendations.

• II.    Literature Review

Scheduling of jobs on parallel machines has been an upcoming research topic in the past couple of decades. A large number of engineers and researchers have been working to perform optimization of multiple criteria for scheduling number of jobs on parallel machines. Various meta-heuristic approaches have been developed to solve this problem. In this section some of these approaches have been discussed along with the criteria and heuristic followed.

In one of the works in the field of job shop scheduling, Ruiz-Torres et al. [17] minimized the number of late jobs and their average flow-time. They used simulated annealing and neighborhood search for this task. In another work [18], Rahimi-Vahedet et al. minimized the weighted mean completion time and weighted mean tardiness using Multi-Objective Scatter Search (MOSS). Chang et al. [19] optimized production and marketing using Ant Colony Optimization (ACO) technique for solving the problem of multi-stage job shop parallel machine scheduling. They also incorporated the concept of order splitting for multi-stage scheduling of jobs.

In another work [20], total completion time and makespan are minimized while scheduling jobs on m machines taking into consideration the sequence dependent set up times of jobs and by using heuristics such as Shortest Sum of Setup, Processing and Removal Times (SSPRT), Shortest sum of Setup and Removal Times (SSRT) and Earliest Due Date (EDD) sequence. Berrichi et al. [21] used evolutionary genetic algorithms to minimize makespan and system unavailability while scheduling n jobs on m machines. The Pareto front thus obtained is approximated to obtain the desired optimized schedules.

Berrichi et al. [22] proposed multi-objective ACO based approach to optimize production and maintenance scheduling. The goal of their approach is to identify the best assignment of production tasks to machines along with the reduction in preventive maintenance (PM) periods of the production system.

Mazdeh et al. [23] used a meta-heuristic algorithm based on Tabu search to minimize the total tardiness and machine deteriorating cost.

Hybrid genetic algorithm based on the concept of multiple subpopulations has been used by Rashidi et al. [24] to minimize the makespan and maximum tardiness while scheduling jobs on unrelated parallel machines, taking into consideration the setup times of jobs.

Artificial immune systems have been investigated [25] for solving the problem of hybrid flow shop based on optimizing makespan of the jobs to be scheduled.

In order to schedule jobs on parallel identical machines, the use of Time Petri Net based approach has also been investigated [26] while minimizing the makespan and balancing the load among the machines

Li et al. [27] used discrete multi-objective Artificial Bee Colony (ABC) to optimize makespan, the total workload of machines and the workload of the critical machine. They investigated the impact of schedules on maintenance activities. They used efficient initialization scheme and optimal Pareto front for obtaining efficient schedules for the jobs under consideration.

Motivated by the existing works on the use of nature-inspired algorithms for job scheduling, we investigated the application of nature-inspired Black Hole algorithm for the cause of job scheduling on parallel machines while optimizing Tmax and WFT.

• n: Number of jobs to be scheduled

• m: Number of potential parallel machines

• i:    Job under consideration

di: Due date of the ith job where i =1,2,,

• j:    Order of processing of i^th job on a machine, where

j =1, 2,,n

• k:    Machine to which a job has been allocated, where

k = 1,2,,m pi: Processing time of ith job wi: Weightage of ith job. It may indicate priority or importance of the job.

aik: Time at which machine k is allocated to ith job ci: Time of completion of ith job

Ti: Tardiness of i^th job

• A. Objective/Fitness Function

Maximum Tardiness (T max ) is the tolerance time up to which tardy job is permitted by the system.

T__ = m max T , where i =1 to n max          i

• III. Description of Job Scheduling Problem

The problem of scheduling multiple jobs on parallel potential machines for optimizing maximum tardiness and weighted flow time is one of the important problems that have been encountered by engineers time and again.

In order to describe the problem, let there be n jobs that can work independent of each other on m potential parallel machines. Each job has a due date, processing time and weight (or priority). All jobs are available at time zero. Further it is also presumed that a job cannot pre-empt other job at any point of time. The problem is to schedule given n jobs on m machines in such a way that T_max and WFT are minimized. The number of possible combinations of jobs (to formulate a schedule) that could be investigated is exponentially large and solution of such a problem is NP-hard [23]. Sharma et al. [28] proposed a heuristic that is able to solve this NP-hard problem. But as the size of problem increases, the efficiency and effectiveness of this approach reduces. As mentioned above, nature inspired algorithms have the capability to solve such large sized problems. The following assumptions, notations and decision variables have been drawn for the formulation of the problem.

Assumptions: The problem draws following assumption.

• •    A job could be processed on any machine.

• •    All jobs are available at time zero.

• •    Jobs can execute independent of each other.

• •    A job could not pre-empt any other job.

• •    All the machines are always available.

Notations: Following notations are used for the formulation of problem of job scheduling on parallel machines.

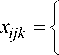
WFT= Sum of weighted completion times of the jobs

n

= Ё wici i =1

Decision Variables,

• 1,    if job i is allocated to machine k on postion j

• 0, otherewise

• 1, if job i is assigned to machine k

• 0, otherewise

  
  
  

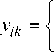
• [ 1,if job r immediately follows job i on machine k zirk = 1

[0,otherwise

It could be deduced that zirk=1 if xjk = 1 and xr(j+1)k = 1

• B.    Mathematical Formulation

The mathematical formulation for the given problem is as follows:

Minimise: Tmax=max Ti mnn

Minimise WFT=Min( Ё Ё Ё Xy^ * w i * c i ) k = 1 j = 1 i = 1 ^J

The constraints followed while scheduling jobs are described below.

T max is greater than equal to difference in completion time and due date for all the jobs.

T max ^ c i - d i , ^{V i}

All i jobs have been allocated to a machine k at some position j .

nmn

XXX xnk = n i I k I j I j

Allocation time of process r is equal to completion time of process i provided r follows i on machine k .

a rk = z irk * c i

Variables are either 0 or 1 (binary).

x ijk , y ik , z irk ^e{ 0,^{1 }}

Job i is assigned to only one machine and that too only once.

m

X y ik = 1 where i = 1,2,, n

• C.    Application

One of the possible applications of the problem under consideration is scheduling of large number of processes on multiple processors by the operating system. In such a system, numbers of processors (CPU) (as machines) are available all the time in parallel and number of processes (jobs) are to be scheduled on these processors. Each of the process (job) has its own processing time and priority. The processes are to be scheduled on available parallel processors such that there is minimum tardiness as well as minimum weighted flow time for the processes. This could lead to increase in the throughput rate. Further, use of parallel processors enhances production as the work does not stop when some processors fail or maintenance occurs.

• IV. Job Scheduling on Parallel Machines using Black Hole Algorithm

Algorithms imitating processes found in nature are called nature-inspired algorithms. It has been a field of inclination for people in scientific and engineering studies in recent years. In actual engineering problems, different objectives often conflict with each other, and hence obtaining an optimal result is very difficult. Nature-inspired algorithms are found to be very efficient in solving such complex problems.

We propose to apply multi-objective Black Hole algorithm to the problem of job shop scheduling on parallel machines taking into consideration the objectives namely T max and WFT.

This section describes our adaptation of nature-inspired algorithms to the problem of job scheduling on parallel machines. This adaptation includes: representation of the solutions and the generation of the initial population; evaluation of individuals using multiple objectives namely Tmax and WFT; selection of the individuals from one generation to another; generation of new individuals; bringing algorithm out of local optima using genetic operators (to explore the search space in a better way); augmenting auxiliary archive to maintain non-dominated Pareto front for future considerations.

• A.    Solution Representation / Problem Encoding

The meta-heuristic algorithms proposed in this paper need appropriate encoding of the problem. It is observed that the encoding of the population has an impact on the quality of results generated by a meta-heuristic algorithm. In this proposed work, we encoded population as individuals made of floating point numbers. Size of each individual is equal to the number of jobs to be scheduled. Each position in an individual is represented by a decimal number having an integer part to indicate the machine number to which job has been allocated and a decimal part to indicate the order in which this job is allocated to that machine. As an example, let there be 5 jobs to be scheduled on two parallel machines. One of the individuals in the population is encoded as

Job id        1        2           3        4        5

Individual     2.01      1.02     2.02      1.01      2.03

This encoded individual has five positions. For job 1, the value of allele is 2.01. It means job1 is allocated to Machine 2 at the front followed by job 3 with allele value 2.02.

• B.    Generation of Candidate Population

To generate the population, following steps are followed.

//In order to find the order of allocation of jobs on machine k , create permutation of jobs allocated to the machine k .

Index=Permutation(Y p )

//Jobs are allocated to machine k on the basis of their permutation (order in index). This value is used as mantissa for the floating type decision variables (as discussed above) and the resulting decision variable becomes

X p . j and x jk = ¹

• C.    Proposed Job Scheduling Algorithms

This section proposes four stepwise algorithms that are based on the chosen nature-inspired Black Hole algorithm, and its hybrids with GA and auxiliary archive. All these algorithms are used to solve the problem of job scheduling on parallel machines. The first algorithm is based on multi-objective formulation of Black Hole algorithm based on weighted objectives. T max and WFT have been used as objective to be optimized. The second algorithm is developed by hybridising the first algorithm with GA. The third algorithm uses auxiliary archive to store non-dominated Pareto front. The fourth algorithm has been developed by adding Genetic algorithm to the third algorithm. Following section describes the proposed algorithms in detail.

Multi-Objective Weighted Black Hole Algorithm (MOWBH) :

In this algorithm, Black Hole algorithm is implemented as multi-objective approach using weighted objective sum technique. In this technique, all h objectives under consideration are combined to make a single objective (F) using (2) [29].

Each of the objectives is assigned random weights such that hh w„ > 0, Z w„ = 1 and F= Z w„ * L       (2)

g     g=1 g             g=1 g g g indicates the objective under consideration, g varies from 1 to h (number of ojectives to be optmized), wg is the random weight allocated to gth objective, fg is the value of gth objective and F is the combined single objective calculated from all the objectives in the problem under consideration.

The basic structure of this algorithm is as discussed below.

Step 1 [Initialize population]: Encode and initialise the population of candidate solutions as discussed above. The detail of common parameters to be used in the implementation of these algorithms is given in Table 1. These values are obtained by manual tuning after repeated executions of the algorithms. Evaluate fitness of each candidate in the population on the basis of combined weighted objective F (2). Designate the solution with least value of F as Black Hole (XBH).

Table 1. Common control parameters for Black Hole algorithm for job scheduling on Parallel machines

Parameter	Value	Description
Number of variables to be optimised (n)	Number of jobs to be sequenced	Number of decision variables in the individual is equal to the number of jobs to be sequenced.
Population size	5 times the number of jobs to be scheduled	With increase in number of jobs to be scheduled, population size increases.
Population	Candidate  schedules for the jobs	Randomly generated.
Generations	•    15    times    the number of jobs to be scheduled  (n) and  number  of machines  to  be used            in parallel(m)= 15*m*n Or •    When solution does not change for 400 consecutive generations	Stopping criteria
Objective functions	T max and WFT	Weighted sum of objectives (in MOWBH and MOWBHGA) or Pareto front of possible nondominated individuals (in MOBH and MOBHGA) is created using these objectives depending on the algorithm used.
Lower bound  for decision variables (X i min)	1.1	Job is allocated to machine number 1 before any other job.
Upper bound  for decision variables ( X m i ax )	m.n	Job is allocated to last machine m and in worst case all n jobs are allocated to this last machine. In this way, order of job will be n .
Size     of REP	1%   of   size   of population	To keep track of best (nondominating) solutions

Repeat Steps 2-4 until stopping criteria is met (as indicated in Table 1).

Step 2 [Identify new possible solutions]: For each iteration t, identify new location ( X_p(t+1) ) for each job sequence ( X_p(t) ) by using (3)

X_p ( t + 1) = X p ( t ) + rand *( Xbh - X p ( t )) (3)

Step 3 [Search for a better solution]: Calculate the fitness of this new solution Xp(t+1) by using (2). If new candidate solution is better than the current candidate solution, then replace the current solution with this new solution else ignores it. This step is required to locally search for better sequence. It moves the current candidate randomly in search for a better solution.

If the new solution is better the current Black Hole (X BH ), then designate this new solution as new Black Hole.

Step 4 [Discard vanished solution]: Calculate the radius of event of horizon of the Black Hole job sequence by using (4).

R = p F BH- (4)

E F p p = 1

where F BH is the fitness for Black Hole job sequence and F p is the fitness of p^th job sequences calculated using weighted fitness function calculated using (2). Pop is the size of population under consideration (as mentioned in Table 1). If a star enters this event horizon, it is absorbed by the Black Hole.

If ( F p - F BH < R ), the job sequence is discarded as it is regarded to be entered in event horizon of Black Hole and is thus vanished.

Generate new job sequence to balance the size of population.

Step 5 [Output] : Output the best job sequence.

Black Hole algorithm works to find optimized results but might get stuck at local optima. GA has an inherent capability of performing a wider search ability due to the use of crossover and mutation operators. The crossover operator helps in swapping of information between two candidate solutions which increases the ability to investigate new solution areas, whereas the mutation operator increases the diversity of the population and helps to avoid the local optima.

Multi-Objective Weighted Black Hole Genetic Algorithm (MOWBHGA) :

In this algorithm, genetic phase has been appended to MOWBH after Step 4 to develop MOWBHGA. Combined fitness function (2) used in MOWBH is taken as the objective to be optimized.

New Step 5 (Genetic Phase) is described as below:

Step 5.1 [Input] : Take population of candidate job sequences from Step 4 of MOWBH as input population of chromosomes. Calculate fitness of each solution using combined fitness function F (using (2)).

Step 5.2 [Selection] : Select two parent chromosomes (possible job sequence) from the population using tournament selection on the basis of their fitness calculated in Step 5.1.

Step 5.3 [Crossover] : Cross the parents selected in Step 5.2 to create new children with crossover probability of 0.6. Arithmetic crossover operator has been used for this purpose. The crossover probability can be obtained by repeated executions of the algorithm and has been tested manually.

Step 5.4 [Mutation] : Mutate new child at random positions (job) in the chromosome with mutation probability of 0.2.

Step 5.5 [Replace] : If this new offspring is better than the parents (lesser fitness value) then accept it. The population thus obtained is used by next iteration of Black Hole algorithm. The parameters to be used to implement GA are shown in Table 2. These parameters are obtained by manual tuning and repeated executions of the algorithms under consideration.

Table 2. Control parameters for GA

Parameter	Value	Description
Selection algorithm	Tournament (Size 2)	Candidate sequences Parent1 and Parent2 are selected for crossover using this method. It could be efficiently coded, works on parallel architectures and allows the selection pressure to be easily adjusted
Crossover function	Arithmetic	Child=R1 * Parent1+ R2 * Parent2 Where R1,R2 are independent random numbers between 0 and 1 It always produces feasible offspring for a convex solution space. Set crossover fraction to 0.6.
Mutation function	Uniform	Set mutation rate to 0.02. Manually tested to give best result.
Objective functions	T max and WFT	Weighted sum of objectives (in Proposed Algorithm 2) or Pareto front of possible non-dominated individuals (in Proposed Algorithm 4) is created using these objectives depending on the algorithm used.

Multi-Objective Black Hole Algorithm (MOBH):

The algorithm discussed above have a serious shortcoming. They return the single objective and are highly dependent on the weights. At the same time allocation of weights to the individual objective is difficult.

In case of random selection of weights, the output is highly unpredictable. So, we investigated the use of Pareto optimization [30] (resulting in solutions in the form of Pareto front) for optimization of job schedule using Black Hole algorithms discussed above. In order to store this Pareto front, an auxiliary archive and hypercubes are used to select best solutions (MOBH) for each iteration of the algorithm.

Step wise implementation of this algorithm is discussed below.

Step 1 [Initialize population] : Encode and initialize the populations of individuals as discussed above. The detail of common parameters to be used in the implementation of these algorithms is given in Table 1.

Step 1.1: Evaluate fitness of each candidate in the population using objective functions namely T max and WFT.

Step 1.2: Store the job sequence that represent nondominated vectors in the temporary repository also called auxiliary archive and is named REP.

Step 1.3: Generate hyper-cubes of the search space explored so far, and locate the sequence using these hyper-cubes as a coordinate system where coordinates of each job sequence are defined according to the values of its objective functions [31].

Step 1.4: Select the best solution achieved so far and designate it as Black Hole (X BH ).

Repeat Steps 2 to 4 for a predefined number of iterations (as shown in Table 1).

Step 2 [Identify new possible solution] : For each iteration t, identify new location ( X_p(t+1) ) for each job sequence ( X_p(t) ) by using (3).

Each of the i^th decision variables ( ) of the current candidate solution ( p ) is kept within permitted upper and lower bound (as shown in Table 1) for the job sequence under consideration.

Step 3 [Search for a better solution] : Calculate the fitness of this new solution taking into consideration the non-dominance of the job sequences. If this new solution dominates the current candidate solution, then replace candidate solution with this better new solution. This step is required to search locally for a better job sequence. It moves the current candidate randomly in search for a better solution.

If the new solution dominates the current Black Hole ( X_BH ) then designate this new solution as new Black Hole.

Step 4 [Discard vanished solution]: For calculating radius of event of horizon (of Black Hole) in nondominated Pareto front, calculate components of radius on the basis of objectives calculated using (5).

For all h objectives

Multi-Objective Black Hole Genetic Algorithm (MOBHGA) :

Similar to shortcoming of MOWBH algorithm, MOBH algorithm might get stuck at local optima. Due to the reasons mentioned for MOWBHGA, GA is appended as Step 5 in MOBH to developed MOBHGA algorithm.

New Step 5 (Genetic Phase) is described as below:

Step 5.1 [Input] : Take the population of candidate job sequence from the nature-inspired algorithm under consideration as input population of chromosomes. Calculate the fitness of each solution using the nondominance approach on the basis of objectives namely T max and WFT.

Step 5.2 [Selection] : Select two parent chromosomes (possible job sequences) from the population using tournament selection on the basis of their fitness calculated in Step 5.1.

Step 5.3 [Crossover]: Cross the parents selected in Step 5.2 to create new children with crossover probability of 0.6. Arithmetic crossover operator has been used for this purpose. The crossover probability is obtained by repeated executions of the algorithm, and has been tested manually.

Step 5.4 [Mutation]: Mutate new child at random positions (assignment of a job to a machine is changed) in the chromosome with mutation probability of 0.2.

Step 5.5 [Replace]: If this new offspring is better than the parents (non-dominating), then accept it.

The parameters to be used in this phase are shown in Table 2.

R ( h) =

f_BH ( h )

pop

I f p ( h ) p = 1

where f_BH is the fitness value of the Black Hole job sequence and f_p(h) is the fitness value of the h^th objective of p^th job sequence. For the problem of job sequence under consideration, the number of objectives ( h ) is equal to 2.

For each individual in the population, if difference in fitness value of every objective function and Black Hole dominates corresponding component of R ( f p (h)-f BH dominates R(h) ) calculated in (5), the job sequence is discarded as it is regarded to be entered in event horizon of Black Hole and is thus vanished.

Generate new job sequence to balance the size of population. Update REP as well as the geographical representation of job sequences within hyper-cubes [32] by inserting all the currently non-dominated locations into the auxiliary archive (REP) and eliminating dominated individuals.

Step 5 [Output]: REP contains the possible Pareto front i.e. the possible non-dominated solutions as output.

• V.    Experimental Setup

This section describes the experimental set up for implementation of proposed algorithm and their analysis. The comparison of the proposed nature-inspired multiobjective Black Hole algorithms for job shop scheduling on parallel machines has been done with some of the already known search based algorithms: MOGA [33], NSGA-II [34] and MOPSO [31] algorithm.

Table 3. Detail of parameters required to generate random samples.

Parameter	Value
Number of Jobs ( n )	40,60
Number  of Machines ( m )	2,3,6
Upper   bound    for processing time( X m i ax )	80
Lower   bound   for processing time( Ximin )	20
Weight/Priority of the job ( w i )	Randomly generated numbers between lower bound and upper bound
Due date for the job ( d i )	Randomly generated and greater than processing time for the job

• A.    Samples Under Study

All algorithms considered in this paper are implemented in MATLAB 8 [35]. The multi-objective algorithms discussed in this paper are applied on samples generated randomly in MATLAB. The number of parallel machines to be used for scheduling is taken as 2, 3 or 6. The upper and lower bound along with other details required for generating random samples are given in Table 3.

The algorithms under consideration are search based and are highly randomized, so these are repeated 30 times and best job sequence is taken as the output.

• B.    Assessment Criteria

In order to assess the quality of job sequence obtained by the application of proposed algorithms, Total Cost (sum of T max and WFT), Pareto front (T max vs WFT) and evolution of Total Cost with number of generations have been used as assessment criteria.

• C.    Total Cost of Job Sequence as Assessment Criteria

In order to evaluate the quality of resulting job sequences, objectives T_max and WFT are used. All algorithms considered in this paper are multi-objective in nature, so they lead to Pareto-front as an output. Since Pareto front consists of non-dominated possible solutions, where none of the solutions in Pareto front dominates others, we used Total Cost (sum of T max and WFT) of the solution as criteria to assess the quality of job sequence. Lower the value of this cost better is the job sequence solution.

• D.    Pareto Front as Assessment Criteria

In order to compare the kind of non-dominated solution thus obtained, we used Pareto front obtained by the application of all algorithms under consideration. The Pareto front is obtained by plotting Tmax on X-axis and WFT on Y-axis.

• E.    Evolution of Objectives with Generations as Assessment Criteria

The change in the values of objectives with generations/iterations are used to compare the stability (number of generation it needs to give a constant value for the objective) of the algorithms being used.

• F.    Statistical Validation

Since meta-heuristic algorithms considered in this paper are search based and are highly randomized optimizers, they may provide different results for the same problem instance from one execution to another. Hence, the algorithms are run 30 times.

In order to statistically validate the significantly better results obtained by the use of GA (as one of the phases of the algorithms) as well as the use of auxiliary archive, the Wilcoxon rank sum test [36] with a 95% confidence level (α = 5%) has been conducted.

The tests have been conducted between MOWBH and MOWBHGA; MOBH and MOBHGA; MOBHGA and

MOGA; MOBHGA and NSGA-II; MOBHGA and MOPSO.

The null and alternative hypothesis for the same is as discussed below.

Null hypothesis H0: The obtained results by the application of algorithms under consideration are samples from continuous distributions with equal medians.

Alternative Hypothesis H1: The obtained results by the application of algorithms under consideration are not samples from continuous distributions with equal medians.

The test returns h-value and p-value. The h-value indicates whether the null hypothesis H0 is accepted or rejected. The p-value indicates the probability of rejecting the null hypothesis H0 while it is true (type I error). A p-value that is less than or equal to α (≤ 0.05) means H1 is accepted. The corresponding h-value is 1. If the p-value is strictly greater than α (> 0.05), Alternative Hypothesis H1 is rejected and Null Hypothesis H0 is accepted. The corresponding h-value is 0.

• VI.    Experiments Results

The multi-objective algorithms discussed in this paper are applied on samples of varied sizes generated randomly on the basis of parameters shown in Table 3. The quality of resulting job sequences are assessed on the basis of criteria as discussed below.

• A.    Total Cost of Job Sequence as Assessment Criteria

Table 4 shows the Total Cost of non-dominated job sequence with lowest total of T max and WFT criteria. The job sequences are obtained by the application of MOWBH, MOWBHGA, MOBH and MOBHGA for all the samples under consideration.

In order to further compare our findings, we plot the Total Cost (T_max and WFT) obtained by the application of all the algorithms and for all the samples. Fig. 1 plots Total Cost obtained by application of MOWBH and MOWBHGA algorithms for all the samples under consideration. Fig. 2 plots Total Cost obtained by the application of MOBH and MOBHGA algorithms for all the samples under consideration.

By close evaluation of Tables 4 and Fig. 1, it is observed that the hybrid algorithm obtained by the application of GA (MOWBHGA) outperforms MOWBH. Similar improvements in quality of job schedules have been observed (in terms of Total Cost) by using GA with MOBH (to obtain MOBHGA) as observed by analysis of Table 4 and Fig. 2. This improvement in efficiency of MOWBH and MOBH is due to the use of GA which tends to bring these algorithms out of local optima and hence directs the search towards global optimization.

Fig. 3 displays Total Cost obtained by the application of MOWBHGA, MOBHGA and compares the results to that of existing MOGA, NSGA-II and MOPSO algorithms. Analysis of Table 4 and Fig. 3 reveals that MOBHGA that is based on the use of auxiliary archive and GA perform better than MOWBHGA.

Further analysis shows that MOBHGA outperforms all other existing algorithms (MOGA, NSGA-II and MOPSO) in terms of Total Cost of the job sequence thus obtained.

• B.    Pareto Front as Assessment Criteria

Fig. 4-9 plots Objective 1 (T max ) on X-axis and Objective 2 (WFT) on Y-axis (for each algorithm) for all the samples under consideration. It shows the kind of solution space thus obtained. In a multi-objective environment, it is called Pareto front which shows the set of non-dominated solutions space.

On analysis of Fig. 4-9, it is deduced that MOGA results in dense Pareto front as compared to the proposed algorithms. But if we select the solution with least values of both T max and WFT, it can be easily seen that MOBHGA outperforms other algorithms including MOGA.

• C.    Evolution of Objectives with Generation as Assessment Criteria

Fig. 10-15 plot the fitness function ( Total Cost ) and generations (iterations) obtained by the application of all the proposed algorithms for all the samples under consideration. If we analyse this evolution, it is observed that although MOGA gets stable in lesser iterations as compared to other algorithms, MOBHGA is found to result in better optimizations in most of the cases (except for sample with 40 jobs to be scheduled on 2 machines in which MOGA results in Total Cost comparable to MOBHGA).

For 4 out of 6 samples, MOWBHGA is found to optimize better than MOGA.

MOWBHGA and MOBHGA are found to get stable in lesser iterations as compare to NSGA-II and MOPSO in all the cases.

• D.    Statistical Test

Wilcoxon rank sum testhas been conducted between MOWBH-MOWBHGA; MOBH-MOBHGA; MOBHGA-MOGA; MOBHGA-NSGA-II and MOBHGA-MOPSO (for all the samples under study). The results thus obtained are shown in Table 5.

On analysing Tables 4, it is observed that adding GA to MOWBH and MOBH improves the process of job scheduling. Values of Wilcoxon rank sum test further validates the findings and justify the observations that in most of the cases, h-values corresponding to Wilcoxon test between MOWBH-MOWBHGA and MOBH-MOBHGA are 1 which indicates that the samples are from distributions having different medians. It means the sequences obtained by the application of GA based algorithms are significantly better. Analysis of Table 4 reveals that MOBHGA leads to best job sequences for the problem under consideration. Table 5 reveals the difference to be significant as h-value obtained as a result of Wilcoxon rank sum test between MOWBHGA and MOBHGA is 1 in all the cases. So, further Wilcoxon rank sum tests have been performed between MOBHGA and state of art optimization algorithms.

If we analyse the results of test between MOBHGA-MOGA; MOBHGA-NSGA-II and MOBHGA-MOPSO, it is observed that in case of MOPSO, the h-value is 1 in all the cases, in case of NSGA-II, the h-value is 1 in all the cases except for 40 jobs to be scheduled on 6 machines; whereas in case of MOGA, the values are 1 in most of the cases except for 40 jobs to be scheduled on 3 machines and for 60 jobs to be scheduled on 2 machines. So, it is statistically validated that MOBHGA leads to optimum job sequences as compared to other algorithms in most of the cases.

Table 4. Solution with least Total Cost for randomly generated samples

Algorithm			MOWBH	MOWBHGA	MOBH	MOBHGA	MOGA	NAGA-II	MOPSO
Number of Machines	Number of Jobs	Value    of Objective
2	40	T max	1016	979	1005	970	963	985	1002
		WFT	488.11	351.98	407.56	350.27	356.72	365.16	438.12
		Total Cost	1504.11	13330	1412.56	1320.27	1320.72	1350.16	1440.12
	60	T max	1514	1500	1499	1489	1499	1500	1505
		WFT	751.12	510.94	622.92	511.03	548.72	535	748.43
		Total Cost	2265.12	2010.94	2121.92	2000.03	2047.72	2035	2253.43
3	40	T max	649	580	659	574	630	610	650
		WFT	354.17	230.75	306.84	226.93	250.99	240.74	345.67
		Total Cost	1003.17	810.75	965.84	800.81	880.99	850.74	995.67
	60	T max	990	958	980	976	980	977	990
		WFT	542.27	360.43	429.07	328.07	403.62	387.14	550.77
		Total Cost	1532.27	1318.43	1409.07	1304.07	1383.62	1364.14	1540.77
6	40	T max	347	283	319	280	295	286	305
		WFT	191.71	158.54	162.44	150.81	170.15	157.19	195.31
		Total Cost	538.71	441.54	481.44	430.81	465.15	443.19	500.31
	60	T max	508	457	488	455	465	470	510
		WFT	266.85	225.35	210.98	214.18	214.67	261.03	322.63
		Total Cost	774.85	682.35	698.98	669.18	679.67	731.03	832.63

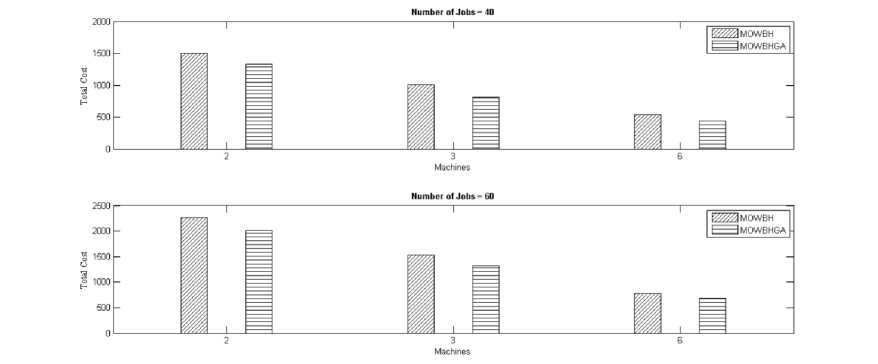
Fig.1. Best values obtained with 40 and 60 jobs scheduled on 2, 3 and 6 machines by MOWBH and MOWBHGA algorithms

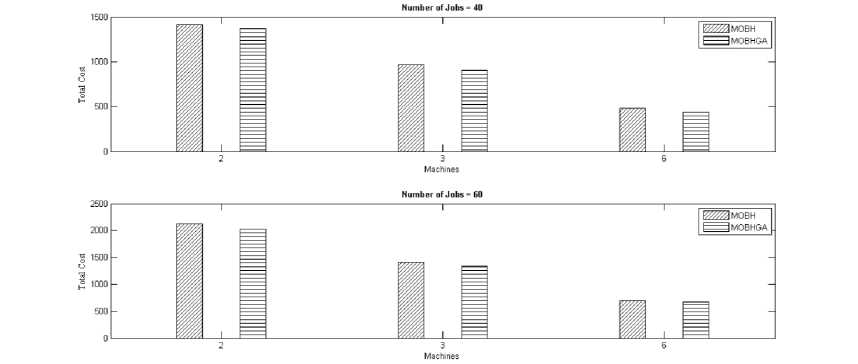
Fig.2. Best values obtained with 40 and 60 jobs scheduled on 2, 3 and 6 machines by MOBH and MOBHGA algorithms

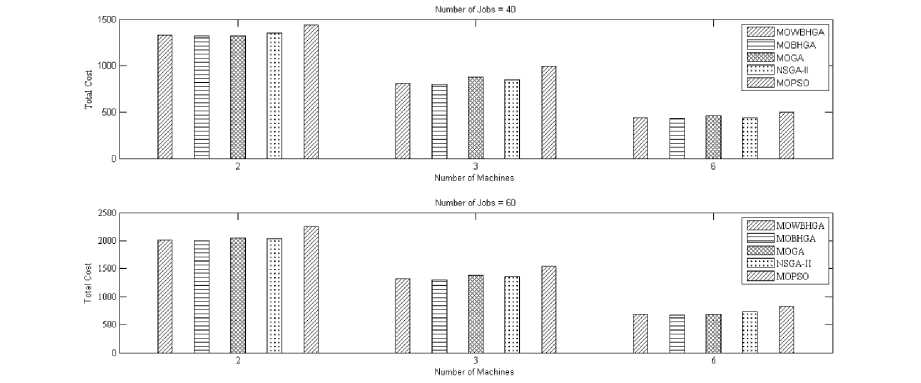
Fig.3. Best values obtained with 40 and 60 jobs scheduled on 2, 3 and 6 machines by MOWBHGA, MOBHGA, MOGA, NAGA-II, MOPSO algorithms

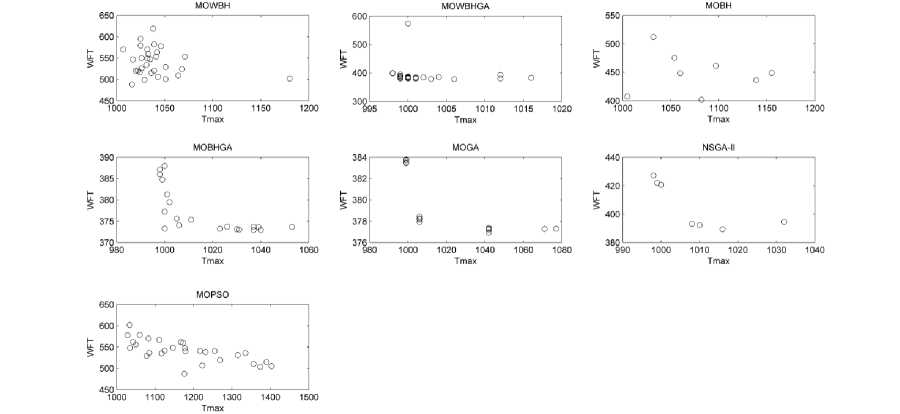
Fig.4. T max Vs WFT (Pareto Front) for all the algorithms for 40 jobs scheduled on 2 machines

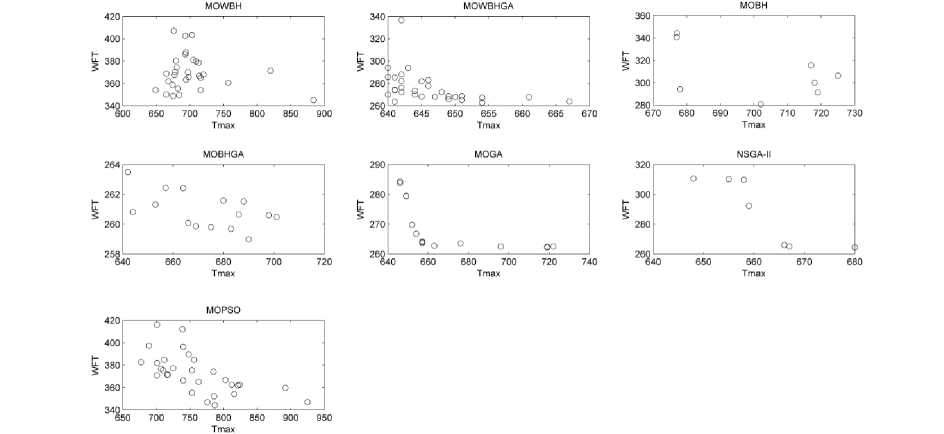
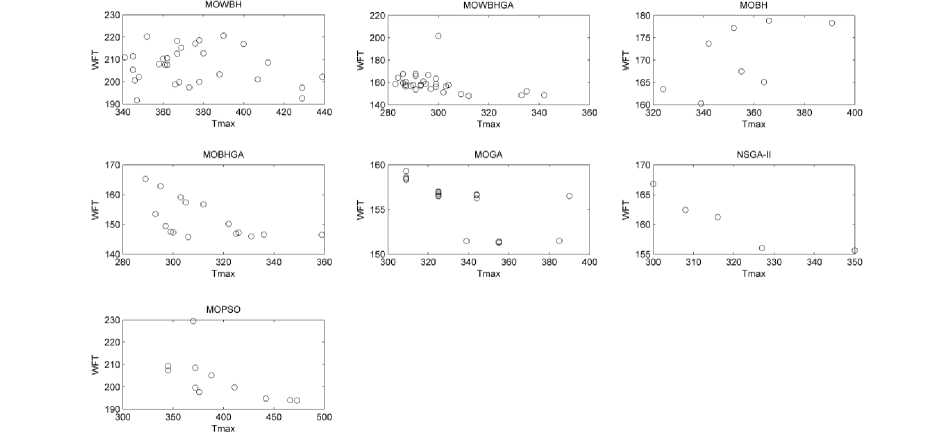
Fig.6. T max Vs WFT (Pareto Front) for all the algorithms for 40 jobs scheduled on 6 machines

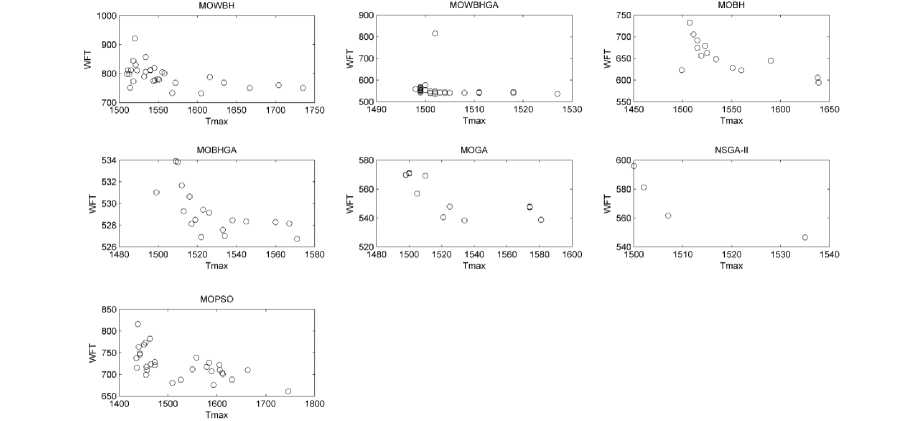
Fig.7. T max Vs WFT (Pareto Front) for all the algorithms for 60 jobs scheduled on 2 machines

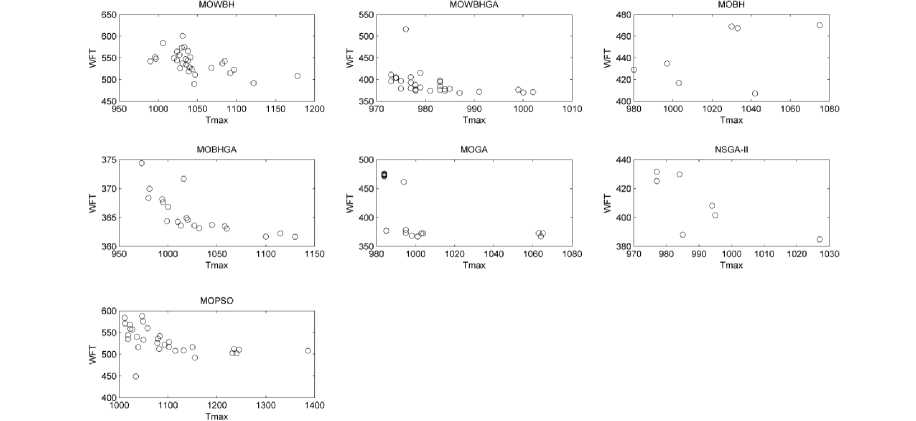
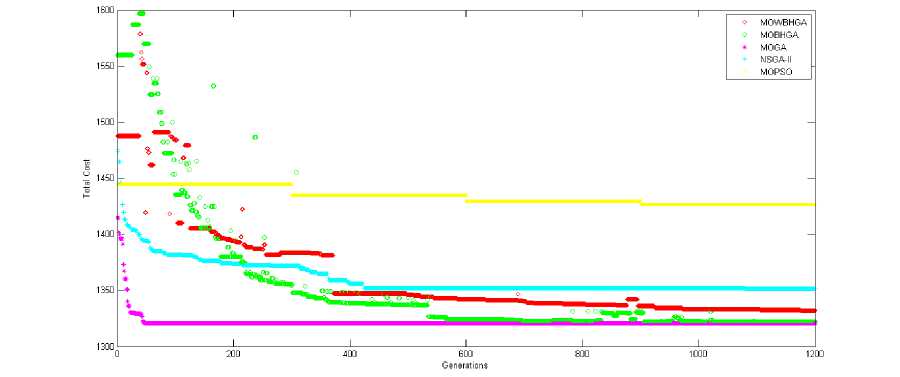
Fig.10. Evolution of Total Cost based on number of generations for 40 jobs scheduled on 2 machines

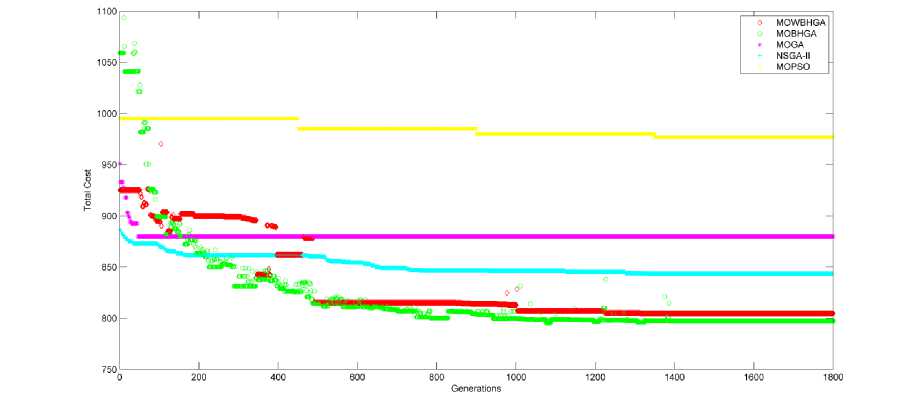
Fig.11. Evolution of Total Cost based on number of generations for 40 jobs scheduled on 3 machines

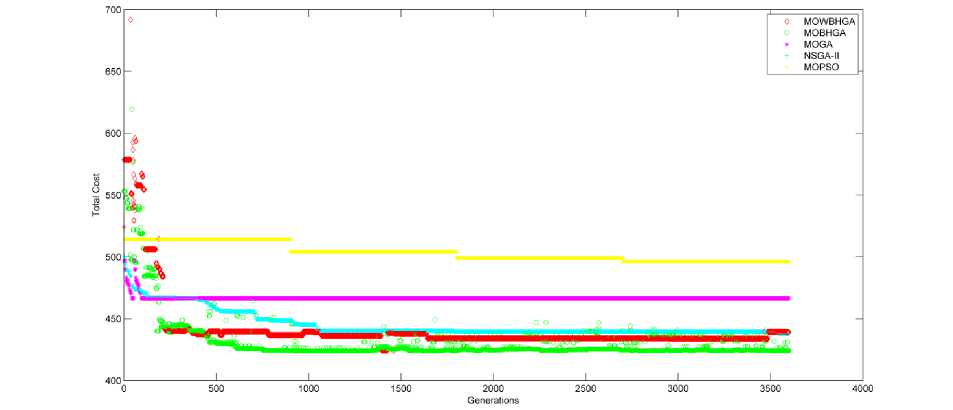
Fig.12. Evolution of Total Cost based on number of generations for 40 jobs scheduled on 6 machines

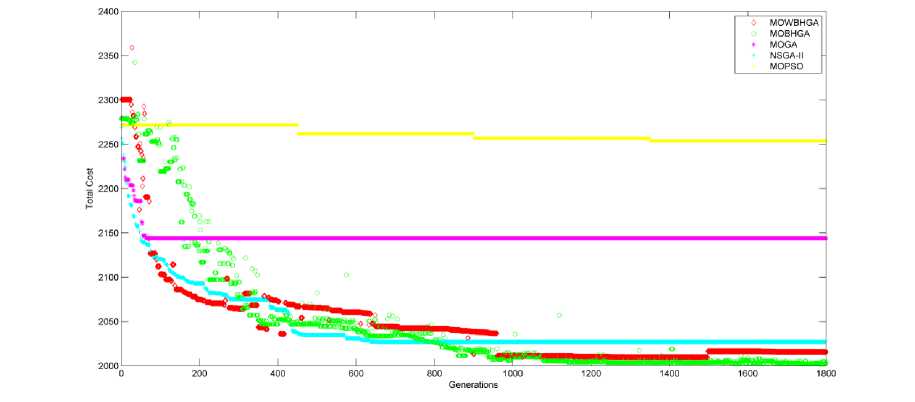
Fig.13. Evolution of Total Cost based on number of generations for 60 jobs scheduled on 2 machines

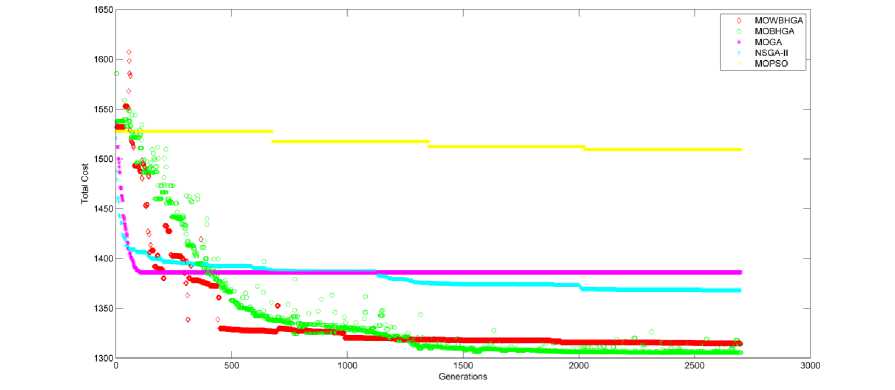
Fig.14. Evolution of Total Cost based on number of generations for 60 jobs scheduled on 3 machines

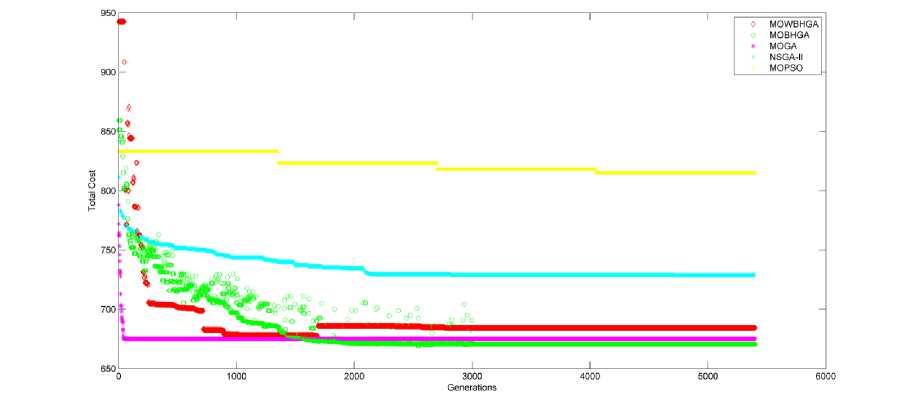
Fig.15. Evolution of Total Cost based on number of generations for 60 jobs scheduled on 6 machines

Table 5. Wilcoxon test between proposed and state of art algorithms

Algorithm	Test Value	Machines=2				Machines=3				Machines=6
		N=40		N=60		N=40		N=60		N=40		N=60
		Tmax	WFT	Tmax	WFT	Tmax	WFT	Tmax	WFT	Tmax	WFT	Tmax	WFT
MOWBH Vs MOWBHGA	h	1	1	1	1	1	1	1	1	1	1	1	1
	p	3.643e-011	3.474e-010	3.109e-010	3.4742 e-010	7.926 e-011	3.020 e-011	1.201 e-010	7.413 e-011	3.299 e-011	7.389 e-011	2.965 e-011	3.338 e-011
MOBH Vs MOBHGA	h	1	1	1	1	1	1	1	1	1	1	0	1
	p	9.185e-010	2.538e-011	0.012	2.3601 e-011	4.930 e-005	2.545 e-011	0.018	2.441 e-011	3.558 e-010	5.202 e-010	0.324	1.465 e-007
MOWBHGA Vs MOBHGA	h	1	1	1	1	1	1	1	1	1	1	1	1
	p	1.607e-004	1.280e-006	8.997e-011	3.8356 e-016	1.915 e-008	3.610 e-011	1.829 e-011	1.823 e-015	0.002	2.574 e-005	5.309 e-011	4.914 e-011
MOBHGA Vs MOGA	h	1	1	0	1	0	1	1	1	1	1	1	1
	p	2.082e-004	1.370e-016	0.843	2.2419 e-033	0.434	8.279 e-018	0.002	1.023 e-029	9.179 e-006	1.672 e-021	1.655 e-004	4.878 e-017
MOBHGA Vs NSGA-II	h	1	1	1	1	1	1	1	1	0	1	1	1
	p	3.665e-012	8.030e-039	4.056e-028	1.6082 e-038	0.003	1.168 e-028	6.127 e-005	1.148 e-038	0.077	3.402 e-026	6.111 e-004	2.231 e-038
MOBHGA Vs MOPSO	h	1	1	1	1	1	1	1	1	1	1	1	1
	p	6.756e-027	4.443e-031	1.052e-004	1.352 e-032	6.867 e-016	3.088 e-017	9.957 e-009	3.055 e-019	8.868 e-008	5.821 e-008	3.508 e-022	2.893 e-031

• E.    Summary of Results

By analysis of all the above assessment criteria, it is empirically evaluated that MOWBHGA performs better than MOWBH. Similar improvement has been encountered for MOBHGA which is optimizing better than MOBH.

It is empirically evident that MOBHGA performs better than other state of art algorithms: MOWBHGA, MOGA, NSGA-II and MOPSO.

The statistical test further validates the improvement to be significant.

• VII.    Threats to Validity

Threats to validity refer to the factors that can bias our empirical study. With respect to current research work, there are two kinds of threats; internal and external validity.

Internal validity refers to the biases in the results related to proposed algorithms. We take into consideration the internal threats to validity while tuning of the parameters. In order to mitigate this threat, we repeated the executions of algorithms and manually tuned the parameters involved.

External validity refers to the generalizations that are done beyond the samples used in empirical study. In this study, we mitigated external threat by performing experiments on randomly generated samples. For generalization of results, more experiments need to be performed.

• VIII.    Conclusions

Scheduling jobs on parallel machines, while taking care of maximum tardiness and weighted flow time, is one of the issues that has been encountered in various engineering and manufacturing problems and has found a large number of applications. A large number of heuristic and meta-heuristic techniques have been developed to solve this problem. In this paper, weighted objective multi-objective Black Hole algorithm along with its hybrid with GA has been proposed for solving such scheduling problems.

Further, multi-objective Black Hole is developed by using auxiliary archive (to keep track of non-dominated solutions) and GA. This algorithm yields appreciable results with a significant improvement in job scheduling process. The results are further verified empirically by performing numerical illustrations and Wilcoxon test.

The work can be further extended by experimenting with other novel nature-inspired algorithms such as Bat [14] and Firefly algorithms[11]. Other criteria such as number of tardy jobs, earliness, tardiness etc. could also be experimented as possible objectives for efficient scheduling of jobs on parallel machines.