Hybrid Flow Shop Scheduling Problem Using Artificial Immune System

Published Online September 2012 in MECS

In order to solve complex problems, ideas inspired from natural mechanisms have been exploited to develop heuristics inspired by nature. The artificial immune system (AIS) is a recent paradigm that attempts to capture interesting features of the natural immune system (NIS), such as memorization, pattern recognition, learning, combinatorial optimization, intrusion detection in computer networks, robotics, machine learning, etc...[6].

In this paper, an adaptation of this new technique to solve the hybrid flow shop scheduling problem is presented. In a hybrid flow shop (FSH), the machines are arranged in series in s stages and in each stage k (k = 1 ..., s) there are mk identical machines in parallel. Each job (Job) j (j = 1 ..., n) is processed by any one machine at each stage and has finite processing time (p1j, p2j... Pjs). Preemption is not allowed and each machine can process at most one operation at a time. The objective is to minimize the makespan (Cmax). The Hybrid Flow Shop problems have been proved to be NP-Hard [11] when the objective is to minimize the makespan in case of Max (M (1), M (2))> 1 where M (L) is the number of machines in stage L.

In this paper, we present an algorithm inspired by the vertebrate immune system, followed by an explanation of the mechanism of the vertebrate immune system has been the inspiration for our algorithm. We'll post the description of the algorithm and parameters. At the end we will discuss the results obtained by the AIS application for solving scheduling problems in production systems type FSH by varying different parameters.

• II.    Artificial Immune System (AIS)

• 2.1    Clonal Selection Principle [4]

The mechanisms of the natural immune system are very effective and can develop powerful computational tools. The algorithm presented is based on the principle of clonal selection principle and affinity maturation of the natural immune system.

When the body is exposed to an antigen, B lymphocytes (cells of the natural immune system) respond by producing antibodies. Each cell secretes a single type of antibody specific for the antigen. By binding to these antibodies (cell receptors) and with a signal from accessory cells T-helper, the antigen stimulates the B cell to proliferate (divide) and differentiate into cells secreting antibody called plasma cells. The process of proliferation (mitosis) generates the clone (cell or group of cells that are the daughter cells from a single cell). The rate of cell proliferation is directly proportional to the degree of affinity with the antigen. B lymphocytes, in addition to their differentiation into plasma cells, they differentiate into memory cells that will be selected to produce antibodies in the case of an attack by the same antigens. This property is not subsequently integrated into our algorithm and thus it will not be mentioned in our article.

The main properties of the clonal theory inspiration of the algorithm are:

• >    Proliferation and differentiation of cells on stimulation with antigen,

• >    Generation of new genetic change that gives new models of antibody through somatic mutation (a process called affinity maturation).

• >    Elimination of lymphocytes from the proliferation that has low affinity for antigen.

• 2.2    Affinity Maturation

Fig. 1 shows the principle of clonal selection [4].

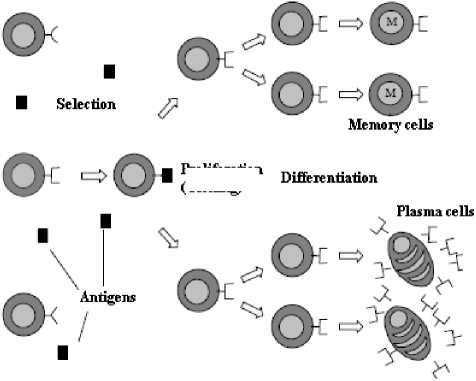
Fig. 1: Principle of clonal selection

Proliferation (Cloning)

Affinity maturation is the process of mutation and selection of offspring that better recognizes the antigen. The two basic mechanisms of affinity maturation are hypermutation and generation of receptors [4].

Somatic hypermutation is a random change (mutation) in the variable region genes of antibody molecules. These changes are mutational events that cause structural changes in the cell with the aim of increasing the affinity of the antibody with the antigen.

The rate of somatic hypermutation is inversely proportional to the affinity of the cell: the highest degree of affinity of the antibody with antigen minus the rate of mutation and vice versa. With this strategy the immune system keeps the cells of the offspring that have high affinity and guarantee a mutation rate for those with a low affinity for a better affinity.

The generation of receptor is due to the random nature of the process of somatic hypermutation. A large number of antibodies obtained are poor or not useful; these cells will be eliminated and replaced by other randomly generated. Therefore, the mutation to explore local areas and the generation of receptors avoids the problem of local optimum.

• III.    Proposed AIS Approach3.1    Algorithm

Representation: the "schedules" are represented by an integer string of length n (n jobs). The n elements of the chain are their processing order. The chains are permutations of various jobs.

These chains and most allocating jobs to different machines in each stage is an antibody. For our algorithm to find the solution, the algorithm is changing these antibodies. This development is based on two principles of natural immune system: clonal selection and affinity maturation.

The algorithm is as follows:

Create a population of antibody (A is the parameter of the population size of Antibody)

X = 0;

For each Generation Do

X = X +1

For each Antibody Do

Decode the antibodies in the antibody population;

Determine the makespan (affinity) of Antibodies;

Calculate the probability of selection (cloning rate);

Cloning (generate copies of antibodies)

For each generated clone Do :

Large mutation (generating a new solution):

Decoding the new solution:

Calculate the makespan of the new solution;

If makespan (new solution)

(Clone) then clone = new solution;

Else , do simple mutation (Pairwise interchange) (generating a new solution);

Decoding the new solution;

Calculate the makespan of the new solution;

If makespan (new solution) < makespan (clone) then clone = new solution;

Else , clone = clone;

End IF ;

End if ;

Antibody = clone;

If X = C (generation frequency of replacement) Then Eliminate B% number of antibodies in the population (the parameter B is the percentage of elimination of antibodies)

create B% new antibodies to replace those removed (B% pop.)

Replace those removed by the antibodies created;

X = 0;

End if;

Until a stop criterion = True;

• 3.2    Process of clonal selection in the algorithm

Each antibody is associated with a makespan (Cmax) that refers to its affinity value. This value is calculated by a function of affinity according to equation (1):

Affinity(z) =       1                    (1)

makespan(z)

where z is an antibody.

Following equation (1), we note that if the value of makespan is lower then the affinity value is high. In the algorithm the cloning of antibodies is directly proportional to their affinity value, which is the case for the natural immune system.

For the cloning process the procedure is the roulette wheel method [9]. In our study we used the Cmax as objective function, so we are faced with a minimization problem. The procedure gives more chance to antibodies with a lower Cmax for the selection and cloning. Will there consequently it more clones of antibodies for those with a lower Cmax than those with a higher Cmax in the new population generated clones.

The probability of selection for each antibody was calculated using the following procedure:

• >    For each antibody in the population, calculate the value of Cmax.

• >    Find the maximum value Cmax for all antibodies.

• >    For each antibody, calculate the fitness value: Fitness value = (Max (Cmax) +1) Cmax of the antibody.

• >    For each antibody, calculate its probability of selection is:

• 3.3    Process of affinity maturation in the algorithm3.3.1    The mutation

The fitness value of the antibody

The sum of fitness values for all

In the algorithm, the size of the population of antibodies is fixed and the size of all clones generated. The number of clones generated for each antibody varies according to its probability of selection. So the antibodies with a high probability of selection are more clones in all the clones generated. As the size of the population of antibodies is set then the antibodies with a higher Cmax may not have clones by antibodies against a lower Cmax may be several clones.

A mutation procedure is used in two phases where each clone generated undergo a large mutation in the first phase and a simple mutation by changing the position of two jobs (jobs) in the sequence in the second phase :

Large mutation: given a sequence s, let i is number of mutation (user-defined parameter), the neighbourhood of s is obtained by mutation of s i times.

If the value of Cmax of the sequence obtained (after large mutation) is less than that of the original (the clone generated), then the sequence obtained replaces the original sequence, if not, the sequence undergoes the other mutation (mutation simple Pairwise interchange), Fig.2 illustrates the process for i = 2:

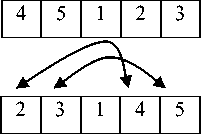
Fig. 2: The large mutation process

Simple Mutation (Pairwise interchange): given a sequence s, let i and j two positions in the sequence chosen randomly, the neighbourhood of s is obtained by the interchange of two positions of the sequence, the process is illustrated in Fig. 3:

A1

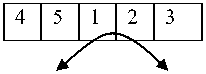
A1’

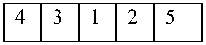
Fig. 3: The simple mutation process

If the value of Cmax of the mutated sequence (after transfer by the simple mutation) is less than that of the original sequence, then the sequence obtained replaces the original sequence.

In the case where the algorithm does not find the correct sequence after the two phases of the mutation, so it keeps the original sequence (clone generated). The large mutation allows finding the best solution in cases where the algorithm is still far better solutions, but where the algorithm has good solutions, the possibility of finding a better solution by applying a large mutation is low because it causes the loss of good partial sequences in the solution. To avoid this problem we applied the simple mutation in case the first mutation has not given the best solution.

• 3.3.2 . Receptor editing

After the cloning process and mutation a percentage of the population of antibodies (B%) are eliminated and replaced by other randomly generated. This mechanism is inspired by the mechanism called «Receptor editing "of the natural immune system.

This mechanism allows the exploration of new research space and avoids falling into the problem of local optimum. This process is applied after each generation C (C parameter defined by the user).

The clone set is accepted as an antibody population set for the next generation after these cloning selection, mutation and receptor editing processes. Thus, the clones, which have had the mutation process, are assigned as antibodies for the next generation. In the next generation the clones will be generated from these antibodies. This is succeeded by the statement: antibody = clone in the algorithm.

• IV.    Implementation and Testing4.1    Test Parameters

• 4.2    Problem of our application

The algorithm was tested on hybrid flow shop (FSH) type FSH4 (Characterized by a single stock in entry and between stages). The purpose of the tests is to study the influence of different user-defined parameters including the number of mutations for mutation Large

(Tmut), the replacement rate (B) and frequency of generation replacement (C).

For our tests we chose the Cmax (makespan) and our goal is to study at first the influence of different parameters to obtain the best solution is to tell the optimality and secondly the speed of convergence (CPU time necessary).

The problem is of type: FSH4 noted [11] by: FH3 (P4, P2, P3) | | C max (Fig. 4) is a hybrid flow shop with 3 stages and 4 machines on the first stage, 2 machines on the second stage and 3 machines on the third one:

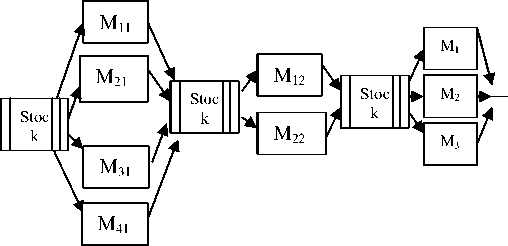
Fig. 4: Structure of a FSH4: FH3 (P4, P2, P3) | | Cmax

• 4.3    Analysis parameters4.3.1    Influence of the number of mutations (Tmut)

To study the influence of the number of mutations we fixed the population size P to 300 antibodies, the number of generations G to 300, the generation frequency to replace C to 100 and the replacement rate of antibody B to 20%. The parameter Tmut takes these values in {2, 3, 4, 5, 6, 7}.

Cmax is evaluated and the results are given by the Fig.5 for variation of the average Cmax with increasing rates of mutation Tmut and Fig.6 for the variation of the average CPU time with increasing rates of mutation Tmut.

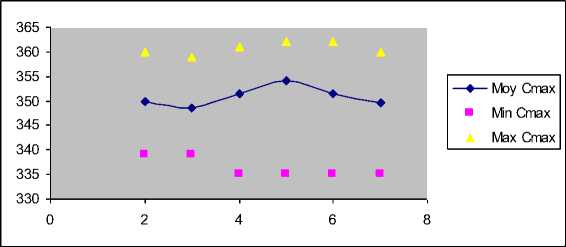
Fig.5: Change in mean Cmax with increasing rates of mutation (Tmut)

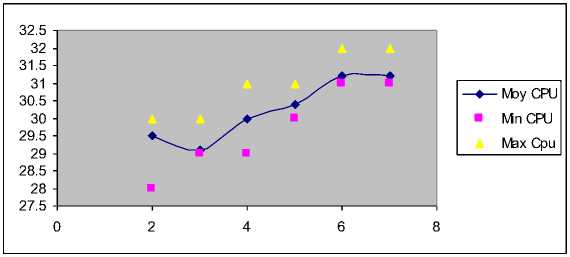
Fig.6: Variation of the average computer time (CPU) with increasing rates of mutation (Tmut)

The results represent the Minimum, Maximum and average Cmax after 10 executions of the algorithm for each value of the mutation rate. It is seen from Fig.5 that the number of mutations did not have much influence on the mean Cmax, but it affects the quality of solutions is obtained from Tmut = 4 we obtain good solutions to a value of 335. And as expected, we see from the Fig.6 an increase of time needed for convergence at each increase of Tmut.

• 4.3.2    Influence of replacement rate (B)

400.00 390.00 380.00 370.00 360.00 350.00 340.00 330.00 320.00

To study the influence of the replacement rate (B), we fixed the population size P to 300 antibodies, the number of generations G to 300, the frequency generation for the replacement C to 100 and the mutation rate Tmut to 2. The parameter B takes values in {10%, 20%, 30%, 50%, 75%, 100%}.

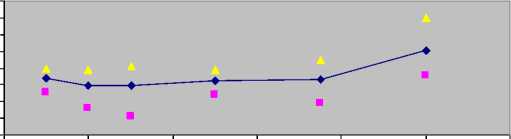
Cmax is evaluated and the results are shown in the Fig.7 for the variation of the average Cmax with increasing replacement rates (B) and Fig.8 for the variation of the average CPU time with increasing replacement rate (B).

0%       20%       40%       60%       80%       100%      120%

♦ Moy Cmax

■ Min Cmax

Max Cmax

Fig .7: Change in mean Cmax with increasing replacement rates (B)

50.00

40.00

30.00

20.00

10.00

0.00   -------------------1-------------------1-------------------1-------------------1-------------------1-----

0%    20%    40%    60%    80%    100%

—♦— Moy CPU

■ Min CPU

Max Cpu

120%

Fig.8: Variation of the average CPU time with increasing replacement rates (B)

The results represent the Minimum, Maximum and average Cmax and CPU time required after 10 executions of the algorithm for each value of the replacement rate B.

It is seen from the Fig.7 that the replacement rate affects the average Cmax in a way that is positive

(Cmax decreases) up to 50%, but from this value of B is finds that the average Cmax increases.

For the CPU time required is found from the Fig.8 that the time increases with increasing B.

• 4.3.3    Influence of generation frequency for the replacement C

To study the influence of frequency generation for the replacement C we fixed population size P to 300

antibodies, the number of generations G to 300 the number of mutations Tmut to 2 and the replacement rate B to 20%. The parameter C takes values in {20, 50, 70, 100, 150, 200, 300}. Cmax is evaluated and the results are given by the Fig.9 for the variation of the average Cmax with increasing frequency generation replacement and Fig.10 for the variation of the average

CPU time with increasing the frequency of generation

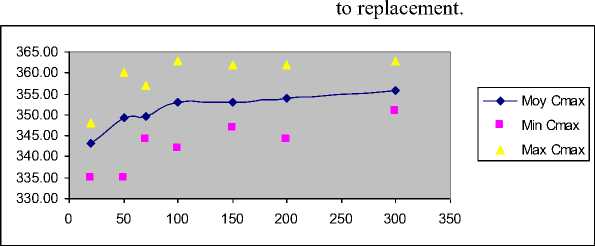
Fig.9: Change in mean Cmax with increasing frequency of generation to replacement

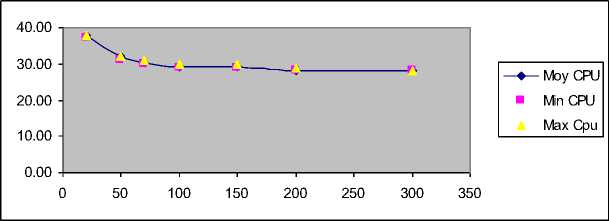
Fig.10: Variation of the average CPU time with increasing frequency of generation to replacement

The results represent the Minimum, Maximum and average Cmax and CPU time required after 10 executions of the algorithm for each value of the generation frequency to replacement C.

It is seen from the Fig.9 that increasing the frequency of generation to replacement for the slightly increased means Cmax.

For the CPU time required is found from the Fig.10 and as expected that the time decreases with increasing C. The results we have shown interest in the study of these parameters.

• V.    Conclusion

In this paper we presented the natural immune system inspired a new technique for solving problems. The various principles and mechanism inspired allowed us to propose an artificial immune algorithm to solve the problem of scheduling in production systems such as hybrid flow shop with the optimization criterion of makespan (Cmax).

The numerical results have shown the influence of various parameters on the performance of the algorithm in terms of solution quality and convergence time.

Our perspective will first make a comparative study with other methods such as genetic algorithms, the PSO ... and secondly to parallelize this algorithm in an attempt to obtain better results in acceptable time.