Hybrid Intelligent Routing in Wireless Mesh Networks: Soft Computing Based Approaches

Published Online December 2013 in MECS

Self configuring Wireless Mesh Networks (WMNs) are easily deployable, scalable, robust and cost effective wireless networks where nodes are having capability to automatically create and maintain mesh connectivity between them. Broadband home, community, neighborhood and enterprise networking are some of the applications of WMNs. The data packets, starting from the source node, hop from one node to another until it reaches the terminal node. Wireless Mesh Routers (WMRs) and Wireless Mesh Clients (WMCs)

are two types of nodes in WMNs. WMRs are capable for gateway/repeater functions as well as additional routing functions to maintain mesh networking. Based on the functionality of the nodes, the architecture of WMNs can be further categorized into three main groups namely: (1) Infrastructure/Backbone WMN: In infrastructure type WMNs mesh routers with gateway functionality form an infrastructure mesh for client nodes. (2) Client WMNs: Client WMNs provide peer-to-peer networks and client nodes perform routing along with self-configuration functions. (3) Hybrid WMNs: Hybrid Mesh is the combination of infrastructure and client meshing. Client nodes can access the network through mesh routers as well as directly meshing with other client nodes [1].

The parameters to analyze the performance of a WMN can be categorized as per flow, per node, per link, inter flow and network wide parameters. Commonly used performance metrics are Hop Count, Per-Hop Round Trip Time (RTT) [2] ; Per-Hop Packet Pair Delay and Expected Data Rate (EDR) [3]; Expected Transmission Count (ETX) [4], 2003; Expected Transmission on a Path (ETOP) [5]; Expected Transmission Time (ETT) and Weighted Cumulative ETT (WCETT) [6]; Effective Number of Transmissions (ENT) [7]; Bottleneck Link Capacity (BLC) [8]; Low Overhead Routing Metric [9]; Airtime Cost Routing Metric [10] etc. Hop Count Metric is the simplest one however; in most cases the minimum hop-count is not enough for a routing protocol to achieve good performance. Other routing metrics are critically affected by high overhead, low performance, high complexity or in-appropriate load balancing. The impact of performance metrics on a routing algorithm is discussed by Draves et al. [6].

It is required that routing policies must work in a decentralized, self-organizing and self configuring way while optimizing network resource utilization and fulfilling QoS requirements [11,12]. Due to complexities and constraints in exact reasoning based routing in dynamic wireless networks, there is a paradigm shift towards nature inspired soft computing based techniques. A fuzzy link cost based approach to achieve Quality of Service (QoS) and Quality of Experience (QoE) in WMNs is proposed by Gomes et al.[13]. A Genetic Algorithm (GA) based dynamic shortest path routing approach was proposed by Yang et al.[14]. Soft computing techniques i.e. GA and Neural Networks approach was applied to optimize Quality of Service (QoS) parameters for channel allocation in cellular networks[15]. A hybrid combination of Multi Objective Particle Swarm Optimization (MOPSO) and GA is proposed by Benyamina et al. to optimize the performance of WMNs [16]. A detailed description of various nature inspired meta-heuristic algorithms including ACO, Bee Algorithm, Bat Algorithm, Cuckoo Search, Firefly Algorithm, Particle Swarm optimization (PSO) etc. is presented by Yang [17]. An Ant Colony Optimization (ACO) based approach for routing in Mobile Ad hoc Networks (MANETS) is shown by Caro et al.[18]. An insect society collective behavior based routing for next generation networks was reported by Farooq and Di Caro [19].

Inspired by the soft computing approaches, this paper first proposes a fuzzy logic based hybrid performance metric consisting of throughput, delay, jitter of the link and residual energy of the node. Based upon these parameters this fuzzy module evaluates the Integrated Link Cost (ILC) for the corresponding link which is considered as the distance between adjacent nodes. Secondly two soft computing based routing strategies are proposed and implemented to obtain the optimal path between a source-terminal pair. Ant Colony Optimization (ACO) and Big Bang-Big Crunch (BB-BC) based routing approaches are applied for different scenarios of WMNs and the performance is compared with the conventional Adhoc On-demand Distance Vector (AODV) algorithm [20].

The remainder of the paper is organized as follows. Section II explains the formulation of hybrid performance evaluation metric based upon Fuzzy Logic. Section III presents the description of proposed soft computing based routing approaches. Node architecture for the proposed system model is presented in section IV. Section V presents the detailed results and discusses the performance and applicability of the proposed algorithms. Conclusions are drawn in section VI.

• II.    Hybrid Performance Metric Formulation

Unpredictable dynamic network conditions critically affect the performance of WMNs and provide corresponding highly non linear statistics for performance evaluation of available links. Fuzzy logic has emerged as a simple yet potent way to solve such non-linear functions of arbitrary complexities with vague, ambiguous or incomplete information while extracting definite conclusions. A basic fuzzy system comprises of four major modules: Fuzzification module, Inference engine, Knowledge Base module and Defuzzification module [21]. The fuzzification module transforms the crisp input(s) into corresponding fuzzy values. These fuzzy values are then processed in fuzzy domain by inference engine based upon the knowledge supplied by the field specialists and produce fuzzy sets as output. Defuzzification module further translates the processed output of inference engine from fuzzy domain to crisp domain. Fig. 1 shows the basic fuzzy system with throughput, end-to-end delay, jitter of the link and the residual energy of the node as inputs and integrated link cost as output.

We prefer fuzzy logic as a suitable faculty to evaluate the integrated link cost of WMNs based upon various input parameters. The proposed Integrated Link Cost (ILC) measure consists of four vital parameters of the link and nodes: throughput, end-to-end delay, jitter of the link and the residual energy of the node. For a link between adjacent nodes high throughput, low end-to-end delay and low jitter are the requisite conditions. A variety of applications in ‘always on’ dynamic multihop WMNs require most advantageous use of node energy. As WMRs deal with more profound traffic load, optimization of energy at WMRs is more significant. Considering the impact of residual energy of a node we have included this parameter to optimize the performance of WMNs. The node having less energy must be used consequently for hoping or other routing purposes. Based upon these four parameters, the hybrid fuzzy logic module evaluates the ILC for the corresponding adjacent nodes and considered as the distance between these particular nodes.

Integrated Link Cost ( ILC ) Г Throughput , Delay , ( Jitter , Residual _ Energy

Integrated Link Cost is a function of throughput, delay, jitter of the link and the residual energy of the node. Initially the current measured values of these inputs are fuzzified and then processed by the inference engine where rule composition takes place. One such rule is given as:

If Throughput is Good and Delay is Small and Jitter is Low and Residual_Energy is High then Link_Cost is Low.

Here Throughput, Delay, Jitter and Residual_Energy are the inputs; Link_Cost is output, Good , Small, Low and High are the linguistic variables. These rules are then implicated by Mamdani implication. The outcome of each implicated rule is a fuzzy set and all these fuzzy sets are then aggregated. The consequential lone aggregated fuzzy set is then defuzzified to present a single crisp output (Integrated Link Cost). Rule base for this system consisted of 81 rules.

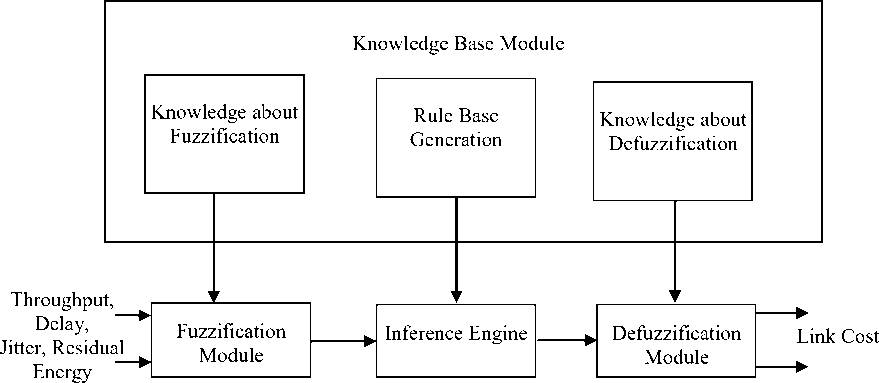
Fig. 1: A basic Fuzzy System with input and output parameters

III. Soft Computing Based Routing Approaches

Routing in WMNs is critically influenced by the highly dynamic network environments. The objective of the routing policies is to maximize probability of data delivery, minimize delay, maximize throughput, minimize energy consumption, dynamically balancing the traffic load etc. This paper explores the application of two nature inspired soft computing based approaches to ensure optimal route selection in appropriate time.

3.1 Ant Colony Optimization (ACO) Based Routing

Ant Colony Optimization (ACO) is a population based probabilistic meta-heuristic approach to solve combinatorial optimization problems by offering ‘good enough’ solutions in suitable time [22, 23]. Social insect societies e.g., ant colonies are distributed systems that cooperatively exhibit intelligent behavior. ACO is inspired by the food searching behavior (foraging) of the real ants. Initially ants search for food arbitrarily. After finding a food source, ants return to their nest while depositing a chemical pheromone trail on the path. Other ants are guided to the food source by the amount of pheromone deposited on various paths.

The Simple ACO (S-ACO) algorithm for selecting the shortest path between source and terminal node in a network is as follows:

An absolutely connected, directed topology graph G (N, L) having N nodes and L links between adjacent nodes with a positive weight (cost) d_i j is given. Neighborhood of an ant k at node i is given as N_i^k while L^k is the length of ant k ’s path. Minimizing the cumulative length of the path (cost) is considered as objective function. Initially a constant amount of pheromone T ij between i t and j t node is assigned to all arcs of the graph. At a node i , the probability of selecting node j as next node with pheromone trails T ij by ant k is computed as

k

pj =

T

a ij

У л^a , ^ l e N ^T il

I0,

if j e Nгf j ^ N

where α is a constant. Previous node is not taken as next node to avoid loops. The ant k at node i further checks its neighborhood and hops from node to node using this stochastic decision criterion until the termination node is achieved. After reaching at terminal node, the forward ant k is converted into a backward ant to retrace the travelled path. The aim of this path retracing is to update the routing information at each node while eliminating the loops. Adaptation to new routing information is regulated by α. While returning to the source node, the ant k updates the pheromone value of arc (i, j) as

k т.. —— т.. + Дт ,

ij         ij              ,

where AT is the increment in pheromone quantity. For shorter paths more pheromone is deposited. The deposited pheromone trails at each arc evaporates similarly to normal evaporation of real pheromone in nature. The objective of the pheromone diffusion process is to avoid quick convergence to a sub optimal route. At arc (i, j) pheromone trails are updated as

T..

ij

— (1 - p)Tj

, P e (0, 1]

where ρ is an evaporation constant. The routing tables obtained are updated at regular interval or at detection of a change in network configuration.

Pseudo Code of the ACO based proposed routing algorithm for WMNs is as given in Fig. 2.

begin/ ACO Parameter Initialization/

Define Source Node, Terminal Node, Number of ants, Number of Paths, Number of

Iterations, Number and location of the nodes

/ End of ACO Parameter Initialization/ while (t < MaxGeneration or Termination Criteria not met)

for i = 1 : n                                                     / all n Nodes / for j = 1 : n                                                / all n Nodes / if distance (i, j) <= R (radio range of a node)

connectivity_matrix(i, j) = 1                  / routing table maintenance /

Integrated_Link_Cost (i, j )= f (Throughput, Delay, Jitter, Residual_Energy) /Integrated Link Cost Evaluation using Fuzzy System/ end if end for j end for i

/ Build paths between source and terminal node /

Randomly generate initial population of k paths

Compute the ILC of all the candidate solutions

Compute the shortest path using S-ACO

Update pheromone trails end while

Postprocess results and visualization;

end

Fig. 2: Pseudo Code of the ACO base routing algorithm applied in WMN

• 3.2 Big Bang Big Crunch (BB-BC) Based Optimization

The Big Bang theory is one of the widely accepted theories of the evolution of this universe [24]. BB-BC based optimization algorithm is another nature inspired population based soft computing meta-heuristic with high convergence speed and low computational time. The BB-BC theory states that energy dissipated by the initial explosion i.e., kinetic energy, is counterbalanced by the energy of bodies attraction known as gravitational pull. If there is sufficient mass so that the later is bigger than the first when a critic density is reached, the expansion will stop and the universe will start to contract, leading to an end very similar to its beginning, named as the Big Crunch (Great Implosion) phase. In the Big Bang phase, energy dissipation produces disorder and randomness as the main feature of this phase. In the Big Crunch phase, randomly distributed particles are drawn into an order. This theory of repeated big bang followed by big crunch phases forms the basis of an optimization algorithm called the Big Bang-Big Crunch optimization algorithm [25].

Shortest path evaluation using BB-BC approach:

Initially a set of candidate solutions (population) is generated randomly in the search space. The fitness as defined by the objective function, of each solution is calculated and ranked accordingly [26]. After the random Big Bang phase contraction is applied in Big

Crunch phase to compute the centre of mass as:

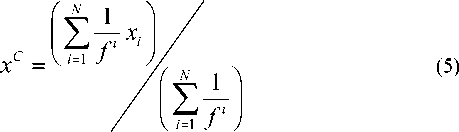
where x^C = position of the centre of mass; x_i = position of i^th candidate; f ⁱ = fitness function value of candidate i ; N = population size.

(Alternatively best fit individual can also be considered as the centre of mass instead of using Equation (5)).

Generate new population around the centre of mass by adding or subtracting a normal random number whose value decreases as the iterations elapse. This can be formalized as new c x = x + ir / k (6)

where l is the upper limit of the parameter, r is a normal random number and k is the iteration step. Then new point x^new is upper and lower bounded. Fig. 3 lists the Pseudo Code of BB-BC based Algorithm for optimal path evaluation in WMNs.

begin/ BB-BC Parameter Initialization/

Define Source Node, Terminal Node, Number of Paths, Number of Iterations, Number and location of the nodes

/ End of BB-BC Parameter Initialization/ while (true)

for i = 1 : n

/ all n Nodes /

/ all n Nodes /

/ routing table maintenance /

for j = 1 : n if distance (i, j) <= R (radio range of a node)

connectivity_matrix(i, j) = 1

Integrated_Link_Cost (i, j )= f (Throughput, Delay, Jitter, Residual_Energy) /Integrated Link Cost Evaluation using Fuzzy System/ end if end for j

end for i

• / Build paths between source and terminal node /

while (t < MaxGeneration or Termination Criteria not met)

Randomly generate initial population of k paths

/ Big Bang Phase /

Compute the ILC of all the candidate solutions

Sort the population from best to worst based on ILC Compute the center of mass xC

/ No.1 path is the Optimal path / / Big Crunch Phase /

Generate new candidate solutions around xC by adding or subtracting a normal

-random Number end while wait for stipulated time/ wait for an event end while

Postprocess results and visualization;

end

Fig. 3: Pseudo Code of BB-BC based Algorithm for optimal path evaluation in WMNs

• IV.    Node Architecture

  Input From Adjacent Nodes

  

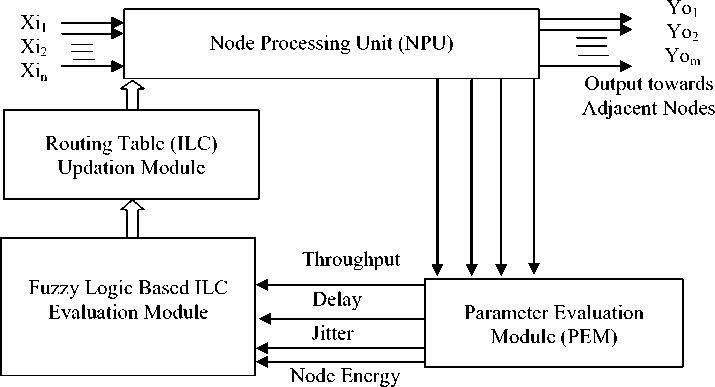
  Fig. 4: Node Architecture of a WMN node

  
  

Fig. 4 shows the proposed node architecture for WMN nodes. At each node there may be multi inputs

(                  arriving from n adjacent nodes) and

• i 1    ^,        i 2 ^,........ i n

• 4. 1 Model Performance

  In order to investigate and optimize the performance of routing algorithm of WMNs simulations were performed for a variety of static and dynamic scenarios in MATLAB. We considered 9, 16, 25, 64 and 100 node networks for infrastructure WMN. These networks were placed within a 500m X 500m, 1000m X 1000m, 2000m X 2000m area. For Client and Hybrid WMNs. 10, 20, 30, 50 and 100 node networks were considered within the same area. We varied transmission range of the nodes from 200 meters to 500 meters. In all the

multi outputs ( Y Y      Y forwarded towards m o1 , o2 ,........ om adjacent nodes). The Node Processing Unit (NPU) makes the decision of identifying the optimal links for corresponding communication within the constraints imposed by the network dynamics. NPU provides this link state information to Parameter Evaluation Module (PEM) to record various link parameters e.g. throughput, delay, jitter and residual energy of the node. Based upon this vital information a Fuzzy Logic based system evaluates the ILCi for the corresponding ith link. The routing tables of all nodes are updated periodically or on the occurrence of some event. The latest information from the routing table is used for routing purposes.

network models node number 1 acts as source and transmits data packets to the last node which is the terminal node (e.g 10th node is the terminal node in a 10 node WMN). The data transmission is made possible through multiple hops via various adjoining nodes. In this type of wireless communication multiple routes/paths are accessible. Decision as regard to which path or route is to be used for any type of traffic, depends upon the current value of the ILC measure (distance).

The proposed algorithms were implemented in MATLAB v 7.6 (R2008a) along with AODV for different architectures of WMNs with varying number of nodes, iterations as well as with different radio ranges and areas. The architectural details are provided in Table 1. The minimal path set is computed by these three approaches for the same network architecture. Table 2 combines the results for Client and Hybrid WMNs and Table 3 shows the numerical results for Infrastructure WMN respectively. Each table represents the integrated link cost and processing time for a specific source-terminal node pair for varying number of nodes and iterations.

Table 1: Architectural details of WMNs

Infrastructure WMN			Client WMN			Hybrid WMN
No. of Nodes	Area (m x m)	Radio Range of a node (meters)	No. of Nodes	Area (m x m)	Radio Range of a node (meters)	No. of Mesh Routers
9	500 x 500	200	10	500 x 500	250	2
16	500 x 500	200	20	500 x 500	250	4
25	500 x 500	200	30	1000 x 1000	350	6
64	1000 x 1000	200	50	1000 x 1000	350	9
100	2000 x 2000	200	100	2000 x 2000	500	20
In the case of Hybrid WMN the number of nodes, coverage area and radio ranges are same as that of Client WMN.

In an infrastructure WMN the nodes are placed uniformly in the specified area constructing a uniform mesh. In this case we assume that there can be at the most 3 adjacent nodes to a given node whereas in the case of Client and Hybrid WMN there can be any number of adjacent nodes to a given node. In order to avoid loops only forward paths are considered in the routing tables. Hybrid WMNs use some fixed WMRs and there are dedicated links among them. Radio range of these WMRs amongst them is double the range of Client nodes.

• V.    Results and Discussion

Client, Hybrid and Infrastructure type WMNs were simulated and the observations were recorded for various network environments. For each of network configurations 20 trials were conducted. The resulting observations are placed on Table 2 for Client as well as Hybrid WMNs while Table 3 presents simulation results for static (Infrastructure) WMNs.

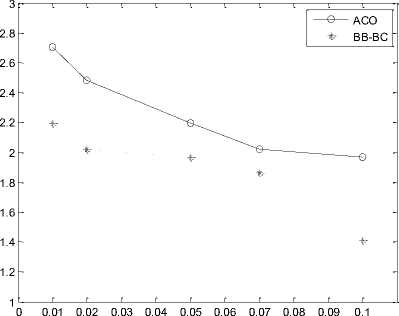
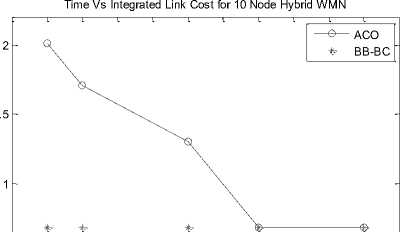
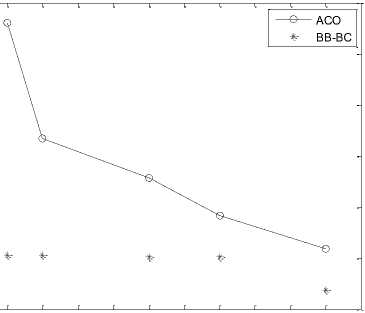
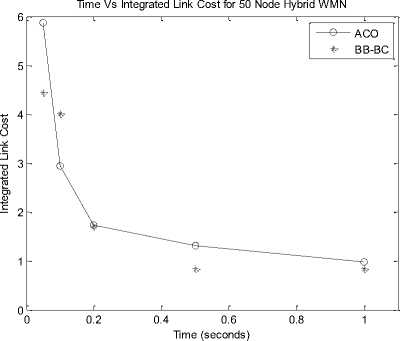
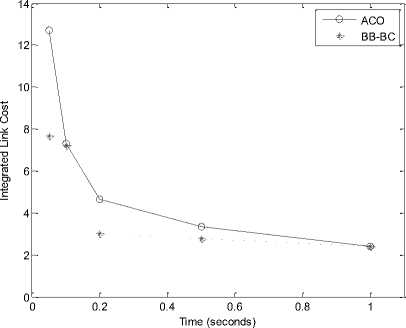
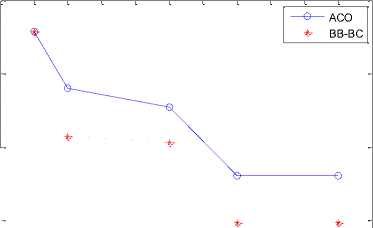
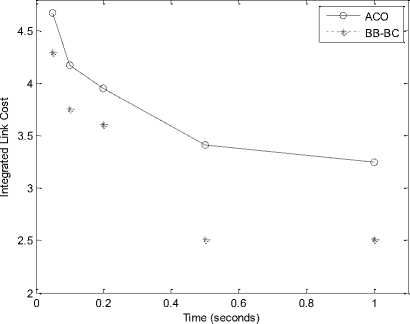
Fig. 5 presents specific network architecture of 10, 30, 50 and 100 node Client WMN. It portrays the random behavior of nodes. Fig. 6 showcases network architecture of 10, 30, 50 and 100 node Hybrid WMN. WMRs are positioned on specific locations and having dedicated links amongst them. Figures 7 and 8 submit Time v/s ILC plot for 10, 30, 50 and 100 nodes for Client and Hybrid WMNs respectively. Fig. 9 draws the Time v/s ILC plot for 9, 25, 64 and 100 node

Infrastructure WMNs. For smaller network architectures the proposed algorithms are simulated for 0.01, 0.02, 0.05, 0.07 and 0.1 seconds while the larger networks are simulated for 0.05, 0.1, 0.2, 0.5 and 1.00 seconds on the same network conditions correspondingly.

It is observed from all these results that proposed soft computing approaches namely ACO and BB-BC outperforms AODV in terms of ILC and processing time. The observations further ascertained that BB-BC performs better than ACO too. In larger networks ACO is unable to converge towards optimal solutions in the given time frame than BB-BC. BB-BC on the other hand converges much easily and with lesser time. As the number of nodes and iterations increase processing time also increases accordingly. It is also observed that these proposed meta-heuristic approaches improve their performance with increasing number of iterations/processing time.

Fig. 5: (a)

Fig. 5: (b)

Dynamic Positioning of 100 Nodes in Client WMN

0    200   400   600   800   1000  1200  1400  1600  1800  2000

X co-ordinates

Fig. 5: (d)

Fig. 5: Network Architecture (a, b, c, d) for 10, 30, 50 and 100 node Client WMN

Fig. 6: (b)

Y co-ordinates

Fig. 6: (d)

Fig. 6: (c)

Fig. 6: Network Architecture (a, b, c, d) for 10, 30, 50 and 100 node Hybrid WMN

Table 2: Results for Client and Hybrid WMNs (20 trials for each set were conducted)

No. of Nodes	Time (seconds)	Integrated Link Cost
		Client WMN			Hybrid WMN
		ACO	BB-BC	AODV/ Computing Time	ACO	BB-BC	AODV/ Computing Time
10	0.01	2.7047	2.1978	2.5474 (0.163764 seconds)	2.0120	0.6828	2.2592 (0.130426 seconds)
	0.02	2.4851	2.0218		1.7058	0.6828
	0.05	2.1978	1.9700		1.3036	0.6828
	0.07	2.0218	1.8616		0.6828	0.6828
	0.10	1.9700	1.4139		0.6828	0.6828
20	0.01	3.0520	1.8942	4.8827 (0.175151 seconds)	3.6441	1.3596	7.3591 (0.139861 seconds)
	0.02	2.9108	1.8942		2.4229	1.3596
	0.05	2.6610	1.8445		1.8044	0.4928
	0.07	1.8942	1.4640		1.1678	0.4928
	0.10	1.8445	1.4640		1.0762	0.4928
30	0.01	10.1011	4.4127	16.0153 (0.203595 seconds)	6.6121	2.0545	14.9558 (0.160448 seconds)
	0.02	4.5485	3.8623		4.3458	2.0545
	0.05	4.4127	3.7073		3.5761	2.0210
	0.07	3.8796	2.5192		2.8328	2.0210
	0.10	3.8623	2.5192		2.1761	1.3794
50	0.05	6.4157	5.1492	11.3544 (0.376226 seconds)	5.8640	4.4491	12.4939 (0.312940 seconds)
	0.1	3.5586	3.0320		2.9354	4.0093
	0.2	2.2618	1.8399		1.7261	1.7192
	0.5	2.2357	1.3540		1.3016	0.8356
	1.00	2.1373	1.2400		0.9700	0.8356
100	0.05	13.0705	6.6234	17.4170 (0.486520 seconds)	12.6959	7.2289	14.0850 (0.347388 seconds)
	0.1	7.8583	3.0858		7.3142	7.6650
	0.2	5.8813	2.4780		4.6477	3.0016
	0.5	4.4013	2.3804		3.3216	2.7494
	1.00	2.5261	2.1328		2.4112	2.4112

Integrated Link Cost                                                                                                                                                                      _{Integrated Link Cost}

—X                                                                            Integrated Link Cost

Time Vs Integrated Link Cost for 10 Node Client WMN

Time (seconds)

Fig. 7: (a)

Time Vs Integrated Link Cost for 50 Node Client WMN

ACO t- BB-BC

0.4          0.6

0.8             1

Time (seconds)

(c)

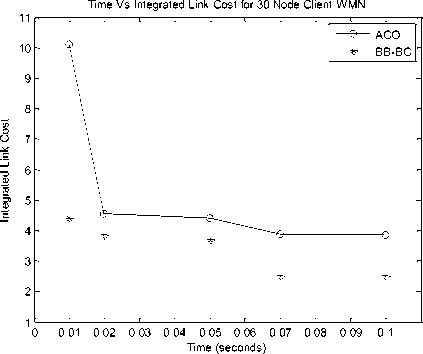
Fig. 7: (b)

Time Vs Integrated Link Cost for 100 Node Client WMN

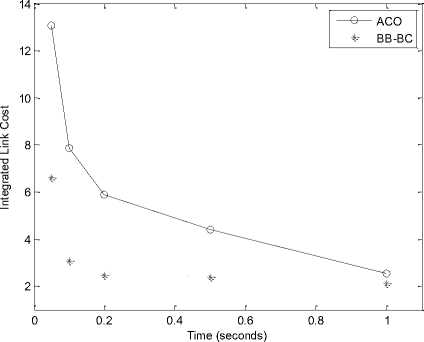
Fig. 7: Time v/s ILC plot (a, b, c, d) for 10, 30, 50 and 100 node Client WMN

0.5

0 t--------Г--------Г--------Г--------Г--------Г--------£--------Г--------Г--------Г--------L_

0   0.01  0.02  0.03  0.04  0.05  0.06  0.07  0.08  0.09  0.1

Time (seconds)

Fig. 8: (a)

(d)

Time Vs Integrated Link Cost for 30 Node Hybrid WMN

0   0.01  0.02  0.03  0.04  0.05  0.06  0.07  0.08  0.09  0.1

Time (seconds)

Fig. 8: (b)

(c)

Fig. 8: Time v/s ILC plot (a, b, c, d) for 10, 30, 50 and 100 node Hybrid WMN

Time Vs Integrated Link Cost for 100 Node Hybrid WMN

(d)

Table 3: Results of Static (Infrastructure) WMN (20 trials for each set is conducted)

No. of Nodes	Time (seconds)	Integrated Link Cost
		ACO	BB-BC	AODV/ Computing Time
9	0.01	1.8229	1.5975	1.9718 (0.175786 seconds)
	0.02	1.3636	0.6939
	0.05	1.1489	0.4231
	0.07	0.6756	0.3280
	0.10	0.3280	0.3280
16	0.01	3.5454	2.0301	4.4739 (0.186687 seconds)
	0.02	2.9189	1.8233
	0.05	2.5893	1.6868
	0.07	2.1302	1.0366
	0.10	1.0366	1.0366
25	0.01	2.2851	2.2851	3.5240 (0.221019 seconds)
	0.02	1.9007	1.5743
	0.05	1.7727	1.5317
	0.07	1.3059	0.9834
	0.10	1.3059	0.9834
64	0.05	4.1993	5.2291	3.5240 (0.299706 seconds)
	0.1	4.0391	3.1497
	0.2	2.6559	2.5492
	0.5	2.5492	2.2132
	1.00	2.5492	2.0972
100	0.05	4.6709	4.2958	12.0776 (0.360641 seconds)
	0.1	4.1707	3.7580
	0.2	3.9522	3.6113
	0.5	3.4125	2.5151
	1.00	3.2457	2.5151

2.5

ACO

*- BB-BC

Time Vs Integrated Link Cost for 9 Node Static WMN

1.8

1.6

1.4

1.2

0.8

0.6

0.4

0.2

0.01  0.02  0.03  0.04  0.05  0.06  0.07  0.08  0.09  0.1

Time (seconds)

(a)

Time Vs Integrated Link Cost for 64 Node Static WMN

ACO

--*--- BB-BC

Time Vs Integrated Link Cost for 25 Node Static WMN

1.5

0.5 t----------1----------1----------1----------1----------1----------1----------1----------(----------1----------L_

0   0.01  0.02  0.03  0.04  0.05  0.06  0.07  0.08  0.09  0.1

Time (seconds)

(b)

0.2          0.4          0.6          0.8

Time (seconds)

Time Vs Integrated Link Cost for 100 Node Static WMN

(d)

(c)

Fig. 9: Time v/s ILC plot (a, b, c, d) for 9, 25, 64 and 100 node Static WMN

• VI.    Conclusion

This paper proposed two new nature inspired optimal path evaluation algorithms to implement shortest path routing in WMNs. This paper presented a new fuzzy logic based hybrid integrated link cost metric that took into account throughput, delay, jitter of the link and residual energy of the node as performance parameters. Based upon these parameters the enumerated ILC was considered as the distance between two adjacent nodes. This ILC was further used to enumerate path costs between specific source-terminal node pairs. Based upon this effective ILC based performance metric three routing algorithms i.e. ACO, BB-BC and AODV have been applied to establish the optimized path between a specific source-terminal node pairs. The proposed ILC measure is scalable and quickly adapts to the stochastic behavior of WMNs. All these routing approaches are applied to 10, 20, 30, 50 and 100 node client and hybrid WMNs while 9, 16, 25, 64 and 100 node network architecture is considered for infrastructure (static) WMNs with various network topologies. The proposed soft computing based routing approaches were simulated for 0.01, 0.02, 0.05, 0.07, 0.1, 0.2, 0.5 and 1.00 seconds for the same network topology. Effect of Time over ILC is recorded for the proposed soft computing based meta-heuristic routing policies.

The extensive simulations conducted, show that BB-BC based routing strategy quickly adapts to the dynamic network conditions of WMNs followed by ACO and lastly AODV. It is observed from the results obtained that BB-BC based routing approach yields best results in terms of ILC however ACO and AODV are selecting non-optimal solutions. The ACO based routing algorithm is slower in converging to the optimal solution. Its performance was observed to be better than AODV. For smaller networks, BB-BC based approach converges to the optimal solution in very less time while ACO was found to improve its performance with time. For large WMNs BB-BC based routing approach outperforms other routing strategies in terms of ILC.