Identification of Parametrical Restrictions in Staic Systems in Conditions of Uncertainty

Published Online March 2013 in MECS

Parametrical restrictions are a basis of creation of effective systems of identification and control. In systems of identification the account of restrictions allows to reflect real working conditions of object and to realize robust algorithms of a parametrical estimation.

In identification systems the set of publications is devoted application of parametrical restrictions. In [1] the problem of identification of model of the price of the basic assets by means of extension of the general method of moments is considered. Two types of the restrictions superimposed for a moment are considered. These are restrictions on current value of a variable or on as maximum value for a variable on some interval. Restriction on the moment is set a priori. In [2-4] application of the general method of the moments for a correlation establishment between parametrical restrictions and stability of parameters is given also. Restriction is set in the form of equality for the moment. As well as in [1] restrictions are set a priori. In [5] the problem of identification of parameters of process of electromagnetism in the availability of existing physical restrictions on parameters is explored. Iteration algorithm Levenburg-Marquardt is applied to its solution. APR it is set a priori in the form of the lower and upper boundaries on a modification of parameters. The problem of correction of set boundaries of restrictions is considered. In [6, 7] the problem of parametrical identification of dynamic object subject to the parametrical restrictions representing a parametrical ellipse is studied. Quadrati-cally constrained limited method of least squares is applied to a problem solution. The heuristic algorithm of a solution of a problem is offered. In case of the final data in [6] is shown, that always there is some indefinite square restriction, depending on operating noise. The solution of a problem of optimization taking into account existing restriction is reduced. It is shown that the solution contains true parameters of system at performance of a condition of a constancy of excitation of an input. Restrictions are set a priori. In [8] the problem of an estimation of parameters of nonlinear polynomial model on the basis of the account of a priori knowledge is considered. The ellipsoidal algorithm is applied to its solution. Restrictions on parameters are set on the basis of the analysis polynomial the equations for an evaluation of parameters. The algorithm of identification has a heuristic form. In [9] the problem of identification of static object with a priori set area of parametrical restrictions is considered. For probability of an exit of estimations of parameters estimations are received for boundaries of area of restrictions. A priori set APR in a problem of construction of model of an autoregression of process of electric stimulation of muscles work [10] is devoted the influence. It is noticed that ignoring of parametrical restrictions affects results of a parametrical estimation. The case of correction of restrictions is considered. It is shown that the account of restrictions improves predicting properties of the identified model. In [11] the method of synthesis of algorithm of identification of dynamic object with a priori set restrictions on parameters in the form of equality is offered. The variation method of determination of an optimum of function of Hamilton is applied to synthesis of algorithm of identification. Paper [12] proposes a closed-loop system identification procedure that aims to improve model parameter estimates by incorporating prior knowledge about the process in the form of constraints without the use of a dither signal. It is shown how to generate restrictions on the basis of the a priori data about object. Newton's method is applied to optimization of criterion of an estimation with restrictions.

In work [13] the problem of use of a priori knowledge of plant and to their representation in the form of restrictions in system of identification of nonlinear system is considered. For a problem solution the generalized method of least squares is applied to an estimation of parameters. In [14] the problem of an estimation of parameters of plant with application of a method of least squares and square restrictions is studied. For construction of restrictions physical knowledge and a regularization method are used. Algorithms of identification are offered and are shown their application. In [15] the problem of an estimation of parametrical restrictions in a problem of damping of oscillations in nonlinear control systems of mechanisms with elasticity is considered. The analytical mode of a choice of roots of a characteristic polynomial of the closed system of the fourth and fifth orders is applied to definition of restrictions. The system model is set a priori.

Some approaches to a solution of a problem of deriving of parametrical restrictions are offered in [16, 17]. In work the mode of deriving of parametrical restrictions for dynamic linear system on the basis of the analysis of an observable informational portrait is described. Specifically, for estimation APR Ω ^A set in the form of an inequality on norm of a vector of parameters, the majority model was applied.

From the analysis of works follows that parametrical restrictions are often used at synthesis of systems of identification. Usually the area of parametrical restrictions is formed a priori. Algorithms of correction of area of restrictions Ω ^A have heuristic character. The problem of construction Ω ^A in the conditions of a priori uncertainty was not considered. But there is a whole class of complicated objects for which to set description Ω ^A a priori not probably. Therefore the solution of the given problem for the specified class of systems is actual.

The approach to construction of area ΩA for static systems in the conditions of uncertainty is offered in [17, 18]. The method of an estimation of area ΩA specify in the form of the lower and upper boundaries of a modification of parameters of system is offered. The method is based on a domination principle. The iteration algorithm of correction of the received estimations of area of restrictions is offered. The criterion of an assessment of works of system identification is introduced. Properties of an iteration scheme are researched. The adaptive algorithm of an estimation of parameters of area ΩA on the basis of processing of the current information on system is offered. Convergence of adaptive algorithm is proved. Then the case of the representation of area ΩA in the form of restriction on norm of a modification of parameters is considered. The solution of a problem for a case, when the norm looks like restriction on a modification of a maximal element of a vector of parameters of system is received. To a problem solution it is applied two approaches. The first approach is based on correction of received estimations ΩA and application of a principle domination. The second approach is based on adaptation of parameters of the model, depending on performances of area restrictions. Boundedness of received estimations of parameters of model is proved. To a solution of the considered problem it is applied a method of secants. Generalisation of the received results on other forms of vectorial norms is given. Results of modelling confirm working capacity of the offered methods and algorithms.

• II.    Estimation of Area Ω ^A in the Form of an Interval of a Modification of Parameters

Consider system y _n = A _n ^TU _n + ξ _n ^,

where ^{An ∈ Ω A ⊂ R} there is a vector of parameters, belonging of the limited area

ω _A = { A _n ∈ R^k : φ _{b , i} ≤ a _{i , n} ≤ φ _{t , i} , ( φ _{b , i} , φ _{t , i} ) < ∞ , }    ₍₂₎

with unknown φ _{t , i} ∈ Φ _t ∈ R^k , a i , n ∈ A n , N < ∞ ,

parameters n ∈ J N = [0, N ]  _is

φ _{b , i} ∈ Φ _b ∈ R^k

,

discrete time,

U n ⊂ R

k is a vector of an input with ui,n ∈Un, ξn∈R is the lim- limited irregular variables

ited perturbation operating on an output of object.

For object (1) information I ^o = I ^o ( y ⁿ , U ⁿ ) is known and observable informational portrait Γ ^о : { U ⁿ } × { y ⁿ } is constructed. Introduce vector ^ ^co^^{( Ф t} 1^{, ф ,2 ,}^^{, ф t} , k ) which majority vector A ⁿ in (1). Consider the special case of area Ω ^A corresponding to an upper bound of area of restrictions

Ω _{A , t} = { A _n ∈ R^k : a _{i , n} ≤ φ _{t , i} , φ _{t , i} <∞ , a _{i , n} ∈ A _n }

.

To estimation t ∈  A,t apply mathematical model yˆt,n = Φˆ Tt Un

.

Problem: for plant (1) on the basis of analysis I ^o and

Γ map о receive by means of model (3) such estimations of vector Φt in (2) to satisfy a domination condition

Calculate average values

ˆ t,n    n for almost ∀n ≥ 0 .

We understand performance of inequality

(4) y _n ≤ y ˆ _{t , n}

NN 11 y =   ∑ yn  yt,0 =   ∑ yt,0,n n=0                n=0

and define variable

as domination for almost ∀ n ∈ J ^N

.

^ε t ,0 ^{= y - y ˆ} t ,0    ^{∃ Φ} t ,0

.

Lemma [18] . ε ^{t ,0} ≠ 0

.

It is possible to apply some approaches to a problem solution. State one of them [19], based on check of a condition of domination, using as secondary criterion average value of study variables.

Consider projections of observable informational port r ait Γ ^o to planes ( u ⁱ , y ) and construct secants γ ^{y ( u i ) ∈ R} by means of a method of least squares

ε                             yˆ t,0 shows how much variable  t,0,n does nearer to domination area over yn . If εt,0 ≤

not

A

come

y t ,0 ^ У ,                         ,

then almost ∀ n ∈ J ^N . On the basis of ε ^{t ,0} generate set _ˆ

Φ of corrections of a vector for  t,0 . For this purpose de fine magnitudes

γ _y ( u _i ) = a _i u _i + b _i   i = 1, k

,

with ranges of definition and values:

dom( γ _y ( u _i )) ∈ J _{u i} ^,

~ ε     ε t ,0

φt,i,n = ui,n  ∀n ∈ JN

rng(γ (u)) ∈ J J ∈ R J ∈ R y i y , where ui , y are intervals of a modification of variables ui, y ; ai,bi are some numbers.

ε    ε ~ε and calculate their average values t,i    t,i t,i,n . Gen erate a vector of corrections

Афt,0 = ф Ф^ -Ф"k 11

.

ˆ

Let t,i,0   i . Then we have the approached estima tion of area ΩA,t

ˆ

Correction of vector  t,0 fulfill by means of algo rithm

^Φ t ,1 ^{= Φ} t ,0 ^{+ Γ} t ^ΔΦ t ,0

,

Ω ⁰ A , t = { A n ∈ R ^k : A n ≤Φ ^ˆ t ,0 }

ˆ    ˆˆ   ˆT with Фt,0 = [фt 1,0 фt2,0 —фt,k,0]

.

ˆ t,0 we understand inequality as single-item. The index 0 designates level of a small adjustment of ˆ vector t of model (3) and does not coincide with a step of a modification of interval JN .

ˆ

Φ

Apply model (3) with   t,0 and define prediction yˆ t,0,n of an output of object n and magnitude of coef-r2

ficient of determination yt,0y . Check up a condition of v.„  > y domination  t,0,n    n . If it is fulfilled for almost all n suppose   A,t =  A,t,0 and process of definition APR finish. Otherwise apply algorithm of correction   A,t,0

for the purpose of performance of a condition (4).

Γ ∈ Rk×k                        γ >0

where t        is a diagonal matrix with t,ii . Ap- yˆ ply model (3) and define prediction 1,n for n

ˆ ^r ˆ

^N . Define    ^{t ,1} and ^{y t ,1 y} . If   ^{t ,1}       and

r - ryyˆt,1

—

^{r yy ˆ} t ,0 ^{≤ Δ r} 0 < Δ _r < ∞

,                                   ,

Ω = Ω (Φ )

Then suppose   A,t    A,t  t,1 and on it process of construction APR finish. Otherwise apply algorithm (9) ˆ to adaptation of vector t . Here r there is some set magnitude.

ˆ

Statement 1. Let initial value of vector ^t is defined on the basis of secants (5), and its correction in the equation (3) is realize according to (8), (9). Then estimation APR

^ω A , t ⁼ { ^A n ^{∈ R k | a} i , n ^{≤ φ} t , i ^{, φ} t , i ^{<∞ , a} i , n ^{∈ A} n }    ₍₁₀₎

is admissible, if the condition of domination y 1 1, n ^ y n for almost V n e J is sa^^ and

Г'

^{ry ˆ} t ,1 ^y

∈Ω ={r ∈R:r r        yt,1y            yt,1y

-

f- < A . 0 < A <  r _{y ˆ t ,0 y} ≤   _r ,   ≤ _r < ∞

The condition (11) superimposes restriction on a class of acceptable models (3) in the conditions of un-

Ω                ryˆ y certainty. For the centre of area r accept value  t,0 .

where Nm ⊆ Z ⊂ R there is a set of integers for which ˆ it is fulfilled (13), * m is an iteration step on t,m for which it is fair (14). Fulfillment (14) corresponds to such values of an exit of model (3) for which receive maximum value of an informational potency [17]

Remark 1. In (7) instead of ε ^{t ,0} is possible to use flowing (on time n ∈ J ^N ) value of misalignment ^ε t ,0, n ^{= y} n ^{- y ˆ} t ,0, n

N

1       _ˆ 2

y=N∑yi i=1      .■

.

Remark 2. If processes in system have stochastic character for decision-making on domination it is necessary to set admissible level of domination (see indica-р ■ tor -y ).

The algorithm (12) is finite-converging algorithm. Its properties receive from the following theorem.

Theorem 1. The system of identification (1), (3) and

(12) with ^{Φ ˆ} t , m ^{∈ Ω} A , t

an acceptable vector of parameters

ˆ

Generally algorithm of adaptation of vector   t,m present as

Γ ∈ R

k×k in

has the limited trajectories, if for matrix

algorithm (12) the inequality is fulfilled

2          2            .

^Φ t , m + 1 ^{= Φ} t , m ^{+ Γ} t ^ΔΦ t , m

,

^λ t ²,max ^{( Γ} t ^{)    2( δ A} t , m , n ^{) T ΔΦ} t , m

λ t ,min ( Γ t )        || ΔΦ t , m || ²

,

where    t,m =    t,m(n) is formed on the basis of ap plication to the procedure stated above.

For an estimation of quality of work of system of identification of parameters of area Ω ^A introduce quan-

У - y titative criterion. Consider that t,n n almost on all interval JN , if probability

where

λ  ( Γ )   λ  ( Γ )

^{t ,min t} ,   ^{t ,max t} are minimum and maxi-

ˆ mum eigenvalues of matrix t , t,m n    t,m . Op-

Γ timal value of matrix  t

p - y _t = ^P ( y t , n ^ y n ) ^ p >■   v n e J N

,

Γt = D(δAt,m,n)D-1(ΔΦt,m) , where D is an operator of transformation of vector t,m,n in a diagonal matrix.

where p ^- >  ⁰ there is a given magnitude.

Φ ^ˆ   ∈ R ^k

Definition 1. Vector  t,m     name optimum if he allows to receive an acceptable estimation of area of parametrical estimation   A,t and ensures maximum value of indicator  -yt .

Similarly define the lower boundary for area Ω ^A (2). In this case a condition of domination (4) write in the form of y b , ⁿ ^ y ⁿ for almost ^{v n} ^ 0, where y ^b , ^{n e} R is a model exit

ˆ         ˆT yb, m, n      b,m n

Statement 2. The exit of model (3) with vector Φˆ  ∈ Rk t,m      corresponding to an optimum majority esti-

ˆ mation of area  A,t  t,m , has a maximum information al potency.

Proof. Consider acceptable exits of model (3) for which conditions of the statement 1 are satisfied, and the domination indicator satisfies (13 Hence, as an optimum majority estimation of area ^{A , t} consider that, for which

Φ ∈R with a vector of parameters   b,m

Φˆ tuning   b,m

2       2

=Ф, b , m +1       b , m

-

^Γ b ^{ΔΦ ˆ} b , m

.

k

. Algorithm of

ΔΦ ∈ R ^k

Misalignment     ^{b , m}      receive from (7) and (8)

Γ ∈ Rk×k taking into account remarks 1, 2. In (15) b        is a

γ > 0

diagonal matrix with   ^{b , ii}    . Properties of algorithm

(16) receive from analogue of the theorem 1.

max P ( y ˆ    ≥ y ) = P  ( k )

k e N m    k ^, k ^, n   n^{n     -} y t      v n e J N

,

2.4. Adaptive algorithm of definition of parameters of area ^ A,t

To tuning of vector  t,n in (3) apply adaptive algo rithm

^Ф t , n - Y ⁽y n - У п U n , ( y n ^ У п ) V ( r yy ⁶ ^ r ),

Ф t , n ,         ^{( У} n ^ У п ) ^{Л (} r yy ^e ^ r ), ^^

where ^Y >  0 there is a parameter ensuring convergence of algorithm.

Now specify criterion of a belonging of an exit of model (3) of area

where e ^{n   У п   У п} .

The algorithm (22) converges at

⁰ <  ^Y <  У ¹ ,

Ф t , n + 1 = ^

У = max \\ U n \\ ² where       ⁿ

Optimal value ^Y define from condition

5AV, /5y = 0  Yont = У-       у у    Ym ф,n         : oppt       . At such choice opt for a case of performance of a condition of domination (4) (\ e„\> c)

ⁿ      receive

Ф = { У п e R , У n e R : У n ^ У п almost for V n e J n }

^A V o , n <

—

e ² <

У ²

c ²

—

У ²

c >  0

.

To decision-making on quality of work of algorithm P ˆ

(17) apply indicator    ^{У t} (13) on interval N .

The algorithm (17) belongs to the class finite-converging, and (13) is a condition of decision-making es timate to A,t .

As the solution on final interval J ^N for number of errors ^m of algorithm (17) receive is defined

д Ф 2п m <  -Ut° У ²

c ²

. ■

Theorem 2. Let vector U ^{n e} R in (1) satisfies to a condition of a limiting nondegeneracy, and ^{t ,0} in (17) is on the basis of construction of a field of structures on set of secants. Then the algorithm (17) allows to receive the admissible estimation of vector ^{t , n    A , t} ensuring

У . >  У.

performance of target inequality ^{n n} , if

0 <  Y <----у | U n || ²

Some modifications of algorithm (17) are possible also. In particular, it is possible to demand performance of a condition ^S -domination [17]

^У >" У ^ ^{( У —} У ) >  S s

^ У                ^У    § У >  0

It is necessary to notice that the condition (18) toughens requirements to algorithm (17). A payment for it is magnification of value ^{A r} in (11). There is limit ^{У у} above which the ^S -domination condition is not realized.

,

and the relative number of errors of algorithm on interval J ^N is equal

m <

| ® t ,0 I²

д

У

У ² = max || U n \\ ² where       ⁿ

^ Ф t ,0 =^Ф t ,0 ^-Ф t

Proof. Write algorithm (17) are comparative misalignment

дФ t , п = д Ф t , п - 1 - Y ( У п - У п U n ,

к     ^ Ф? п = Ф? и - Ф?

where      t , n      t , n     t .

Consider Lyapunov function V®,п  11 ^t,п 11 . For the first difference A^®,n     n  Фф’n-1 receive

A V o , n —еп д фф- ! п - U n + Y ² e 2\\ U n II ²

2.5. Example

Consider object (1) with a vector of parameters A = [0.3 — 0.81]r .                  i       + д and additive irregular limited perturbation ^n e R operating on an output, \ ^n \ < 0-3. Elements of vector U e R are the random functions having final expectation and a variance. It is necessary to estimate area of parametrical restrictions (2).

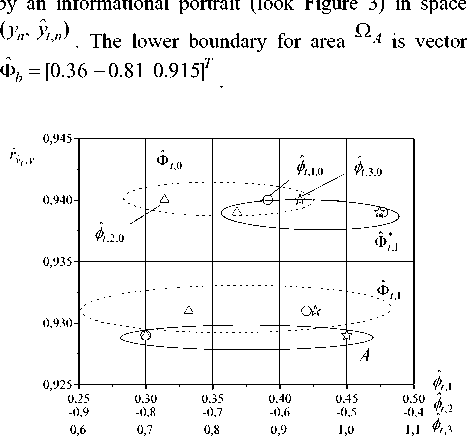
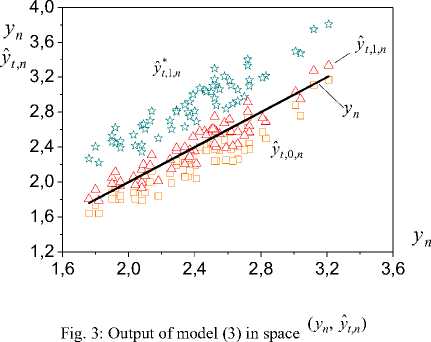
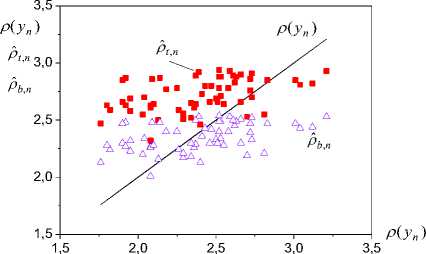
On Figure 1 results of identification of vector ^Ф t for area ^{A , t} by means of system (3), (7) and (12) are shown. Here the vector of parameters A ⁿ of object (2) is shown also. The method of least squares gives the following     estimation     of     vector      ^A :

A = [0.38 — 0.7 0.96]T      t    фн    . ф*1 . r n                         . Vectors t,1 and    t,1 define by means of algorithm (12) with Г/ = 0.3I3 and Г/ = I3,

I ∈ R3×3                                  r where 3        is an identity matrix. Values yty are

*

r = 0.94 r = 0.935 r ^*   = 0.939

equal ^{y ˆ t ,0 y}           ,   ^{y ˆ t ,1 y}             ,   ^{y ˆ t ,1 y}

.

According to the statement 1 received estimations are admissible. For final For each of the received estima

P. y о = 8% tions they are equal (Figure 2):     yt,0         ,

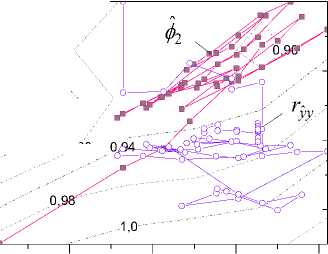
P.y, = 55% P- = 100% t,1        , t,1          . The same results are given that the received value of vector Φt is admissible, as ryyˆ r . Tuning of parameters of model (3) by means of algorithm (15) show on Figure 5. In figure level lines rˆ for yy are shown, the line with a circle reflects modifi- rˆ cation yy , and with quadrate is a modification of pa- rameter φ2 .

Φ

Fig. 1: A vector estimation

1,2

p °- p¹

¹ . y , ¹ . V,

1,5

0,8

0,4

0,0

1,0

0,5

0,0

P °-. yt

1,6    1,8    2,0   2,2    2,4   2,6    2,8    3,0    3,2    3,4

p 1*

ˆ

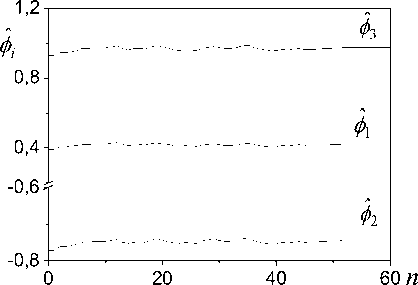
Fig. 4: Results of work of adaptive algorithm (17)

-0,5

y _n

ˆ

Fig. 2: Domination of variable

at various values of vector

Φ ^ˆ t

On Figure 4 results of work of algorithm (17) are

shown at an estimation of area   ^{A , t} of object (1) with a

A =[0.3 -0.8 1]T vector of parameters                   . Initial estima-

ˆ tion     t,0   of vector     t in (3) is vector

[0.39 -0.770.93]T received on the basis of the analy-

As it has been told in section 2.4, there is limit ^y above which the δ -domination condition is not realized. For algorithm (17) after definition of estimations APR taking into account a condition δ -domination (18) in-

^P . y = 0.8

dicator ^δ       , and for the same algorithm for a

y . y           P t = ^0.6

condition of domination nⁿ nⁿ indicator y

.

sis of a field of secants. For considered case

P . y = 0.77

^{y = .} . Adequacy of the received models by criterion

P                                    P . - = 0.65

. with usual and     -domination:     y        ,

P . y = 0.8

.

and p. it is equal 0,6. Values of cross-correlation co- efficients

r yy ˆ ₀ = 0.94

and

r yy ˆ = 0.939

have confirmed

-0,74

ˆ ф2

-0,75

-0,76

-0,77

0,86

0,90

ˆ ф2

Г-ry ˆ y

1,0

1,00

^ry ˆ

0,96

0,92

0,88

0,40     0,41      0,42     0,43 ф

"

ˆ ^ˆ

If ^{y t      y} , then estimation ^{t ,0} improve. Consider

/X m v„ — ATU model n L n and apply a method of least squares

ˆ to definition of vector L . On the basis of model v„ — ATU n       n define the prediction of output n of object.

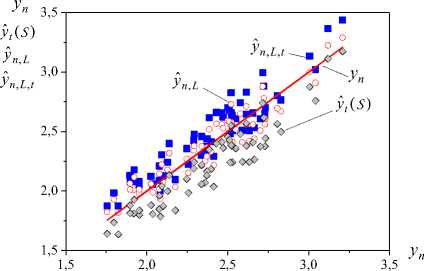
Generate informational set

I LSM ^{— { y} n , L ^G R , U n ^G R k , ^{n G} J N ^{}    y} n , L ^{— y} n

Construct a new field of structures

Fig. 5: Results of work of algorithm (17) in space

( ^ф > ^ф 2 r yy )

S S ^{( y} L ) ^{— {} Y ^{( y} L , u i ) ^V i ^— 1, k ^} ,  ^{( y} L , u i ) ^G I LSM ,

So, results of modelling confirm efficiency of the offered approach.

• III.    Estimation of area ^ A on the basis of the analysis of a field of secants of system

• 3.1.    Approach description

Reduce a solution of a problem from section 2, using results of the analysis of a field of secants of object (1). Apply to identification of area of restrictions (2) objects (1) set of experimental data where Y(Уl,ui) — Yi,l — a0,i + ClVUi,n .

For each secant Y1,L calculate value yY1,L . If the condition is satisfied ryYi, l - ryYi   V i — 1, k

ˆ then specify vector t,1 on the basis of coefficients ci                      Y-1

• ^{1, i}    of secants   ^{i , L} . Otherwise to corresponding ele-

• ˆ

ment of vector   ^{t ,1} appropriate value from

ˆ

^Ф t ,0

I o — {Уп G R, Un G Rk, n G JN } ф — со1(ф ьфг,...,ф. Л

For an estimation of vector t        t,1 t,2     t,k setting an upper bound of area ^A (2), apply following the approach. Construct for (1) field of secants [18]

ˆ

Apply model  n,L*    t,1 n to the prediction of output yn of object. The prediction of values yn received by

ˆ         ˆT means of model n,L*    t,1 n , designate through yn,L,t

.

Calculate Уn,l,t   Уn,l,t(Уn,l,t(S(Уn,l*)) and ryy”■ l■ t(S)

conditions are satisfied

S s ⁽ y ) ^{— {}Y⁽. y , ^u i ) V i ^— 1, k ^}

,

.      Y(У, ui) — a 0,i + a 1,Ui ■             + a0,i, a 1,i where               ,      , is a secant, ,     , are some real numbers. Y(y’ ui) approximates a contraction

Г of observable informational portrait o of object (1).

^{( y} n , L , t >  У )& ⁽|

^{r yyˆ} n , L , t ^{( S )}

- r yy t ( S )| ^ ^§ r )

ˆ where r , then we accept t,1 for the upper esti-

ˆˆ mation of area A :   t    t,1 . Otherwise fulfill correc-

For ^{y ( y} ’ u i ) define cross-correlation coefficient ^{y Y i} .

To field SS(y) corresponds the observable informational portrait set by map Г° : {Un} x {yn} . Accept pa-ˆ rameters  1,i for initial estimations t,0 of elements of

^

л

ф                ф vector   t in (3). On the basis of   t,0 , using model (3), make the prognosis of an output of object (1). Designate the received variable through yt(S) . Calculate ryyˆt(S) and averages for yt(S) and y .

ˆ tion of vector t , using for this purpose the adaptive procedure described in the previous section. As informational set use ILSM .

This approach apply to definition of the lower boundary of area ^ A (2). Use a condition of domination ^y t ⁽ S ) ^ ^y - If it is not fulfilled, apply model

• — ф T ,u

Уb , n     b , n ¹ n and analogue of algorithm (17).

A — [0.3 — 0.8 1]^r_л

Consider plant (1) with vector                  . As

ˆ initial estimation      t in (3) use vector

IV. Estimation of area ^ A in the form of restriction on norm of a modification of parameters

Consider system

analysis of a f ield of

У — 2.39. As У t ( S ) <  y

secants S ^{5 ( У} ) . ^У t ⁽ S )   ^2.2 ,

the condition of domination

Ф with estimation t,0 is not fulfilled. On the basis of the analysis of a field of secants S(yn,L) receive estimation

A           ф.

^{t ,1}   of vector ^t :

rP, L ~ rPi   ^ф t ^— A t ,1

,

A.                                                            rp

A t 1 — [0.396 — 0.76 1.012] T .

^,                                . As

y ˆ

. For variable   ^{n , L} the condition

У п — A T U n + ^ n

,

where vector A n ^e R belongs a priori to unknown area

^ A ^— ( A n ^e R k ^{: a} b < 1 A n II <  ^a t , ⁰ <  ^{( a} b ^{, a} t ) < 4 , (19)

of domination r       — 0.94

yy n , L , t ( S )

, Pˆ domination    yL,t

A . —

У n , L , t >  У

_J r — 0.94 , and      ^{yy t ( S )}              ,

y n , L , t   ^2.48 is satisfied. Indicator of

— 0.7

U e R                 y e R n       is an input vector, n      is an output,

^ ^{n e} R is the limited perturbation operating on an output of object.

For object (18) the informational set is received

received estimation shown on Figure 6.

. Results of adequacy of the of area of restrictions ^{A , t} are On Figure 6 following labels are

used: y is a straight line, yn,L is a circle, yt(S) is a yˆ rhomb,  n,L,t is a quadrate.

As y t ⁽ S ) ^ ^У for the lower boundary of area of restrictions ^A accept vector ^{b 0} . For model with Ф                          P. — 0.98

^b an indicator of domination ^yb       .

Fig. 6: Results of an estimation of area (2) on a domination plane

I o ^— I o ⁽ У п , U n , n ^e J N ) .

It is necessary on the basis of the analysis of set I ^o on the set class of structures of object (18) to estimate parameters ^a b ^{, a} t of area (19).

The considered problem substantially differs from the statement stated in the previous sections. The representation of area ^ A in the form of (19) does not allow to apply the approaches offered earlier. It explains nonlinearity of a considered problem as on parameters, and informational variables. The main thing here is a choice of suitable vectorial norm which in many respects depends on properties of vector U ⁿ and its correlation with output y ⁿ . Depending on applied norm receive various estimations for area ^ A . As shown in [16], for norm of vector A ⁿ in (18) receive the following estimation

a t _b <  || A n || i t

^, where

аь ^—

max | yn | n e JN______ max || Un || n e JN

max | yn | n e Jm a — —N--- min || Un || n e JN

.

So, the method of an estimation of area of parametrical restrictions (2) for object (1) on the basis of the analysis of a field of secants is offered. In certain cases it is necessary to apply a two-level field of structures to consider features of existing informational set of the data of object (2). It is true for the objects which inputs belong to a class of irregular functions.

In [16] it is shown that the upper bound for norm of vector A ⁿ is overestimated. Explain it both the applied approach, and an operation on an exit of perturbation L Ct.

ⁿ . Therefore estimation ^t specify in the process of identification. If y ⁿ and U ⁿ are measured with errors in (20) use their smoothed values.

Apply as norm function [20]

p (X ) = max | X: |        _v          ,

’    i         X i G X X e R k

,                         ,

a,, tions " in (22) take the values received on the basis of

(20). Apply adaptive model

.

Application ^{p (} X ) to (20) allows to find an estimation for maximum an element of vector A ⁿ .

^p " , n = ^a " , n - X p ^U n )    "  = t , b

a

Ф -algorithm of [16] tunings of parameter   " , ⁿ

To decision-making on adequacy of the received estimations apply a domination condition. Consider model

^p " , n    F ⁽ P " , n )

/ " , n   ^a u ^P " U n )   ^{n e} J N

,                        ,

л where " t’ b , "nn there is an upper or lower estimation of norm PУп), P"(Un) there is an estimation for PUn)

.

Define pu-n and check up condition pu’n — Pyn) on P, the basis of an evaluation of indicator /u . For receiving of demanded level of domination correction of current estimations in (20) is required. Apply the approach described in section 2.

The following stage is dependence definition

a tween " and a corresponding element of vector

be A n

.

For this purpose study correlations between P U ⁿ ) and ^{| u i , n |} on all interval of decision-making J ^N .

Two approaches to correction of estimations (20) are possible. The first approach is based on the analysis of a modification of coefficient of structural properties [16, 18]. It is described in [18].

The second approach is based on application of the adaptive approach. In this case as criterion of decisionmaking use indicators

P-/5 t , 5 = P( p . t , 5 - P 5 ( У п )) - P t ,	V n e J N ,	(23)
P -/5 b , 5 = P( p . b , 5 <  P 5 ( У п )) - P b ,	V n e J N ,	(24)
where P t - >  0, P b - >  0 are some	set magnitudes.

After an evaluation (22) apply a ^S -domination condition

^p t , n ^- P ⁽ У п ) >  S 0 <  p ( y n ) ^{- p} _b , n >  5 _y

where ^{P t} ’ ⁿ , ^{P b} ’ ⁿ is model (22) exit, ^{S 0} .

For abatement of sensitivity of algorithm to an operation of perturbations a condition (25) consider concerning the smoothed values of variables. As initial estima-

^a u , n

4 n - 1 ^- Y^P u , n ^- P ⁽ У п ⁾⁾ P ^(U n )’ ⁵⁽ P )e u n > S y , ^a u , n - 1 ,             ^{5 ( u ) e} u , n <  ^S y , (28)

whe r e ^F there is an operator of an average (smooth-

P ing), unn is an average value of an exit of model (26) on interval [0’n], e",n P",n p(Уп), p(Уп) is average value P(Уп) on interval JN , Yu G ^ is the positive parameter ensuring convergence of algorithm,

s(P) =

1, "  = t , _- 1, u = b.

If average operation is not applied, algorithm (28) write as

C t u ,n = C t u , n - 1 ^- ~ u (/ ^ u , n ^- P ⁽ У п )) P ^{( U} n )’

~ _ \У ц , ^{5 u )} e u n > ^S y ’

Y"   [ 0, 5(A)eu, n < Sy ’ where e",n = Pu,n - p(yn) .

Consider properties of algorithm (29) at "  t .

Theorem 3. Let ¹ ^ ⁿ | < ^u . Then the algorithm (29) is a solution of target inequality ¹ e t , ^{n 1} >^ ^y , ^У > > ^ , if

0 <  ~ <  ^2| e t ’ ^{n +} U ^{n 1} t        le t , n\ ^

and number of errors of algorithm

!Рк^ m _ c2S2 ^

S ² = max p (U n ) where ^c - ¹,        ⁿ

U n = l ^ n l

.

The proof of the theorem 3 is similar to the proof of the theorem 2. Similarly receive properties of estimations for case "  = ^b .

Consider an example from section 3 and find an estimation of area ^ A (19) for a vector of parameters in case of an operation of random disturbance ^ n , I U^ 0.3

.

For vector A ⁿ on the basis of (20) and (21) receive a , = 1.35 a _A = 1.07

estimations ^t , ^b . It is an estimations of element a ³, " ^G ""  . They are overestimated, as ^P A n ) = ^1. Let ^a t ^{,0 1.35} , ^a b ,o 1.07. Calculate aver

Fig. 8: Tuning of parameters of model (26)

age values ^P y " ) , ^ U n ) on interval J N . Apply for this purpose procedure of a sliding average and receive sets { P s ^{( y} " ^)}, { P s ^(U " ^)}. Then on the basis of { P s ^{( y} " ^)}, { p ( U )} ■ v v a_t = 1.14 a = 0.9

^{s n} receive estimations ^{t , s} , ^{b , s} .

4,2

P ⁽ У п )

P ( У n ) 3,6

3,0

2,4

1,8

1,2

1,5          2,0          2,5          3,0          3,5

P ⁽ У п )

Fig. 7: The informational portrait showing results of an estimation in

^P У " ), M y n ))

space

Apply procedure of a sliding average and receive ar-

rays ^{P s ( y} " ) , ^{P s (U} " ) . Then on the basis of ^{P s (} y " )

P s (U n )

receive estimations

a _t , s = 1.14

a _b , s = o.9

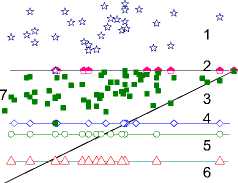
Results of an estimation show on Figure 7. In figure apply following keys: 1 is an output of model with at,0 , 2 is a lower boundary of an output of model with at,0 , 3 is p(y") , 4 is a lower boundary of an output of model with ab,0, 5 there is a lower boundary of an output of a model with  t,s , 6 is a lower boundary of an output of

a, model with b,s . Results of modelling confirm that it is necessary to apply procedure of smoothing of an output

of system y ⁿ to find of estimations of area of parametrical restrictions.

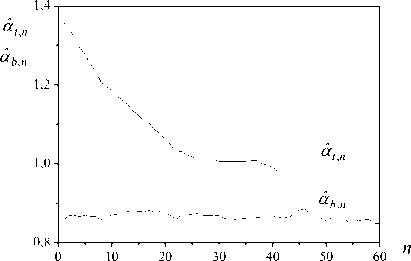
Results of work of algorithm (29) estimations APR

a map on Figure 8. As initial values ц,0 use the estimations received on the basis of (20). To definition of current average value of an output of model (26) apply exponential smoothing. The Figure 9 shows a condition of domination of an output of model (26). The received results confirm also values of indicators (23), (24)

which, accordingly, are equal

5 y = 0.2

P _b = 88%

^ P t

P -

> Pb

= 63%

. Parameter

2, ц = t ,

1.5, ц = b .

Fig. 9: Results of domination of an output of model (26) after tuning of its parameters

For system of identification of parameters ^A construct an informational portrait with map rP £ {p(U")}x{p(У")} .

rP

Find a secant for

γ ( ρ ( y _n ), ρ ( U _n )) = γ_ρ = a ₀ + a ₁ ρ ( U _n )

.

based on use norm (21). Very often to shaping of restrictions apply also norms [20]

^a                          α ˆ

Value ¹ is an initial estimation for ^t in (20). On

γ the basis of parameters of secant ρ define the modified coefficient of structural properties [16, 17]

ρ ( y _n ) - a ₀

s , ρ , n     _{ρ ( Un )      ∀ n ∈ JN}

nn γ ( X ) = ∑ | x i | h ( X ) = . ∑ ^x i ² i = 1                       1 i = 1

,                                              .

Comparison ρ ( X ) and (34) shows that

.

k

Calculate maximal value   ^{s , ρ , n}

κ = maxk s,ρ, n

n

.

А

л

If κ ^t <  α ^t , where α ^t the value received on the basis of application (20), then κ ^t we accept as new estimation α ˆ ^t in (20).

ρ ( X ) ≤ γ ( X ) ρ ( X ) ≤ h ( X ) , .

Hence, use of norms (34) for static system (18) gives the underestimated (pessimistic) estimations (20). To bypass this problem, make the following. Apply as initial norm ρ ( X ) and by means of stated above approaches receive estimations (20). Designate them as

α ˆ b ^ρ ≤ || A n || ≤ α ˆ t ^ρ

.

Generate sets

For decision-making rather κ ^t find p r ognosis ρ ( y ⁿ ) on the basis of model (22). If it is fair ρ ^{t , n >}  ρ ^{( yn )} the upper bound of area Ω ^A is defined. Here ρ ^{t , n ,} ρ ^{( yn )}

ρ ˆ , ρ ( y )

there are average values of variables ^{t , n     n}

Calculate

.

κb = min ks,ρ,n n , ,                                                (33)

κ > αˆ       αˆ and check up condition b b , where b estimation αˆb in (20). If the inequality is fulfilled, κb consider αˆ new estimation b in (20). For decision-making about value κb use described above a rule.

So, the statement is true.

Statement 3. Let for the informational portrait set by Γρ ⊆ {ρ(Un)}×{ρ(yn)} ration             n         n , the secant (30) is re ceived and the coefficient of structural properties (31) is defined. Then values κt,κb satisfying (32) and (33), use as an estimation for αˆt, αˆb in (20), if

ρ ˆ _{t , n} > ρ ( y _n )   ρ ˆ _{b , n} <  ρ ( y _n )

,                                             .

Application of the statement 3 for an example from section 4.3 states the following estimation of area Ω _A = [0.78; 1.22]

• 4.5.    About influence of vectorial norms on an estimation of area Ω ^A

The methods of estimation Ω ^A stated above were

Gv = {kv(Xn), n∈JN}  v=γ,h where

k v ( X n ) =

v ( X n ) ρ ( X n )

.

α ˆ ^v α ˆ ^v

Now define such ^{b , t} that they allowed to cover some area corresponding to average value v ( y ⁿ ) . For this purpose find average values k ^v ( X ⁿ )

N

υ v = k v ( X n ) = ¹ ∑ k v ( X n )

n = 1

.

Receive following estimations for area Ω ^A on the

v ( X )

basis of norm

α ˆ b ^v ≤ v ( A n ) ≤ α ˆ t ^v ,

α ˆ _b ^v = υ _v α ˆ _b ^ρ , α ˆ _t ^v = υ _v α ˆ _t ^ρ

Other approach to an estimation of area Ω ^A in case

γ ( X )      h ( X )

of application of norms      and is described in

• V. Conclusion

The problem of an estimation of area of parametrical restrictions of static object in the conditions of uncertainty on a class of irregular inputs is considered. Advantages and shortages of the vectorial norms applied to description of area of restrictions are noted. Algorithms of an estimation of parameters of area of restrictions are stated. Procedures of the analysis of the data and a deci sion making in offered algorithms are considered. Working capacity of the offered procedures and methods is confirmed by results of modelling.

The majority of methods is based on construction of a field of secants in some space. It is shown that the most adequate estimations of area of parametrical restrictions can be received in case of application of norm

ρ ( X )

Use of other norms gives the estimations, not having practical value. Therefore algorithms of an estimation

Ω                               γ ( X ), h ( X )

of area A in case of application of norms      , should be based on the results based on use of norm

ρ(X) . Criteria of a decision making in case of identifi- cation of restrictions on norms

γ ( X ), h ( X )

are offered.

• [1]    Gagliardini P., Gouriéroux C., Renault E. Efficient Derivative Pricing by Extended Method of Moments. National Centre of Competence in Research Financial Valuation and Risk Management, 2005.

• [2]    Rossi B. Optimal tests for nested model selection with underlying parameter instability. Econometric Theory. 2005, 21 (05): 962-990.

• [3]    Giacomini R., Rossi B. Model comparisons in unstable environments. ERID Working Paper 30, Duke, 2009.

• [4]   Magnusson L., Mavroeidis S. Identification using

  stability restrictions. 2012, http://econ.sciences-po.fr/sites/default/files/SCident32s.pdf .

• [5]    Bardsley J.M. A bound-constrained levenburg-marquardt algorithm for a parameter identification problem     in     electromagnetics,     2004.

4.pdf.

• [6]    Palanthandalam-Madapusia H.J., van Peltb T. H., Bernstein D.S. Parameter consistency and quadrat-ically constrained errors-in-variables least-squares identification, International Journal of Control, Vol. 83, No. 4, April 2010: 862–877.

• [7]    Van Pelt T. H., Bernstein D.S. Quadratically Constrained Least Squares Identification, Proceedings of the American Control Conference, Arlington, VA June 25-27, 2001: 3684-3689.

• [8]    Corrêa M.V., Aguirre L.A., Saldanha R.R. Using steady-state prior knowledge to constrain parameter estimates in nonlinear system identification. IEEE transactions on circuits and systems—I: Fundamental theory and applications, 2002, 49(9): 1376-1381.

• [9]    Chadeev V.М., Gusev S.S. Identification with restrictions. determining a static plant parameters estimates, Proceedings of the VII International Conference “System Identification and Control Prob-

  lems” SICPRO 'OS Moscow January 28-31, 2008.

V.A. Trapeznikov Institute of Control Sciences. Moscow: V.A. Trapeznikov Institute of Control Sciences, 2012: 261-269.

• [10]     Chia T .L., Chow P .C., Chizeck H.J. R ecursive parameter identification of constrained systems: an application to electrically stimulated muscle, IEEE Trans Biomed Eng., 1991, 38(5): 429-42.

• [11]    Wen-Ming Shi. Parameter Estimation with Constraints Based on Variational Method, Journal Marine. Sci. Appl. 2010, 9: 105-108.

• [12]    Vanli O.A., Del Castillo E. Closed-Loop System Identification for Small Samples with Constraints. Technometrics. 2007, 49(4): 382-394.

• [13]     Hametner C., Jakubek S. Nonlinear identification with local model networks using GTLS tecniques and equality constraints. IEEE Trans. Neural Netw. 2011, ;22(9): 1406-18.

• [14]    Mead J.L., Renaut R.A. Least squares problems with inequality constraints as quadratic constraints. Linear Algebra and its Applications. 2010, 432: 1936-1949.

• [15]    Mazunin V.P., Dvojnikov D.A. Parametrical restrictions in nonlinear control systems of mechanisms with elasticity. Electrical engineering. 2010, 5: 9-13.

• [16]    Karabutov N.N. Adaptive system identification: information synthesis. URSS, Moscow, 2006.

• [17]    Karabutov N.N. Structural identification of systems: analysis of informational structures, URSS: Book house “Librokom”, Мoscow, 2009.

• [18]    Karabutov N.N. Structural identification of static objects: Fields, structures, methods, URSS: Book house "Librokom", Мoscow, 2011.

• [19]    Karabutov N.N. Structural identification of a static object by processing measurement data. Measurement Techniques, Springer US. 2009, 52(1): 7-15.

• [20]    Lancaster P. Theory of Matrices. Academic Press, New York, 1969.