Идентифицируемость высокотемпературных псевдоожиженных слоев

При моделировании процессов в высокотемпературных реологически сложных (дисперсных и пр.) системах описание гидромеханики потока требуется дополнить учетом тепломассопереносных свойств объекта, фазовых превращений в нем и пр. Так, при экспериментальной отработке топок с кипящим слоем по измерениям температуры и составу газовой фазы по высоте слоя определяются такие величины как эффективная энергия активации процесса горения Е , относительный размер горящей частицы 1 / ^, коэффициент диффузии К . Для разрешимости задачи необходимо, чтобы между множеством измеряемых параметров и состояния, расширенным вектором оцениваемых характеристик, существовало взаимно однозначное соответствие [1].

Исследуем идентифицируемость математической модели (4.14 в [2]), включающей дифференциальные уравнения баланса окислителя в непрерывной и дискретной фазах и баланса энергии для ожижающего агента и твердой фазы. В модели проведем учет неоднородности генерации тепла на поверхности частиц топлива и поглощения окислителя по высоте слоя у путем введения нелинейной функции: степенной, экспоненциальной и пр., одним из вариантов которой является зависимость с коэффициентами at (i —1...4) как в [2]. Заметим, что чем большее число неизвестных параметров включает функция, тем с меньшей точностью они могут быть оценены из условия минимума критерия качества ввиду его овражности в пространстве этих величин и смещения минимума вдоль оси оврага при прочих равных условиях, но с другой стороны с широким набором характеристик функция более корректно аппроксимирует поведение системы. Выбор оптимального представления исходных и пр. данных входит в круг задач параметрической идентификации [1]. Проверим достаточные условия глобальной биективности отображений в терминах якобиевой матрицы. Математическую модель кипящего слоя представим в виде:

dy dy   Uю^1 TV -1

^2 +     (1 + U_x и + U_ny² ^ + РП(П₃ -£70 ;

Ъ_Рпуз-иУ^ = и5;

dydy dU< — amf (V\

^4   .

^9^10

— = ———(1 + UX3y + С^дУ J+ФВ dy Ug 4'

dy        dy UgUXo

^8 __Q. dUg _Q ^ _{= Q}. dU_u _^ dU_n dU_x3 ^ dU_{u = Q} dy dy dy dy ’ dy ’ dy ’ dy

Краевые условия для системы (1):

dy 2 dy 5 UXti ’ dy '

В (1), (2) приняты следующие обозначения (см. также [2]):

UX=C; U2= — ; U3=C ; U4=©g; U5—^< U6=©; U7—; dy        *                 dy                 dy

Ug = E; Ug = — ; U_Xq = К; (7) ] = cq ; U_X2 — or2 ’ ^13 ^{= a}3 S ^14 — <^4 • Ф

В системе (1) вектор состояния U математической модели расширен включением вектора неизвестных параметров Ug-UX4, благодаря чему задача идентифицируемости сведена к задаче наблюдаемости вектора начальных состояний системы (1). В краевых условиях (2) не определены начальные условия для Ug-UX4, т.е. неизвестны семь условий для системы (1). Возможность оценивания неизвестных величин из измерений температуры 0g по высоте слоя определяется из анализа матрицы отображений J [1], которая в настоящем случае в каждой строке содержит п

элементов вида

5й

OXj

'6©g^

, где п - число неизвестных параметров х \п = 7 - для модели

(1)), к, j - номер строки и столбца (90 _g /йху-для первой строки).

Функции чувствительности в матрице находятся из решения системы уравнений для функций чувствительности с нулевыми начальными условиями [1]. Для определения системы уравнений для функций чувствительности следует продифференцировать систему (1) по неизвестным параметрам x{E,(p,K,a_t ) и сменить порядок дифференцирования в левой части уравнений. Далее исходная система уравнений (1) и система уравнений для функций чувствительности интегрировались совместно по высоте слоя у с шагом Ду, принятым постоянным в связи с необходимостью вычисления для остальных строк матрицы Якоби производных по у от функций чувствительности. Так, для функции чувствительности 90 _g ! 6Е можно записать систему уравнений: d (St — -- =-—,                             (4)

dy ( dy J BE где U = [[/j ... t714]T; f = [/] ... /14]T в системе dU / dy = f(U,x,y), с нулевыми начальными условиями, которые получаются дифференцированием краевых условий системы (I) по Е . Система уравнений чувствительности для 50 g /ЭЕ -SU^ /SUg*, где Ug* - начальное значение

Ug, имеет следующий вид:

d ( 8U^ dy^SUg*,

8U2 . SUg* ’

d ( SU₂ А -1 dy^dUg*) и_хое_х

”—7^2 +    ■ (1 + U_x 1У ⁺ ^12T²^² + РП(и₃ - U_x)

X

5^10 ,    1__ 1 8U_X

8Ug* U^x[N-ldUg*

+ u y+u y^

Ug               ’ ЭЕ Ug

au, ftgp aun 3au„V p^i         Ц aut (su3 au

U1--1--У--■ у ------- Ui 4--11 4- Ui 1 У 4- U17 У /--г Г11--- аиил - р4 эиз

8U_X Y d ( dU₄

SUg* dy xSUg*

8U5 .

8Ug* ’

dy\cUg*)      \8Ug*

8U\3 SU g*

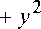
8Ug* v

-qm§\U_X3y + ^u_X4y )—— + du §*

1    8U4 U₄ SUg U₄ 6U_X0

+ ФВ--— - ФВ —— --— - ФВ =--—;

^9^10 ^8U&*      ^и9^иФ ^8U&*     U₉U^₀ 8Ug*

Физика

d dy

' ЭЦ₆ Л_ dUg , _VBU₈* j 9U§*

d

8U_n I        1    ^8U4       ^4   ^8U9       ^4   ^8U\0

--- = -ФВ-------- + ФВ-----— + ФВ-----— ;

dy^BU^

d

9U%

dy 'JUy

^9^10 8U%*

’ dy \_9U8*,

UgUw 8U^

= 0

^10 ’ dyXBU^,

= 0;

dy\3U₈* J ’

d 0U_n dy \BU₈*,

0; d(8Ux3" dy \^Ви8* ,

_0; ^ 5^14 ’ c/y^dt/g*

= 0.

Система уравнений (5) решается при граничных условиях:

₀.    =  ^- = 0- ^- = 0- ^{8U2     1 8Щ} • ^8Щ

У ' ди8* ’ 8U8*    ’ ди8* ’ 5U8* k(N-1) 8U8* ’ 9U8*’

5^9 _0 ^ = 0;^Н          ^13. = 0. ^1± = 0.

8U8*     8U8*     9U8*     9U8*     9U8*9U

Рассмотрим вычисление элементов первого столбца матрицы наблюдаемости J. Так, эле-

9 (8®g ) 9 ( BU6 )

мент — ---- = — ---- определяется разностным методом (например, для наглядности

By 1^ BE J 9y\_ 9U₈* )

приведем схему с точностью О(Ау2)):

9 р^б 8y\.BU₈* Р

2Ау

т.е. применяется простая алгебраическая операция над решениями системы (5). Следующие элементы первого столбца находятся аналогично, например, с точностью О(Ау2):

5² ( 9U₆ )

dy2 Р^8* ; 1

(9U6)     (9U6

8*)_/+1    \9U₈*

А)-2

, f atV / P^s* >

^- + O(Ay2);

9^т (9U₆ 9у^т\^8и8* J

9^т-х ( 9Ц₆ Л 9^т~^х ( 9U₆ )

2Ау

^g 8иб

Система уравнении для определения элемента —— = - 7 -■ —г имеет вид: 9ср 9\).IU()*)

d (dUA BU₂ , dyV^ 9ф J 9ф '

d ( 9U₂ dy V Вф

"— ——7^2 ⁺”™^ ⁺ Uny ^{+ u}_ny²\^J\ +РП(и₃ -U_x) U_Xq£_XV^N-^{X U}9                              .

BU\o ~^      1 BU 2

⁸⁽p и_xos_x p-^{1 8(}p

+ P\^D^ + U_x iy + U_x2y² p + ^ | 1 + . ¹¹ T + Uq ( Вф

WL        2\8U\

——\^ + Uxxy + Ux2y —

U 9                 оф

*РП\

BU3 Вф

аих Вф

x

^8un Вф

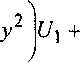
d (SU₃\     (8U₃ dU_x) d SU 4) SU5

dy ( Эф J      ( 9ф   Эф У dy\ Эф ) Эф '

d(9U₅A V           ₂W / dl/_{I3 2} 5^14

¹   9U₄ Уд 9Ug

+ ФВ-----— - ФВ ———

^9^10 ^бф

U^U;0 9<Р

_ФВЛ^821™.

а 8и6у ди7, dy у Эф ) 9ф ’ dUu7\ фВ i эи4 dy^ Эф J ^9^10 9ф

U^ SUg , AD U4 dUX0

(/9^io        ^^o 9cp

d(9U^_ d(dUg\ ^.dUu^   d(8Uxy dy\ Эф j dy\ Эф J dy{ Эф J dyy Эф )

dy\ Эф )   " dy\ Эф )   ' dy\ Эф )’

A 9U2     1 ЭЩ 8U3 A Эи5"dU y = 0: —=------—1; —^- = 0; —- = 0;--^- = 0;

Эф k(N -1) Эф Эф Эф Эф

SUq     dUg 1

—— = 0; —=—- = 0,(z = 10,. ..,14);

Эф     Эф    дУ Эф dyy Эф ) dy\ Эф ) dyy Эф )

Остальные элементы второго столбца матрицы вычисляются разностным методом аналогично элементам первого столбца. Системы уравнений для функций чувствительности Э©₈ / ЭК, 90g !Эа_х Ц = 1,...,4) получаются аналогично. Функции U, (i = 1,...,14), входящие в систему уравнений (4), определяются из решения системы (1).

В терминах Якобиана для рассматриваемого процесса [2] установлены локальная и глобальная идентифицируемость [1] системы по эмпирическим данным и пригодность модели для описания рабочих процессом в высокотемпературном псевдоожиженном слое. При наличии в модели четырех параметров, описывающих нелинейности по высоте слоя, a, (z =1...4) при различных видах задаваемых функций ранг матрицы J был равен 7 и она являлась P-матрицей. Подобный анализ важен, прежде всего, при слабой наблюдаемости исследуемых эффектов и свойств и предпочтительно его обязательное применение, особенно в многопараметрических задачах. Построенные функции чувствительности используются в дальнейшем при нахождении ковариационной матрицы ошибок оцениваемых параметров по матрице ошибок измерения, изучении точности математической модели и оптимальном планировании эксперимента.

Работа выполнена при частичной поддержке РФФИ-Урал (№ 07-02-96016).