Идентификация неньютоновского поведения жидкометаллических систем

L4L"p/q = 2K(p-p_oy,                          (1)

Т Т Т т n           7 к² £^0„ Н/2)

Ь = Ьх*Ьэ , Lx= -2vMB, L2 = 4--У—” , -, 121 p 2 Я V Й где p = Rsjkiv, М = рз^Н, 02-p2-k/v\ k = p*iq, р = 8!т, Po=8o/tq, q = 2nlr, q0=27r/TQ; i = V-T; Ji - функции Бесселя первого рода / -го порядка; М - масса среды в тигле высотой Н и радиусом R; Lx и L2 - функции трения на боковой и одной торцовой поверхности; р - коэффициент затухания и q - циклическая частота колебаний; 80, т0 - 8, г при М = 0; рп - корни уравнения Jx(pnR) = 0. Введем также безразмерные комплексы, описывающими основные условия опыта: A = MF^ /2К и ^=R!d, где А - отношение моментов инерции среды в тигле и пустой подвесной системы К; d=-jv/q0 - естественный масштаб длины, толщина погранслоя.

Выделим наиболее важные моменты в чувствительности вязкости ньютоновской среды к наблюдаемым в эксперименте параметрам [1], в характере поведения параметров колебаний в процессе затухания для неньютоновских сред и особенностях параметрической идентификации таких систем, основах аналитического метода определения нелинейных свойств и пр. [2].

Для ньютоновской среды безразмерный период 2 = т/гд уменьшается с ростом £₀^в основном при <₀ 6 (2; 12), а поведение 8 зависит от ^о^: при ^о > ^_Og с ростом £₀ 8 падает, а при £₀< 5о₅ ~ растет [1]. Для длинного тигля ^₀^ ~ 4,3, а с уменьшением Н этот пик 8 = 5(£о) смещается в сторону больших 5о • Тогда в районе максимума чувствительность v к 8, а, следовательно, и ошибка в v от ошибок измерения 8, очень высока, также как и к ошибкам в г при ^0, близких к нулю и высоких £₀ • При снижении А зависимости 8 и 2 от ^о становятся более пологими, т.е. чувствительности, как и ошибки, вносимые одной и той же точностью измерения, растут. Слева от ^_g - сильновязкое приближение, при £₀ >10 - слабовязкое, а интервал между ними отвечает промежуточной вязкости. С усилением упругих свойств число экстремумов на зависимостях г и 8 от £q растет, что определяется отношением длин вязкой и упругой волн.

Поведение реостабильных сред можно описать в терминах эффективных (усредненных, например, по периоду) значений ^_Оэф = ^а Для вязкоупругих сред аналогично вводится понятие эффективного времени релаксации и т.д. [2]. В частности, для нелинейно вязких сред эффективное значение £_Онв = £₀ / л[ьВ ^, где D - усредненная по внутренней поверхности тигля скорость сдвига D, b и т - постоянная и показатель степенного реологического закона, и ^Онв^ ~ 4,3.

С ростом номера колебания N амплитудное значение D падает, поэтому для дилатантных сред (w > 1) <_Онв растет, а для псевдопластичных (т <1) падает, и соответственно изменяются 2 и 8 . Так, при т > 1 если £о_нв^ПР^И ^ = 1 находится в слабовязкой области, то 2 и 8 уменьшаются, а если сильновязкому - 8 = 8(N) проходит через максимум. Для вязкопластичных сред (предел текучести сгд * 0) при некотором D и ниже твердое ядро, где сдвиговые напряжения не 1/2 превышают сг₀, заполняет весь тигль в любой момент времени и 8 ~ Зц , 2_ТВ ~ (1 + Л) . Для металлических образцов в вискозиметре в зависимости от величины и характера действия межчастичных сил характерен любой из этих типов, в т.ч. и с эффектами памяти. В каждом конкретном случае причины одного и того же реологического поведения могут быть различны.

Свойства нелинейных жидкостей определим из условия минимума функции качества, являющейся критерием соответствия экспериментальных и расчетных данных:

где у - номер точки измерения (например, N ); т_эф - эффективная вязкость (например, для нелинейно вязкой среды У_эф^. =ЬВ^ (6 =v6), для бингамовской среды т_эф^. =vc(l + 5/Dy))(cr₀=vcd^:); v - вязкость, определенная по (1); v = ^vj jL, L - число измерений;

s (R                  0           ^>

5у =---^J- --- Шг-HVdr^R WR^dz RH^SR¹^         -н )

где D^ и D2 - модуль zip -й и rip -й компонент тензора скоростей деформации в цилиндрической системе координат (r,p,z:r = 0 - на оси, r = R - на боковой стенке, z = -H- на нижнем и z = 0 - на верхнем торцах); Sj - коэффициент усреднения по т; первый и второй интегралы в (3)

I^lReGOl.^-^a^th^

п

nR 2Мп^

(ji^HoG^-Jo^^

1₂ =|Ке(/₂)|, /₂ = -(RHiPq_ajJ₂{pyj_x(P) + R^

И an = 21да^/0„ -1)/(ди70(//й/?)), 0„ =Д-k/v, J^z^n: 1 Jcos(zsin0-I0yi0, 0

E/(z) = ^-1 Jsm(Z^-zsin^, H0(z) = -E0(z), H1(z) = 2/^-E1(z) ([142] в [2]); 0

Е/, Н/ - функции Вебера и Струве /-го порядка (/ - целое положительное число или нуль); aj - начальное угловое смещение тигля для каждого j ( a_y=1 = а^~ 0,1).

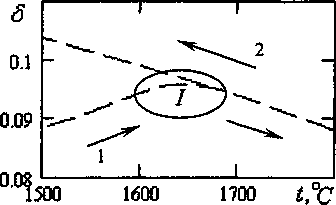
Рис. 1. Температурная зависимость 8

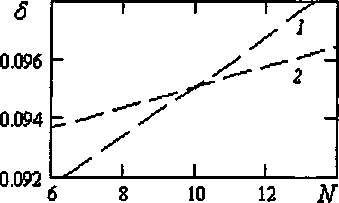
Рис. 2. Зависимость 8 = S^N^ : 1,2 - номера точек

Далее размерные величины даны в системе СГС (температура t в °C), данные сглажены, выводы выполнены при качественной воспроизводимости особенностей в различных экспериментах. Моделированием установлено отсутствие влияния на результаты по «у переходных процессов при условиях и алгоритме опыта, когда движение инициировалось в вынужденном режиме.

Результаты и обсуждение. Несмотря на достаточно широкий разброс данных по декременту, общие тенденции в его изменении в процессе затухания колебаний проявлялись достаточно отчетливо. Свойство неизосинхронности наиболее существенно после расплавления материала и угасает по мере роста t . В этой связи интерес представляют эксперименты, когда образец длительное время находится при одной и той же t , а его свойства (а вероятно и реологический тип) изменяются, что проявляется в наблюдаемых в опыте параметрах колебаний. Здесь следует учитывать и факторы, упоминаемые еще Швидковским Е.Г. [1], например, возникновение пленок на поверхности, что изменяет расчетную зависимость от формулы для одного торца до таковой для двух, влияние плоских движений и пр. вопросы теории и техники эксперимента. Эффекты возникали и в процессе опыта, особенно если на температурных зависимостях вязкости имелись аномалии.

В ряде случаев зависимость 5 = ^(У) носила колебательный характер, что говорит о наличии упругих свойств. Такое характерно для линейных вязкоупругих систем в переходных процессах (здесь не проявляющихся) или при наличии дополнительно пластичных свойств. В пользу последнего говорит и то обстоятельство, что £о_эф с ростом N изменяется, а наличие минимумов 5 = 8(N) обеспечивается таковыми на зависимости 5 = £(£_Оэф) Д^ля вязкоупругих сред. Для линейной среды т и 5 в регулярном режиме постоянны, а свойства оцениваются из уравнения: для вязкой среды - по [1] (например, (1)), а вязкоупругой - в терминах комплексной вязкости [2]. -Метод затухающих колебаний малоэффективен для измерения линейных вязкоупругих свойств [2], поэтому для уточнения упругого характера расплава комплекс экспериментов должен включать измерения в вынужденном режиме по зависимости Клеймана Р.Н. ([221] в [2]). Заметим, что для линейных сред т и 5 не зависят от «₀, а АФХ - от амплитуды вынуждающей силы.

Отмеченную систему поведения можно пояснить следующим образом. Разогретый металл демонстрирует вязко(псевдо)пластичное поведение (например, [98] в [2]), в общем случае с наличием упругой составляющей в уравнении состояния. В процессе плавления металла псевдо-пластичный характер остается, в т.ч. из-за присутствия в гетерогенной области кристаллов твердой фазы, но его свойства принимают значения по порядку более близкие к жидкому состоянию. По мере роста t происходит перестройка структуры в таковую, отвечающую ньютоновской среде (упругие и пластические составляющие теперь выражены хуже), определяющую роль начинают играть иные механизмы. Превращения в процессе опыта, наличие в гомогенной среде нерастворимых и растворимых примесей и пр. приводят реологический тип, например, к дилатантному. Пример 1. Условия эксперимента: Jo~ 0,006, го~3,О9; г-3,18, R-0,68; % = Н/R-3,4; А -0,12. В опытном образце в районе точки ветвления (область I на рис. 1) зависимости 5 = 8(N) несколько колеблются около среднего значения, возрастающего с ростом N. Довери- тельные интервалы для значений б для верхней и нижней кривых пересекаются только вблизи точки ветвления. Будем исходить из монотонного характера 8 = 6(N) (рис. 2); рассмотрим точки, отвечающие ветви 2: 1 - t = 1670 и 2 - 1725. При отдалении от области I колебания приближаются к изосинхронным. Для точки 2, проходимой в опыте перед точкой 1 и отвечающей более высокой I, зависимость б = 6(N) более пологая (что качественно характерно и для случая равных свойств одного типа среды), а усредненные по всем N значения б и v ниже (слабовязкая область: £Оэф ~ 10, для первой точки £Оэф ниже; v ~ 0,009 ). Значения параметров колебаний для нелинейных сред зависят от а0 и при измерении aj при различных а0 получаются различные б (для точек 1 и 2 разница Да0 <1%). Для t ~ 1675 ветви 1 ситуация с 6 = 6(N) близка к таковой для точки 1, а при их совмещении с учетом а0 (Да0 <5%) данные можно считать совпадающими. Целевая функция (2) имеет криволинейный овраг на плоскости (т,Ь) и ввиду слабого изменения б от N широкий диапазон значений / на оси оврага близок к минимальному, что осложняет процедуру корректной оценки. Для лучшей наблюдаемости свойств следует перейти к более низким £0 (целесообразно в сильновязкую область), % или высоким А, а оптимальные условия выбираются в рамках матрицы Якоби [2]. Псевдопластичные свойства выражены сильнее вблизи ветвления кривых б = 6(f): т ~ 0,74 (6 ~ 0,86 ) для точки 1 и т ~ 0,88 (6 ~ 0,93 ) для точки 2 (при а0 ~ 0,1), что говорит о структурных превращениях в этом диапазоне I. На рис. 3 отмечены кривые течения в диапазоне D, проходимом в эксперименте. Для каждого опыта он может быть разный (в т.ч. разное число периодов L) и это еще один из путей получения иного б .

Пример 2. В экспериментах с железом после расплавления наблюдалось ярко выраженное псевдо(вязко)пластичное поведение (рис. 4), пропадающее с ростом t (v ~ 0,199, опытные условия близки к примеру 1). Оценивание свойств по (2)—(4) дает т ~ 0,65 и Ъ ~ 0,43, а если использовать бингамовскую модель, то ст ~ 0,05 и с ~ 0,65 (минимумы функций / имеют одинаковый порядок). При этом на оси оврага на плоскости (с, ст) возникают локальные минимумы, выраженные слабее, что может быть обусловлено ошибками и низкой наблюдаемостью при этих условиях пластических эффектов. Таковой наблюдается в случае, когда пластическая вязкость в области, где существует течение, имеет такой же порядок (~ 5 • 10~³ ), как и ньютоновская при более высокой температуре, что свидетельствует о erg * 0, стремящемся к нулю с ростом t . Условия, возникающие в тигле [2], позволяют обнаружить малые ст₀, не проявляющиеся в иных методиках. Наличие ст₀ изменяет г и б, но для корректного решения прямой задачи реометрии ввиду обратной величины чувствительности требуется проведение специальной оптимизации и следует, например, увеличить продолжительность измерений в каждом опыте, т.е. L.

Нелинейное поведение возникало и при уменьшении /, например, в экспериментах с жидким алюминием (рис. 4 для t = 630; А ~ 0,056, ^_Оэф при работе в слабовязкой области ~ 14 и в сильновязкой  2,2 ), что может быть обусловлено в т.ч. проникновением окислов в расплав и возникновением гетерогенной системы. Данные, как и для Fe, отвечают промежутку между солидусом и ликвидусом, но нелинейность носит дилатантный характер. На подобное поведение могут влиять схемы фазовых переходов, начинающихся при больших R . Расчеты выполнены для приведенного для всех температур г, в то время как ниже ликвидуса период резко возрастает, как и чувствительность к ошибкам в нем. В обоих случаях условия отвечают сильновязкой области, что определяет выбор одного из двух решений по (1). Об этом свидетельствуют в т.ч. более низкие значения 5, чем в соседнем измерении и их тренд в процессе опыта. Модель с т > 1 обнаруживалась в ряде расплавов и выше ликвидуса, а с ростом / показатель т -»1.

Пример 3. Пусть эксперименты начинаются при близких ад с расплавами одинакового реологического типа и свойствами (близкие содержание примесей, структура и пр.). Покажем, что не-учет даже незначительного изменения б при изменении N (обусловленное слабо нелинейным типом, например с т = 0,85 ) может приводить к ошибкам и следовательно противоречиям в данных по вязкости при использовании различных установок в предположении ньютоновского характера течения. Это особенно характерно для низких температур из исследуемого интервала.

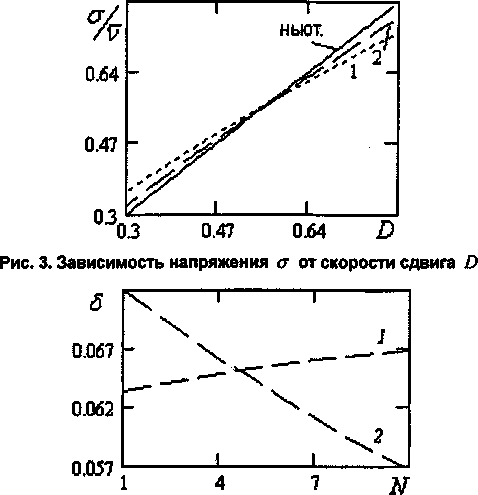
Рис. 4. Зависимость 8 = 8(^ : 1 - для А1,2 - для Fe

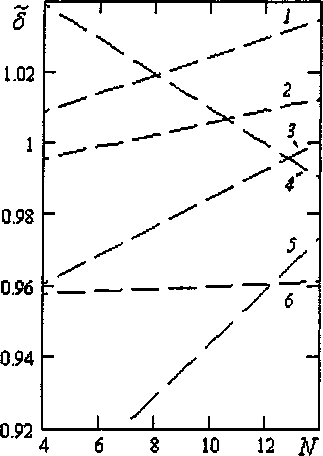
Рис. 5. Зависимости 3 = к8(№) : 1 ... 6 - номера точек;

1- №30,2 - 45,3-15,4 - 34,5 - 7,6-150

Для наглядности примем приближение длинного цилиндра (при 5q ~ 0 ) в терминах безразмерных параметров (В, b и пр.) [2], моделирование закона колебаний [2] выполним для «о ~ 0,11 (с учетом переходных процессов). Значение 6 = 0,7 принято исходя из bD^m~^ -1 -> min в диапазоне рабочих 2); £оэф ⁼ £оФ» ^гД^е ^0 фиксировано. По традиционной методике оценим <р - величину, которая для ньютоновской жидкости при различных опытных условиях была бы константой, для точек: А = 0,1, £₀ = 10 (1); 0,2, 10 (2); 0,01, 10 (3); 0,1, 20 (4); 0,05,15 (5); 0,075, 2 (6). Получаем: ^7 ~ 1,08 (1); 1,07 (2); 1,31 (3); 1,18 (4); 1,79 (5); 0,96 (6), т.е. результаты, например, по (1) и (5), часто встречаемых в опытах, отличаются в среднем на 50%. Ошибки в иных параметрах к тому же будут давать еще более значительные отклонения. Заметим, что относительное изменение вязкости в 2 раза выше, чем изменение £q • Высокие ошибки в параметрах установки и колебаний и различная чувствительность вязкости к ним при различных А и £₀, конечно, также могут изменять оценку v и для ньютоновской среды. Но корректный учет в рамках [1] позволит выделить их из ошибок, описанных здесь, что может служить критерием нелинейного поведения.

Заключение. Итак, продемонстрированы возможности экспериментальной идентификации реологического типа расплавов в общем случае как нелинейно вязких жидкостей, что в свою очередь позволяет получить новую информацию о физико-химической природе этих труднодоступных для экспериментального изучения сред, а также выполнить рекомендации для производственных целей. Подобный подход, как указывалось в [1], «открывает возможность связать кинетику процесса затвердевания сплава с его вязкостными свойствами» и будет полезен при изучении влияния и механизма удаления из исследуемых систем примесей, структурных особенностей в сплавах, проверки согласованности данных и пр.

В работе использованы экспериментальные данные, полученные в лаборатории исследования физических свойств расплавов УГТУ-УПИ. Неоценимую помощь в ее проведении оказали Вьюхин В.В., Тягунов Г.В., Барышев Е.Е., за что авторы им весьма признательны.