Идентификация параметров и управление в математических моделях иммунного ответа
Автор: Русаков С.В., Чирков М.В.
Журнал: Российский журнал биомеханики @journal-biomech
Статья в выпуске: 2 (64) т.18, 2014 года.
Бесплатный доступ
Цель работы заключается в численном решении задачи дискретного управления иммунным ответом в условиях с неполной информацией. Задача дискретного управления иммунным ответом описана нелинейной системой обыкновенных дифференциальных уравнений с запаздывающим аргументом. Условия с неполной информацией означают, что значения параметров неизвестны, а их оценка корректируется по мере поступления новых экспериментальных данных. Для решения этой задачи предложен алгоритм, позволяющий в рамках математической модели иммунного ответа одновременно строить управление и идентифицировать параметры. Алгоритм строится на основе метода Монте-Карло. Рассматривается управление при острой форме инфекционного заболевания. Идентификация параметров модели проводится по значениям переменных инфекционного процесса. С помощью предложенного алгоритма проведена идентификация параметров базовой математической модели инфекционного заболевания, а также построена программа лечения, основанная на реализации иммунотерапии, которая заключается во введении готовых иммуноглобулинов или донорских антител. Управление выбирается из множества кусочно-постоянных на рассматриваемом отрезке функций. Представленные результаты основаны на имитации экспериментальных значений. В качестве цели управления выбрано обеспечение в некотором смысле «идеального» иммунного ответа, отвечающего высокой стимуляции иммунной системы при отсутствии запаздывания в реакции на заражение. Для этого необходимо динамику антигенов вывести на желаемый режим. Проведено сравнение управления в условиях с неполной информацией с управляющей функцией, построенной с заданным набором значений параметров. Показано, что управление в условиях с неполной информацией лишь незначительно отличается от «идеального» управления. Рассмотренный подход может быть использован для построения различных биомеханических моделей.
Идентификация параметров, метод монте-карло, математическая модель иммунного ответа, дискретное управление, иммунотерапия
Короткий адрес: https://sciup.org/146216140
IDR: 146216140 | УДК: 519.622.2
Текст научной статьи Идентификация параметров и управление в математических моделях иммунного ответа
Математические модели иммунного ответа, широко используемые для исследования динамики иммунной защиты организма при инфекционных заболеваниях [1, 3–7], представляют собой, как правило, нелинейные системы обыкновенных дифференциальных уравнений и содержат большое количество
Русаков Сергей Владимирович, д.ф.-м.н., профессор кафедры прикладной математики и информатики, Пермь
Чирков Михаил Владимирович, аспирант кафедры прикладной математики и информатики, Пермь параметров, которые характеризуют иммунный статус организма и свойства антигена. Оценка параметров системы уравнений по клиническим данным позволяет моделировать динамику заболевания у конкретного человека, а также строить прогнозы течения и исхода болезни. Поэтому одна из важнейших задач в этой области заключается в идентификации параметров моделей по данным наблюдений за фазовыми переменными. С помощью оценки параметров можно моделировать управление иммунным ответом и строить программы лечения для конкретного пациента. На практике, как правило, можно измерить значения некоторых фазовых переменных в определенные моменты времени. В связи с этим актуальна разработка эффективных методов идентификации параметров моделей, позволяющих строить управление в процессе идентификации.
Базовая модель инфекционного заболевания
Наиболее общие закономерности функционирования иммунной системы при инфекционных заболеваниях отражены в базовой математической модели инфекционного заболевания, предложенной Марчуком в 1975 г. [5]. Фазовыми переменными модели являются следующие характеристики заболевания: V ( t ) – концентрация антигенов в пораженной части органа-мишени; C ( t ) – концентрация плазматических клеток; F ( t ) – концентрация антител в крови; m ( t ) – доля разрушенных антигенами клеток органа-мишени. Базовая модель инфекционного заболевания представляет собой нелинейную систему обыкновенных дифференциальных уравнений с запаздывающим аргументом:
dV
— = в V - Y FV , dt
— = a£( m ) F ( t - t) V ( t - t)0( t - t) - p ( C - C * ), dt
dF
— = pC - nYFV - P fF, dt dm
-Г = ° V — Pmm dt с начальными условиями
V (0) = V o, C (0) = C 0 , F (0) = F o, m (0) = m 0. (2)
Биологический смысл параметров модели представлен ниже. Непрерывная невозрастающая неотрицательная функция ^ ( m ) учитывает нарушение нормальной работы иммунной системы вследствие значительного поражения органа. Пусть m * -максимальная доля разрушенных антигенами клеток, при которой еще возможна нормальная работа иммунной системы. Тогда функция ^ ( m ) может быть представлена следующим образом:
^( m ) = <
1, m - 1
,
I m - 1
0 < m < m * , m * < m < 1.
Функция Хевисайда 0 ( t ) определяется по формуле
0( t ) =
f l
<
при t > 0,
0 при t < 0.
Параметры базовой модели инфекционного заболевания:
|
Параметр |
Биологический смысл |
|
β |
Константа скорости размножения антигенов |
|
γ |
Коэффициент, учитывающий вероятность встречи антигенов с антителами и силу их взаимодействия |
|
α |
Коэффициент стимуляции иммунной системы |
|
µ c |
Константа скорости естественного старения плазматических клеток |
|
ρ |
Константа скорости производства антител одной плазматической клеткой |
|
η |
Константа расхода антител на нейтрализацию единицы антигена |
|
µ f |
Константа скорости естественного разрушения антител |
|
σ |
Константа скорости разрушения клеток органа-мишени антигеном |
|
µ m |
Константа скорости регенерации органа-мишени |
|
C ∗ |
Предсуществующий уровень плазматических клеток |
|
τ |
Время, необходимое для формирования каскада плазматических клеток |
Модель (1) описывает общие закономерности, присущие всем инфекционным заболеваниям. Инфекционное заболевание рассматривается как конфликт между патогенным размножающимся возбудителем болезни и иммунной системой организма.
В результате исследования базовой модели инфекционного заболевания выделены качественно отличающиеся друг от друга типы решений, которые интерпретируются как формы протекания болезни (субклиническая, острая, хроническая, летальный исход). Состоянию здорового организма соответствует стационарное решение
V 1 = 0, C 1 = C ∗ , F 1 = ρ C ∗ = F *, m 1 = 0. (5) µ f
Вид решения однозначно определяется начальными условиями и значениями параметров, которые получили название иммунологического статуса организма. Зная значения параметров модели, можно строить прогнозы течения и исхода болезни для конкретного пациента, а также давать рекомендации по выбору лечения. В связи с этим возникает необходимость в решении задачи идентификации параметров модели по клиническим данным.
Для вычислительных экспериментов модель (1) была приведена к безразмерному виду:
dv
= a v - a fv, dt ds dt
= a 3ξ( m ) f ( t - τ) v ( t - τ)θ( t - τ) - a 5( s - 1),
df = a 4( s - f ) - a 8 fv , dt
dm
= a v - a m , dt 6 7
где ν , s , f – относительные концентрации антигенов, плазматических клеток и антител соответственно, v = V / V m , s = C / C * , f = F / F * ; V m - некоторый масштабный множитель для концентрации антигенов, например, биологически допустимая концентрация антигенов в организме.
Моделировалась ситуация заражения здорового организма малой дозой антигенов, поэтому начальные условия задавались в виде
v (0) = v 0 , s (0) = 1, f (0) = 1, m (0) = 0. (7)
Для идентификации параметров рассмотрим течение острой формы заболевания, которая характеризуется быстрым ростом концентрации антигенов, выраженным иммунным ответом и резким в силу этого спадом количества возбудителей заболевания до значений, близких к нулю, что понимается как выздоровление.
Значения параметров модели, характеризующие острую форму заболевания, взятые из работы [5], приведены ниже.
ν 0,0014 0,0012 0,001 0,0008 0,0006 0,0004 0,0002
0,02
0,015
0,01
0,005
t , сут
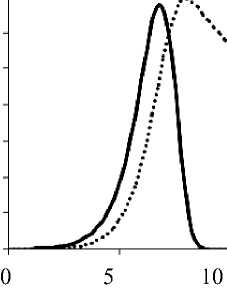
Рис. 1. Динамика переменных инфекционного процесса
На рис. 1 представлена динамика переменных инфекционного процесса при острой форме заболевания. Изменение концентрации антигенов изображено сплошной кривой, а доля разрушенных антигенами клеток органа-мишени – пунктирной. Как видно из рисунка, после полного выведения антигенов из организма требуется большой промежуток времени до полного восстановления органа.
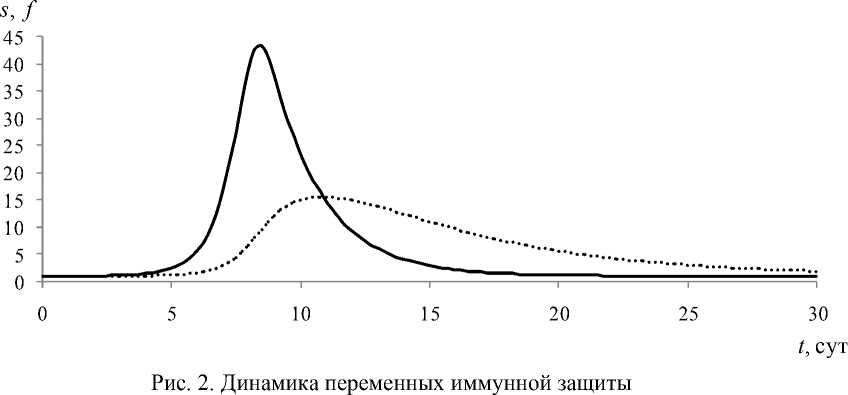
Динамика переменных иммунной защиты при острой форме изображена на рис. 2. Сплошной кривой показано изменение числа плазматических клеток, а пунктирной – концентрация антител. После нейтрализации антигенов еще достаточно продолжительное время наблюдается повышенная концентрация специфичных к данному антигену антител.
Алгоритм идентификации параметров управляемой модели
Среди приложений математических моделей иммунного ответа важное место занимает задача прогноза течения и исхода болезни для конкретного человека. Применения в клинической практике моделей иммунной защиты организма и подходы к построению управления иммунным ответом представлены в работе [7]. Методы статистического оценивания параметров моделей заболеваний по клиническим данным рассмотрены в работе [4].
Чтобы определить параметры модели при традиционных подходах, необходимо осуществить измерения фазовых переменных в течение всего периода протекания заболевания. Это означает, что полностью оценить параметры можно только к концу заболевания, когда прогноз его течения и исхода теряет свою актуальность. Поэтому необходима разработка таких алгоритмов идентификации параметров, которые бы позволяли осуществлять управление иммунным ответом параллельно с получением экспериментальных значений. Это позволит строить гибкие программы лечения на основе получаемых клинических данных.
Рассмотрим подход, при котором одновременно выполняется управление иммунным ответом и идентификация параметров модели. Будем использовать алгоритм дискретного управления иммунным ответом, предложенный в работах [8, 9]. Идея алгоритма заключается в том, что динамику какой-либо переменной инфекционного процесса необходимо вывести на желаемый режим, соответствующий в некотором смысле «идеальному» иммунному ответу.
Управляемая модель иммунного ответа при инфекционном заболевании может быть представлена в виде dx
— = F(a,x,u), x(0) = xo, t e [0, T], dt где a - вектор параметров модели, a e A c RL , L - количество параметров; x(t) -вектор фазовых переменных модели, x(t) e Rn, n - количество фазовых переменных; управляющая функция u = u(t), характеризующая скорость введения лекарственных препаратов, выбирается из множества
T
U = {u ( t ): u ( t ) = и — I e [0, B ], t e [ t i 4, t i ), t i = i A t , i = 1, N , A t = ^, t o = 0, u(T ) = U n _ , }. (9)
Ограничение B > 0 учитывает физиологически допустимые дозы применения препаратов. Параметры модели заданы на множестве
A = { a = ( a 1 , a 2 ,..., a L ): a - < a i < a * , i = 1, L}. (10)
Будем считать, что экспериментальные значения можно получить в узлах сетки
f T1
Л = tt, : t: = г A t , г = r , N , A t =— k (11)
iiN где r определяет промежуток времени от момента инфицирования до первого измерения. Соответственно, будем считать u0 = и1 =... = ur-1 = 0 .
В работе [5] показано, что максимум концентрации антигенов не зависит от дозы заражения, а определяется иммунологическим статусом организма по отношению к данному типу антигена. Поэтому начальную дозу заражения будем считать известной. Также известным будем считать промежуток времени от момента инфицирования до первого измерения.
Алгоритм заключается в следующем. Сначала определяется множество фазовых переменных y(t), по значениям которых будет проводиться идентификация (y(t) е Rm , m < n), и задаются величины допустимого отклонения расчетных значений от экспериментальных данных вj, j = 1, „., m. На множестве допустимых значений параметров A задается сетка дискретизации
0 = ^ а : a j
= а Г + Jhi , j = °- M i , h i =
i = 1, L f .
Затем случайным образом из узлов сетки (12) задается K наборов значений параметров:
а ( к ) е 0 , к = 1, K .
При t еЛ определяются допустимые наборы параметров, т.е. удовлетворяющие следующему критерию идентификации:
|у/ t , а ( к ) ) - y ;cn( t z )| < j i = r , N , к = 1, K z , j = 1, m , (14)
где K i - количество наборов параметров в момент t i .
Таким образом, после измерения значений фазовых переменных при t = t i необходимо найти K i решений задачи (8) на отрезке [0, t i ], i = r , .... N , и определить допустимые наборы параметров. В качестве оценки параметров при t = t i выбирается среднее значение допустимых наборов:
a i ) = к = 1
J i
I a jk )
J i
, j = 1, L , i = r , N ,
где J, - количество допустимых наборов значений параметров в момент времени t i ; J i < K i , i = r , ..., N ; K i = J i - 1 , i = r + 1, ., N ; Kr = K , где K - первоначальное количество наборов параметров; J i = K i - H i , i = r , ., N , где H i - количество неприемлемых наборов параметров в точке t i .
Обозначим y ( a ( i ) , ur , ..., u i , t i + 1) - прогноз значений фазовых переменных на следующий момент времени при данном управлении, где а ( 1 ) = { а( 1 ) , a( 1 ) , ..., a Li ) }, i = r , ..., N - 1.
В качестве переменной инфекционного процесса, которую необходимо вывести на желаемый режим, выбрана концентрация антигенов, так как с этой характеристикой связано протекание той или иной формы заболевания.
На основе подхода, предложенного в работе [8], определяются соответствующие «идеальному» иммунному ответу значения концентрации антигенов:
.x f ( a ( i ) , 0, ..., 0, t i + 1), i = r , N - 1. (16)
Если прогноз уровня концентрации антигенов на следующий момент времени x 1 ( a (‘) , ur , ..., u i - 1 , 0, t i + 1), i = r , ..., N- 1, не совпадает с «идеальным» значением, то в качестве управления подбирается такая величина u i , i = r , .., N - 1, которая обеспечивает переход фазовой траектории концентрации антигенов из точки x 1 эксп ( ti ) в точку x * ( a ( i ) , t i + 1), i = r , .... N - 1.
В качестве решения задачи идентификации параметров берется среднее значение допустимых наборов параметров в конце отрезка интегрирования:
JN la a ‘к’ _ ajN’ = , j = 1, L. (17)
J N
Таким образом, предложенный алгоритм позволяет построить управление в процессе идентификации параметров модели.
Результаты вычислительных экспериментов
Идентификация параметров модели проводилась по значениям, имитирующим клинико-лабораторные показатели. Для определения значений параметров были выбраны переменные инфекционного процесса: y ( t ) = { v ( t ), m ( t )} г . Множество значений { y эксп ( t ) = { v эксп ( t ), m эксп ( t )} r , t eQ } задавалось из решения задачи (6), (7) с интервалом времени A t = 1 сут. Интегрирование задачи (6), (7) проводилось на отрезке времени T = 14 сут.
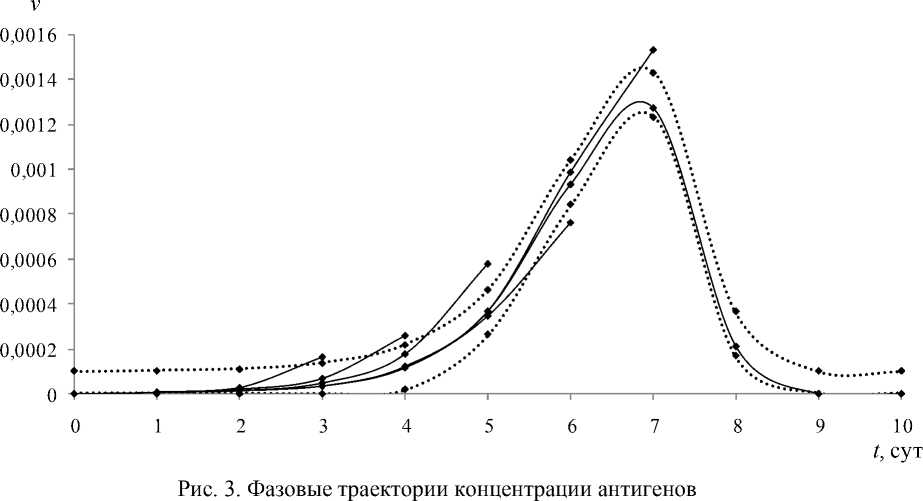
Различным значениям параметров модели соответствуют различные фазовые траектории. Идентификация параметров модели проводилась по значениям переменных инфекционного процесса, поэтому фазовые траектории выбранных характеристик должны лежать в некоторой окрестности экспериментальных значений. Таким образом, получаем область, в которой должны находиться фазовые траектории компонентов инфекционного процесса. На рис. 3 для функции v ( t ) границы этой области изображены пунктирными кривыми. Если при каком-либо наборе параметров траектория выходит за границы этой области в некоторой точке отрезка интегрирования, то дальнейшие вычисления с этим набором параметров не проводятся. На рис. 3 изображены возможные варианты выхода фазовых траекторий за границы допустимой области.
Рассмотрим управление иммунным ответом на примере иммунотерапии, которая заключается во введении готовых иммуноглобулинов или донорских антител. В рамках базовой математической модели инфекционного заболевания реализация иммунотерапии может быть отражена следующим образом [2]:
dv
= a l v - a 2 fv , dt
ds
— = aз^(m)f(t - t)v(t - t)9(t - t) - a5(5 -1), dt
df- = a4(5 - f) - a8 fv + u, dt dm
— = a 6 v
dt
- a 7 m .
На рис. 4 изображена реализация предложенного алгоритма. Считалось, что t r = 3 сут. После получения очередного экспериментального значения определяется прогноз уровня концентрации антигенов на следующий момент времени х /а( i ) , u r , ..., u i - 15 0, t i + 1), i = r , .„, N - 1. С помощью управления необходимо перевести фазовую траекторию в «идеальную» точку. Как видно из рисунка, фазовая траектория, построенная на основе имитации экспериментальных значений, проходит вблизи «идеальных» точек.
v
0,0006
0,0005
0,0004
0,0003
0,0002
0,0001
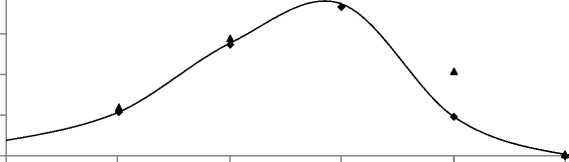
Рис. 4. Реализация алгоритма: ♦ – «идеальные» значения; — – реальная траектория;
▲ – прогноз на следующий момент без управления
■*--------------*
t , сут
Результаты идентификации параметров при K = 104 представлены в табл. 1. Средняя погрешность оценки параметров составляет 8,06%.
Вид управляющей функции представлен на рис. 5. Сплошными линиями показаны результаты построения управления при параллельной идентификации параметров, а штриховыми – управляющая функция, построенная с заданным набором значений параметров. Из рисунка видно, что управление в условиях неполной информации лишь незначительно (до 10%) отличается от «идеального» управления.
В табл. 2 показаны средние значения допустимых наборов параметров в узлах сетки (11). Таким образом, можно сделать вывод о том, что предложенный алгоритм, учитывающий среднее значение допустимых наборов параметров в данный момент времени, позволяет достаточно точно оценить параметры модели и построить управление (программу лечения), близкое к «идеальному».
Таблица 1
Результаты идентификации параметров
|
Параметр |
a 1 |
a 2 |
a 3 |
a 4 |
a 5 |
a 6 |
a 7 |
a 8 |
|
Нижняя граница |
1,75 |
0,55 |
9550 |
0,145 |
0,25 |
7,5 |
0,095 |
5,5 |
|
Верхняя граница |
2,25 |
1,05 |
10 550 |
0,195 |
0,75 |
12,5 |
0,145 |
10,5 |
|
Шаг |
0,1 |
0,1 |
100 |
0,01 |
0,1 |
1 |
0,01 |
1 |
|
Оценка |
2,150 |
0,650 |
10 050 |
0,175 |
0,375 |
10,000 |
0,112 |
8,250 |
|
Погрешность, % |
7,50 |
18,75 |
0,50 |
2,94 |
25,00 |
0,00 |
6,67 |
3,13 |
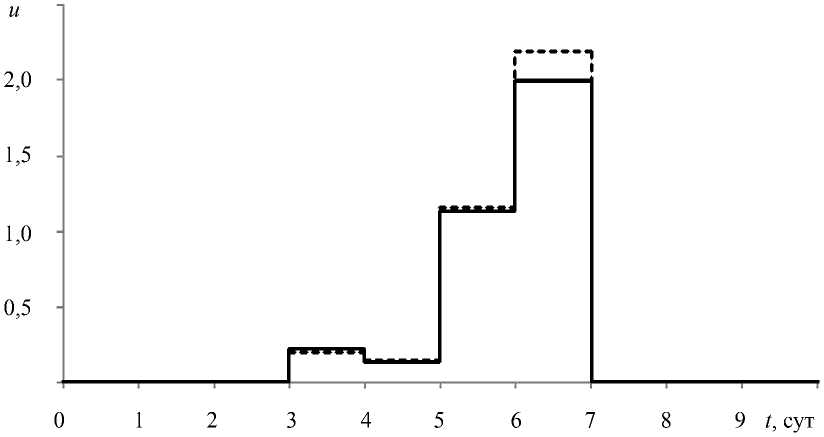
Рис. 5. Вид управляющей функции
Таблица 2
|
ti |
Ki |
Hi |
a 1 |
a 2 |
a 3 |
a 4 |
a 5 |
a 6 |
a 7 |
a 8 |
|
3 |
10 000 |
297 |
2,000 |
0,802 |
10047 |
0,170 |
0,503 |
10,010 |
0,120 |
8,006 |
|
4 |
9703 |
2716 |
2,000 |
0,804 |
10047 |
0,170 |
0,502 |
10,018 |
0,120 |
8,008 |
|
5 |
6987 |
5575 |
1,993 |
0,805 |
10053 |
0,170 |
0,505 |
9,962 |
0,121 |
8,008 |
|
6 |
1412 |
1223 |
1,983 |
0,796 |
10066 |
0,170 |
0,493 |
9,897 |
0,121 |
8,093 |
|
7 |
189 |
105 |
2,007 |
0,790 |
10088 |
0,170 |
0,493 |
9,488 |
0,121 |
8,286 |
|
8 |
84 |
41 |
2,017 |
0,799 |
10115 |
0,172 |
0,487 |
9,616 |
0,118 |
8,151 |
|
9 |
43 |
16 |
2,061 |
0,794 |
10085 |
0,168 |
0,472 |
9,833 |
0,114 |
8,093 |
|
10 |
27 |
8 |
2,087 |
0,808 |
10050 |
0,167 |
0,497 |
10,132 |
0,112 |
8,237 |
|
11 |
19 |
5 |
2,114 |
0,800 |
10014 |
0,168 |
0,479 |
10,143 |
0,114 |
8,000 |
|
12 |
14 |
4 |
2,120 |
0,770 |
9920 |
0,165 |
0,480 |
10,400 |
0,113 |
8,100 |
|
13 |
10 |
3 |
2,093 |
0,707 |
9979 |
0,172 |
0,421 |
10,643 |
0,109 |
8,214 |
|
14 |
7 |
3 |
2,150 |
0,650 |
10050 |
0,175 |
0,375 |
10,000 |
0,112 |
8,250 |
Последовательность оценки параметров
Заключение
Из анализа представленных результатов можно сделать вывод о том, что предложенный алгоритм позволяет достаточно точно оценить параметры модели при относительно небольших вычислительных затратах, а также построить программу лечения в процессе идентификации параметров. Таким образом, данную методику можно применять для идентификации конкретных моделей иммунного ответа при инфекционных заболеваниях по имеющимся клиническим данным. Рассмотренный алгоритм также может быть использован для идентификации других моделей, описанных динамическими системами, при этом необходимо, чтобы были информативны фазовые переменные, по которым проводится идентификация.
Список литературы Идентификация параметров и управление в математических моделях иммунного ответа
- Белых Л.Н. Анализ математических моделей в иммунологии.-М.: Наука, 1988. -192 с.
- Болодурина И.П., Луговскова Ю.П. Оптимальное управление иммунологическими реакциями организма человека//Проблемы управления. -2009. -№ 5.-С. 44-52.
- Дасгупт Д. Искусственные иммунные системы и их применение. -М.: Физматлит, 2006. -343 с.
- Зуев С.М. Статистическое оценивание параметров математических моделей заболеваний. -М.: Наука, 1988. -172 с.
- Марчук Г.И. Математические модели в иммунологии. -М.: Наука, 1980. -264 с.
- Марчук Г.И. Математические модели в иммунологии. Вычислительные методы и эксперименты. -М.: Наука, 1991. -304 с.
- Погожев И.Б. Применение математических моделей заболеваний в клинической практике. -М.: Наука, 1988. -190 с.
- Русаков С.В., Чирков М.В. Дискретное управление в простейшей математической модели инфекционного заболевания//Вестник Перм. ун-та. Математика. Механика. Информатика. -2011. -Вып. 4 (8). -С. 59-63.
- Русаков С.В., Чирков М.В. Математическая модель влияния иммунотерапии на динамику иммунного ответа//Проблемы управления. -2012. -№ 6. -С. 45-50.


