Идентификация параметров повреждений в упругом стержне с использованием конечно-элементного и экспериментального анализа мод изгибных колебаний

Введение. Известная классификация задач идентификации параметров повреждений включает в себя четыре уровня достигаемых целей [1, 2]. Решение задач первого уровня заключается в обнаружении повреждений. Ко второму уровню относятся задачи локации повреждений в стержнях и конструкциях. Третий уровень включает в себя как обнаружение повреждений и расчет его местоположения, так и оценку степени опасности этих повреждений. И, наконец, наиболее сложные цели достигаются в процессе решения задач четвертого уровня, связанных с прогнозированием остаточного ресурса конструкции в целом.

Большинство известных работ по идентификации повреждений посвящены решению задач 1-го и 2-го уровня [2-10]. Значительная часть из них включает в себя результаты исследований параметров колебаний стержней и балок и в меньшей степени – более сложных структур, состоящих из связанных элементов конструкций с открытыми трещинами. В недавнем обзоре работ по идентификации повреждений в конструкциях проанализированы результаты решения задач всех четырех уровней [11], а также рассмотрены различные алгоритмы решения задач идентификации. Постановка этих задач использует влияние параметров повреждений на изменение собственных частот и форм колебаний, кривизны этих форм, расчет матриц податливости и демпфирования дефектных структур.

Исследования изменений собственных частот колебаний, обусловленных глубиной закрывающейся трещины, выполнены в работах В.В. Матвеева и А.П. Бовсуновского [4-6]. К сожалению, результаты конечно-элементного анализа, проведенного в этих работах, не были полностью подтверждены натурным экспериментом. В работе [7] приведены результаты конечноэлементных исследований параметров повреждений в стержнях, основанные на анализе суб- и супергармонических резонансов. Однако измерения характеристик колебаний дефектного стержня, проведенные экспериментально, не вполне подтвердили выводы, сделанные из численного эксперимента. Поэтому предложенный в [7] диагностический признак повреждений требует дальнейших исследований.

В работах Mohammad M.F. Dado, Omar A. Shpli, Y.Bamnios и др. [2,3] использовалась конечно-элементная модель стержня с аналогом повреждения в виде дискретного упругого элемента. Его податливость вычислялась A.D. Dimaragonas и др. [8], а позже Dado и Shpli [2] через локальную податливость трещины C ij , выражающуюся в виде интеграла, зависящего от глубины трещины и факторов интенсивности напряжений в окрестности трещины на I, II и III модах колебаний. Однако сложность предварительного анализа напряженно-деформированного состояния материала вблизи трещины значительно снижает преимущества использованного метода идентификации.

В связи с изложенным представляется перспективным исследовать не только изменение собственных частот колебаний дефектной стержневой конструкции, но и соответствующих собственных форм, т.е. распределения амплитуд колебаний по длине стержня с трещиной [12, 13]. Учитывая также расширенные возможности современных конечно-элементных (КЭ) пакетов, исследование целесообразно провести без выполнения отдельного анализа напряженно-деформированного состояния материала вблизи трещины. Такой подход должен дать более полную информацию о закономерностях влияния параметров повреждения на характеристики колебаний дефектной конструкции, тем самым позволив сформулировать и экспериментально проверить некий комплексный признак наличия, локализации и степени поврежденности.

Цель настоящего исследования – поиск и обоснование диагностического признака, характеризующего местоположение повреждения и степень поврежденности консольно закрепленного упругого стержня с помощью конечно-элементного моделирования и натурного эксперимента на основе анализа особенностей на графиках форм нескольких первых мод колебаний.

Конечно-элементное моделирование стержня с разрезом. С помощью конечноэлементного комплекса ANSYS была построена полнотелая модель на основе 3D элемента solid92. Разбивка моделей на узлы по длине производилась кратной 1/40 от общей длины балки. Количество конечных элементов – более 5000. Повреждение моделировалось надрезом шириной 1 мм. Сетка имела двукратное сгущение в месте расположения дефекта.

При различном местоположении повреждения в результате модального анализа были получены собственные частоты и соответствующие формы колебаний.

На 1-й, 2-й и 3-й модах изгибных колебаний консольно закрепленного стержня с надрезом регистрировалось распределение амплитуд поперечных смещений по длине стержня L 0 с интервалом 0.1 L , где L = L_i / L ₀ , ( L_i - расстояние от дефекта до ближайшего конца стержня). Вычисления производились при относительной глубине надреза t = t_i / a ( t_i - абсолютное значение глубины надреза, а- высота поперечного сечения стержня), принимающей значения t =0,3; 0,5; 0,7; 0,86 и для неповрежденного t =0 (рис.1).

Рассматривалась гипотеза о том, что изломы на графиках форм колебаний позволяют локализовать повреждение в стержне. Для проверки ее обоснованности был выполнен анализ графиков этих форм колебаний, который показал следующее. На графиках форм колебаний 1-й и 3-й мод колебаний (рис.1, а, д ) обнаружены изломы при расположении надреза L_с =0,25 глубиной t =0,3; 0,5; 0,7 и 0,86, отсутствовавшие на графиках форм колебаний неповрежденного стержня.

На форме 2-й моды колебаний (см. рис.1, в ) незначительный излом графика наблюдается только при глубине надреза t =0,86. Угол этого излома (между касательными к графику кривой с обеих сторон от излома) составляет около ϕ =175⁰ (см. рис.1, в ). Для графиков 1-й и 3-й мод этот угол существенно меньше (см. рис.1, а , д ). Эти результаты отличаются от ранее опубликованных [9] авторами в той части, что на графиках 2-й моды колебаний стержня (см. рис.1, в ) проявляется особенность, кореллирующая с местоположением и глубиной надреза (повреждения), хотя и в слабой степени. В работе [9] эта особенность не была обнаружена.

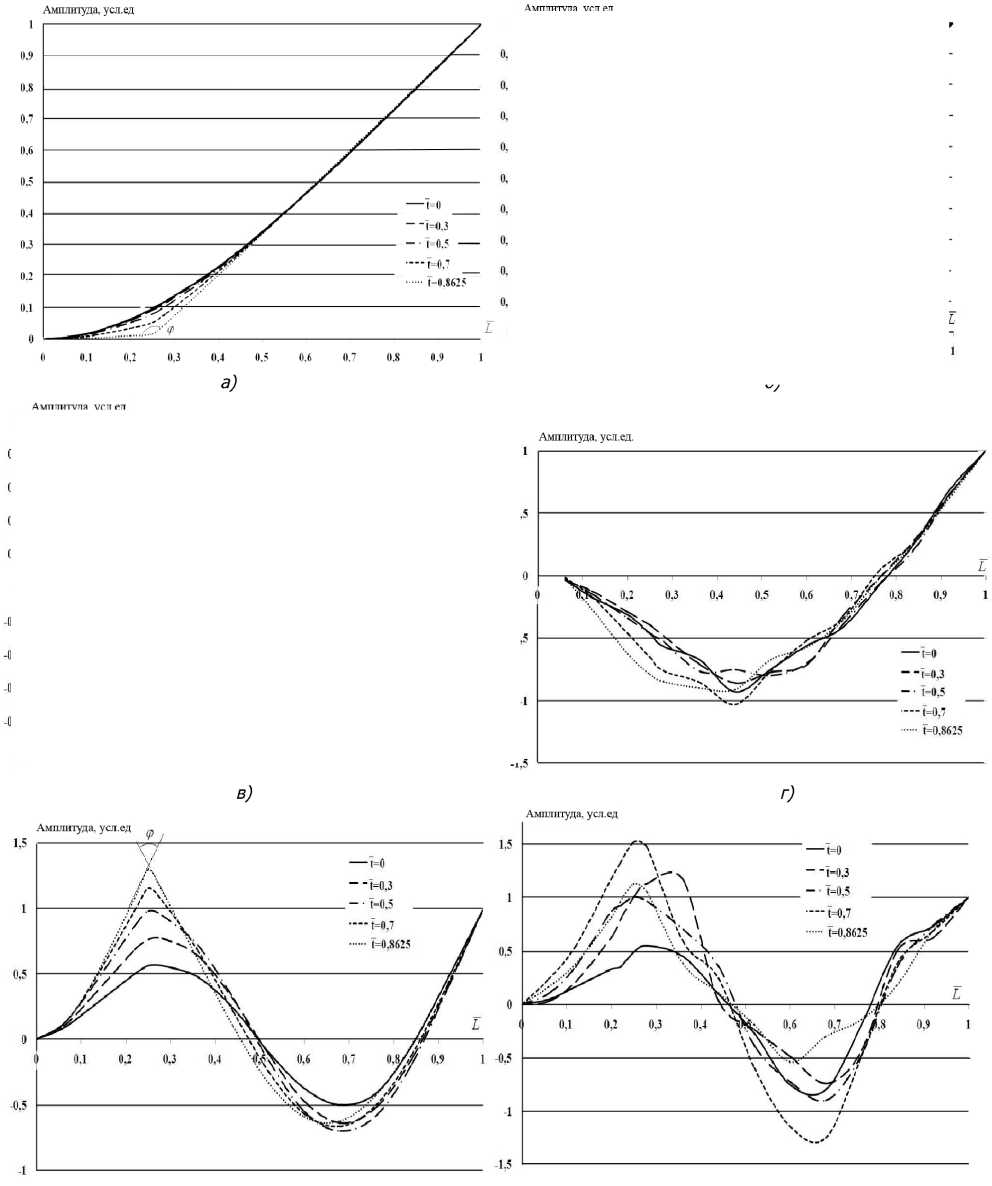
д)

е)

Рис.1. Формы 1-й ( а , б ), 2-й ( в , г ) и 3-й ( д , е ) мод поперечных колебаний стержня с повреждением в виде надреза на расстоянии L_с =0,25 от защемления при различной степени поврежденности t , рассчитанные в КЭ-комплексе ANSYS ( а , в , д ) и полученные экспериментально ( б , г , е )

Для выявления причин расхождения результатов КЭ анализа на втором этапе работы были проведены экспериментальные исследования форм колебаний кантилевера с надрезом.

При этом геометрические и массовые характеристики испытуемых образцов не отличались от использованных в конечно-элементной модели.

Натурный эксперимент. Экспериментальные исследования были проведены на специально разработанном информационно-измерительном комплексе ИИК-210; его структурная схема и общий вид показаны на рис.2. Образец 1 - металлический стержень из стали 3 размером 4х8х250 мм консольно закреплен в опоре-держателе 2, установленной на основании 3. Вынужденные изгибные колебания образца создаются с помощью электромагнитного возбудителя 4 модели ЭМВ210, который питается переменным током от усилителя мощности 5 модели LV102 . Частота колебаний регулируется генератором 6 Г6-27, а амплитуда – изменением коэффициента усиления усилителя 5. Формирование возбуждающего сигнала возможно также с использованием виртуального генератора на базе модуля цифроаналогового преобразования (ЦАП) 7 модели Е-14-440 фирмы L-Card .

Регистрация частоты изгибных колебаний образца производится частотомером Ч3-33 (8), а форма колебаний возбуждающего напряжения - цифровым осциллографом LeCroy WS-422 (9). Вертикальные и боковые смещения точек поверхности образца при изгибных колебаниях регистрировались с помощью пары оптических датчиков РФ 603 10 и 11, которые могли перемещаться вдоль образца без изменения базового расстояния между его плоскостью и рабочей поверхностью датчиков. Виброускорения регистрировались вибродатчиком 12 модели ADXL-203. Управление модулем АЦП/ЦАП (7, 13) и обработка регистрируемого сигнала осуществлялись с помощью оригинальной программы ИИК-210.

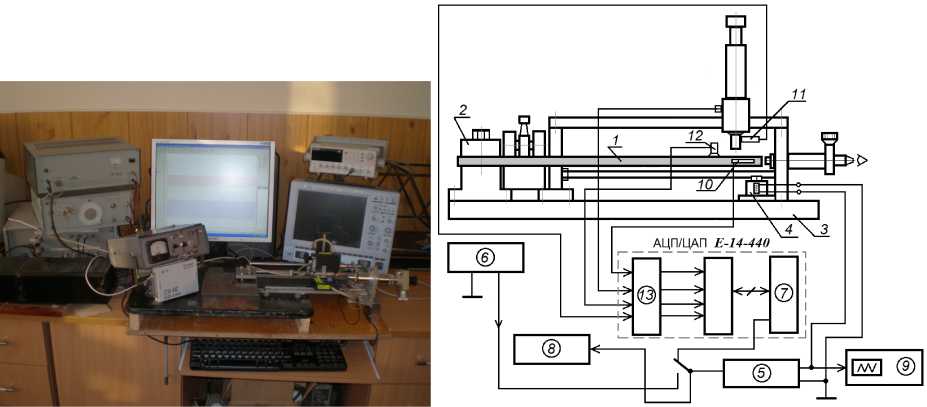
Рис.2. Общий вид и структурная схема комплекса ИИК-210

Снятие амплитудно-частотных характеристик производилось в диапазоне частот 0…2000 Гц. Последовательно на 1-й, 2-й и 3-й модах колебаний регистрировались распределения амплитуд вертикальных смещений по длине образца с помощью перемещаемых оптических датчиков. По полученным данным восстанавливались формы колебаний всех трех исследуемых мод колебаний. Описанный алгоритм эксперимента был применен к неповрежденному образцу ( t =0) и к образцам с увеличивающейся глубиной надреза t =0,3; 0,5; 0,7; 0,86, расположенного на расстоянии L_с =0,25 от заделки (см. рис.1, б , г , е ).

Сравнительный анализ форм колебаний, полученных методом конечных элементов (см. рис.1, а , в , д ) и в эксперименте (рис.1, б , г , е ) показал изломы и перегибы на формах 1-й и 3-й мод колебаний на расстояния L_с =0,25-0,27 от заделки для всех надрезов глубиной t =0.3; 0.5; 0.7; 0.86. На графиках, полученных методом конечных элементов (см. рис.1, а, д ), в зоне распо- 315

ложения дефекта наблюдаются изломы; на экспериментальных кривых (см. рис.1, б, е ) эти изломы значительно сглажены. Их координаты определены нами по точкам пересечения касательных к прилагающим с обеих сторон участкам кривой до и после перегиба. При этом угол ϕ между этими касательными уменьшается с ростом глубины надреза, что вполне объяснимо уменьшением жесткости стержня с увеличением глубины надреза. На формах 1-й и 3-й мод колебаний для образцов без надреза изломы отсутствуют.

Характер изменения формы колебаний на 2-й моде (см. рис.1, в, г ) при появлении разреза отличается от закономерностей, выявленных на 1-й и 3-й модах. Численным экспериментом выявлена очень слабая особенность в поведении 2-й моды колебаний (см. рис.1, в ) и только при максимальной глубине надреза t =0,86. На экспериментальных кривых для координаты надреза L _с =0.25 (см. рис.1, г ) надежно регистрируются резкие изменения поведения форм колебаний уже начиная с t =0,7. Этот результат выявляет некоторую ограниченность метода конечных элементов (во всяком случае, в использованной постановке задачи) для построения модели диагностирования параметров повреждения. Совместное использование обладающего высокой чувствительностью физического эксперимента с анализом форм колебаний на собственных частотах и метода конечных элементов, позволяющего выявить ясную картину полуколиче-ственных закономерностей модификации собственных форм, по-видимому, является перспективным методом диагностирования дефектов типа трещин при возбуждении изгибных колебаний в балочных конструкциях.

Выводы. Анализ форм 1-й и 2-й мод изгибных колебаний стержней с дефектом типа трещин колебаний выявил особенность этих форм в виде изломов, координаты которых совпадают с местоположением повреждения (надреза). Угол между касательными к графику формы колебаний, проведенными при переходе через координату повреждения, непрерывно уменьшается с ростом глубины надреза, тем самым характеризуя степень поврежденности. Оба этих параметра в совокупности могут служить диагностическим признаком, характеризующим место и степень поврежденности консольно закрепленного упругого стержня с высокой степенью достоверности. Количественные расчеты углов между касательными к кривым форм колебаний будут получены позже в рамках дальнейших исследований.

Заключение. Предложен комбинированный конечно-элементный и экспериментальный метод идентификации параметров повреждений в стержневых конструкциях, позволяющий с высокой достоверностью оценить местоположение и степень поврежденности.

Работа выполнена при поддержке РФФИ (грант №10-08-00093а, 10-08-05011-б, 10-08-13300-РТ_ОМИ).