Идентификация статистической зависимости времени кругового обращения пакетов от загрузки сетевого соединения

воздействия большого числа неконтролируемых факторов динамика RTT не может быть описана сколько-нибудь реалистичной детерминированной закономерностью. Поэтому разработка и апробация статистических моделей для времени кругового обращения пакетов остается актуальной проблемой теории и практики сетей передачи данных.

Развитие идей, связанных с синтезом и применением стохастических моделей RTT, можно проследить по публикациям [1–7]. В [1, 2] получены результаты по временному и пространственному изменению RTT, причем в [1] предложено использовать для RTT семейство гамма-распределений. В [3] описана структура телекоммуникационной сети, которая порождает смесь гамма-распределений в качестве модели времени выполнения запроса. В [4] указано на наличие тяжелых хвостов, свойственных распределениям Парето. Распределение со степенными хвостами получено в [5] как эргодическое распределение, соответствующее динамической модели RTT в виде некоторого нелинейного стохастического дифференциального уравнения. Статистические модели RTT использованы в [6, 7] для синтеза стратегий управления загрузкой и фильтрации ненаблюдаемого состояния сетевого соединения.

Для оценки RTT на сегодняшний день сформировались два подхода, основанных на активных [8] и, соответственнo, пассивных методах [9, 10]. Активные методы включают в себя воздействие на состояние сетевого соединения путем организации дополнительного трафика, например, отправка пробных пакетов или сервисных сообщений. Пассивные методы используют данные, формирующиеся при обычной работе телекоммуникационных устройств с помощью штатных средств сбора данных.

В данной статье рассматривается активный мониторинг состояния беспроводного соединения с помощью пробных пакетов в рамках протокола ICMP (Internet Control Message Protocol). Использование ICMP-пакетов имеет несколько преимуществ, поскольку позволяет избежать высокой дополнительной нагрузки, порождаемой пробными пакетами, и не требует привилегированного доступа, который требуется для получения статистики с узлов сети. Кроме того, для организации мониторинга можно воспользоваться хорошо известными утилитами, такими как ping , реализованными на платформах Windows и UNIX. Моделирование «полезной» загрузки соединения производилось с помощью D-ITG генератора трафика [11], который позволяет организовать стационарный поток TCP-пакетов с заданным распределением времени между отправками пакетов.

Цель проведения указанного эксперимента состояла в выяснении статистической зависимости времени кругового обращения пакетов от уровня загрузки сетевого соединения. Более аккуратно эту проблему можно сформулировать как задачу определения условного распределения Law(R | т ) , где R — это RTT для ICMP-сообщений, а т — время между отправками TCP-пакетов. Однако прежде решения данной проблемы необходимо проанализировать статистическую воспроизводимость самого эксперимента. Положительный вывод об этом можно сделать на основании совпадения оценок распределения RTT, вычисленных двумя способами:

• 1)    нахождение эмпирического распределения R в эксперименте, где величина т моделируется с равномерным распределением на некотором промежутке [т _а ,т ь ] ;

• 2)    определение Law(R) по формуле полной вероятности, в которой Law(R | т = т - ) , j = 1,...,m , суть эмпирические распределения из соответствующих m экспериментов с учетом того, что значения { т - } образуют равномерную сетку на [ т _а ,т ь ] , а вероятности Р { т = т - } одинаковы.

• 2.    Модель

После подтверждения устойчивости статистической зависимости RTT от загрузки сети для эмпирических плотностей RTT было найдено приближение в виде смеси обобщенного распределения экстремальных значений и логистического распределения. Оценки параметров распределений получены методом максимального правдоподобия, а веса в смеси оценены с помощью EM-алгоритма.

Рассмотрим систему массового обслуживания (СМО), имеющую два входа (потоки № 1 и № 2) и два выхода. Заявки из обоих входов выбираются в соответствии с некоторой дисциплиной и для каждого входа имеется собственная очередь. Данная СМО моделирует Wi-Fi соединение между двумя компьютерами. На ее входы поступают потоки заявок, которые соответствуют потокам TCP и ICMP-пакетов соответственно.

Пусть t j —моменты прихода заявок на вход № 1, тогда интервал времени между последовательными приходами заявок на вход № 1 обозначим как

^T j = ^t j    ^t j - i ,  ³ >  ¹

Для потока № 2 введем следующие обозначения: Т і — момент прихода г -й заявки из потока №2, а Т і — момент окончания обработки г -й заявки из потока № 2. Время кругового обращения ICMP-пакета соответствует времени полного обслуживания в СМО. Обозначим его R i , тогда для г -й заявки второго потока оно равно

R i = Т і

- Т і .

Коэффициент загрузки СМО

Ai(t) + A2(t)

*) =     ,(t)    '

где A i , A 2 — интенсивности поступления заявок для потоков №№ 1 и 2 соответственно, а ц есть интенсивность обработки заявок в системе.

Если поток пробных заявок обладает сравнительно малой интенсивностью по сравнению с основным потоком, т.е. выполняется

^A 2 <  ^A 1 '

то коэффициент загрузки преимущественно определяется потоком № 1:

p ^{( t}

^A 1 ^{( t )} p ^{( t )} .

TCP-пакетов общим размером 64 КБ. Выбор такого размера обусловлен технической сложностью точного поддержания заданного распределения т (точность ограничена таймером предоставляемым операционной системой) при больших нагрузках на соединение. Так как указанный размер превышает MSS = 1460 байт (при MTU = 1514 байт), каждый раз передается 45 последовательных пакетов с небольшой задержкой между ними. При этом ITGRecv передает в обратную сторону подтверждения на каждый полученный TCP-пакет. Для краткости далее под отправкой TCP-пакета имеется в виду отправка серии пакетов суммарного размера 64 КБ.

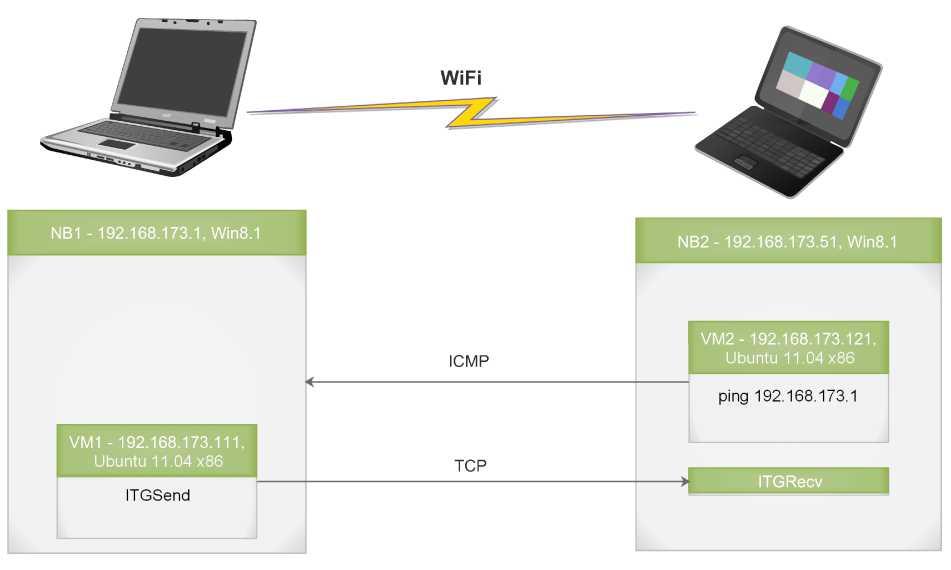
Рис. 1. Схема эксперимента

Внутри ВМ2 запущена утилита ping для отправки ICMP эхо-запросов в направлении NB1. Время между последовательно отправленными пакетами составляет 1 секунду, а размер каждого пакета 64 байта. При запуске утилиты ping используются следующие параметры:

ping -i 1 -W 1 -c 3600 192.168.173.1 .

Максимальная пропускная способность Wi-Fi соединения в эксперименте составляла C max = 65 Мбит / с (802.11n). Расстояние между NB1 и NB2 составляло 65 см.

• 4.    Результаты экспериментов

• 4.1.    Серия экспериментов с постоянным временем между TCP-пакетами

Описанная выше экспериментальная установка позволяет получать распределения R для различных распределений т . Ниже описаны две серии экспериментов с двумя различными распределениями: детерминированным и равномерным.

Пусть время между последовательными отправками серий TCP-пакетов является детерминированным. Серия таких экспериментов с различными значениями интенсивности отправки пакетов позволяет получить оценку закона условного распределения Law ( R i | т) .

С учетом пропускной способности C max и размера нагрузки 64 КБ был определен ряд т = Т ^ , к = 0,10 , которые бы соответствовали коэффициентам загрузки сети р от 0 до 1.

Для каждого из этих значений были получены замеры RTT R i за временной промежуток в 1 час.

В табл. 1 представлены значения т к , полученные выборочные средние, медианы, моды и среднеквадратичные отклонения RTT R . По данным из табл. 1 легко видеть, что при увеличении т возрастает как выборочное среднее, так и медиана R . При этом мода ведет себя иначе: она почти постоянна при т Е [15.38; 76.92] мс, но затем значительно изменяется при т <  12.82 мс.

Гистограммы RTT для всех экспериментов приведены на рис. 2 и 3. По ним видно, что хвост гистограммы постепенно увеличивается, но мода долгое время сохраняется постоянной вплоть до т = 12.82 мс.

Таблица1

Выборочные средние, медианы, моды и среднеквадратичные отклонения R для различных т

		т к , мс	R k , мс	median R k , мс	mode R k , мс	S R k , мс
		∞	2.6391	1.9720	1.9720	6.1714
		76.92	3.5788	1.7300	1.5700	6.5146
		38.46	3.6481	2.0000	1.5700	3.4934
		25.64	4.2819	2.6900	1.5500	13.3453
		19.23	5.1001	3.7900	1.4900	3.9964
		15.38	6.2625	5.6000	1.5100	4.8636
		12.82	9.3131	7.6600	10.0000	7.7647
		10.98	13.1969	11.9000	17.3000	7.0816
		9.615	25.1624	24.9000	26.5000	8.0855
		8.547	23.8942	23.6000	21.9000	6.9308
		7.692	24.3593	23.8000	23.9000	9.9954
„0.2 ЕОЛ °( го 0 2 Зол s0.2 Зол „0.2 > °( «0.2 ^ол
			1                                                                                           1                                                                                           1                                                                                          1                                                                                           1                                                                                           1                                                                                           1 —                  1                          1                          1                         1                          1                          1                          1
	5           10		15         20         25         30         35         40         45         50
			I                                                                                           I                                                                                           I                                                                                          I                                                                                           I                                                                                                                                                                                        I —                  I______________________________I______________________________I______________________________I______________________________I______________________________I______________________________I______________________________
	5           10		15         20         25         30         35         40         45         50
			I                                                                                           I                                                                                           I                                                                                          I                                                                                           I                                                                                           I                                                                                           I —                             I                                    I                                    I                                    I                                    I                                    I                                    I
	5           10		15         20         25         30         35         40         45         50
				1                                                                                           1                                                                                          1                                                                                           1                                                                                           1                                                                                           1 1                                                                                           1                                                                                          1                                                                                           1                                                                                           1                                                                                           1
	5          10          15			20         25         30         35         40         45         50
	1                                                            1		I                                                                                           I                                                                                           I                                                                                          I                                                                                           I                                                                                           I                                                                                           I ■■■—----L-             L              I               I               I               I               I
"о            5           10			15         20         25         30         35         40         45         50 R, ms

Рис. 2. Гистограммы R в серии экспериментов при т Е [15; 76] мс

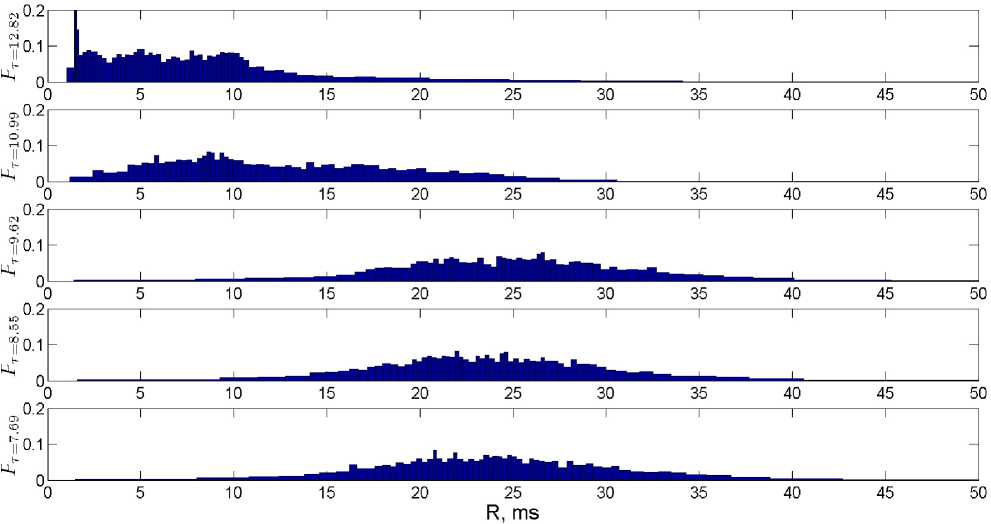
Рис. 3. Гистограммы R в серии экспериментов при т е [7; 13] мс

• 4.2.    Эксперимент с равномерно распределенным временем между TCP-пакетами

Обозначим т у случайную величину, равномерно распределенную на заданном отрезке [ т _а ; т ь ] . Пусть время т между заявками в потоке № 1 подчиняется указанному распределению. То есть TCP-пакеты отправляются через псевдослучайные интервалы времени, которые распределены равномерно. В результате двух таких экспериментов длительностью 8 часов каждый были получены оценки распределения RTT R при равномерно распределенных т = т у , т.е. La'w ( R\т у ) . В одном случае т _а = т 8 = 9.62 , т ь = т = 76.92 , а в другом - т _а = т = 8.54 , т ь = т 5 = 15.38 .

Обозначим / r ( t | т у ) плотность распределения Law(R | т у ) . Тогда в соответствии с формулой полной вероятности должно быть верно следующее выражение:

m

J r ⁽ ж | ^т у ) = / s ⁽ ж | ^т = т) = ^ / д ⁽ ж | ^т = т ^{) р} \ т _г ^е A j ^} ,                ⁽⁶⁾

3=1

где т - набор базовых значений т из серии экспериментов, описанной в разделе 4 (значения приведены в табл. 1), а A j есть последовательность полуинтервалов следующего вида:

^А з =[2 ^{( т} 3 ^{+ т} з - 1 ); 2 ^т + ^т 3+1 ⁾) , 3> 0.                     ⁽⁷⁾

Формула (6) позволяет проверить статистическую воспроизводимость эксперимента. Для проверки были использованы ядерные оценки плотностей, построенные на основе выборок, сравнение левой и правой частей (6) показаны на рис. 4, 5.

• 5.    Анализ результатов

  • 5.1.    Выбор распределений

Распределения RTT оценивались разнообразными способами и разными распределениями: сдвинутым гамма-распределением [1], Парето-распределением [4].

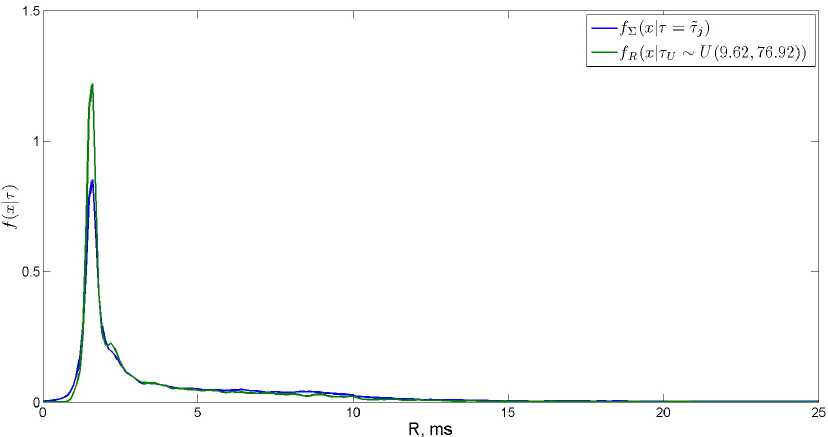
Рис. 4. Ядерные оценки плотностей / д ( ж | т у ) и / в ( ж | т = т , ) при т _а = 9 . 62 , т ь = 76 . 92

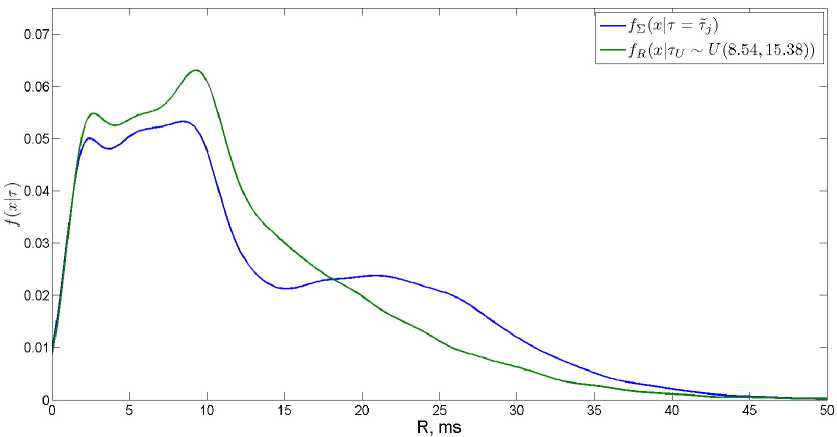
Рис. 5. Ядерные оценки плотностей / д ( ж | т у ) и / в ( ж | т = T j ) при т _а = 8 . 54 , т ь = 15 . 38

Результаты при малых нагрузках соединения действительно похожи на [4, 9]. Однако по мере уменьшения т эмпирическая оценка плотности распределения сильно меняется и становится более похожей на смесь распределений.

Из рис. 2 и 3 видно, что min R >  0 , т.е. RTT имеет положительное минимальное значение. RTT по определению – положительная величина и всегда выше некоторого порогового значения, поэтому распределение R должно быть сдвинутым на некоторую пороговую величину.

Обозначим пороговый параметр 0 . В качестве оценки этого параметра будем использовать

0 = 0.99 min R.                                    (8)

Применяя эту оценку, получим несдвинутую выборку RTT R :

R = R - 0,                                    (9)

которую и будем использовать для оценки параметров несдивнутых распределений.

Результаты для больших т можно приблизить семейством обобщенных распределений экстремальных значений (generalized extreme-value, GEV) либо Парето-распределением.

На рис. 6 представлено сравнение гистограммы для выборки R и плотностей GEV и Парето-распределений при т = 38.46 . Оценки параметров получены с помощью метода максимального правдоподобия. Из результатов видно, что наиболее подходящим является GEV-распределение, плотность которого имеет вид [12]:

л 1 (—^  1)-1)     г- - « V1—1„

ЛОг^/л,^ = —eV           V 1 + £----- .

У1^

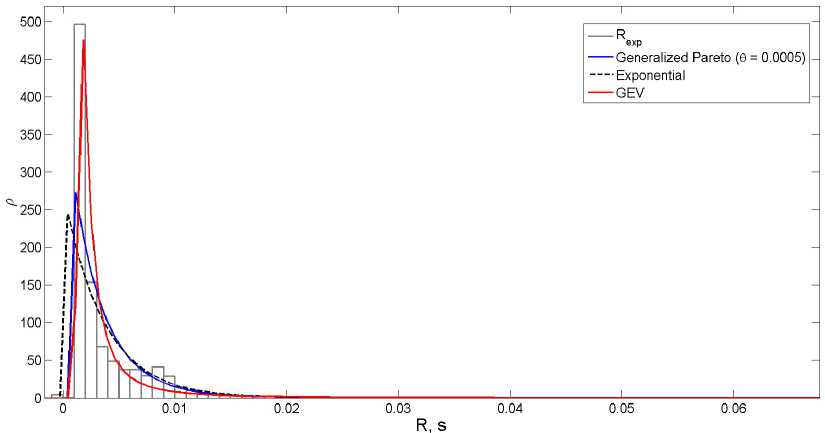
Рис. 6. Гистограмма и оценки плотностей для т = 38 . 46

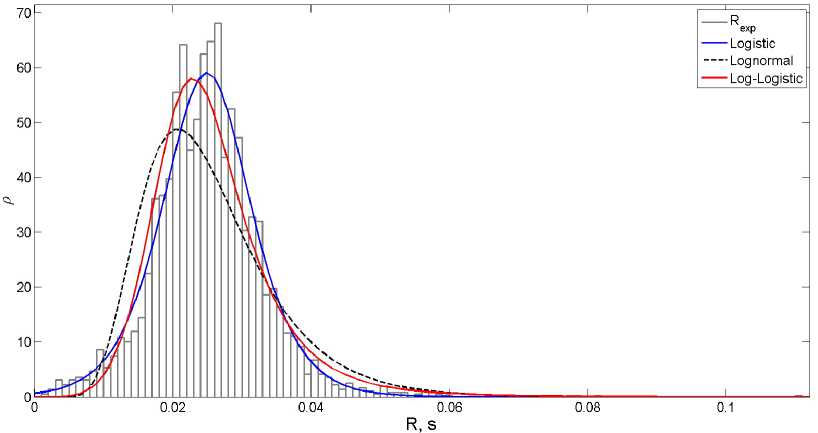
Рис. 7. Гистограмма и оценки плотностей для т = 9 . 615

При малых т наиболее подходящей оценкой является логистическое распределение

/ 2 ⁽ Ж | // 2 ,СТ 2 ⁾ =

"~М 2

e ^ст 2

"-М2   2 , ст2 11 + e ст2   I

т.к. его плотность имеет более тяжелый хвост и больший коэффициент эксцесса, чем нормальное распределение. На рис. 7 представлено сравнение гистограммы для выборки R, полученной при т = 9.615, и плотностей нескольких распределений c параметрами, полученными методом максимального правдоподобия.

Промежуточные случаи можно приблизить смесью указанных распределений. В следующем разделе описан алгоритм разделения смеси распределений и приведены результаты разделения.

• 5.2.    Разделение смеси распределений

Предположим, что плотность распределения RTT представима в виде выпуклой комбинации обобщенного распределения экстремальных значений f i и логистического распределения / 2 , то есть имеет место

/ д (ж | т = т) = W 1 ( T ) f 1 ( x - Ө) + W 2 ( T ) f 2 ( x - Ө ) ,                     (12)

где w 1 + w ₂ = 1 .

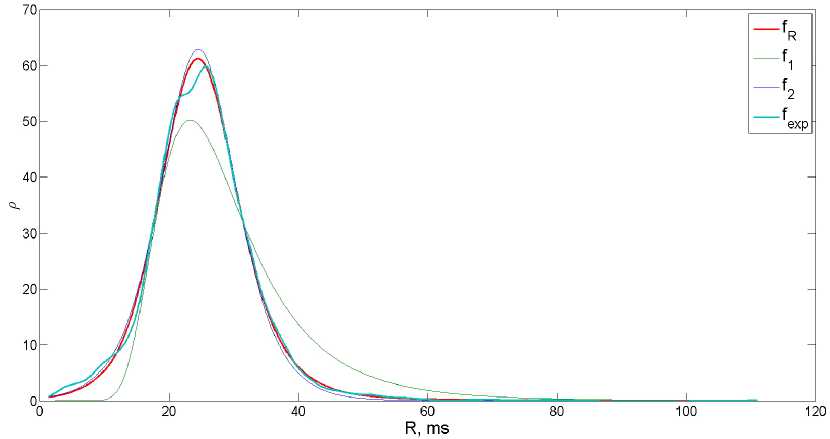
Рис. 8. Ядерная оценка плотности и оценки смеси для т = 9 . 615

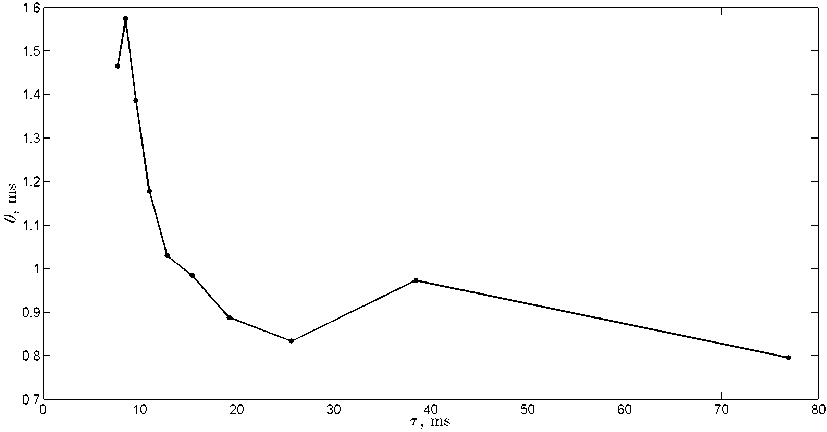
Рис. 9. Оценки порогового параметра Ө(т )

Выражение (12) содержит плотности f i и / 2 с параметрами, подлежащими оценке, а также коэффициенты W j , которые априори неизвестны. Так как известно количество компонентов смеси, то для оценки коэффициентов и параметров распределений используем EM-алгоритм [13].

На рис. 8 приведен результат действия алгоритма для т = 9.615 . Как можно легко видеть, полученная оценка плотности близка к ядерной оценке плотности на основе экспериментальных данных.

На рис. 9 представлены оценки порогового параметра 0 , полученные для различных т . По приведенным данным видно, что значения 0 растут при уменьшении т , однако абсолютное изменение не превышает 0.8 мс.

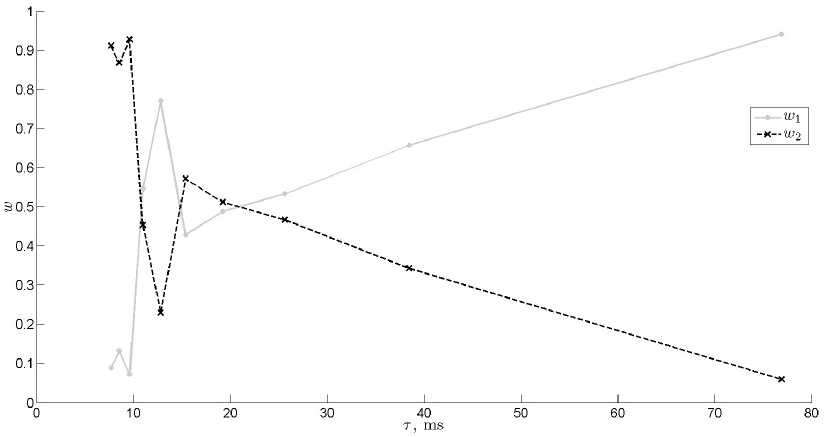
Рис. 10. Оценки коэффициентов смеси w i ( t ) и w ₂( t )

На рис. 10 представлены оценки коэффициентов w i и W 2 смеси (12), полученные для различных т . При малых т доминирует логистическое распределение / 2 , а при больших т — GEV. В промежуточных случаях коэффициенты обоих распределений близки к 0.5. Переход к логистическому распределению происходит достаточно резко, что вполне согласуется с рис. 2 и 3.

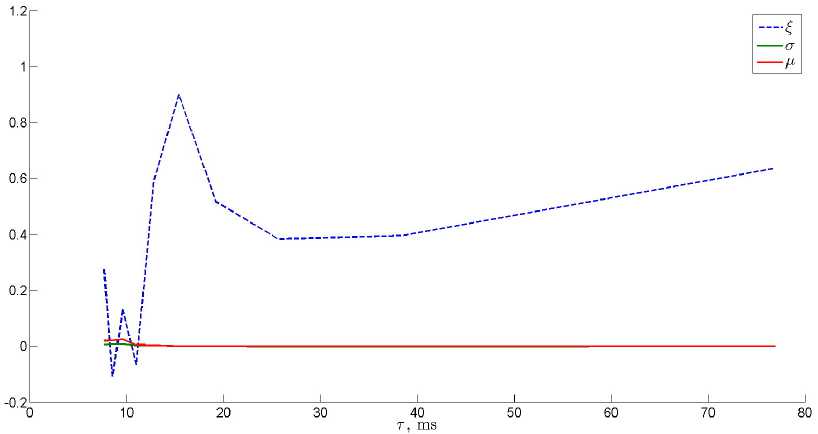
Рис. 11. Оценки параметров GEV к(т ), ст 1 (т ) и л 1 (т )

На рис. 11 и 12 представлены оценки параметров GEV и логистического распределения соответственно, полученные для различных т . Для логистического распределения (11) при малых т существенно изменяется параметр сдвига / 1 . При малых т для GEV меняется тип распределения, определяемый знаком £ : при ^ > 0 это распределение Фреше, а при ^ < 0 -распределение Вейбулла.

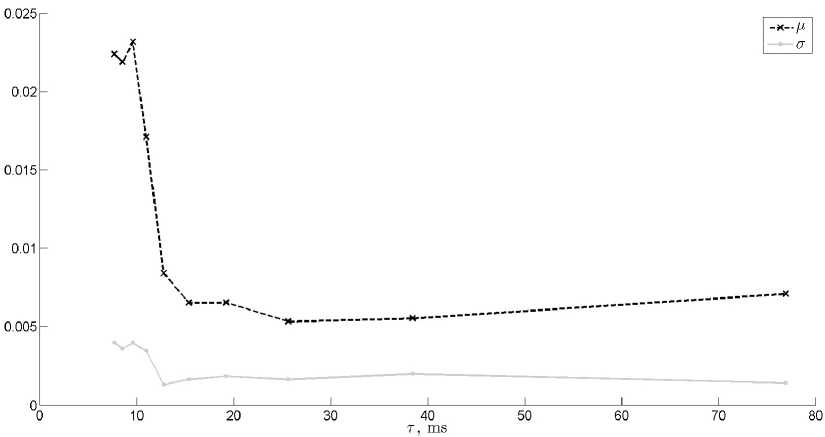
Рис. 12. Оценки параметров логистического распределения / ₂ ( т ) и сг ₂ ( т )

• 6.    Заключение

В статье рассмотрен эксперимент по исследованию зависимости между временем кругового обращения пакета (RTT) и загрузкой сетевого соединения. Полученные результаты подтверждают статистическую зависимость между указанными величинами.

Оценки распределений на основе полученных экспериментальных данных показывают, что распределение RTT может описано в виде выпуклой комбинации двух распределений: экстремальных значений и логистического. При малой загрузке соединения преобладает GEV-распределение, а по мере роста загруженности соединения преобладающим распределением постепенно становится логистическое.

Работа выполнена при поддержке Российского фонда фундаментальных исследований, проекты № 15-37-20611-мол_а_вед и № 13-01-00406-а.