Идентификация структур армирования композитных конструкций на основе результатов экспериментов о гармонических колебаниях

В настоящее время в инженерной практике все более активно используются армированные материалы, позволяющие создавать изделия с уникальными физикомеханическими характеристиками, которых нельзя добиться, используя традиционные конструкционные материалы. Поскольку композитный материал, как правило, формируется в процессе изготовления изделия [1], то окончательные эффективные характеристики конструкции существенно зависят от структуры армирования. На практике, в силу несовершенств технологии, при реализации конкретных структур может произойти отклонение параметров армирования от заданных расчетных значений (например, из-за усадки связующего в процессе его затвердевания). Такое изменение значений параметров армирования приводит к отклонению механических свойств изделия от расчетных значений, задаваемых проектировщиком. Поэтому актуальной является проблема идентификации реально полученных структур армирования композитных конструкций.

В настоящем исследовании предлагается один из возможных методов идентификации параметров структуры армирования, основанный на результатах

динамических экспериментов об установившихся гармонических колебаниях диагностируемой композитной конструкции.

Поскольку рассматриваемая проблема, по сути, является специфической коэффициентной задачей [2], для ее решения рассмотрим уравнения движения при установившихся колебаниях с циклической частотой ш для двух ( m = 1, 2) механических состояний исследуемой конструкции

o ^{( m} ) +p ⁽ m ) w ² u ( m ) = 0, x е V ( i = 1,2,3; m = 1,2 ) , x = { x 1 , x ₂, x 3 }                  (1)

с учетом обобщенного закона Гука о‘"1 = Jum', xеV   (i,J' = 1,2,3; m = 1,2).                                (2)

Здесь нижний индекс после запятой означает частное дифференцирование по пространственной переменной x ( i = 1, 2, 3); по повторяющимся индексам производится суммирование от 1 до 3. Под двумя механическими состояниями здесь и далее понимаются состояния одной и той же композитной конструкции при двух разных структурах армирования; а в общем случае — и при разных материалах компонент композиции [2].

На границе S = SUl] U SО1 ] тела зададим граничные условия uim’| = 0, oj1 »j| = pi1 ] (i = 1,2,3; l = 1,2,..., N),                               (3)

Su                        S О где l — номер варианта нагружения исследуемой конструкции; N — количество вариантов нагружения; oj\ u(m) — амплитуды напряжений и перемещений точек конструкции при установившихся колебаниях; pi1 ] — амплитуды колебаний поверхностно распределенной нагрузки при l-м варианте нагружения. Точки границы SU1 ] считаем жестко закрепленными.

На основании уравнений (1)-(3) и соотношений Коши и /m) + u \m)/

=;m’ =      .         (i, J = !,2,3; m = 1,2),(4)

используя обычную процедуру получения соотношений взаимности для анизотропного тела [2, 3], для каждого l имеем

— u i ¹¹) dS —

UK aS-Aj', )= Xdv+U p l]( u,'2' V

-to ² JJJ ( p ⁽²⁾ —P ⁽¹⁾ ) u*²⁾u^¹’dv = 0      ( l = 1, 2, ..., N ) .

V

Уравнения (5) являются основными в теории коэффициентных обратных задач [2], базирующихся на результатах экспериментов о гармонических колебаниях конструкции. При этом в форме (5) соотношения взаимности справедливы не только в прямоугольной декартовой системе координат Х1, x2, x3, использованной выше лишь для сокращения записи соотношений (1)–(4), но и в произвольной криволинейной ортогональной системе x1,x2,x3.

Для решения задачи идентификации структуры армирования композитной конструкции к уравнениям (5) необходимо добавить структурные соотношения для армированной среды, выражающие эффективную объемную плотность

KK

Р ⁽ " ) = a m ) ( x ) P c + £ p k n k") ( x ) ,    a m) ( x ) = 1 - £ p i’) ( x ) ( " = 1,2 ) ,

k =1                                              k =1

x e V,     x = { x1, x 2, x3} и эффективные жесткости A1") композиции через параметры армирования: цk"), vk") — плотность и угол армирования волокнами k-го семейства в m-м состоянии (отсчитываемый, например, от направления x1 в тонкостенной конструкции). Здесь K — количество семейств арматуры; pc, pk — объемные плотности материалов связующего и арматуры k-го семейства.

Если эффективная объемная плотность композиции однозначно определяется соотношением (6), то в рамках разных структурных моделей механического поведения армированной среды для эффективных жесткостей A_i ⁽ _jr ^m _n ⁾ получаются разные функциональные зависимости

A " ) = A " ) ( v , ц ) , V = { V 1 , V 2 ,..., V K } , Ц = { Ц 1 , Ц 2 ,..., Ц K } .                     (7)

При решении столь сложной проблемы как задача идентификации структур армирования композитной конструкции естественно ориентироваться на наиболее простые структурные модели, удобные с точки зрения последующего анализа и учитывающие основные особенности волокнистой среды. В случае идентификации структур армирования тонкостенных конструкций (наиболее часто используемых на практике), подчиняющихся гипотезам Кирхгофа–Лява, или в случае безмоментного деформирования таких конструкций можно использовать следующие структурные соотношения для полиармированного слоя [1], удовлетворительно согласующиеся с экспериментальными данными [4]:

K

A*”> = Г>Ei + £Ekv£>lkГфИ")    (i, j, r, n = 1, 2), к=1

a ^-1=l-v², a = Na ., a^-1=2(l + v) iiii                    , iijj iiii , ijij

( j = 3 - i ;     i = 1,2),                       (8)

Если в (8) принять E = 0, то получим структурные соотношения в рамках нитяной модели. Могут быть использованы и более сложные структурные модели волокнистой среды [5, 6 и другие]. Заметим, что в рамках предлагаемого метода идентификации выбор той или иной структурной модели не принципиален, но чем точнее модель соответствует экспериментальным данным, тем точнее будут результаты реконструкции структуры армирования при проведении реальных экспериментов.

Задача об определении параметров армирования ц _k , v _k может быть решена лишь при наличии дополнительной информации. В настоящем исследовании в качестве такой информации будем использовать:

u.\ S o 1 ] = fi ^[ l ^] ( x , ^ю) , x ^е S О ^{1 ]}, ^юе [ ^ю 1 , ® 2 ] (¹ = 1,2,3, l = 1,2,..., N ) , (9)

где f ^{[ 1 ]} — известные из эксперимента значения амплитуд перемещений на той части границы S а ^{1 ]} конструкции, на которой заданы квазистатические граничные условия (3) при l -м варианте нагружения. Также предполагается, что при каждом варианте нагружения циклическая частота изменяется в пределах (т < и < и ₂.

Как видно из структурных соотношений (7), (8), задача определения параметров армирования ц _k , v _k является нелинейной и может быть решена с использованием итерационного процесса, на каждом этапе которого осуществляется решение линейной задачи. Полагая

ц^2’ = ц® + Aц к,   vk2) = v k’’ + Av k,   u = u® + Au, e j2) = ej + Ae .,

, x                                                                      (10)

< = A 1) +A A_ u ( ²⁾ ( S ^] ) - f ^{[ l ]} ( S [ ^{l ]}, и )     ( i , j , r , n = 1, 2, 3 )

и сохраняя в уравнении (5) линейные по Ац _k , Av _k слагаемые, с учетом (6), (7) (а для конкретной модели полиармированного слоя также выражений (8)) и дополнительного условия (9) для тонкостенной конструкции толщиной 2 h , квазиоднородно армированной в поперечном направлении ( ц к ¹3 = 0, v_k 3 = 0, A .П ₃ = 0), получим

ЛЕ [ K i ^k ) ( x 1 , x 2 ’ ^И)^A Ц k ⁺ K v ^k ) ( x 1 ’ x 2 ’ ®W k ] d^A =

G k =1

=- JJ p [ ^{l ]} ( f ^{[ l ]} - u? ) A - J] p ( f ^{[ l ]} - u *") dA ^-- G ^{( +}                                              G ^{( - )}

где

- J J P^{[l ]} ( f^{l ]}

г^{[ 1 1} - h o

- u^ 1 ) dx₃ d Г ,

roe [ ro ₁, и ₂ ] ( l = 1,2,..., N ) ,

h

( ^k)(x             fa(¹⁾a ( ¹⁾ - Aijr^dx

K v ^{( x} 1 , x 2 ’ ^{и )} j ^e j ^e rn dv (1) dx 3 ,

h

^K ц ^k ) ( ^x 1 ’ x 2 ’ ^и ) = J

- h

P(V)p(V)      irm

e j ern 5ц®

го ² u®u i^ ( p k ^- p _c ) dx 3 ;

dA, dA(+), dA(-) — элементы площади срединной, а также верхней (+) и нижней (-) лицевых поверхностей тонкостенной конструкции; G, G(+), G(-) — области, занимаемые этими поверхностями; Г^] — часть контура, ограничивающего область G, соответствующая торцевой поверхности, на которой заданы статические граничные условия; x3 — поперечная координата, равная по модулю расстоянию от произвольной точки конструкции до ее срединной поверхности; x1, x2 — координаты точек срединной поверхности.

Если, как это обычно делается в теории деформирования элементов тонкостенных конструкций, используются те или иные кинематические гипотезы (например, Кирхгофа, Тимошенко [7], Амбарцумяна [8] или соответствующие другим неклассическим теориям [1, 6] и подобные), то входящие в (11), (12) интегралы по переменной x ₃ могут быть вычислены.

Пусть прямые граничные задачи (1)–(3) (или соответствующие им задачи теории пластин и оболочек [1, 6–8]) с учетом известных соотношений (7) (и, в частности, (8)) при m = 1 и I = 1,2,..., N решены (что может быть осуществлено эффективно на основании, например, методов конечных разностей или конечных элементов). Тогда равенства (11) можно трактовать как систему интегральных уравнений Фредгольма 1-го рода относительно функций Др _к ( x 1 , x ₂ ) , Ду _к ( x 1 , x ₂ ) с известными ядрами (12) и известными правыми частями. При этом в начале итерационного процесса (10), (11) в качестве исходного приближения для ц^, у ^ могут быть выбраны их проектные значения.

Так как система (11) состоит из N уравнений и содержит 2 K неизвестных функций Дц _к , Ду _к ( к = 1, 2,..., K ), то для ее замыкания необходимо потребовать, чтобы N = 2 K . Следовательно, для решения задачи идентификации структуры армирования тонкостенной конструкции, усиленной K семействами волокон, необходимо проведение серии экспериментов о ее гармонических колебаниях при 2 K независимых вариантах нагружения.

В силу того, что выше нигде не использовались условия постоянства поперечных сечений волокон [9] (функции ц к™ ) , У к™ ) предполагались независимыми), полученные результаты справедливы лишь для волокон переменного поперечного сечения. На практике же, как правило, используются волокна постоянного поперечного сечения, для которых параметры армирования ц к™ ) , у к™ ) связаны соотношением [9]

( A ₂ ц к™ ) cos У к™ ) ) 1 + ( A ₁ ц k™ ) sin У к™ ) ) ₂ = 0 ( к = 1,2,..., K ) , ( x 1 , x ₂ ) е G , | x ₃| <  h ,    (13)

где A ₁ , A ₂ — параметры Ламе для срединной поверхности.

Если траектории армирования — углы у к™ ) , заданы, то для однозначного интегрирования уравнения (13) относительно ц к™ ) на части (обозначим ее Г _к ) контура, ограничивающего область G , на которой волокна k -го семейства входят в конструкцию, необходимо задать краевые условия [9]:

ц к™ ) ( n 1^C oS у к™ ) ⁺ n 2^sin у к™ ) ) = ^П к (^Г к ) , ( ^x 1 , ^x 2 )^еГ к ( 1 <  ^к <  ^K ) , I ^х з| <  h ,          ⁽¹⁴⁾

где n 1 , n 2 , n 3 = 0 — компоненты вектора единичной нормали к торцевой поверхности конструкции; О _к ( Г _к ) — функция, пропорциональная количеству арматуры к -го семейства заданного поперечного сечения, входящей в конструкцию через единичную площадку торцевой поверхности [9]. Предполагается, что О _к ( Г _к ) известны из конкретной реализации технологического процесса намотки или выкладки композитной конструкции армирующими волокнами.

Линеаризовав соотношения (13), (14) с учетом разложений (10), получим

⁽ A^ „ cos у? )_j+⁽      k sin у? )_д ^{- (} A ² . k _Ц--_$1П .                               (15)

+ ( A 1 Ay _к p^cosy^ ) = 0    ( к = 1,2,..., K ) , ( x 1 , x ₂ ) e G ;

( n 1 cos y^ + n ₂ sin y ^ ) Ap _к + p^ ( - n 1 sin y^ + n ₂ cos y^ ) Ay _к = 0,

( x 1 , x ₂ ) еГ _к ( к = 1,2,..., K ) .

Таким образом, в случае армирования композитной конструкции волокнами постоянного поперечного сечения соотношения (11) представляют собой систему интегральных уравнений Фредгольма 1-го рода, в которой на неизвестные функции Ap _к , Ay _к наложены дифференциальные связи (15) при краевых условиях (16). Теперь разрешающая система (11), (15) состоит из K + N уравнений и содержит 2 K неизвестных функций Ap _к , Ay _к ( к = 1, 2, ..., K ), поэтому для ее замыкания необходимо потребовать выполнения равенства N = K . Следовательно, для решения задачи идентификации структуры армирования тонкостенной конструкции, армированной K семействами волокон постоянного поперечного сечения, необходимо проведение серии экспериментов о ее гармонических колебаниях при K независимых вариантах нагружения.

В частном случае тонкостенных конструкций типа оболочек вращения и кольцевых пластин с осесимметричными структурами армирования, то есть не зависящими от окружной координаты x ₂ , система (11), (15) может быть упрощена. Действительно, при этом из соотношений (13), (14) (если учесть n 1 = ± 1, n ₂ = 0) имеем [9]:

p k" ) (У = П . kl [ R ( x , ) cos у ⁽ m ) ( x , ) ] ( к = 1,2,..., K ) ,                               (17)

где R ( x 1) — расстояние от точек срединной поверхности до оси вращения (в случае кольцевых пластин R ( x 1 ) = x 1 — полярный радиус); О , _к — постоянные, которые известны, как и О _к в (14), из конкретной технологии армирования.

Из равенств (17) с учетом разложений (10) получаем:

Ap _к ( x 1 ) = Q , _kR ^{- 1} ( x 1 ) sin y® ( x 1 ) cos ^{- 2} y® ( x 1 ) Ay _к ( x 1 ) ( к = 1,2,..., K ) .          (18)

Подставим (18) в уравнения (11), и тогда

K

JJ Z K ⁽ k ) ( x i , ^X 2^, ® ) ^A v k ( X ) ^dA = - JJ p i ^{l ]} ( fi ^{[ l ]} - u? ) ^{dA ( + )} - JJ p i ^{l ]} ( fi ^{[ l ]} - ^u(i ) ^{dA ( - )} -

G k=1                                                  G(+)

Гh                    1

-J j p ^{[ l ]} ( f ^{[ l ]} - u ⁽¹⁾ ) dx₃ d Г     ( l = 1,2,..., N ) ,      oe [ o , to₂ ] ,

ГЯД             J где

K(k) = K(k) (Xi, x2, m)Q*kR-1 (Xi)siny^ (Xi)cos-2 y® (x) + Kyk) (Xi, x2, to);(20)

функциям K P ^k ) , K y ^k ) соответствуют выражения (12). При этом в структурных соотношениях (7) (и, в частности, в (8)) нужно учесть зависимости (17).

При N = K равенства (19) представляют собой замкнутую систему уравнений Фредгольма 1-го рода с гладкими ядрами K ^{( k )}, то есть интегральные операторы, стоящие в левых частях равенств (19), являются непрерывными [2]. Поэтому после дискретизации системы (19) получаем плохо обусловленную систему линейных алгебраических уравнений относительно узловых значений функций Ay _k ( X 1 ) , решение которой требует применения регуляризующих алгоритмов [2, 10]. Подобные рассуждения справедливы и для интегральных операторов в левых частях равенств (11).

В качестве примера рассмотрим задачу идентификации структуры армирования тонкой цилиндрической оболочки радиуса R = 0,2 м, толщиной 2 h = 0,5 см и длиной L = 1 м ( A 1 = A ₂ = 1), изготовленной из алюминиевого сплава АД ( E = 71 ГПа, v = 0,31, p _c = 2710 кг/м³ [11]). Оболочка армирована меридионально-симметрично двумя семействами борных волокон ( у 1 ( X 1 ) = -y ₂ ( X 1 ) , р 1 ( X 1 ) = ц ₂ ( X 1 ) , E 1 = E ₂ = 410 ГПа, v 1 =v ₂ = 0,23, P j = р ₂ = 2550 кг/м³ [11], K = 2). Проектные значения параметров армирования:

р k (Xi ) = p k = 0,2, yk (Xi ) = y 0 =-(-1) k п/6   (k = 1,2), 0 < Xi < L .(21)

На основании (21) в соотношениях (17), (18) имеем известные значения

Qtk = Rрk cos У 0 = const   (k = 1,2), П., =Qt2.(22)

Для тестирования разработанного алгоритма идентификации структуры армирования в условиях псевдореального эксперимента [2] зададим псевдореальные (якобы полученные в реальности) значения углов армирования в виде:

У1 (X1 ) = -y2 (Xi) = п[(L-X1)/5 + X1 /4J /L, 0 < X1 < L .(23)

При этом псевдореальные плотности армирования p _k вычисляются по формуле, аналогичной (17), с учетом (22), (23).

Идентификацию будем проводить на основании результатов экспериментов о продольных и крутильных гармонических колебаниях тонкой цилиндрической оболочки, находящейся в безмоментном напряженном состоянии. Соответствующие прямые двухточечные граничные задачи определяются уравнениями

(А,_ии_п ) + рш² и = 0 G = 1,2), 0 <  х . <  L , шеГш. , ш,1

1 i 1 i i ,1 ₁                   i                                                         1                                1        2

и граничными условиями и (х, ) = 0,    A.. . (х,,) и. (х„ ) = р.[l]   (i = 1,2; l = 1,2,..., N)

i \ * /      "       1 i 1 i \ ** / i ,1 \ ** / 1 I \                       777 J

х * = 0, х ** = L или     х * = L , х ** = 0.

Отсюда при i = 1 получаем задачу продольных, а при i = 2 — крутильных колебаний цилиндрической оболочки. Для конкретности коэффициенты A _{1 i 1 i} будем определять по структурным формулам (8).

Решая прямые задачи (24), (25) при разных ω с учетом (6), (8), (17), (23), на основании соотношения (9) получим псевдореальные значения функции f ^{[ 1 ]} ( х ** , ш ) , используемые далее в качестве дополнительной информации в задаче идентификации.

Для каждого из исследуемых случаев система (19) редуцируется в одно уравнение Фредгольма 1-го рода

L

J К , ( х ^ ш) Ау 1 ( х ) dх_x = - р ^{[ 1 ]} [ fi ^{[ 1 ]} ( х ** , ш ) - и ⁽¹⁾ ( х ** , ш ) ] ,

ше [ ш 1 , ш ₂ ]     ( l = 1,2,..., N ;    i = 1,2 )

с гладкими ядрами K i ( х 1 , ш ) , имеющими выражения

К1 (X, ш

¹ ) = 2 ц * 1 ( и # ) 2 ( ^cos⁴ у ⁽¹⁾

Eauu ) ^- ( ^{ш и} 1 ⁽¹⁾ ) 2 ( Р 1 ^- P c ) sin V ^{(1) х}

х cos ² у (1) - 8 Е 1 ц *1 ( и® ) sin у (1) cos² у (1) ,

К ₂ ( х 1 , ш

।) = 2 ц *1 ( и 211 ) 2 ( E 1 sin² v ⁽¹⁾ cos² V ⁽¹⁾

^Ea 1212 )  ^{( ш} u 2 ^) ^{( p} 1    ^P c )

х

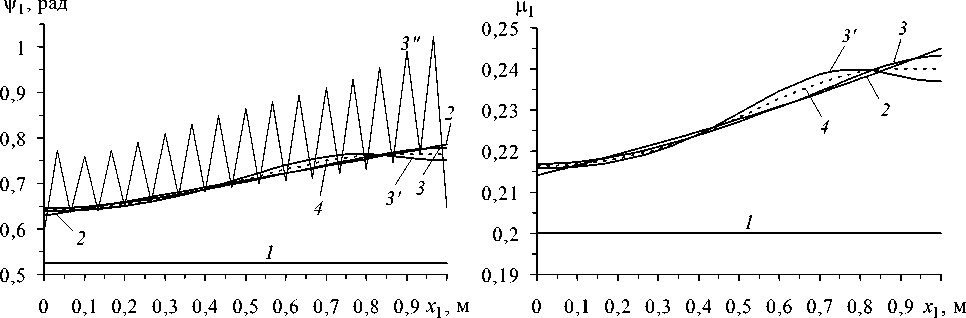
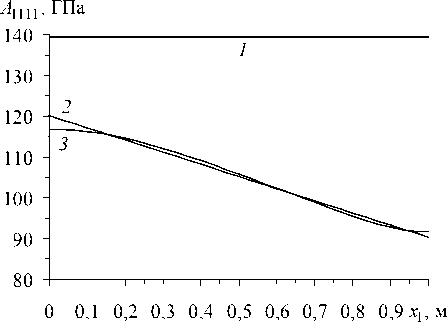
На рисунках 1 и 2 приведены результаты модельного численного эксперимента по восстановлению функций у 1 , ц 1 , A 1111 , A 1212 . На этих рисунках горизонтальные прямые 1 соответствуют проектным значениям (21), (8) указанных функций, линии 2 — псевдореальным значениям (см. (8), (17), (22), (23)), остальные линии представляют результаты восстановления этих характеристик. Кривые 3 , 3' на рисунке 1 построены на основе разработанного метода и дополнительной информации, полученной, соответственно, из проведенных экспериментов по продольным и крутильным установившимся колебаниям цилиндрической оболочки.

Так как рассматриваемая задача идентификации является некорректной [2, 10], то для ее численного решения использовался алгоритм регуляризации по методу Тихонова [2, 10, 12] (конечномерная аппроксимация интегральных уравнений Фредгольма 1-го рода с гладким ядром типа (26), (27) в предположении, что из априорных соображений известно, что А^ 1 ( х 1) — кусочно-гладкая функция, приведена в [2]). Параметр регуляризации α выбирался из условия его квазиоптимального значения [12]; на каждой итерации получалось свое значение α, имеющее порядок 10²...10³.

а                                        б

Рис. 1. Реконструкция структуры композитной оболочки: углов ( а ) и плотностей ( б ) армирования

а

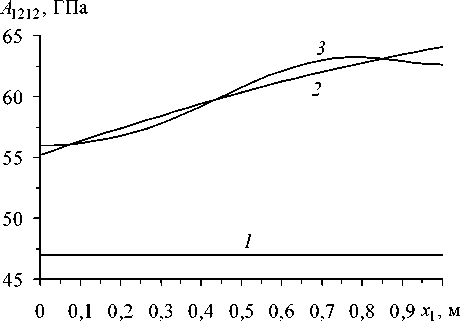
Рис. 2. Реконструкция эффективных модулей упругости оболочки: продольного ( а ) и сдвигового ( б )

б

Кривые 3 , 3’ на рисунках 1, 2 построены по результатам шести итераций итерационного процесса (10), (26), (27). Дальнейшее увеличение числа итераций не приводит к принципиальному уточнению решения задачи идентификации. Сравнение между собой кривых 2 и 3 на рисунках 1 и 2, а свидетельствует о хорошей реконструкции рассматриваемых функций ^ 1 , ц 1 , A 1111 на основе результатов экспериментов по продольным колебаниям оболочки. Сопоставление же кривых 3' (Рис. 1) и 3 (Рис. 2, б ) с кривыми 2 на этих рисунках демонстрирует несколько худшую, но вполне удовлетворительную точность реконструкции функций ^ 1 , ц 1 , A 1212 на основе результатов экспериментов по крутильным колебаниям рассматриваемой тонкостенной конструкции. При этом точность реконструкции эффективных модулей упругости композиции A ₁₁₁₁ , A ₁₂₁₂ (см. Рис. 2) имеет порядок точности используемой структурной модели механического поведения армированного слоя [4].

Так как заранее реальная структура армирования не известна и имеются результаты идентификации одной и той же структуры по двум независимо проведенным экспериментам, то естественным является усреднение этих результатов. Пунктирные кривые 4 на рисунке 1 соответствуют такому усреднению. Видно, что они хорошо согласуются с кривыми 2 , поэтому результаты реконструкции можно считать вполне приемлемыми.

На рисунке 1, а ломаная линия 3'' приведена для сравнения с линией 3 и соответствует решению той же задачи идентификации после двух шагов итерационного процесса (10), (26), (27) без использования метода регуляризации Тихонова (при увеличении количества итераций сходимость итерационного процесса в этом случае нарушается). Поведение ломаной 3'' наглядно свидетельствует о некорректности рассматриваемой задачи идентификации структуры армирования и о необходимости применения при ее решении регуляризующих алгоритмов.

Отметим, что выше были получены результаты идентификации структуры армирования на основе решения прямых граничных задач (24), (25) при первом ( l = 1) варианте нагружения цилиндрической оболочки, когда предполагалось, что х , = 0, х„ = L . Можно получить аналогичные результаты реконструкции и при втором ( l = 2) варианте нагружения такой конструкции, а именно, при х , = L, х ,, = 0, то есть при жестком закреплении правой кромки оболочки и приложении нагрузки к левой кромке. Результаты реконструкции структуры армирования при таких вариантах нагружения и закрепления конструкции не приводят к принципиальному уточнению решения задачи идентификации. В силу этого и с целью незагромождения рисунков соответствующие расчетные кривые не приводятся.

Таким образом, полученные результаты показывают, что предложенный здесь метод идентификации структур армирования тонкостенных композитных конструкций на основе проведения экспериментов по их гармоническим колебаниям дает вполне удовлетворительные результаты реконструкции и может быть использован на практике.

В заключение отметим, что развитая в настоящем исследовании теория базируется на допущении, что отклонения реальных эффективных характеристик композитной конструкции от их проектных значений обусловлены только неточностью реализации проектной схемы армирования в процессе изготовления изделия. В действительности же, кроме указанной, могут существовать и другие причины таких отклонений: пористость связующего; его неоднородность; незнание точных значений упругих констант материалов компонент композиции; возникновение в окрестности границы связующее–волокно переходных зон со своими характеристиками (например, интерметаллидных в металлокомпозитах) и так далее. Обобщая развитые в [2] и в данной работе подходы, можно создать методы реконструкции и других параметров и характеристик элементов конструкций из армированных материалов. Изучение этих вопросов выходит за рамки настоящего исследования.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 10-01-90402_Укр_а) и Президиума СО РАН (Постановление № 10 от 15.01.09, проект № 72).