Игра с «линией жизни». Случай поточной встречи

Предположим на плоскости задано некоторое множество S . Две точки – преследователь P и преследуемый E , обладая ограниченными по модулю линейными скоростями, перемещаются в множестве S , имея при этом возможность в каждый момент времени изменять направление движения (простое движение). В начальный момент времени игроки находятся во множестве S . Преследуемый E считается пойманным, как только расстояние между ним и преследователем P достигнет значения, меньшего или равного l ( l >  0 ) . Число l называется радиусом встречи, а процесс поимки - l -встречей. Целью игрока P является поимка игрока E до достижения последним «линии жизни» – границы множества S . Игрок E преследует противоположную цель, т. е. стремится достичь «линии жизни» до l -встречи.

Будем рассматривать игры с дискриминацией игрока E , в которых E использует кусочно-постоянные стратегии va е E, а P использует стратегии с дискриминацией из P+ (и). Стратегией с дискриминацией (констратегией) игрока Р называется любая вектор-функция u1 ( t, x1, У1, x 2, У 2, V ), u 2 ( t, x1, У1, x 2, У 2, V ) ’ u = {u1, u 2} = <

определенная для всех t >  0, x 1 , y 1 ,x 2 ,y 2 и векторов v = { v 1 , v ₂ } , v 1 ² + v ₂ ² <  в ² , а также удовлетворяющая условию u 1 ² + и 2 <  а¹ (P+ – множество всех констратегий игрока Р ).

Пусть z 1 ( t ) ( z 2 ( t ) ) траектория игрока P ( E ) в ситуации { u , v ^ } e P+ x E, ис

ходящая из начальной точки z0 (z2), и пусть tE = inf {t: z2(t) e S} , tP = min {t: p (z1(t), z2 (t)) < l} (если таких tP не существует, то tP полагаем равным ∞). Тогда выигрыш игрока Е равен:

K ( z i , z 2 , u , v _CT ) =

- 1, 5A8 t p <  t S , t p <« , • 0, 5A8 t_p = t S = » ,

1, 5A8 t_p >  t S , t S <« .

Определение 1. Выигрывающим множеством WP (WE) игрока P(E) называется множество всех точек {z1; z2 }e R4, таких, что min max K(z1, z2, u, vCT) = -1 u∈P+ vσ ∈E

ВЕСТНИК Мордовского университета | 2014 | № 1-2

( max min K ( z 1 , z ₂, u, v _CT ) = + 1 ). v σ ∈ E u ∈ P ⁺

Таким образом, если преследование начинается из точек z ₁ , z ₂ , удовлетворяющих условию { z 1 ; z 2 } e W , то игрок Р всегда может поймать игрока Е до достижения им «линии жизни». Аналогично, если преследование начинается из точек, таких, что { z 1 ; z 2 } е W E , то игрок Е может достичь «линии жизни» до момента l -встречи независимо от действий преследователя.

Определение 2. Сечение W P ( z 0 ) выигрывающего множества W P с R ⁴ игрока Р плоскостью z 2 = z 0 - зоной встречи в позиции z 2 , а сечение W E ( z 0 ) выигрывающего множества W E с R ⁴ плоскостью z 1 = z 0 называется зоной убегания в позиции z ₁ ⁰ .

Зоны встречи и убегания, являющиеся множествами на плоскости, дают более наглядное представление о воз- можностях игроков, чем выигрывающие множества в четырехмерном пространстве.

Пусть u – некоторая фиксированная стратегия игрока Р , обладающая свойством в любой ситуации { u , v y } е P+ х E обеспечивать l -встречу с игроком Е во всей плоскости, если в момент времени t = 0 игроки находятся в точках ^z 0 = ( x p о ; y_P о ) , z 0 = ( ^x e о ; y_E о ) .

Обозначим через Cu (z”, z0) множество всевозможных положений игрока Е в момент l -встречи в ситуации {u, vCT} для различных vσ ∈ E (местоположение игрока Е в момент l -встречи называется «точкой встречи»). Очевидно, что если множество Cu (z1, z2) имеет непустое пересечение с дополнением множества S, то игрок Р, используя стратегию u , не может гарантировать l -встречи с игроком Е в множестве S.

Определим структуру множества Cu (z0, z0), c тем чтобы получить уравнения границ зоны встречи и зоны убегания. Имея явное выражение для границ множества Cu (z0, z0) и зная границу множества S, можно геоме- трически достаточно просто построить границу выигрывающего множества игрока Е в позиции P0 = z0 как множество точек z2 е 5 , для которых граница множества Cu (z“, z2) касается границы множества S. Аналогично, имея явное выражение для границы множества Cu (z“, z0) и зная границу множества S, можно геометрически построить границу выигрывающего множества игрока P в позиции E0 = z0 как множества точек z1 е 5 , для которых граница множества Cu (z0, z0) касается границы множества S.

Приведем решение игры в случае поточечной поимки (l = 0) в предположении, что игроки движутся с макси- мальной скоростью. Ясно, что игроки P и Е, преследующие противоположные цели, должны использовать все свои возможности, в частности, они должны двигаться с максимальной скоростью. В этом случае уравнения движения имеют следующий вид:

X1 = Ui, У1 = u 2, Ui + u 2 = a , x2 = V1 , y! = v2, v2 + v2 = P2 .

Будем считать, что скорость преследователя больше скорости убегающего ( a > в ) , в противном случае всегда выигрывает игрок Е.

Известно, что если Е выбирает любое прямолинейное движение, то при параллельном сближении множество точек встречи являются окружностью Аполлония – границей круга

Р ( z , z 0 ) w >  р ( z , z 0 ) , w = в / a , [1]:

• ⁵ 0 = { z P ⁽z , z ° ) w = P ⁽z , z ^{0 )} } .

Пусть K – «линия жизни». Рассмотрим семейство окружностей

{ C ⁽ a , p ⁽ z_x,a ) w ) } a_eK          ⁽¹⁾

с центрами на «линии жизни» и радиусами. Огибающей (или расширенной огибающей) семейства (1) будем называть кривую, которая в каждой своей точке касается хотя бы одной окружности C(a,p,(z 0 ,a)w), a e K .

Теорема [1]. Если граница F ( z 1 ⁰ ) зоны убегания W E ( z 1 ⁰ ) является гладкой кривой, то она совпадает с частью огибающей семейства (1).

Пусть «линия жизни» является гладкой и задана параметрически

K : x = x ( t ), У = У ( t ), t e [ 1 1 , 1 2 ] , (1)

тогда огибающая семейства определяется системой уравнений:

Серия «Естественные и технические науки»

F ( x , y , t ) = ( x - x ( t )) ² + ( y - y ( t )) ² - w ² [( x ⁰ - x ( t )) ² + ( y 0 - y ( t )) ² ] = 0,

• — ¹ F ( x , y , t ) = dx^t) ( x - x ( t )) + dy^ ( y - y ( t )) + w ² [ dx^ ( x ( t ) - x 1 ) +      O')

L 2                dt                dt                    dt                      V-)

+ dy ^ t ) ( y ( t ) - y 0 )] = 0.

dt w2

Пусть К - прямая, z ^ = { 0; b } ,                      У 2 ^- 1 — ^ Т ^x 2 = ^w 2 b ²,

K : x ( t ) = t, y ( t ) = 0, - да <  t < +да .

Система (2) имеет вид

( x - 1 ) ² + y ² = w ²( t ² + b ² ),

— ( x + t ) = wt.

Исключим параметр t ( t = x / (1 - w ² )):

Итак,

y

x

—

w ² b ² ( 1

y

—

w ² b ² ( 1

—

w ² ) b²

x

—

w ² ) b²

= 1.

= 1.

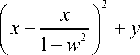
= w

(

x ²

K- - w ² ) ²

^

^{+ b 2}

)

w

( 1 - w ² ) 2

x + y

w

( 1 - w ² ) 2

x + w b ,

Огибающая (3) является гиперболой при b≠0 и вырождается в пару прямых при b = 0 (рис.1). Огибающая (3) совпадает с границей зоны убегания W E ( z 1 ⁰ , K ) .

Направленная вверх ветвь гиперболы (3) совпадает с границей зоны убегания W E ( z 10 ,CS ) в игре с «линией жизни»

в полуплоскости 5 ( -да <  x < +да , у >  0) .

Заметим, что абсцисса точки касания окружности Аполлония для началь- равна x= xE 2 .

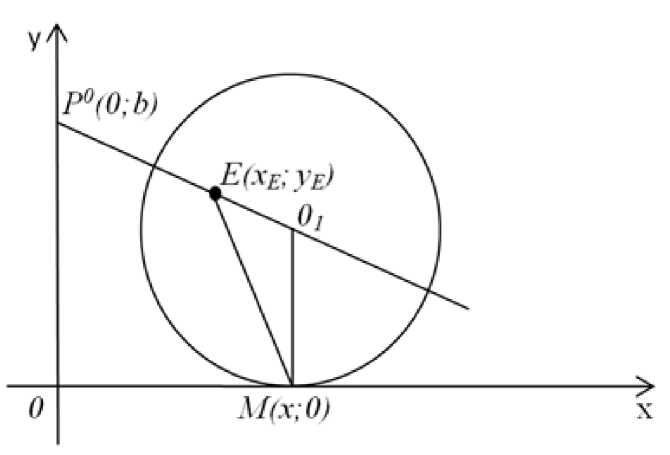
Рис. 1.

Аналогично можно показать, что при поточечной поимке зона встречи W P ( z 2 ) ( z 0 = { 0; 6 } ) совпадает с областью, ограниченной эллипсом 22

*    +=

• 1    — w A21

b2

w2

ных положений z 0 = { 0; b } , z 2 = { x E ; y_E }

Внутренняя часть эллипса, лежащая в полуплоскости S, является выигрывающим множеством игрока P в позиции E ⁰ (рис. 2). Заметим, что в данном случае абсцисса точки касания окружности Аполлония для начальных положений w ²

z i = { x p ; y p } , z 0 = { ⁰ ; b } x = -      2 x p .

• ²                 1 - w

  ВЕСТНИК Мордовского университета | 2014 | № 1-2

  
  
  

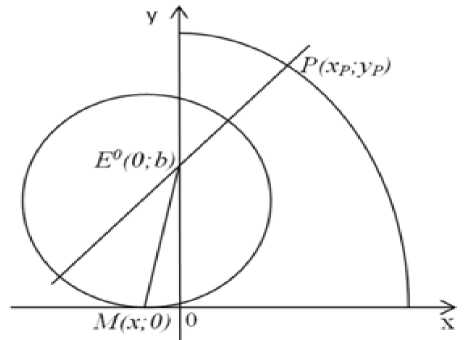
  Рис. 2.

  
  

Рассмотрим случай, когда S является квадратом

( 5 = { ( x ; y ) | - d <  x <  d, - d <  y <  d } ) .

1) ^s = {( x ; y ) |

- да <  x < +да , 0 <  y <  d } .

В этом случае K - прямая, Z° = {0; 0} ,

K : x ( t ) = t, y ( t ) = d, - да <  t < +да .

Система (2) имеет вид

( x — 1 ) ² + ( y — d ) ² = w ² ( t ² + d ² ), — ( x + 1 ) = w t .

Исключив параметр t ( t = x / (1 - w ² )) , получим

^{( y} - ^d ) 2 -      ^ ____= 1      (4)

w² d ²     ( 1 - w ²) d^{2          1 J}

Направленная вверх ветвь гиперболы (4) совпадает с границей зоны убега- ния WE (z 0, CS) в игре с «линией жизни» в области 5(-да < x < +да, 0 < y < d).

• 2)    S = { ( x ; y ) | - да <  x < +да , - d <  y <  0 } .

Граница выигрывающего множества игрока Е определяется аналогично и имеет вид

( У + d ) ² _ x x ₌₁ w ² d ² ( 1 - w ² ) d ² .

Объединяя оба рассмотренных случая, получаем решение поставленной задачи в полосе -да <  x < +да , - d <  y <  d . Граница выигрывающего множества игрока Е в этом случае имеет вид

Серия «Естественные и технические науки»

⁽ y ± d ⁾²        x^x

---------------------------:--------------------------:--------------- w d (1 - w2) d2

Вид границы выигрывающего множества игрока Е при d=2, w=1/2 приведен на рис. 3.

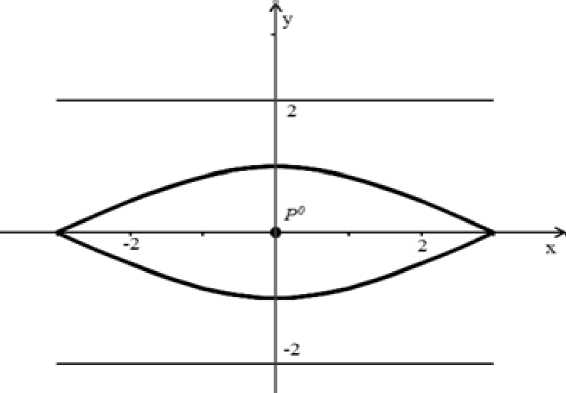
Рис. 3.

3) Рассмотрим случай, когда «линией В этом случае K - прямая, z0 = {0;0} жизни» игрока Е является прямая x= d, т. е. S = {(x;у) | 0 < x < d, -да < у < +да} .           K : x(t) = d, y(t) = t, -^< t < +да.

Система (2) имеет вид d2 + (y - t)2 = w2(d2 + t2), —(y +1) = w21.

^{( x +} d ) ² -     У ²      = 1

w² d ²     ( 1 - w ²) d ²

Исключив параметр t (t = x / (1 - w2)), получим

( x - d ) ²        y²

--------------:---------:---:--------------------------:--------------- w d    (1 - w2) d2

Объединяя оба рассмотренных случая, получим решение поставленной нами задачи в рамках полосы - d <  x <  d , - да <  y < +да . Граница выигрывающего множества игрока E в этом случае имеет вид

Часть полуплоскости S, расположенная правее линии (6), является выигрывающим множеством игрока Е.

4) S = { ( x ; y ) | - d <  x <  0, -да <  y < +да } .

( x ± d ) ²

---:— w² d²     ( 1

= 1.

- w ²) d²

Граница выигрывающего множества игрока Е определяется аналогично и имеет вид

Вид границы выигрывающего жества игрока Е при d = 2 , w = 12 веден на рис.4.

мно-при-

ВЕСТНИК Мордовского университета | 2014 | № 1-2

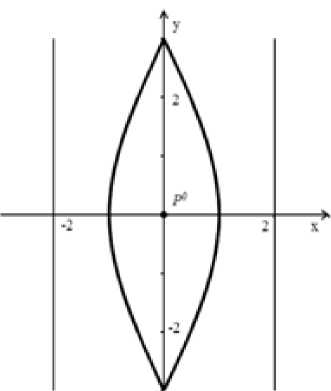
Рис. 4.

Далее решаем игру в квадрате. Граница выигрывающего множества игрока Е в случае 5 = { ( x ; y )| - d <  x <  d, - d <  y <  d } получается как граница пересечения выигрывающих множеств игрока Е, определяемых соотношениями (5) и (7).

Вид этой границы при d = 2 , w = 12 приведен на рис. 5.

Аналогично определяется граница выигрывающего множества игрока P ( ^ 0 = { 0;0 } ).

• 1)    5 = { ( x ; y ) | -да <  x < +да , 0 <  y <  d } .

Зона встречи W P ( z 0 ) совпадает с областью, ограниченной эллипсом

x

^{1 - w}

₂ d ² w

₊ (y - d)L = i.

1₂ d 2 w

• 2)    5 = { ( x ; y ) | - да <  x < +да , - d <  y <  0 } .

Зона встречи WP (z0) совпадает с областью, ограниченной эллипсом случае имеет вид:

x 2	+ ( у+< = L	2 x 2	( у ± d )2 _ +    1 Я2     1. 2 d w	(8)
1 - w 2 2 2 d 2 w	12 d 2 w	1 - w 2 d 2 w

Объединяя оба случая, получаем решение поставленной задачи в полосе

-эт < x < +w, - d < y < d. Граница выиг- рывающего множества игрока P в этом

Вид границы выигрывающего множества игрока P при d = 2 , w = 12 приведен на рис. 6.

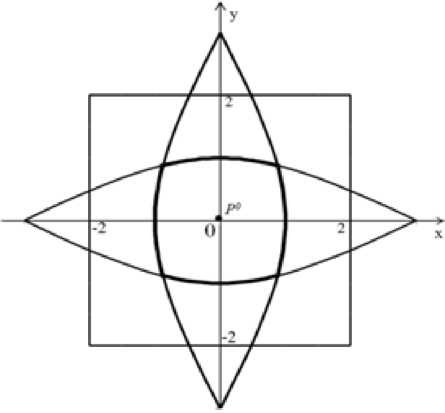
Рис. 5.

Серия «Естественные и технические науки»

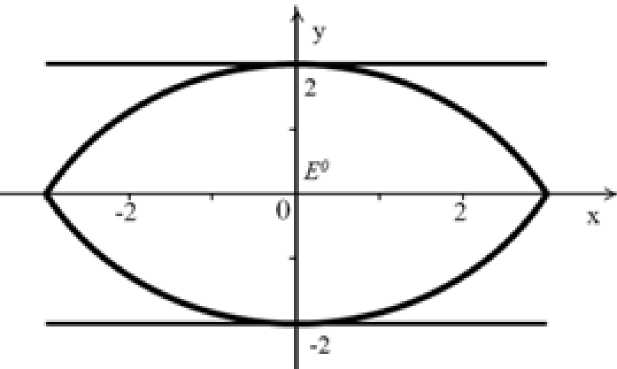
Рис. 6

3) 5 = { ( x ; у ) | 0 <  x <  d, -да <  у < +да } .

Зона встречи W P ( z 0 ) совпадает с областью, ограниченной эллипсом

- d <  x <  d , - да <  y < +да . Граница выигрывающего множества игрока P в этом случае имеет следующий вид:

( * — d ) 2 +

1₂ 2 d w

-^1 = 1.

^ d2

w

( x ± d ) ²

1₂ 2 d

w

+

y

^{1 -} w

2 d ² w

= 1.

4) 5 = { ( x ; y ) | - d <  x <  0, -да <  y < +да } .

Зона встречи W P ( z 0 ) совпадает с областью, ограниченной эллипсом

( x + d ) ²

1₂ 2 d

w

+.

• ^{1    -} w

• 2    d ² w

= 1.

Вид границы выигрывающего множества игрока P при d = 2 , w = 12 приведен на рис.7.

Далее решаем игру в квадрате. Граница выигрывающего множества игрока Рв случае s = { ( x; y )| - d <  x <  d , - d <  y <  d } получается как граница объединения выигрывающих множеств игрока Р, определяемых соотношениями (8) и (9).

Объединяя оба случая получаем решение поставленной задачи в полосе

Вид этой границы при d = 2 , w = 12 приведен на рис. 8.

ВЕСТНИК Мордовского университета | 2014 | № 1-2

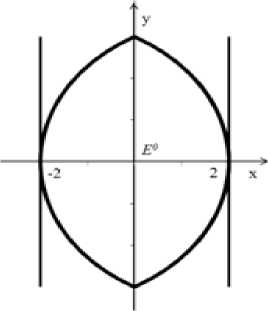
Рис. 7

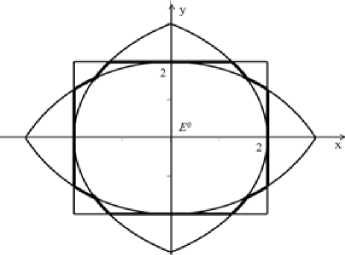
Рис. 8

Поступила 19.12.2013 г.

Об авторах:

About the authors:

Серия «Естественные и технические науки»