Игровая задача импульсной встречи со смешанным ограничением на управление второго игрока
Бесплатный доступ
Рассмотрена игровая задача о встрече в заданный момент времени. На выбор управления первого игрока накладывается импульсное ограничение. Управление второго игрока стеснено геометрическими и интегральными ограничениями. Найдены как условия уклонения, так и условия, обеспечивающие встречу. Построены соответствующие управления игроков.
Короткий адрес: https://sciup.org/147158531
IDR: 147158531
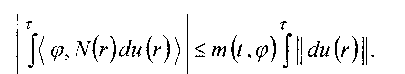
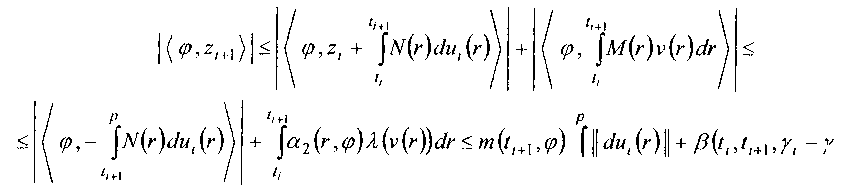
Список литературы Игровая задача импульсной встречи со смешанным ограничением на управление второго игрока
- Красовский, Н.Н. Теория управления движением/Н.Н. Красовский. -М.: Наука, 1970. -420 с.
- Красовский, Н.Н. Об одной задаче преследования/Н.Н. Красовский//Прикл. мат. и мех. -1963.-Т. 27.-Вып. 2.-С. 244-254.
- Красовский, Н.Н. К задаче о преследовании в случае ограничений на импульсы управляющих сил/Н.Н. Красовский, В.Е. Третьяков//Дифференц. уравнения. -1966. -Т.2, № 5. -С. 587-599.
- Ухоботов, В.И. Метод одномерного проектирования в линейной игре с интегральным ограничением и однотипные игры/В.И. Ухоботов//Изв. АН. Техн. кибернетика. -1994. -№ 3. -С. 192-199.
- Ухоботов, В.И. Метод одномерного проектирования в линейных дифференциальных играх с интегральными ограничениями: учеб. пособие/В.И. Ухоботов. -Челябинск: Челяб. гос. ун-т, 2005.-124 с.
- Ухоботов, В.И. Гарантированный стабильный мост в линейной игре импульсной встречи с ограничением на энергетику/В.И. Ухоботов//Рукопись деп. в ВИНИТИ № 3254 -В 87. -Челябинск: Челяб. гос. ун-т. -1987. -20 с.
- Пшеничный, Б.Н. Выпуклый анализ и экстремальные задачи/Б.Н. Пшеничный. -М.: Наука, 1980.-320 с.
- Филиппов, А.Ф. О некоторых вопросах теории оптимального регулирования/А.Ф. Филиппов//Вестник МГУ. Серия «Математика, механика». -1959. -№ 2. -С. 25-32.
- Красовский, Н.Н. Позиционные дифференциальные игры/Н.Н. Красовский, А.И. Субботин. -М.: Наука, 1974. -456 с.
Статья научная
