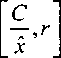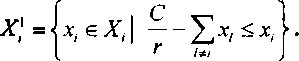Игровые модели коммерческой деятельности кредитных организаций на финансовом рынке олигополии
Автор: Больтогтох Д., Халтар Д.
Журнал: Вестник Бурятского государственного университета. Философия @vestnik-bsu
Рубрика: Математика
Статья в выпуске: 6, 2007 года.
Бесплатный доступ
В этой работе исследуются две игровые модели максимизации доходности каждой кредитной организации, участвующей в конкурентной борьбе на финансовом рынке.
Короткий адрес: https://sciup.org/148178177
IDR: 148178177
Текст научной статьи Игровые модели коммерческой деятельности кредитных организаций на финансовом рынке олигополии
В этой работе исследуются две игровые модели максимизации доходности каждой кредитной организации, участвующей в конкурентной борьбе на финансовом рынке.
Game models of commercial activity of credit organizations on finance market oligopoly
In this work we are investigated two game models maximizing the profit of each credit organization involving in competition on finance market oligopoly.
Введение ой модели предлагается найти гмальное количество кредита х,, z = j,...,a, для /-го банка, когда максимальное значение кредитной ставки г задается Госбанком. Во второй модели основное внимание уделяется рекламе кредитной организации, которая должна привлечь деньги вкладчиков.
Эти две модели базируются на следующих аксиоматических предположениях о коммерческой деятельности кредитных организаций:
-
А) Каждая организация хочет максимизировать свою прибыль, но принятие решений зависит от поведения других.
Б) Они не вступают в договор друг с другом.
-
В) Каждый знает о стратегии других.
Следовательно, эти модели представляют собой некооперативные игры многих лиц, где оптимальные решения понимаются в смысле равновесия Нэша [3, 8,10].
-
§1 . Кредитный рынок с государственной регуляризацией процентных ставок
Пусть на кредитном рынке олигополии ведут коммерческую деятельность N банков (кредитных организаций), где максимальное значение г кредитной ставки задается Государственным банком. Допустим, если /-Й банк предлагает кредит в количестве х,, то рыночная ставка его кредита зависит от г и х = х, +... + х^ следующим образом:
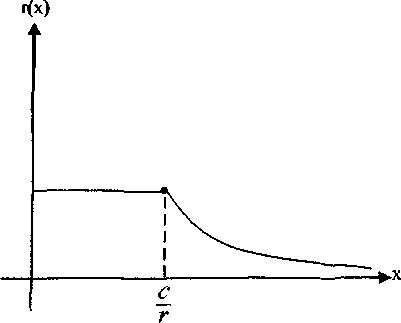
г, = min (—,г ), (1) (х J где С -максимальный суммарный доход, который могут получить банки при достаточно большом количестве х предлагаемых кредитов. Как видим, в этой модели каждый банк не в состоянии установить свою ставку по процентам, она общая для всех и равна
(С ]
r(x) = min(—,г > (см. рис.).
Список литературы Игровые модели коммерческой деятельности кредитных организаций на финансовом рынке олигополии
- Антонов А.В., Поманский А.Б. Рационирование кредитов и алгоритм эффективности распределения заемных средств//Экономика и математические методы. -1994.
- Annual Report, 2004, Bank of Mongolia. Ulaanbaatar
- Воробьев Н.Н. Основы теории игр. Бескоалиционные игры. -М.,1984.
- Дашням Ц. Финансово-кредитные методы регулирования рыночных отношений в Монголии. -2003.
- Чулуунбаатар Н. Вопросы оптимизации управлениефинансовамисредствами коммерческого банка. -Улан-Батор.
- Синки Дж. Ф. Управление финансами в коммерческих банках. -М.: Catallaxy, 1994.
- Sealey, C.W. and Linndley S.T. Inputs; Outputs, and Theory of Production and Cost at Depository Financial Institutions//Journal of Finance, 1977.
- Петросян Л.А, Зенкевич Н.А, Семина Е.А. Теория игр. -М., 1998.
- Чулуунбат О. Бюджетная и денежнокредитная политика Монголии при переходе к рыночной экономики. -Улан-Батор, 2002.
- Морозов Ю.М. Теории игр. -М.: Изд-во МГУ, 2000.