Image Superresolution via Divergence Matrix and Automatic Detection of Crossover

Published Online December 2016 in MECS

Development of new and improvement of existing methods and tools for superresolution digital images that provide effective results process of oversampling image is a challenging problem due to a number of reasons. On the one hand - the prevalence of this type of problems in modern intellectual systems of image processing, and the other - the lack of effective methods for solving this problem in the case of two input images of a scene. Most modern methods to increase the resolution focused on the handling of images with smooth function of intensity, and their adaptation to solve the problem to ensure effective results at high magnification, especially in the case of fluctuation function is far from a complete solution. The complexity of this problem become deep throughout needed to preserve image edges sharpening with the intensity fluctuation function and reduce artifacts and distortions that occur in the input image processing.

Therefore, the urgent task is to develop methods and the development of image superresolution that would ensure qualitative results oversampling at high zoom for images that define the fluctuating intensity function. Images obtained using such methods can be used in many applications, concerning medicine, criminology, remote sensing, and more.

The aim of this article is to modify the method of providing superresolution in the case of two input images by automating determining the factor of crossover operation at each successive stage zooming. For this, in the work describe the task of automatically determining the factor of crossover operation which is solved by solving an optimization problem by criteria built on the continuum of degrees of similarity. The advantages of this approach compared to existing obvious: the possibility of full automation of the method; the selection of the correct values of crossover using solutions of the optimization problem, for efficient work of the method, and so on.

• II.    A NALYSIS OF P REVIOUS S TUDIES

Several classical methods (bilinear, bicubic interpolations) of images resolution increase are characterized by high speed performance. However, they include a number of artifacts that impose restrictions on the practical application of these methods. In addition, they operate just by one image. In some cases, it can be considered as disadvantage. In particular, the presence of several samples of one scene that are aligned relative to each other in partial pixel value carry additional information that could be used for increasing the resolution as well as for improvement of the original sample quality.

One of the possible solutions to this problem is the use of Super resolution reconstruction methods, or superresolution. In general, the super-resolution technology consists of two classes of methods [14], including: optical (OSR) and geometric (GSR) methods of super-resolution. The first class (OSR) – these are methods focused on the hardware implementation. While the second class (GSR) – these are methods, algorithmic implementation of which is based on the processing of similar images or their fragments sets. The idea of the geometric methods class of super-resolution – increasing of image or set of images on the basis of one or more samples of low resolution, for which pixel or sub-pixel shift is typical. When we talk about super resolution methods based on several samples of low resolution of one scene, the important point here is the presence of pixel or sub-pixel shift between them. It is the carrier of the additional information that will provide the opportunity to obtain image with high information content.

The rapid development of this class methods is characterized by the use of different tools to solve the set problem. Accordingly, developed a number of these methods classifications is developed [15], including the quantity of low resolution images, which are used in the work process [16] or concerning the area where these methods work [17], or concerning the actual method of the original sample reconstruction, and so on.

The most detailed classification of super-resolution methods, in our opinion, is provided in [18]. According to it, two methods groups of images super-resolution of the spatial domain are considered: a) classical - the methods which work with several samples of low resolution and b) on the basis of one image processing (Fig. 2). The authors in [18] define the following number of classical methods: methods of iterative back projection, iterative adaptive filtering, direct methods, methods based on the theory of projections on convex sets and probabilistic methods. It should be added that this classification is incomplete, since in recent years’ methods that combine various mathematical apparatus of the above mentioned groups and form a group of hybrid methods have developed [19, 20, 21, 22, 24].

Methods use of iterative back projecting [23] can cause such artifacts in the resulting image as effect of bell and aliasing. In addition, iterative process of error reconstruction minimization can converge to a few results. This causes the existence of multiple solutions; the algorithm may oscillate between them or converge to one of them.

Methods of iterative adaptive filtering are designed to handle video streams. Their main purpose is the unknown variables estimation that is why they mainly use a Kalman filter.

Methods group [25, 28, 27] on the basis of projections theory on convex sets is based on iterative finding of acceptable region element which is defined by the intersection of a number of convex constraints, starting from an arbitrary point. The main problem here is the definition of projections, which may occur as a not trivial task. In addition, there may be several solutions of these methods.

Another subgroup of methods [26] - statistical solves the problem of super - resolution stochastically by close to optimal image reconstruction. The resulting image, and underframes movement are treated as stochastic variables. These methods formulate the problem of super -resolution as an inverse problem, which is sensitive to a variety of artifacts. In addition, if the number of low-resolution images which are used by the method is less than the rate of resolution increase of the original image it is again reduced to incorrect problem. In other words, methods in this class also do not provide the uniqueness of the problem solution.

• III.    I MAGES P REPROCESSING

As in our previous work [2], input data of the developed method are two same resolution image:

I ¹ = [ c¹ 1 . j J i =1.. h     and    I ² = [ ^{c 2} i . j J i=1..h ^{,          (1)}

where c _i, j - the function of pixel intensity with coordinates ( i, j ).

The work proposed method requires preliminary processing on pairs of images, which determined execution following procedures.

• 1.    Normalization of images I 1 and I 2 according to the expressions:

  
  

  C . = C. . + — i , j           i , j

  
  

• 2.    Construction of the new vector c _i (using normalized input images (2)) from the corresponding lines (columns) using single-point crossover operation:

max c. . + min c. . г e[1; h ]; i, j г e[1; h ]; i’ j v j e[l; l]             j e[l; l]

c, j = Kc,, j ,                     (3)

Z                   X-1

where K = 1 max c. . I . As a result, we get: ( z e [ 1; h ] ; j e [ 1; l ] i , j )

V z e [ 1; h ] , j e [ 1; l ] : c, , _v >  0.

ci = ^^C 1 i ⁺ ( ^{1 -} k ) с 2 i ,               (4)

where k - crossover operations coefficient; c 1 i , c 2 i – dimension vectors l , elements of which are matrix rows I 1 and I 2 respectively. Use crossover operations to build new lines of image, shown in Fig. 1. The paper used the first case of variant b).

a) before crossover

b) after crossover

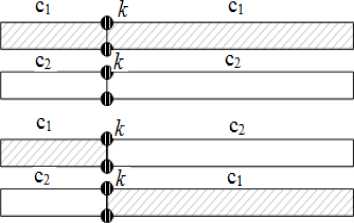
Fig.1. Using crossover operation for the synthesis of new line of image from two input

As a result, we obtain a new matrix:

I =▻.] , ., . ^ c- j       (5)

If the horizontal direction increase, matrix I will look like:

¹ =[ cj ] j = 1.. l                     ⁽⁶⁾

where c vectors constructed according to (4) for the corresponding columns normalized input images I 1 and I 2 respectively.

IV. D IVERGENCE M ATRIX C ONSTRUCTION

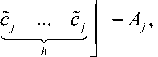
Aggregate divergence matrix V., that is the basis of the superresolution method, in the case of two input images, is constructed as follows [2]:

T

^{V i} e [ 1; h ] : ^V , = A, - ( c  ... c )    ,

A =----^:

max

c i ,1     ...     c i ,1

(ci,J\ c.   ... c

j cu = I £ ci, J V x=1

i , x

In applying the procedures for changing the resolution on rows of images I aggregate divergence matrix defined by (7) - (8) will look like:

T

V j e [ 1; l ] : V j =

^Aj =

max i h ] j 41 h ]

⁽ c J

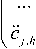
^cJi = 7

i

£ C x=1

V. D EFINING V ECTORS -F EATURES B ASED ON M OORE -P ENROUZE P SEUDOROTATION OF D IVERGENCE M ATRIX

The next step of the proposed method is to search vectors-features, which act as the image I characteristics of each line (column).

To solve the problem of characteristic vectors y_i building, which will perform as the characteristics of each line (or column) image C, we consider the equation:

Vy= Ci,(11)

where  ci ={с^j | j = 1.l} ; y =  (y,,i,  „., уц)  -l measurable vector of image С characteristic values for the i-th line.

In general, the characteristic vector y i (7) is defined as:

y=V-1 c,..(12)

Matrix V i is singular (det( V _i) = 0), so the inverse matrix V ^{- 1} does not exist. Therefore, to solve the problem (12) according to the theory on the minimization of the residual error ||x i - V _iy i || ² of the linear system [3] the following way of vector yi defining is proposed:

y = V + c , + (1 -V i +V , ) r , ,         (13)

where Vz+ - generalized inverse matrix Moore-Penrose (pseudorotation to Vi matrix [1, 3]); (1 -V.+V.) -projecting operator on the kernel Vi; ri - random vector of dimension l. The first term у (13) acts as pseudorotated solution, and the second is the solution of homogeneous s ys tem Viyi = 0. Provided through (13) method of defining vector characteristics of i-th element of overlapping x is possible as according to [3] matrix V+ Vz stoops to be бути inverse.

Moore-Penrose matrix V_z ⁺ is defined according to matrix singular distribution V i in the following way [3]:

V + = P i E + U T ,                 (14)

where U i , V i – unitary matrices of order l×l of matrix singular distribution V i; S + - matrix of order l*l, which is pseudorotated to the diagonal matrix S i of singular matrix distribution V _i . As matrix S i is also inverse, then matrix S ++ is received from S i by replacing all nonzero singular values о i,q ( ct_w >  s^ > ... >  оц >  0) to respectively conversed to them 1/ o i, q .

In the iteration process of finding according to yj+1 with (12) random vector r+1 was defined by residual error: r+1 = ||xi - Viy/\\i, where - l-norm

• VI. A UTOMATICALLY D ETERMINING THE C OEFFICIENT OF C ROSSOVER O PERATION IN TASKS D IGITAL I MAGES O VERSAMPLING

To develop the automated determination of k use approach to building optimization criterion based on a continuum of Syomkin similarity measures [5]:

KтА I , I ет ) =

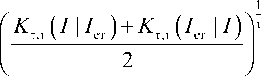
; - 1 < т < да , -да < i < да

where т - the measure of proximity of neighboring objects by Kolmogorov [6]; i e {+ да , 1, 0, 1, - да } -element of set plural ordered that defines one of the used similarity measures. For example, when т = 0, I = 1 we obtain the plural of Kulchynskiy K 0 _, 1 [7].

We proposed criteria feature of optimization task:

K e ( k ) = ^{1 f} E     K i ,Л k ) + K 1,-1 ( k ) 1 ,     (16)

• ⁶ ^ i е { -да,-1,0,1,+да }                                J

^{where K} 0,1 , ^K 0,0 , ^K 0, — 1 , ^K 0, — да , ^K 0, +да , K ₁, — ₁ ^{- Kulch} yn ^s ka appropriate plural [7], Otiai [8], Sorensen [9] Braun-Blanquet [10] Shymkevycha-Simpson [11, 12], Jacquard [13]. In the event of I ⁽²⁾ and reference the twice enlarged image I ^{( 2 )} these plurals as described in [13] at the fixed value of the coefficient k are written as follows:

,

К    I(2) /(2)  =      (          ет '   ■ К      /(2) /(2)=

K 0,0 ^{( 1}   , ¹ ет )      C77?27\Z77?2n ^;       K 0,^+да ' ¹   , ¹ ет )

(2^1(2)]

к h(2)т(2Л =______________(________ет-);

^{0,1 (     , ет} ) s ( I ^{( 2} ) ) +s ( I (2 ) ) - 2 S ( I ^{( 2} ) n 1 22 ) ) ^;

2 S ( I ^{( 2} ) n 1 22 ) )

_: ( 1 ² ) +s ( 1 2т ) -^( I ^{( 2 )}) -s ( 1 22 ) ) ^;

_n  и ( 2 )/( 24=   ^{2 S} ( ¹ ()^{n 1} ет ) ) .

^{0, - 1 (}     , ет ) s ( I и) +е ( 1 22 ) ) ^;

, ,     , _ s( i ⁽²⁾n42))           , ,     , _

К   (I ^{( 2 )} /^{( 2 )} I = —____________ - • к     (/^{( 2 )} /^{( 2 )} I =

1, ^{- 1 ( 1}    , ет ) _S ( I (2)_и I (2)) ^;    0 ' 1 ¹    , ¹ ет )

S ( I ^{( 2 )} ) + S ( I <² ) ) - 2 S ( I ^{( 2 )} n i £²⁾ ) + |s ( I ^{( 2 )} ) - S ( I 22 ) )|

s ( I ^mH( I S' ) + ^(^‘H I 2-1

,

where S - determine the dimension of the plural operator.

Choice of these coefficient for build criterial features

• (7)    conditioned by measures topological equivalence.

Then the optimization problem to select optimal values of crossover operation (opt( k )) can be written as:

opt ( k ) = arg

max k e [ 0,1 ]

K e( k ) .

It is worth paying attention that experimentally established that the optimization problem enough to solve just one of the stages consistent increase in the oversampling image task. The resulting value will be optimal or close to optimal in all the other stages of solving the task.

• VII. A LGORITHMIC I MPLEMENTATION OF M ETHOD

Solution of (12) with the operator of (7) or (10) is used to solve the problem of two-frame image superresolution in the case of crossover transactions. Since the input in this case there are two images І ₁ and І ₂, there are at least three solutions of the problem oversampling. The first two are similar to [1, 2] consists in the building enhanced images added to the original matrix and І 1 or І 2 vector с_i + y i position in line (or column). Here с i – the function of intensity of the input image (i.e., the original, not normalized by (2) and (3) of significance). A third solution is the synthesis of matrix rows and columns, enhanced by the expression:

c ,+ c, c ₃ ,.=--------+ y ,., i = 1.. l               (18)

SR increase procedure similar to the procedure described in [1, 2], consists of two consecutive parts, which oversampling image carried in the vertical and horizontal directions, respectively. Ordering action of each part of the algorithm can be arbitrary.

The algorithm for the image superresolution problem solving involves the following steps:

• 1)    construction mutated input vector from vectors corresponding two input images based on (4).

• 2)    construction aggregate divergence matrix (7) and (9).

• 3)    calculation of characteristic vectors y i square matrices built on relationships (7 or 9), on the iterative procedure (13).

• 4)    building enhanced image by adding to the original matrix I ₁ or I ₂ characteristic vectors like [2], or synthesis increased images according to (15).

The first three parts consistently applied to all the rows of I to increase the size of a given image height. Only then enlarged image matrix I ( m ) , I ( ^m ) or I ( ^m ) built by (15) or like according to [2].

Further procedure of increase implemented on larger image I ( 2 ) , I ( 2 ) or I ( 2 ) until the variable m reaches targeted coefficient increase.

• VIII.    R ESULTS OF P RACTICAL E XPERIMENTS

In order to assess the effectiveness of oversampling image by the developed method was conducted a series of practical experiments. A couple of input different qualities images, which used for simulation of the method shown in Fig.2. The crossover coefficient: k = 0.7. This value obtained by solving the optimization task used in the work to automatically determine k (Fig. 3.)

a)

Fig.2. A pair of input 2-byte, grayscale image, resolution, dimension - 231 x 199 pixels: a) I 1 ; b) I₂

b)

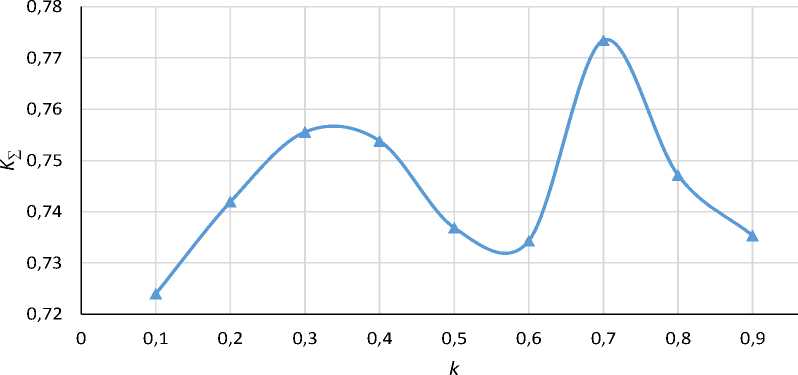
Fig.3. Dependence of the optimization criterion from values of operation crossover

• IX.    D ISCUSSION

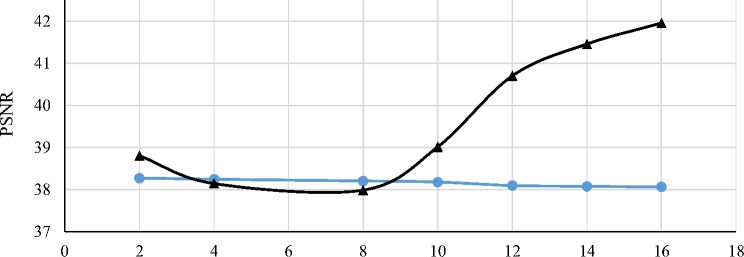
Fig. 4 shows PSNR depends, resulting oversampling of images 11,12 and the synthesis of image I(m) according to (15). As shown in Fig. 4 oversampling best results obtained at the synthesized image І(m). It is worth noting about PSNR behavior change. Three areas PSNR determine the intervals drop, growth and satiation values of PSNR (ie the growth with smaller gradient).

A significant increase PSNR in cases coefficient resolution change grater may be the main argument for practical using oversampling procedures, based on the proposed method.

Comparing the results of the proposed method and existing (in the case of one input image [1]) shows the following results (Fig.5).

0        2        4        6        8       10       12       14       16       18

Rate of increase resolution

• I1                     I2                     I

  Fig.4. Dependence PSNR from coefficient of increase for images I ( m ) , I ( m ) and I ( ^m ) obtained by method

  

  Rate of increase resolution, m

  existing method                           developed method

  
  

Fig.5. Comparison of the work developed and existing methods based on PSNR when changing m

From the Fig. 4 we can say that for small coefficient values of increase (m <10) using the proposed method is not justified since PSNR values for existing methods are considerably higher. The value of PSNR developed method starting to exceed the value of PSNR for existing only when m> 10. Obviously, the exact value of the inflection point m = 10 in the comparison of the effectiveness of the methods obtained for a given image І ₁ and І ₂ . However, experiments with other images in general, confirmed that for other images this point will be close to exactly value of 10.