Имитационная дискретно-событийная стохастическая модель процесса разработки и согласования конструкторско-технологической документации на авиастроительном предприятии
Автор: Полянсков Юрий Вячеславович, Бутов Александр Александрович, Железнов Олег Владимирович
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Статья в выпуске: 1-5 т.16, 2014 года.
Бесплатный доступ
Проведен анализ процесса разработки и согласования конструкторско-технологической документации в рамках бизнес-процесса конструкторско-технологической подготовки производства авиастроительного предприятия, сформулирована его математическая модель в терминах системы массового обслуживания и разработана имитационная модель с модифицированным алгоритмом оптимизации OptQuest в программной среде AnyLogic.
Имитационная модель, управление потоками работ, распределенная эволюционная сеть, многокритериальная оптимизационная задача
Короткий адрес: https://sciup.org/148205690
IDR: 148205690 | УДК: 004.942
Текст научной статьи Имитационная дискретно-событийная стохастическая модель процесса разработки и согласования конструкторско-технологической документации на авиастроительном предприятии
Создание сложной наукоёмкой продукции требует координации разнообразных процессов, и задержка на одном участке ведет к срыву сроков на других. Удлинение полного цикла проектирования и производства продукции, включающего предпроектные исследования, конструкторско-технологическую подготовку производства (КТПП), материально-техническое снабжение, собственно производство, негативно сказывается на положении предприятия как вследствие потери гибкости и конкурентоспособности, невыполнения требований заказчиков, так и в результате снижения экономической эффективности. В связи с этим необходимо выявление и устранение основных причин, определяющих увеличение длительности производственного цикла.
Проведено исследование относительной частоты возникновения задержки изготовления нового воздушного судна вследствие различных факторов. Результаты анализа показали, что в 63% всех случаев причиной является несвоевременный запуск в производство конструкторско-технологической документации (КТД). Этап разработки и согласования КТД является одной из наиболее продолжительных и затратных стадий полного цикла создания новой продукции и
составляет 25-35% трудоемкости. Процесс управления разработкой и согласованием КТД оказывает существенное влияние на продолжительность производственного цикла изделия. Процесс управления подразумевает функции планирования, распределения и контроля над выполнением рассматриваемого процесса.
Начиная с 70-х годов прошлого века основой систем автоматизированного управления производством послужили задачи оптимизации [1], в первую очередь теория расписаний, получившая развитие, начиная с работ Конвея и Максвелла [2]. В связи с выявленными трудностями решения NP-полных задач были разработаны квазиоптимальные методы решения подобных задач, среди которых генетические алгоритмы, нейронные сети, метод отжига, алгоритм «муравьиных колоний» и др. [3].
Цель работы: разработка математической модели оценки достаточности ресурсов процесса разработки и согласования КТД в рамках бизнес-процесса КТПП авиастроительного предприятия.
С математической точки зрения это задача определения плановых сроков и их сдвигов, а также распределения работ, то есть составления расписания. Составление расписаний, в особенности на оперативном уровне, является одной из наиболее сложных задач, поскольку размерность задачи значительна, количество возмущающих случайных факторов очень велико, а многие из них не поддаются учёту. Для труда конструкторов и технологов рассмотренная ситуация осложняется тем, что творческая деятельность в меньшей степени планируется и нормируется, что вызывает проблемы с её формализованным описанием. Поставлена задача разработки имитационной дискретно-событийной стохастической модели процесса разработки и согласования КТД в терминах систем массового обслуживания (СМО). Важной задачей над имитационной моделью является выполнение оптимизационного эксперимента, в результате которого находятся Парето-оптимальные решения целевой функции математической модели.
Математическая модель оценки достаточности ресурсов процесса разработки и согласования КТД. Процесс разработки и согласования КТД представляет собой строгую последовательность определенных действий УГК и УГТ согласно действующим ГОСТам, СТП предприятия и план-графику. Основная IDEF0 схема процесса разработки и согласования КТД представлена на рис. 1. На вход процесса поступают чертежи детали (сборочной единицы), электронная модель детали, информация об изменениях КД. В ходе процесса разрабатывается следующая КТД: технологическая инструкция, маршрутная карта, карта технологического процесса, операционная карта, комплектовочная карта, ведомость подготовки производства, ведомость плазово-шаблонной оснастки.
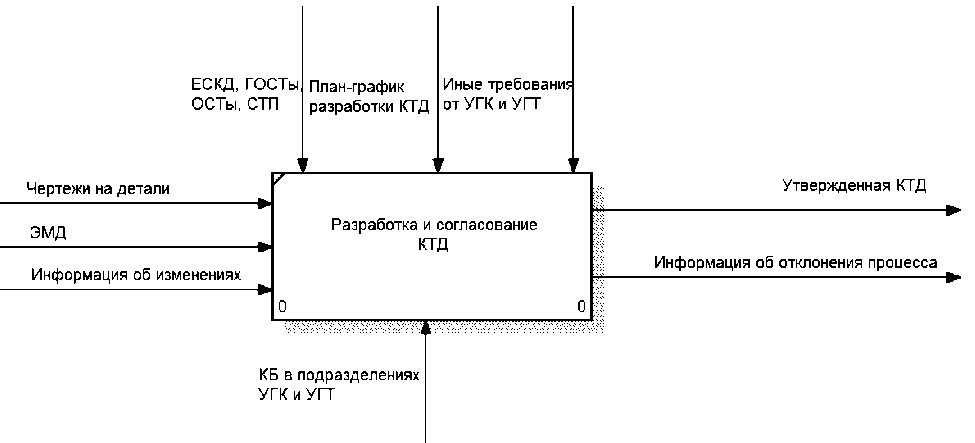
Рис. 1. Схема процесса разработки и согласования КТД
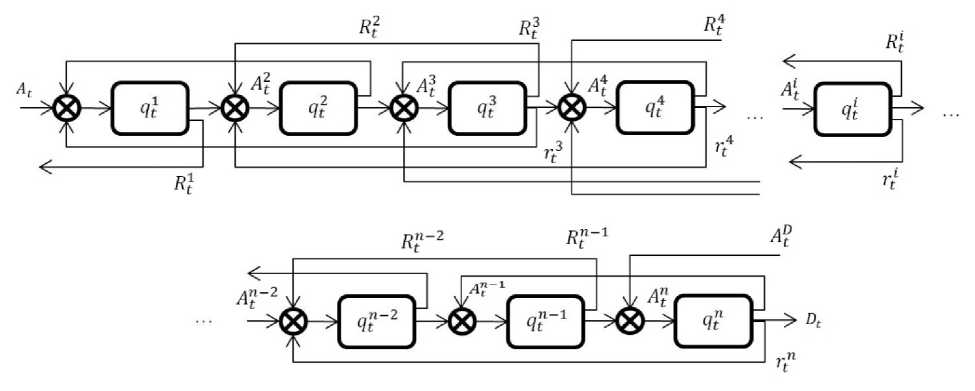
Рис. 2. Схема СМО для процесса разработки и согласования КТД
Пусть есть некий объем КД, который поступает из внешнего конструкторского бюро в отдел УГК авиастроительного предприятия. При выполнении бизнес-процесса КТПП данный объем КД прорабатывается и в результате разрабатывается конструкторско-технологическая документация для изготовления детали на самолет. Наша задача состоит в том, чтобы в режиме реального времени проводить мониторинг, анализ и управление процессом разработки и согласования КТД, сравнивать значения управляемых показателей с найденными оптимальными значениями и находить «узкие места» процесса для управления (отделы КТПП по вине которых произошли отклонения фактических от планируемых показателей). Приведено формальное математическое описание модели для процесса «Разработка и согласование КТД» [4]. Рассмотрим данный бизнес-процесс в виде схемы узлов системы массового обслуживания (рис. 2).
Считаем, что комплект КТД состоит из конечного числа документов и электронных моделей деталей, тогда считающий процесс числа единиц поступившей КД в i -й отдел КТПП будет иметь вид:
Л- = (^„ о (1)
Считающий процесс числа единиц обрабатываемой КТД в i- м отделе КТПП будет иметь вид:
«' = to™(2)
Считающий процесс числа единиц полностью проработанной КТД в i-м отделе КТПП будет иметь вид:
D- = №„_„(3)
Считающий процесс числа возвращаемой на доработку КТД из i- го в i-1 отдел будет иметь вид:
R- = (Ri)tM
Считающий процесс числа возвращаемой на доработку КТД из i- го в i-2 отдел будет иметь вид:
r- = (Г/Хы
Для балансовых соотношений составлены уравнения считающего процесса числа поступившей и количество обрабатываемой КТД в i -м отделе.
X + (1 - т-^ • a2 • M2 + (1 - ^ • a3 • M3 -
-
— (1 -Tj^. a^-(1 - ТГ ) )-^ = 0
(1 - ТГ . у a^ + (1 -Tj j -y r 3 + (1 -T^y r < -
-
- (1 - Т Т 2- ) • a2 • M2 - (1 - Т Т 2- ) • R2 = 0
(1 - Т Т - ) ) • a--1 • M--1 + (1 - Т - Т— ) • R-+1 + (1 - —Т- - ) - r-+ 2 -
-(1 -)• a - • M - - (1 - TT ^ - )•R - -(1 - ТТ ) )т - = 0
Считаем, что интенсивность поступления КД от внешнего КБ имеет распределение по закону Пуассона с функцией распределения времён между моментами поступления документации F(t) = 1 - e-Xt. Оптимизационная задача формулируется следующим образом: необходимо определить количество сотрудников с учетом должностных (функциональных) ролей, обеспечивающих наилучшую динамику выпуска КТД с учетом минимизации двух целевых критериев: объема возвращаемой на доработку КТД и затрат на оплату труда сотрудникам КТПП, тогда целевая функция Ф1 математической модели будет иметь вид:
Ф^М1.....М ^ ) = {(1 - Т-) • a " • M ^ } - {Z P=1 Т- • M-} • Л ^ maxn i nn Dt- (7)
при условии, что M1 + M2 + ... + Mn = M, при Л ^ 1, где Т(п) - время простоя n-го отдела; T -общее время эксперимента; Mn - количество сотрудников в n-м отделе; Т- - время на проработку i-го комплекта КТД; an - коэффициент пропорциональности количества проработанной КТД и числа сотрудников n-го отдела.
Для проверки адекватности разработанной математической модели оценки достаточности ресурсов бизнес-процесса разработки и согласования КТД и проведения оптимизационных экспериментов ее целевой функции построена имитационная модель в виде дискретнособытийной стохастической модели многофазной СМО с использованием программного продукта AnyLogic.
Имитационная модель процесса разработки и согласования КТД. С использованием встроенного функционала AnyLogic разработана имитационная модель процесса разработки и согласования КТД в виде дискретно-событийной стохастической модели. В модели заданы узлы в виде отделов КТПП, вероятностные переходы и связи между узлами (рис. 3).
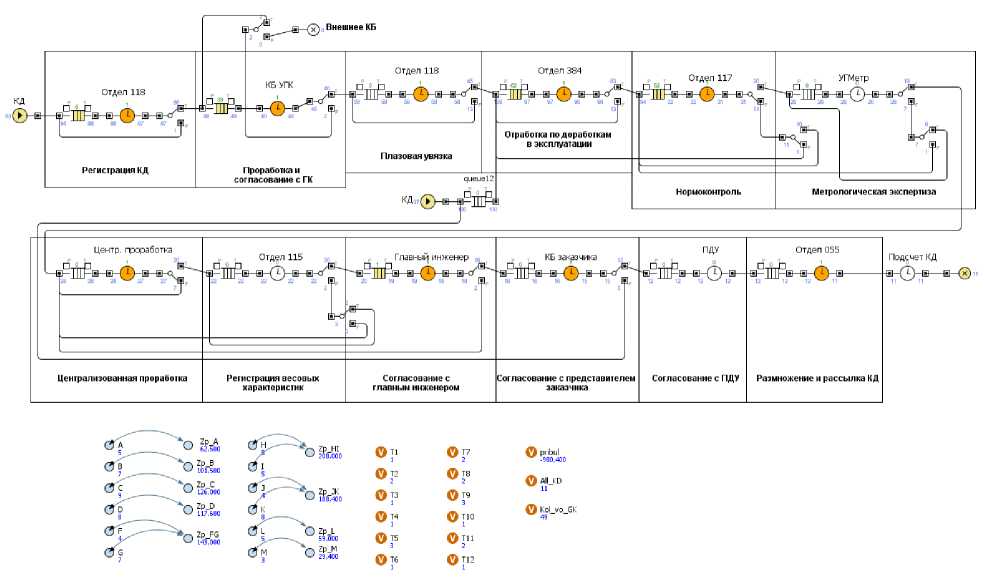
Рис. 3. Имитационная модель процесса разработки и согласования КТД
На имитационную модель накладываются следующие ограничения:
-
- номенклатура включает 4 вида изделий;
-
- 12 отделов КТПП по разработке КТД;
-
- 280 сотрудников;
-
- 12 должностных (функциональных) ролей для сотрудников;
-
- 2 CAD/CAM/CAE системы;
-
- работа строится в 2 смены;
-
- ведется разработка и согласование 11 видов КТД;
-
- 2 вида производства (единичное и серийное).
Важно отметить, что взаимосвязь между основными объектами модели является «многие-ко-многим» - другими словами, для разработки одного вида КТД (например, электронной технологической модели) может использоваться несколько видов CAD/CAM/CAE систем и одна CAD/CAM/CAE система может быть использована для нескольких видов КТД. В результате переменные рассматриваемой модели являются многомерными, что порождает многомерное пространство поиска решений и повышает вычислительную сложность оптимизационной задачи. В результате строится граница Парето, которую образуют недоминируемые Парето-решения. Другими словами, остальные решения не позволят добиться одновременно более низких значений объема возвращаемой на доработку КТД и затрат на оплату труда сотрудникам КТПП. Следует отметить, что все слагаемые в формуле целевой функции имеют связь между собой, установленную через отношения внутри модели. Так, например, заложенные функции спроса, издержек и производства позволяют найти оптимальный баланс между планом выпуска КТД и планом разработки с учетом производственных ограничений.
Так как целевая функция порождает многомерное пространство поиска решений, вычислительная сложность оптимизационной задачи становится преградой к ее решению за допустимое время. Встроенного функционала в AnyLogic недостаточно для решения поставленной оптимизационной задачи, поэтому рассматриваемая имитационная модель была интегрирована с разработанной распределенной эволюционной сетью с использованием технологии Intel-liJ IDEA на языке программирования Java. В результате, формирование фронта Парето заняло всего 2 минуты. При этом каждый из вычислительных процессов произвел 670 итераций вычисления целевой функции рассматриваемой имитационной модели. Таким образом, система обеспечила решение поставленной многокритериальной задачи за допустимое время.
Выводы: описан процесс разработки и согласования КТД КТПП авиастроительного предприятия, разработана математическая модель оценки достаточности ресурсов для планового функционирования рассматриваемого процесса. Разработана имитационная модель процесса разработки и согласования КТД с использованием программного продукта AnyLogic в виде дискретно-событийной стохастической модели. Предложен и реализован подход к решению многокритериальных оптимизационных задач большой размерности на основе алгоритма OptQuest в программном продукте AnyLogic. Разработана программа на языке программирования Java, интегрированная в имитационную модель AnyLogic.
Работа выполнена в рамках государственного задания Минобрнауки России.
Список литературы Имитационная дискретно-событийная стохастическая модель процесса разработки и согласования конструкторско-технологической документации на авиастроительном предприятии
- Моисеев, И.Н. Математика ставит эксперимент. М., Наука, 1975. 226 с.
- Конвей, Р.В. Теория расписаний/Р.В. Конвей, В.Л. Максвелл, Л.В. Миллер. -М., Наука, 1975. 359 с.
- Goldberg, D.E. Genetic algorithms in search, optimization, and machine learning. -Addison-Wesley, Reading, MA, 1989. Дата обращения: 30.08.2014 http://www.amazon.com/Genetic-Algorithms-Optimization-Machine-Learning/dp/0201157675
- Железнов, О.В. Численные расчеты по математической модели оценивания вероятности возникновения сбоя функционирования бизнес-процесса КТПП авиастроительного предприятия/О.В. Железнов, Ю.В. Полянсков/Известия Самарского научного центра РАН. Т. 15, 2013. № 4(4). С. 854-859.


