Имитационная компьютерная модель для виртуальных исследований измерительных оптико-электронных систем

Введение. Задача дистанционного определения пространственного положения различных стационарных и динамических объектов эффективно решается с использованием оптикоэлектронных измерительных систем. В настоящее время в качестве основного детектирующего элемента, в плоскости которого строится изображение измеряемого объекта, является фотоприемная матрица (ФПМ) [1]. Координаторы на основе ФПМ используются при астрономических и геодезических измерениях, в приборах наведения и прицеливания [2; 3], системах идентификации личности по биометрическим параметрам [4]. В последнем случае речь идет о регистрации координат некоторых кардинальных точек, соотношение расстояний между которыми является одним из компонентов вектора идентификации.

За базовый измеряемый элемент целесообразно принять изображение точечного объекта. Именно погрешность измерения координат этого элемента определяет функциональное качество прибора. Очевидно, что в случае идеальной оптической системы, изображением точки будет являться точка. Тогда погрешность измерения определяется геометрическими размерами отдельного чувствительного элемента матрицы (пикселя) [5]. Снижение погрешности возможно за счет того, что реальный объектив создает изображение точки в виде пятна рассеяния.

При формировании такого пятна энергия изображения уже не концентрируется на одном чувствительном элементе матрицы, а распределяется по поверхностям нескольких детекторов, что создает зарядовый рельеф в области накопления сигнальных зарядов ФПМ. Получив точные числовые значения сигналов для смежных элементов, на которые проецируется пятно рассеяния, и обработав эти значения с помощью интерполяционного алгоритма, учитывающего дисбаланс распределения сигналов по элементарным детекторам, можно рассчитать координаты центра пятна по вертикали и горизонтали ФПМ относительно заданного центра координат в плоскости ФПМ.

Если пятно рассеяния является круглым, что характерно для его нахождения в центральной (параксиальной) зоне поля зрения, то нет необходимости проводить интерполяционную обработку по всем элементам матрицы, попавшим в зону энергетического воздействия оптического сигнала. Достаточно определить экстремальный пиксель с максимальным сигналом и построить интерполирующие функции только по вертикальному и горизонтальному наборам детекторов, симметричных относительно экстремального элемента (по столбцу и строке, соответственно).

Если ФПМ является идеальной, то есть в ней отсутствуют шумы и темновые токи, то погрешности расчета горизонтальной или вертикальной координаты будут уменьшаться при увеличении количества элементов выборки до некоторого значения, обеспечивающего репрезентативность результата. Дальнейшее увеличение числа обрабатываемых пикселей уже не будет влиять на погрешность. Сама же погрешность в этом случае будет определяться вычислительной погрешностью компьютера.

Для реальных ФПМ характерно наличие как темновых токов, так и шумов. Это приводит к деформации идеального зарядового рельефа и увеличению погрешности измерения координат [6], причем увеличение количества обрабатываемых пикселей может увеличить погрешность измерения, поскольку в обработку будут включены элементы, в которых сигнальные заряды уже отсутствуют, а шумовые компоненты продолжают участвовать в процессе вычисления. На результирующую погрешность оказывают влияние и другие факторы, такие как нестабильность исходного оптического сигнала, турбулентность атмосферы, вибрации и т. п. Можно сказать, что погрешность измерения определяется флуктуациями сигнала, распределенными по оптико-электронному тракту и имеющими различное физическое происхождение [7].

Постановка задачи. В настоящее время уменьшение погрешности измерений достигается в основном за счет улучшения качественных показателей аппаратной части приборов и усовершенствования алгоритмов обработки выходных сигналов ФПМ [8]. Компьютерное моделирование применяется, как правило, для предварительной отработки тех или иных проектных решений на стадии научно-исследовательских работ [9].

Наличие компьютерной модели, позволяющей осуществлять оптимальное согласование звеньев координатора по критерию минимизации погрешности измерений, является актуальной задачей, решение которой обеспечит адаптацию проектируемого или эксплуатируемого измерительного прибора к реальным условиям его применения с целью повышения точности измерений.

Как было отмечено выше, основными факторами увеличения погрешностей измерений являются флуктуационные (шумовые) процессы, распределенные по оптико-электронному тракту. Наличие случайных составляющих в полезном сигнале требует реализации основного алгоритма моделирования в формате многократных статистических испытаний. В этом случае параметры и характеристики звеньев прибора первоначально задаются в виде номинальных значений, имеющих суть математического ожидания для каждого компонента, участвующего в вычислительном процессе. Также для этих компонентов определяется вероятностный закон, описывающий поведение случайной величины, и необходимые для моделирования параметры случайного процесса, например, среднеквадратическое отклонение (СКО).

При однократном компьютерном эксперименте в плоскости ФПМ генерируется случайная точка (ее координаты). Затем, в соответствии с законом распределения энергии в пятне рассеяния, строится соответствующая пространственная функция с вершиной, координаты которой соответствуют координатам сгенерированной точки. С помощью операции свертки между растром матрицы и функцией распределения энергии рассчитывается распределение сигнальных зарядов матрицы, которые затем преобразуются, с учетом вероятностного характера физических процессов, в случайную дискретную функцию сигналов, накапливаемых пикселями ФПМ. По этой дискретной функции методом интерполяции рассчитывается приблизительное значение центра пятна рассеяния. Разница между положением истинной случайной точки и рассчитанного центра пятна запоминается в качестве однократной случайной погрешности.

Проведение серии многократных статистических испытаний при каждом новом случайном положении сгенерированной точки и уникальном распределении случайных параметров матрицы позволяет в итоге получить СКО для всей совокупности статистических экспериментов. Каждая новая серия статистических экспериментов предполагает целенаправленное детерминированное изменение одного из контролируемых параметров координатора в реальном диапазоне допустимых значений. Таким образом, реализуется функция зависимости погрешности измерения координат 5 i от изменяемого параметра p i , то есть 5 i = f( p i ). Минимальное значение этой целевой функции и будет являться оптимальным значением параметра, обеспечивающим наименьшую погрешность измерения при прочих равных условиях.

Очевидно, что проведение подобного анализа в многопараметрическом пространстве позволит получить оптимально согласованный набор контролируемых параметров, отвечающий критерию минимизации погрешности измерений. Необходимо отметить, что решение поставленной задачи не предполагает разработки новых приборов или методов измерения координат, а также не затрагивает вопросы совершенствования алгоритмов определения положения вершины функции распределения энергии в пятне рассеяния. Основной целью исследования является разработка компьютерно-ориентированных средств и методов оптимального согласования контролируемых проектировщиком или оператором параметров и характеристик звеньев оптико -электронного тракта измерительного прибора, которое бы обеспечивало минимизацию погрешности измерения при наличии уже заданного (проектируемого или физически реализованного) координатора. То есть речь идет о создании виртуального испытательного стенда для оптимального выбора параметров и режимов работы планируемого к практическому использованию реального прибора с учетом реальных условий его работы в соответствии с заданным функциональным назначением.

Как уже было отмечено выше, пятно рассеяния, формируемое в параксиальной области, является круглым. Инвариантность такого пятна относительно выбранной системы координат позволяет задать функцию распределения освещенности в пятне Е(х, у) только для одной координаты. Пусть такой координатой является x . Сама функция предполагается гауссовой:

⁽ x — x 0 )

E(x) = • e 2nr2 , (1) 2 • п r где Фо - мощность падающего излучения; xо - реальная случайная координата точки, сгенерированной в плоскости ФПМ; r - радиус пятна рассеяния на уровне 0,606 от максимального уровня освещенности.

При однократной генерации флуктуаций учитываются только шумы ФПМ, которые задаются в долях от полезного сигнала для мультипликативной шумовой составляющей и аналогично в долях от темнового сигнала для аддитивной шумовой составляющей.

Свертка матричного растра и функции распределения освещенности в изображении точки приводит к преобразованию непрерывного входного оптического сигнала E(x) в ступенчатую дискретную функцию S(i) , где S - электрический сигнал, а i - номер элемента растра матрицы по строке. Каждый элемент вектора S(i) содержит в себе детерминированный для конкретной случайной реализации точки сигнал, определяемый интегральной освещенностью i -го элемента растра, и шумовую случайную составляющую, генерируемую внутри i -го элемента в соответствии с заданным СКО. Для определения координаты центра x ц пятна рассеяния использовался простейший интерполяционный алгоритм расчета энергетического центра, являющийся модификацией известного из курса теоретической механики метода определения центра масс системы материальных точек:

2 m =i S ( i ) - Х ц ( i )

,

Х =------—

ц      x, m S ( i )

где S(i) – сигнал в i -том элементе строки; x ц (i) – координата центра i -того элемента; m – количество элементов выборки, участвующих в обработке.

Расчет окончательной погрешности проводится по совокупности всех случайных реализаций для конкретной серии многократных статистических испытаний.

Обсуждение результатов моделирования. Очевидно, что если размер пятна рассеяния меньше размеров пикселя, то погрешность измерения координаты центра пятна будет определяться размерами пикселя. Увеличение диаметра пятна рассеяния приведет к уменьшению погрешности за счет включения в процесс обработки смежных пикселей. Слишком большое «расширение» пятна снизит энергетический уровень оптического сигнала за счет распределения энергии по большей площади. Следовательно, должен существовать некоторый оптимальный радиус пятна, который обеспечит минимальную погрешность измерений. Проверке этой гипотезы были посвящены работы [10; 11]. При заданных параметрах растра и значений шумовых компонент был проведен виртуальный эксперимент, в котором радиус пятна рассеяния менялся с определенным шагом от значения размера пикселя до размера в несколько сотен пикселей. При каждом новом значении радиуса проводились многократные статистические испытания и рассчитывалась текущая погрешность. На рис. 1 показан результирующий оптимизационный график, из которого видно, что действительно существует радиус пятна рассеяния, обеспечивающий минимизацию погрешности измерения.

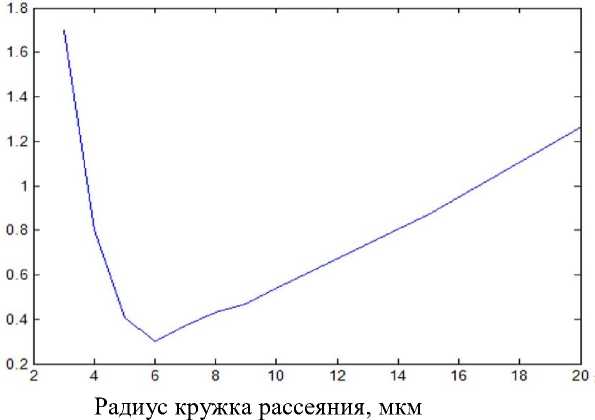
Рис. 1. Зависимость оптимальной погрешности измерения координаты от радиуса пятна рассеяния Fig. 1. Dependence of the optimal coordinate measurement error on the scattering spot radius

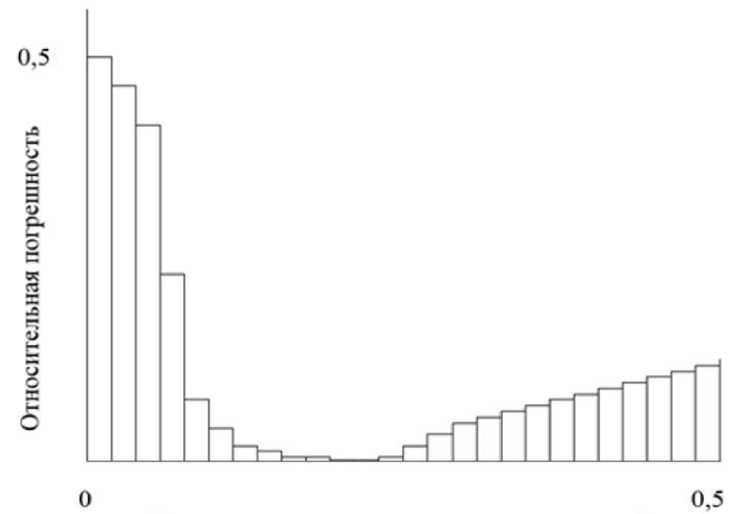
Также определялось оптимальное количество элементов выборки, обеспечивающее минимизацию погрешности [12]. Число пикселей, участвующих в интерполяционном процессе дискретно увеличивалось от 1 (пиксель с максимальным сигналом) до n (общее количество пикселей в строке). Приращение пикселей производилось симметрично в обе стороны от экстремального пикселя. Каждый шаг сопровождался расчетом погрешности методом многократных статистических испытаний. При малом количестве элементов выборки погрешность имела большую величину. Затем, по мере увеличения участвующих в обработке пикселей, погрешность снижалась. Но с определенного значения обрабатываемых пикселей она опять начинала возрастать. Это связано с тем, что на периферии пятна полезный сигнал становился меньше шумовых сигналов, которые начинали вносить весомый вклад в конечную погрешность, причем тем больший, чем больше «шумовых» пикселей, не содержащих сигнальных составляющих, добавлялось в процесс обработки. На рис. 2 приведен ступенчатый график, иллюстрирующий результаты описанного вычислительного эксперимента.

Нормированное количество элементов выборки

Рис. 2. Зависимость относительной погрешности измерения координаты от количества элементов выборки

Fig. 2. The dependence of the relative error of coordinate measurement on the number of sample elements

Для данного графика по горизонтали откладывалось нормализованное относительно общего количества пикселей в строке число пикселей выборки, а по вертикали – погрешность измерения.

Графики, приведенные на рис. 1 и 2, носят иллюстративный (показательный) характер, а параметры матриц в вычислительных экспериментах подобраны таким образом, чтобы повысить наглядность представляемых результатов. В этой связи нет необходимости приводить параметры оптико-электронных трактов измерительных систем, для которых эти графики были получены.

Представляет интерес внешний вид экранных интерфейсов, на которых представлены результаты однократных статистических испытаний. Данные изображения приведены на рис. 3 и 4.

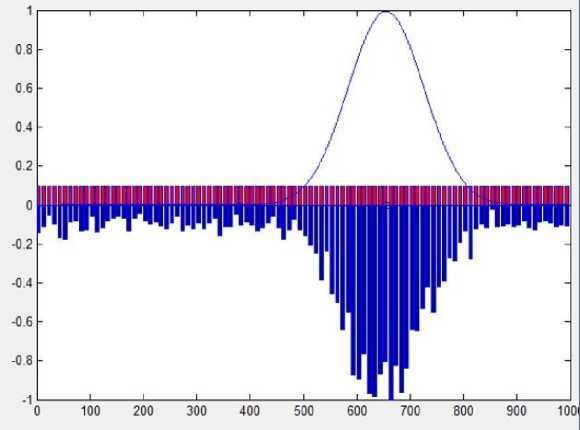
Рис. 3. Распределение зарядовых пакетов по пикселям строки матрицы при малом радиусе пятна рассеяния

Fig. 3. Distribution of charge packets over the pixels of the matrix row at a small radius of the scattering spot

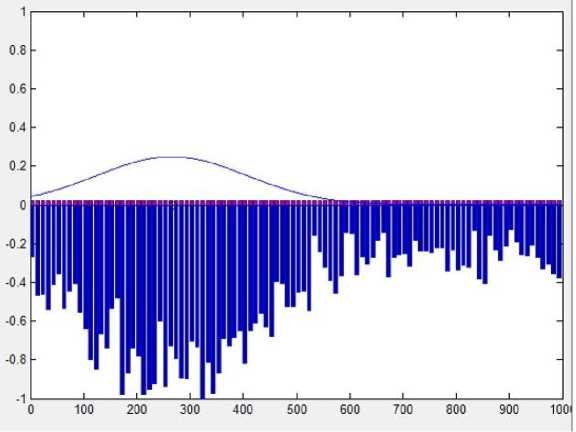
Рис. 4. Распределение зарядовых пакетов по пикселям строки матрицы при большом радиусе пятна рассеяния

Fig. 4. Distribution of charge packets over the pixels of the matrix row at a large radius of the scattering spot

В верхней части рис. 3 и 4 отображается гауссова функция распределения освещенности в пятне рассеяния. Нижняя часть соответствует дискретному распределению зарядов (сигнальных и шумовых), накопленных под воздействием оптического излучения. Очевидно, что на рис. 3 за счет меньшего размера пятна рассеяния зарядовый рельеф имеет более четкий характер. А увеличение радиуса пятна на рис. 4 приводит к «расплыванию» зарядового рельефа. В обоих случаях количество энергии пятен остается постоянным, но увеличение радиуса на рис. 4 уменьшает долю энергии, приходящейся на 1 пиксель. Поэтому зарядовый рельеф, изображенный на рис. 4, претерпевает заметные деформации, что, конечно, приводит к значительному возрастанию погрешности измерения центра пятна рассеяния.

При анализе динамичного объекта [13], например, с целью определения как траектории его движения, так и параметров, характеризующих перемещение объекта (скорость, ускорение), производится последовательная серия измерений координат его текущего положения через равные промежутки времени, определяемые периодом накопления сигнала. Очевидно, что уменьшение времени накопления привело бы к более точным измерениям, но при этом сигнальный заряд не будет успевать накапливаться до величины, необходимой для точной фиксации расчётной координаты. В то же время увеличение времени накопления приведет к размытию изображения [14; 15]. Возникает задача определения такого оптимального времени накопления, которое бы обеспечивало наименьшую погрешность измерения текущей координаты. Подобная задача также могла бы быть решена с помощью предлагаемой модели.

Заключение. Описанная модель имеет обобщенный характер и лишь демонстрирует некоторые возможности, предоставляемые ею с точки зрения оптимального согласования отдельных параметров и режимов работы оптико-электронных измерительных систем. Развитие модели происходит, во-первых, по пути конкретизации применительно к реальным проектируемым или эксплуатируемым приборам, а во-вторых, в направлении развития многопараметрической оптимизации координаторов за счет объединения в один моделирующий процесс параметров и характеристик различных звеньев системы.

Все это создает предпосылки для создания виртуального стенда, обеспечивающего разработку и настройку измерительных систем, наиболее эффективно выполняющих планируемые для них задачи.