Имитационная модель рабочего процесса манипулятора при удалении нежелательной растительности вместе с корневой системой в лесных насаждениях

Одним из приёмов выращивания полноценных и долговременных лесных культур [1], [2] является осветление, в процессе которого регулируют густоту и улучшают условия роста деревьев главной породы. Осветление проводят в насаждениях, начиная с 3…5 и до 10 лет, а при зарастании междурядий порослью второстепенных лиственных пород необходимость осветления культур появляется уже на втором году после посадки. Особенно это характерно для зоны смешанных лесов, где обилие тепла, плодородные почвы и достаточное количество осадков приводят к массовому появлению поросли осины и берёзы. Поэтому, если своевременно не проводить осветление, то, как отмечают многие учёные [3], [4], лесные культуры гибнут.

Для срезания поросли могут применяться кусторезы ручные и тракторные с пассивными и активными рабочими органами [5]. В частности, определённое применение находят кусторезы с рабочими органами активного действия [6—8] фрезерного типа, к которым относятся тракторные кусторезы КОГ-2.3, КОМ-2.3, КОН-2.3, КО-1.5 и др. Однако после срезания этими (а также иными) кусторезами поросль продолжает развиваться, что снижает сроки очередного проведения осветления. Поскольку поросль разнообразна по своим параметрам (диаметр, высота) и физико-механическим свойствам (сопротивление изгибу, жёсткость стволика), то доля уничтожаемой поросли составляет всего лишь 30…40 %. В соответствии с этим нам представляется актуальным проведение дополнительных исследований, направленных на устранение имеющихся недостатков в существующих способах и средствах удаления нежелательной растительности.

2.    Материалы и методы

Одним из способов уничтожения нежелательной растительности, обеспечивающим невозобновление её произрастания на очищаемой территории, является способ удаления нежелательной поросли вместе с корневой системой [9] и переработкой в щепу каждого удаляемого экземпляра древесно-кустарниковой растительности. Подобные воздействия на нежелательную поросль способствуют уменьшению ручного труда работников лесных предприятий, сокращению затрат на вывоз и последующую утилизацию порубочных остатков, уменьшению (вплоть до полного исключения) необходимости повторной обработки ранее очищенных площадей и, в целом, повышению качества осветления лесных культур.

В соответствии с указанным способом воздействие на нежелательную поросль осуществляется рабочим органом, закреплённым, например, на конце стрелы манипулятора (рисунок 1) многофункционального транспортного средства. Рассматриваемый в данной работе манипулятор представляет собой платформу 1 с поворотными стойкой 2 и корпусом 3, внутри него возвратно-поступательно перемещается шток 4. На конце штока установлено рабочее оборудование 5 (в данном случае — клещевой захват).

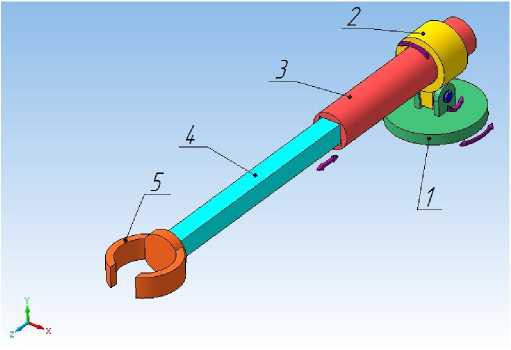
Рисунок 1. Малозвенный манипулятор с рабочим оборудованием

Figure 1. Manipulator with a small number of links and working equipment

Отметим, что на современном этапе развития науки и техники одним из основных этапов разработки наукоёмкой продукции является моделирование сложных систем или процессов [10], [11], поскольку современная технология является чрезвычайно сложным техническим объектом. В целом вопросами моделирования работы машин с манипуляторными установками занимался целый ряд как отечественных (например, [12—15]), так и зарубежных [16—18] учёных, однако нами было выявлено недостаточное изучение вопроса моделирования рабочего процесса малозвенного манипулятора с закреплённым на конце его стрелы рабочим органом. С учётом полученных нами результатов по моделированию сферического рабочего пространства машин с манипуляторными установками [19] для определения оптимальных значений конструктивных и технологических параметров рассматриваемого в данной работе манипулятора с размещённым на его конце рабочим органом необходимо разработать математическую модель процесса воздействия указанных технических средств на нежелательную поросль, обеспечивающего высокие характеристики производительности и качества работы как самого манипулятора, так и рабочего органа [20], [21]. Выполненное в данном исследовании моделирование было основано, в целом, на методах классической механики [22—24].

3.    Результаты

Для обоснования кинематических и динамических параметров манипулятора нами была разработана математическая модель рабочего процесса удаления нежелательной поросли с его корневой системой. На рисунке 2 приведена расчётная схема манипулятора для определения его кинематических параметров.

Характерными точками на данной схеме являются точки A и B — точки, связанные с удаляемой нежелательной порослью, при этом в качестве точки A нами был принят верх основного ствола нежелательной растительности, а в качестве точки B — начало её корневой системы.

Рассматриваем координаты крайних точек A и B выдернутой с корнем поросли в системе координат при повороте растительности на угол (рисунок 3).

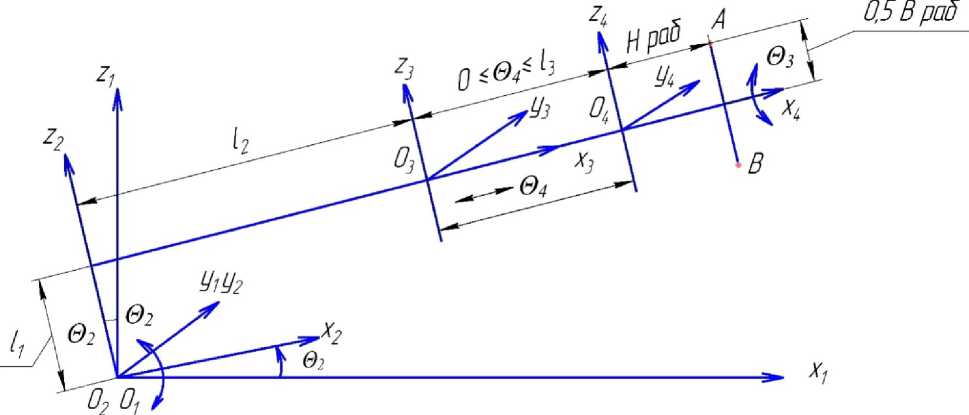
Рисунок 2. Расчётная схема манипулятора для определения кинематических параметров

• Figure 2.    Design diagram of the manipulator for determining the kinematic parameters

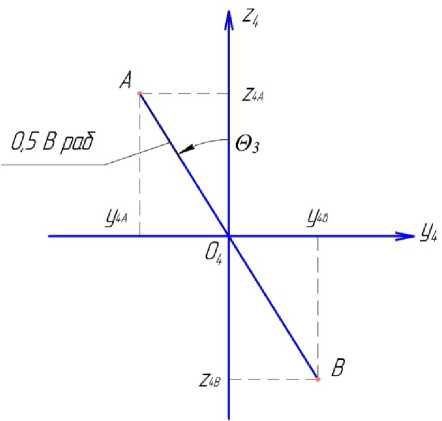
Рисунок 3. Положение выдернутой поросли в системе координат ZOY

• Figure 3.    The position of the pulled out underwood in the ZOY coordinate system

При этом положительное направление вращения © 3 принимаем против часовой стрелки со стороны положительного направления оси x 4 ( го д >  0):

X 4A = H раб = Н	X b = Н
< Y 4 a = - 0,5 • B • sin © 3	Y 4 В = 0,5 • B • sin © 3	(1)
_ Z 4 A = 0,5 • B • cos © 3	Z 4 В =- 0,5 • B • cos © 3

При переносе начала координат из точки О 4 в точку О 2 :

' X 2A = H + 1 2 +© 4 Y 2 A =- 0,5 • B • sin © 3 _ Z 2 A = 0,5 • B • cos © 3 + 1 1

Х2В = H + 1 2 +© 4 Y 2 в = 0,5 • B • sin © 3                            (2) Z 2 В =- 0,5 • B • cos © 3 + 1 1

Рассматриваем координаты точек А и В выдернутой поросли относительно осей координат x ₁ y ₁ z ₁ (рисунок 4). Очевидно, координаты относительно оси y ₁ не изменятся. Рассмотрим координаты относительно осей x ₁ О ₁ z ₁ :

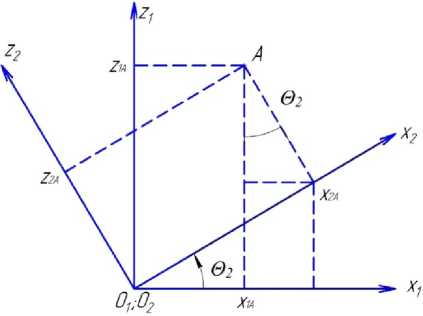
Рисунок 4. Координаты точек А и В выдернутой поросли относительно осей координат x ₁ y ₁ z ₁

Figure 4. Coordinates of points A and B of the pulled out underwood relative to the coordinate axes x ₁ y ₁ z ₁

Х 1А = Х 2А • cos © 2 - Z 2 A • sin © 2

Z ia = Х 2А • sin © 2 + Z 2 A • cos © 2

Таким образом, имеем:

X 1A = ( H + 1 2 + © 4 ) • cos © 2 — ( 0,5 • cos © 3 + 1 1 ) • sin © 2

< ^Y1 A =^{- 0,5} • sin © 3                                                            (4)

_ Z 1 A = ( H + 1 ₂ +© ₄ ) • sin © 2 + ( 0,5 • cos © 3 + 1 1 ) • cos © 2

X_iB = ( H + 1 2 +0 4 ) • cos 0 2 - ( 1 1 - 0,5 • cos © 3 ) • sin © 2

< У 1 в =^- 0,5 • sin © 3                                                            (5)

_ Z 1 _B = ( H + 1 2 + 0 4 ) • sin 0 2 + ( 1 1 - 0,5 • cos © з ) • cos 0 2

Рассматриваем поворот системы координат % i y i z i относительно оси z i на угол 0 i . Определяем координаты точек А и В выдернутой поросли в системе координат x y z (рисунок 5). Очевидно, координаты z не изменятся. Рассмотрим координаты относительно осей х и у .

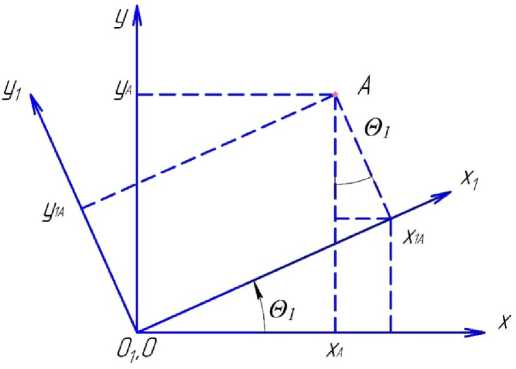
Рисунок 5. Координаты точек А и В выдернутой поросли в системе координат x y z

Figure 5. The coordinates of points A and B of the pulled out underwood in the coordinate system x y z

X а = X ia • cos 0 i - Y i a • sin 0 i

Z a = X ia • sin 0 i + Y i A • cos 0 i

Аналогичные выражения можно получить и для точки B выдернутой поросли. Окончательно имеем:

X a = [( H + 1 2 +0 4 ) • cos 0 2 - ( l i + 0,5 • cos 0 3 ) • sin 0 2 ] • cos 0 i +

+ 0,5 • B • sin 0 3 • sin 0 i

< Y a = [( H + 1 2 +0 4 ) • cos 0 2 - ( 1 i + 0,5 • cos 0 3 ) • sin 0 2 ] • sin 0 i -

• -    0,5 • B • sin 0 3 • cos 0 i

Z a = ( H + 1 2 +0 4 ) • cos 0 2 - ( 1 i + 0,5 • cos 0 3 ) • cos 0 2

X b = [( H + 1 2 + © 4 ) ' cos © 2 - ( 1 1 — 0,5 ' cos © 3 ) ' sin © 2 ] ' cos © 1 —

• -    0,5 • B • sin © з • sin © 1

* Y g = [( H + l 2 + © 4 ) • cos © 2 — ( 1 1 — 0,5 • cos © з ) • sin © 2 ] • sin © 1 +               (8)

+ 0,5 • B • sin © 3 • cos © 1

_ Z _B = ( H + l ₂ +© 4 ) • sin © ₂ + ( l 1 — 0,5 • cos © 3 ) • cos © ₂

На основании математической модели, описывающей движение характерных точек манипулятора и поросли, рассчитаем траектории их движения для следующих условий: скорости звеньев «1 = 0,628 c-1, «2  0,105 c-1, «3 = 0, V4= 0,1 м/с (рисунки 6 и 7). Время моделирования t = 5 c. Высота поворотной колонны 2 м, длина стрелы 2 м, длина рукояти 1,1 м, высота поросли 1 м.

Таблица. Исходные значения координат точек для расчёта

Table. The initial values of the coordinate points to calculate

№ п/п	Обозначение точек	Координаты точек
		X, мм	Y, мм	Z, мм
1	О 1	0	0	0
2	О 2	0	0	1850
3	О 3	1624	0	969
4	О 4	2085	0	719
5	А	2213	0	1006
6	В	2152	0	3

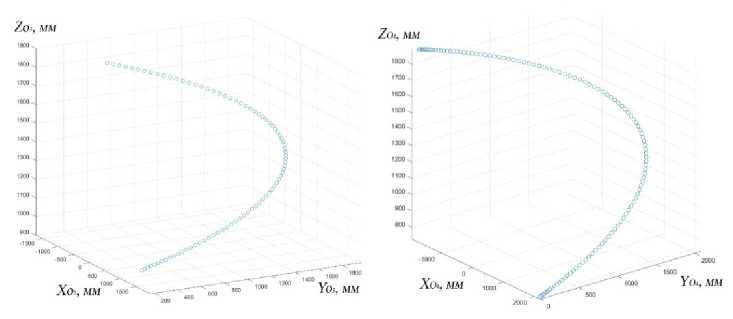
Рисунок 6. Траектории движения точек О 3 , О 4 манипулятора

Figure 6. Trajectories of movement of manipulator points O 3 , O 4

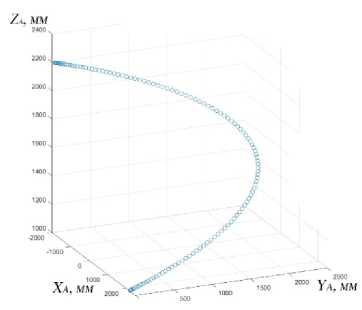
Рисунок 7. Траектории движения точек А и В поросли

XU, ММ '™ зк»

Figure 7. Trajectories of movement of underwood points A and B

4.    Обсуждение и заключение

• 1.    На основании полученной имитационной модели манипулятора были установлены траектории движения характерных точек звеньев манипулятора и крайних точек выдернутой поросли.

• 2.    Найденные управляющие воздействия могут быть использованы как входные параметры для моделирования манипулятора в других средах и для создания устройства, автоматизирующего работу оператора манипулятора.