Имитационное моделирование движения быстроходной гусеничной машины с механиком- водителем

В работах [1, 2] рассмотрены вопросы управляемости быстроходных гусеничных машин (БГМ) с позиции совершенствования системы управления поворотом, в которую включены гид-рообъемный механизм поворота (ГОМП), устройство подачи топлива в двигатель и механизм раздельного торможения по бортам. Человек, управляющий движением БГМ, в этих работах специально не рассматривался. Аргументом такого подхода являлась необходимость проработки алгоритма работы автоматической системы (АС), управляющей наклонной шайбой ГОМП, при задании наиболее опасных режимов поворота (вход-выход из поворота, движение по синусоиде, маневр «переставка»). Предполагалось, что движение по дороге в реальных условиях сопряжено с менее опасными режимами.

В дальнейшем [3] этот подход развит - проведено моделирование движения БГМ по дороге, заданной набором участков различной кривизны. Причем дорога укомплектована высокочастотным кабелем, по которому ориентируется автомат, считывающий с него информацию и управляющий штурвалом. Такой подход справедлив только при том условии, что управление БГМ осуществляет автомат, реагирующий на необходимость изменения направления движения машины в соответствии с текущей дорожной ситуацией. Такое представление управления криволинейным движением БГМ не учитывает динамических свойств механика-водителя как управляющего звена.

Для системы управления (СУ) БГМ как для особо ответственной человеко-машинной системы (ЧМС) актуальной является задача учета характеристик механика-водителя, что требует обоснования математической модели последнего.

В области моделирования механика-водителя, управляющего БГМ, имеются наработки. Это в первую очередь работы МВТУ им. Н.Э. Баумана (Красненьков В.И. [6]), Курганского государ-

Расчет и конструирование

ственного университета (Благонравов А.А., Держанский В.Б. [7]). В докторской диссертации В.Б. Держанского приведена математическая модель механика-водителя (МВ), заимствованная в своё время из трудов Дж. Хендерсона и приведенная в обзорной работе Цибулевского И.Е. [8].

На первом этапе исследований за основу были взяты рекомендованные в [7] параметры модели МВ (рис. 1): коэффициент усиления А=10, постоянная времени Д = 1 с, характеризующая реакцию на текущую относительную скорость изменения курсового угла трассы, постоянная времени Г2 = V0’2 с, характеризующая исполнительный механизм человека, коэффициент затухания колебаний §=0,4, постоянная запаздывания т = 0,2 с) и проведено имитационное моделирование движения БГМ с указанными параметрами МВ.

Го(О

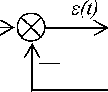
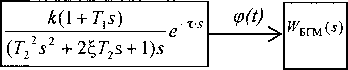
Рис. 1. Автоматизированная СУ движением БГМ

На рис. 1 Го(ц - кривизна траектории дороги, r(t) - кривизна траектории движения центра тя-

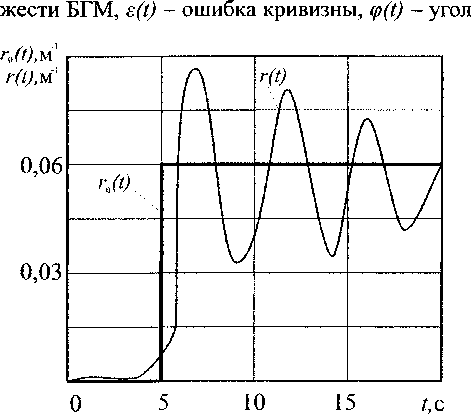
Рис. 2. Переходная характеристика автоматизированной СУ БГМ при параметрах модели МВ, взятых из работы [7]

поворота штурвала, И-бш^) - передаточная функция БГМ. Из графика переходной характеристики системы (рис. 2), полученного в Vissim и имеющего явно выраженную колебательность, следует, что качество функционирования автоматизированной СУ БГМ неудовлетворительное.

Поэтому цель данной работы - обоснование вида математической модели МВ, адекватно описывающей его реакцию на ситуацию на дороге, и выбор параметров модели, в пределах возможностей человека, исходя из желаемого качества функционирования автоматизированной СУ БГМ. Это позволит в дальнейшем, во-первых, сравнить качество функционирования автоматической и автоматизированной СУ БГМ; во-вторых, количественно оценить требования к уровню подготовки МВ.

В работах [4, 5, 8] проведен анализ влияния человеческого фактора в информационных и тех нических системах и показано, что:

• 1.    Основными свойствами человека-оператора (ЧО), в данном случае МВ, учитываемыми при его математическом моделировании, являются: свойство адаптации и время реакции, которое

• 2.    Известны квазилинейные модели (линейные при отработке фиксированного и ограниченного набора внешних воздействий) и нелинейные модели ЧО. Однако до настоящего времени ни одна нелинейная модель ЧО не доказала своей особенной полезности для инженерных целей, так как каждая из них синтезирована методом проб и экспериментов для конкретного объекта управления.

• 3.    Вид модели ЧО существенно зависит от типа слежения, последний зависит от содержания предъявляемой ЧО информации. Так, при сопровождающем слежении оператор видит и входной сигнал, и сигнал о текущем состоянии управляемого объекта. Задача оператора состоит в том, чтобы удерживать разность между этими сигналами вблизи нулевого значения. В свою очередь, модели сопровождающего слежения делятся на модели с предвидением (ЧО видит не только текущее положение цели, но и закон изменения этого сигнала на некоторый отрезок времени вперед) и модели без предвидения. При компенсирующем слежении оператор видит лишь информа-

• Кондаков С.Д., Корнаева Н.Н.,                          Имитационное моделирование движенияПавловская 0.0., Черепанов С.И.     быстроходной гусеничной машины с механиком-водителем

• 4.    Наибольшее распространение получили следующие квазилинейные модели ЧО:

складывается из трех периодов: периода восприятия входного сигнала, периода принятия решения и периода совершения действия.

цию об отклонении управляемой величины от заданного значения, ему трудно предвидеть необходимые действия, поэтому точность компенсирующего слежения ниже, чем сопровождающего.

• а)    модель Дж. Хендерсона W(s) = ^^ = —---e"^TS;                     (1)

E(s) (7V+2^Ts + l)s ф/ 5) k(A А-Т

• б)    модель Д. Макруера и Е. Крендела W (х) =----=------------- e”^TS.                  (2)

E(s) (l + 7]s)(l + r25)

В моделях (1) и (2) звено чистого запаздывания отражает запаздывание реакции ЧО, определяемое временем на восприятие входного сигнала и на принятие решения; постоянные времени знаменателей передаточных функций характеризуют инерционность нейромускульного механизма ЧО; форсирующие составляющие моделей, свидетельствующие о том, что ЧО реагирует не только на входную величину, но и на ее производную, что компенсирует инерционное запаздывание, обеспечивают устойчивость и качество отработки полезного сигнала.

Преимуществом модели (1) с точки зрения качества управления является наличие в ней идеального интегрирующего звена, благодаря чему обеспечивается точное воспроизведение ступенчатого сигнала после окончания переходного процесса. Это реальное свойство МВ (после завершения поворота БГМ продолжает движение по дороге, а не рядом с ней), которое не отражается моделью (2).

Учитывая вышесказанное при математическом моделировании МВ БГМ, решающего задачу сопровождающего слежения с предвидением, следует отдать предпочтение модели (1), хотя и с оговорками. Оговорки связаны с тем, что эта модель получена для случая компенсирующего слежения и для конкретного объекта управления (ОУ), причем в них, согласно утверждениям авторов, невозможно отделить модель человека от модели ОУ. Кроме того, в работе [8, с. 253] указано, что вообще «линейная модель ЧО, полученная для случая слежения за непрерывным случайным входным сигналом, совсем непригодна для восприятия реакции человека на ступенчатый сигнал». Действительно, форсирующее звено, реализует функцию упреждения (что очень важно для МВ видящего предстоящее изменение кривизны траектории и поворачивающего штурвал еще до начала поворота дороги) только при непрерывно изменяющемся входном сигнале Х_вх, а при скачкообразном изменении Х_вх форсирующее звено вырождается в усилительное.

Таким образом, имеющиеся в литературе математические модели ЧО не могут быть напрямую применены для описания МВ, управляющего криволинейным движением БГМ. В связи с этим разработана новая модель МВ, отвечающая специфике управления БГМ. Предложенная модель отображает свойства водителя как звена, выполняющего функцию сопровождающего слежения с предвидением. Математическая модель МВ представлена на рис. 3.

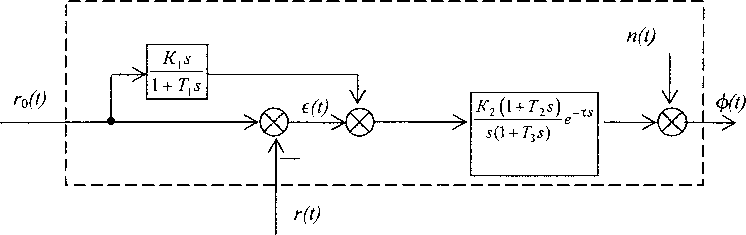
Рис. 3. Математическая модель механика-водителя

Описание математической модели МВ. На вход модели (рис. 3) поступает два сигнала: заданная кривизна дороги г_о(О и фактическая кривизна траектории движения центра тяжести БГМ г(0 в виде наблюдаемого МВ положения БГМ на дороге.

Свойства МВ как комплекса обработки информации отображают два звена: элемент сравнения, посредством которого МВ выявляет отклонение фактической кривизны траектории движения центра тяжести БГМ от заданной, и реальное дифференцирующее звено >у_МВ1 = ^ Х , кото-1 + T_vs

Расчет и конструирование

рое отражает вычисление МВ скорости изменения кривизны траектории дороги, что способствует совершению МВ упреждающих действий.

Свойства МВ как исполнителя, управляющего БГМ на основании полученной информации, КЛА^ТрЛ отражены в передаточной функции 1ГМВ2 =----------е .

На рис. 4. приведена схема моделирования системы управления БГМ с указанием числовых значений параметров модели МВ, где «кр дороги» - r₀(t), «Кг real» - r(t), «UH1» - ф(1).

Рис. 4. Схема моделирования автоматизированной СУ БГМ

Исключим человека из операции управления БГМ, заменив его автоматом, сканирующим дорогу непосредственно по высокочастотному кабелю (рис. 5).

>| кр дороги

МинТ} -

10-----

(0s+1)

Рис. 5. Математическая модель автомата, управляющего БГМ по высокочастотному кабелю

Поскольку не все дороги снабжены «электропроводом», представляет интерес сравнение качества функционирования БГМ при управлении человеком и автоматом, сканирующим дорогу. Результаты моделирования приведены на рис. 6.

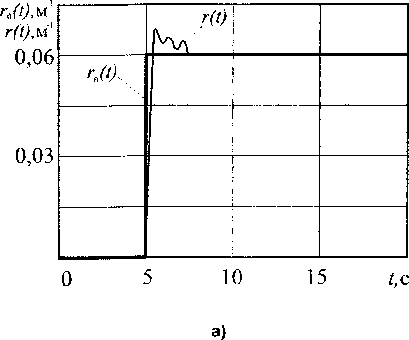
Рис. 6. Кривизна траектории движения центра тяжести БГМ при совершении тестового маневра: а - при управлении автоматом; б - при управлении человеком

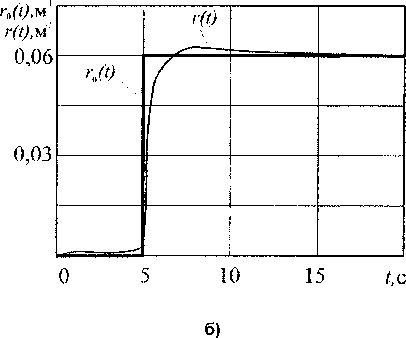
Оценим качество автоматизированной и автоматической СУ БГМ величинами прямых показателей качества, желаемые значения которых будут определяться величиной допустимого отклонения центра масс БГМ от траектории движения. Так, для БГМ в среднестатистических дорожных условиях допустимое отклонение центра тяжести БГМ от середины дороги составляет 1,5...3 м, что будет иметь место при следующих значениях прямых показателей качества системы: перерегулирование о <20 % и время переходного процесса t_x< 1с.

Кондаков С.Д., Корнаева Н.Н., Имитационное моделирование движения Павловская О.О., Черепанов С.И. быстроходной гусеничной машины с механиком-водителем

По переходным характеристикам, представленным на рис. 5, определены прямые показатели качества автоматической системы: д=20 %, ?р=2 с и прямые показатели качества управляемой человеком автоматизированной системы: а=10 %, ф=1 с. В обоих случаях выполняется условие вписываемости в коридор движения, отклонение от середины дороги не превышает 3 м.

В других вариантах расчетов, в частности, имитирующих слабую видимость, например ввиду тумана, из модели МВ исключено реальное дифференцирующее звено, отражающее предвидение дорожной ситуации. Моделирование показало, что в этом случае увеличивается время переходного процесса до 2 с.

Итак, несмотря на сложившийся стереотип о безусловном преимуществе автоматического управления, качество функционирования рассмотренной нами достаточно простой автоматической системы управления БГМ может быть ниже, чем при управлении человеком. Действительно, автомат, управляющий машиной вместо человека, наряду с положительными свойствами (отсутствием нейромускульного запаздывания реакции на ситуацию на дороге) обладает и отрицательными, в первую очередь отсутствием способности предвидеть ситуацию на дороге. Безусловно, при усложнении автоматической системы можно добиться и более высоких показателей ее качества, однако, для управления БГМ это не является необходимым.

Выводы

• 1.    Обоснована новая модель механика-водителя, управляющего криволинейным движением быстроходной гусеничной машины, которая позволяет достовернее прежних моделей описать свойства механика-водителя как звена, выполняющего функцию сопровождающего слежения с предвидением. Это позволит получить более достоверные сведения о качестве функционирования человеко-машинной системы, каковой является БГМ.

• 2.    Разработанная модель механика-водителя позволяет количественно оценить нейрому-скульные свойства механика-водителя, а также требования к уровню его профессиональной подготовки. Приведенные в работе результаты получены при Ki=0,83; Ti = 3,33 с; К₂=10; Т₂ = 1,24 с; Т₃ = 0,83 с и т = 0,12 с, что соответствует наилучшему качеству автоматизированного управления БГМ и не выходит за пределы описанных в литературе параметров моделей МВ, управляющих другими объектами.