Имитационное моделирование эпидемий компьютерных вирусов

Вирусные атаки представляют серьезную угрозу для всех пользователей компьютерных сетей, в том числе защищенных. Их успешные реализации могут привести к значительному ущербу и повлечь катастрофические последствия в различных критически важных секторах государства.

Своевременное обнаружение вредоносных программ и оперативное устранение последствий их деятельности, как показали события двухлетней давности, связанные с нападением в мае 2017 г. компьютерного вируса WannaCry на информационные ресурсы Российской Федерации, играет огромную роль в обеспечении информационной безопасности и устойчивости государственных служб и подразделений, бизнес-структур различного уровня и направленности.

Очевидно, что сетевые атаки на этом не закончились. В конце июня 2019 г. получил распространение очередной опасный вирус-шифровальщик Troldesh (Shade). Впереди – новые испытания для информационных систем, в том числе относящихся к критической инфраструктуре России. Поэтому исследование динамики распространения компьютерных сетевых вирусов является весьма актуальной задачей на современном этапе развития информационной инфраструктуры страны [1; 2].

В научных работах по данной проблематике дано описание целого ряда математических моделей распространения компьютерных вирусов в сетях [2; 3; 4; 5]. В то же время пока недостаточное внимание уделяется имитационному моделированию, дающему исследователям широкий спектр возможностей для решения задач анализа, оценки и прогнозирования процессов заражения компьютерных сетей вирусами [6]. Больше всего для имитационного моделирования указанных процессов подходят системно-динамические модели.

Системно-динамическое моделирование – направление в изучении сложных систем, исследующее их поведение во времени в зависимости от структуры элементов системы и взаимодействия между ними. Метод предложил Дж. Форрестер в конце 1950-х гг. Моделируемые процессы отображаются в виде некоторой структуры, состоящей из накопителей – уровней, соединенных взаимосвязанными потоками, которые, «перетекая», изменяют значение уровней [7].

Созданные до сегодняшнего дня модели динамики распространения компьютерных вирусов по сети, как правило, основываются на моделях эпидемических процессов [8; 9]. Самыми простыми моделями этого типа являются SI-модель (Susceptible – Infected model) и SIR-модель (Susceptible – Infected – Removed model).

В данной статье рассмотрим их усложненные модификации: SEIR-модель (Susceptible – Exposed – Infected – Removed model) и PSIDR-модель (Progressive Susceptible – Infected – Detected – Removed model).

Описание вирусных эпидемий на основе SEIR-модели

В SEIR-модели учитывается возможность того, что вирус может иметь некий «латентный период», во время которого он не наносит вреда инфицированному узлу. Обычно вирус заражает уязвимый узел ( S ) до входа в свою латентную стадию. В течение латентного периода ( Еx, Exposed ) узел считается зараженным, но не распространяет вирус. Через некоторое время он становится способным к заражению других хостов ( I ) и далее превращается в «излеченный» ( R ) (рис. 1).

Минаев В.А., Сычев М.П., Вайц Е.В., Киракосян А.Э. Имитационное моделирование...    5

Количество

уязвимых хостов (S)

I

Общее количество хостов (n)

Темп

увеличения количества

латентных

хостов

Количество

хостов в латентной стадии (Ex)

«Нормальная» скорость заражения (b)

Количество инфицированных хостов (I)

к

Количество

«вылеченных» хостов(R)

Темп увеличения количества инфицированных хостов (ExI)

Латентный период

(f)

Темп

увеличения

«вылеченных» хостов (IR)

«Нормальная» скорость иммунизации (с)

Рис. 1. Системно-динамическая SEIR-модель распространения компьютерных вирусов по сети

SEIR-модель описывается следующей системой уравнений:

dS / dt = OS (t)-SEx (t), dEx / dt = SEx (t)—ExI (t), dI / dt = ExI (t)-IR (t),

- dR / dt = IR ( t ) ,                                           (1)

SEx ( t ) =[ ^S ( t ) I ( t ) ] / n,

ExI ( t ) = Ex ( t ) / f, _ IR ( t ) = cI ( t ) .

Расшифровка обозначений, используемых в SEIR-модели, приведена в таблице 1.

Таблица 1

Условные обозначения, используемые в SEIR-модели

№ п/п	Условное обозначение элемента	Название элемента (единица измерения)
1	S	Количество уязвимых хостов (шт.)
2	Ex	Количество инфицированных узлов, находящихся в латентной стадии (шт.)
3	I	Количество инфицированных хостов (шт.)
4	R	Количество «излеченных» хостов (шт.)
5	n	Общее количество хостов в сети (шт.)
6	OS	Темп увеличения новых уязвимых хостов (шт./ч)
7	SEx	Темп увеличения латентных хостов (шт./ч)
8	ExI	Темп увеличения инфицированных хостов (шт./ч)
9	IR	Темп увеличения «излеченных» хостов (шт./ч)
10	b	«Нормальная» скорость заражения (доля/ч)
11	f	Латентный период (ч)
12	c	«Нормальная» скорость «иммунизации» (доля/ч)

6 в ыпуск 3/2019

Понятие «нормальной» скорости, введенное Дж. Форрестером [7], представляет отношение числа зараженных или излеченных хостов в день к общему количеству уязвимых хостов.

Реализована модель распространения компьютерных вирусов по сети на базе SEIR-модели в программной среде Anylogic. Общий вид интерфейса модели представлен на рисунке 2.

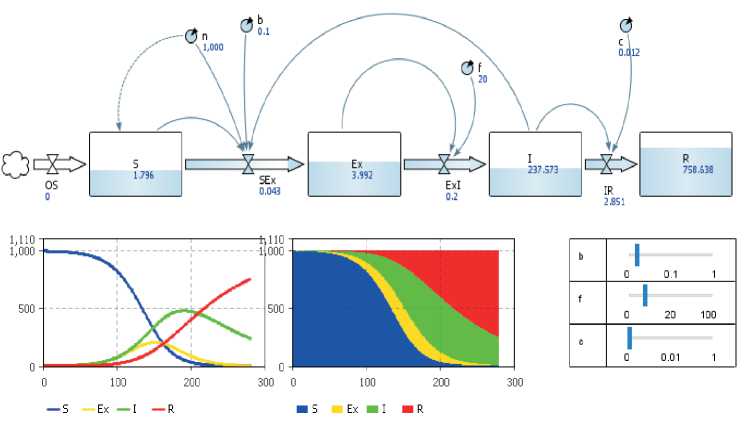
Рис. 2. Общий вид интерфейса SEIR-модели распространения компьютерных сетевых вирусов

С моделью проведен имитационный эксперимент, в котором определялось минимальное значение скорости иммунизации при заданном ограничении на максимальное количество инфицированных хостов сети.

Математическая постановка такой задачи выглядит следующим образом:

c ^ min,

I ^ I max

.

Диапазон возможных значений скорости иммунизации примем следующим: c G { 0,001; 0,03 } , шаг имитации при проведении эксперимента - 0,001.

Начальные значения других параметров модели определены следующим образом: S (0) = n = 1 000; I (0) = 2; R (0) = Ex (0) = 0; b = 0,1; f = 20 .

Оптимизационный эксперимент проведен с использованием встроенного в программу Anylogic специального алгоритма OptQuest, в котором используются как точные методы математической оптимизации, так и нейронные сети и эвристические подходы к поиску решений.

Приведем зависимости значений оптимизируемого параметра ( c ) от номера итерации при I _max = 47 и I _max= 57 (рис. 3).

Минаев В.А., Сычев М.П., Вайц Е.В., Киракосян А.Э. Имитационное моделирование... 7

На графиках нижней ступенчатой функцией отображено лучшее недопустимое значение, т.е. значение, полученное без учета ограничений, наложенных на оптимизируемую модель, а верхней ступенчатой функцией – лучшее допустимое. Можно легко заметить, что с увеличением количества итераций значение оптимизируемого параметра стремится к наилучшему значению целевой функции.

Результаты эксперимента: при ограничении количества инфицированных хостов I _max = = 47 минимальная скорость иммунизации должна составлять 0,02, а при ограничении количества инфицированных хостов I _max = 57 должна составлять 0,017.

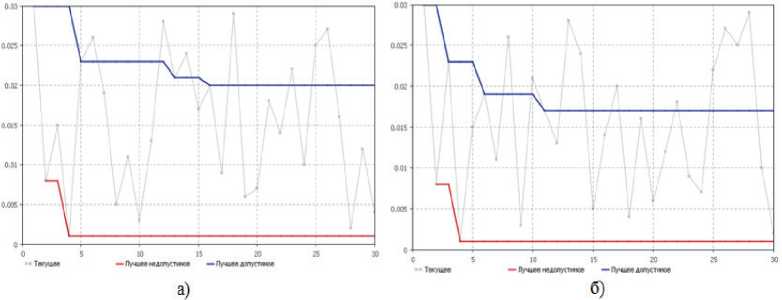
Рис. 3. Зависимости значений оптимизируемого параметра с от номера итерации: а – при I _max = 47; б – при I _max = 57

Описание вирусных эпидемий на основе PSIDR -модели

В PSIDR-модели предполагается, что эпидемические события разделены на два периода:

• •    Начальный период. Изначально вирус инфицирует один хост в сети. После этого в течение определенного времени вирус распространяется по сети, будучи не замеченным ее пользователями. Этот период характеризуется скоростью заражения b без попыток излечения. В модели начальный период обозначим как τ.

• •    Период реакции на вирус. Через период времени τ вирус обнаруживается. Осуществляется выделение его сигнатур и внесение их в базы антивирусного программного обеспечения. Неинфицированные узлы становятся невосприимчивыми к данному вирусу, а инфицированные хосты «излечиваются» по мере обновления антивирусных баз.

Таким образом, PSIDR-модель предполагает, что течение эпидемии можно разбить на два периода: вначале система может находиться в двух состояниях S → R , а по истечении времени τ система переходит в состояния S → I → D → R с возможностью и прямого перехода между состояниями S → R .

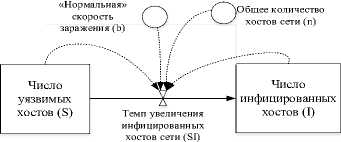
Построим схему распространения компьютерного вируса по сети на основе PSIDR-модели (рис. 4). Приведем расшифровку обозначений, используемых в PSIDR-модели (табл. 2).

Выпуск 3/2019

«Нормальная» скорость заражения (b)

Количество

уязвимых хостов (S)

Общее количество хостов сети (n)

Количество

Темп увеличения количества инфицированных хостов (SI)

инфицированных хостов (I)      <,.

Темп

увеличения

Количество обнаруженных хостов (D)

«Нормальная» скорость иммунизации (с)

Количество

Темп увеличения количества «вылеченных» хостов после заражения (DR)

«вылеченных» хостов (R)

«Нормальная» скорость обновления антивирусных баз (m)

количества обнаруженных хостов (ID)

Темп увеличения количества «вылеченных» хостов (SR)

Рис. 4. Системно-динамическая PSIDR-модель распространения компьютерных вирусов по сети

Таблица 2

Условные обозначения, используемые в PSIDR-модели

№ п/п	Условное обозначение элемента	Название элемента (единица измерения)
1	n	Общее количество хостов сети (шт.)
2	S	Количество уязвимых хостов (шт.)
3	I	Количество инфицированных хостов (шт.)
4	D	Количество обнаруженных хостов (шт.)
5	R	Количество «вылеченных» хостов (шт.)
6	SI	Темп увеличения количества инфицированных хостов (шт./ч)
7	ID	Темп увеличения количества обнаруженных хостов (шт./ч)
8	DR	Темп увеличения количества «вылеченных» хостов после заражения (шт./ч)
9	SR	Темп увеличения количества «вылеченных» хостов (шт./ч)
10	b	«Нормальная» скорость заражения (доля/ч)
11	c	«Нормальная» скорость иммунизации (доля/ч)
12	m	«Нормальная» скорость обновления антивирусных баз (доля/ч)

В начальный период модель описывается следующей системой уравнений:

dS / dt = - SI ( t ) , - dI / dt = SI ( t ) ,

SI (t )=[^S (t) I (t)] / n.

Минаев В.А., Сычев М.П., Вайц Е.В., Киракосян А.Э. Имитационное моделирование...

В период реакции модель начинает описываться следующей системой уравнений:

" dS / dt = - SI ( t ) - SR ( t ) , di / dt = SI ( t ) - ID ( t ) , dD / dt = ID ( t ) - DR ( t ) , dR / dt = DR ( t ) + SR ( t ) , ' SI ( t ) =[ ^S ( t ) I ( t ) ] / n, ID ( t ) = mI ( t ) , DR ( t ) = cD ( t ) ,

(4)

SR (t ) = mS (t).

Схема распространения вируса по сети на основе PSIDR-модели реализована в программе Anylogic. Общий вид интерфейса модели в начальный период представлен на рисунке 5, в период реакции на вирус – на рисунке 6.

Проведено два имитационных эксперимента, в которых исследуется влияние скорости заражения, скорости обновления антивирусных баз и скорости иммунизации сети на количество уязвимых, инфицированных, обнаруженных и «вылеченных» хостов сети.

Задачей данного эксперимента является исследование поведения модели в указанных двух периодах: начальный период и период реакции (табл. 3).

Таблица 3

Значения параметров и исследуемые переменные модели в экспериментах

Номер эксперимента	Значение параметров модели		Значение переменных модели
	m	c	S	I	D	R
1	0	0	S 1 ( t )	I 1 ( t )	D 1 ( t )	R 1 ( t )
2	0,04	03	S 2 ( t )	I 2 ( t )	D 2 ( t )	R 2 ( t )

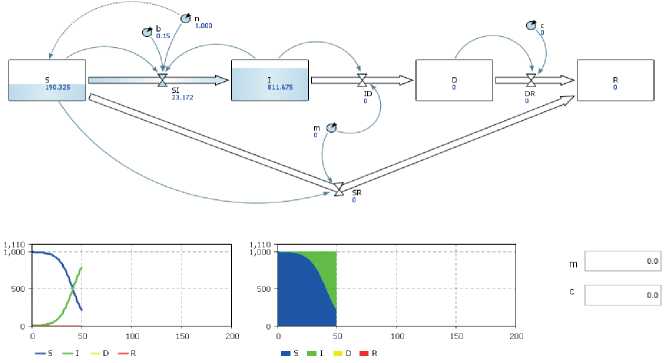
Рис. 5. Общий вид интерфейса PSIDR-модели распространения вируса по сети в начальный период

10 в ыпуск 3/2019

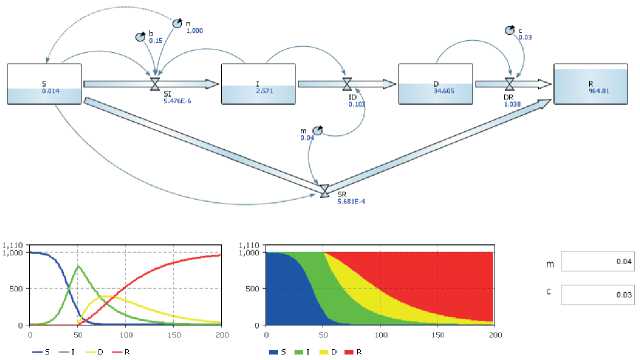
Рис. 6. Общий вид интерфейса PSIDR-модели распространения вируса по сети в период реакции

Начальные значения переменных и параметра b модели определим следующим образом: S (0) = n = 1000; I (0) = 2; R (0) = 0; D (0) = 0; b = 0,15.

Приведенные на рисунке 7 кривые отражают динамику уязвимых, инфицированных, обнаруженных и «излеченных» хостов сети во время двух периодов работы модели.

Первый - начальный (предварительный) - период (при t <т ) отражает только динамику уязвимых и инфицированных хостов сети, так как параметры m – «нормальная» скорость обновления антивирусных баз и c – «нормальная» скорость «иммунизации» в это время равны нулю.

Второй период – реакции (отклика) (при t ≥τ ) отражает уже динамику всех рассматриваемых состояний системы. В экспериментах длительность начального периода т = 50 ч.

Предварительный период Период отклика                ^{Предварительный период Период отклика}

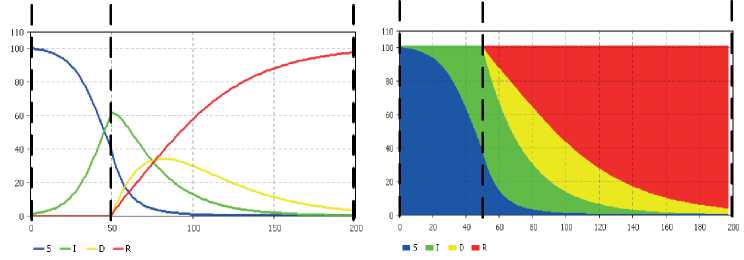
а)                                                              б)

Рис. 7. Динамика состояний PSIDR-модели распространения вируса по сети в двух периодах ( б – диаграмма с накоплением)

Минаев В.А., Сычев М.П., Вайц Е.В., Киракосян А.Э. Имитационное моделирование...    11

Таким образом, эксперименты наглядно демонстрируют качественные различия работы модели на различных временных отрезках (начальном периоде и периоде реакции).

Выводы

• 1.    Применение имитационного моделирования предоставляет новые возможности для исследования вирусных эпидемий в компьютерных сетях, а именно возможность решать задачи управления эпидемиями, прогнозирования их течения, определения оптимальных параметров противодействия и др.

• 2.    Системно-динамические модели распространения компьютерных вирусов по сети, основывающиеся на эпидемических SEIR- и PSIDR-моделях, позволяют исследовать динамику «заражения» сети и выявлять степень влияния наиболее критичных факторов. Реализация построенных моделей в программной среде Anylogic дает возможность наглядно отображать эпидемии компьютерных вирусов при различных значениях параметров модели.

• 3.    Проведенные имитационные эксперименты позволяют прогнозировать динамику числа уязвимых, инфицированных, латентных, обнаруженных и «излеченных» хостов сети в зависимости от различных значений параметров моделей, а также определять оптимальные значения параметров моделей при заданных ограничениях на характеристики распространения вирусов.

• 4.    Дальнейшим развитием работы является построение комплекса моделей, учитывающих другие процессы, связанные с распространением вирусов [10; 11; 12], и проведение дополнительной серии имитационных экспериментов с различными комбинациями учтенных факторов, включая специфические факторы конкретных критических инфраструктур.