Имитационное моделирование процесса медленной пространственно неоднородной коагуляции

Актуальность темы исследования определяется тем, что явление коагуляции, т.е. объединения мелких частиц дисперсных си -стем в более крупные, является достаточно распространенным в реальных практических задачах в области метеорологии и экологии, материаловедении, и т.д.

Необходимость применения математического моделирования для описания динамики систем коагулирующих частиц объясняется необходимостью построения соответствия между распределением частиц в реальных физических системах и решениями уравнения Больцмана. В настоящее время найдены точные решения уравнения Больцмана для сравнительно простых случаев малых градиентов температуры, скорости и концентраций в газе. Уравнение коагуляции Смолуховского, описывающее динамику коагулирующих дисперсных систем зачастую не имеет классического аналитического решения, что делает необходимым применение методов прямого имитационного моделирования для описания состояния системы.

Широкий сп ектр приложений теории коагуляции в науке и технике ставит задачу разработки адекватных математических моделей динамики дисперсных систем, состоящих из взаимодействующих между собой частиц, их обоснования и тестирования, а также создания алгоритмов и программного обеспечения для имитационного моделирования на уровне отдельных частиц, основанного на применении метода Монте-Карло.

Рассмотрим систему, состоящую из статистически большого количества хаотически движущихся вдоль одной оси частиц. Ключевой характеристикой, определяющей поведение частицы, является ее масса m. Для упрощения, без ограничения общности, ограничим значения масс частиц натуральными значениями. Скорость переноса частиц системы между актами взаимодействия vm зависит от их мас- сы. В процессе своего движения частицы системы испытывают парные соударения.

Слияние двух частиц с массами m1 и m2 в кластер суммарной массы происходит с не- которой вероятностью Φm,m, которая опре- деляется особенностями рассматриваемых физических систем. Пусть концентрация частиц массы m в окрестности точки x в момент времени t > 0 равна um (x, t), m = 1,2, .„ .

Эволюция множества конц ентраций частиц различных масс во времени определяется решением задачи Коши для пространственно неоднородного уравнения Смолуховского:

∂ u_m ( x , t ) + _v ∂ u_m ( x , t ) ∂ t ^m ∂ x x ∈ R , m ∈ N ,

Sm(u(x,t)), t≥0,

где оператор столкновений Смолуховского

1 m-1                       ∞ m ,               m-j,j m-j j m      m,jj

2 j =1                          j =1

Уравнение (1) дополняется начальными данными:

uk(x,0) =uk(x) >0, keN,  xeR (3)

при I >  2 , входит в одну из пар п ⁽¹⁾( t_n ),..., п ^{( 1 - 1)}( t_n ), то для пары п ^{( 1} ) ( t_n ) коагуляция в

Теорема существования обобщенных решений задачи Коши (1) - (3) доказана в [1] методом компенсированной компактности для последовательности гладких неотрицательных решений конечномерных задач (1)—(3)

{ u mM } при M ₀ ^^ , полученных заме- I ’ ⁰ J m ₀=1

ной оператора (2) в уравнении (1) его конечномерными аппроксимациями S kM ⁰ ) = i mM ⁰ ) S m ( I ⁽ M ⁰ ) "  u ), где I _m ^{M 0)} - индика

системе в момент времени t_n не происходит.

Тем самым исключаются многократные взаимодействия для каждой частицы коагулирующей системы.

Подсчитаем вероятность выбора пары взаимодействующих частиц с номерами ( i , j ) 1 <  i <  j <  N . Вероятность выбора этой пары

тор натуральных чисел, не превосходящих M ₀ .

Во множестве пространственных координат размещены частицы, занумерованные натуральными числами 1 <  i <  N , N >  1 . Каждому номеру i соответствует величина m i ( t ), которая равна массе i -й частицы, а ее пространственные координаты обозначим x i ( t ) . Если m i ( t ) = 0 для всех ячеек, то частица с номером i отсутствует в системе. Условимся, если частица присутствует в системе, то она может находиться в данный момент времени только в одной ячейке. Таким образом, в каждый момент времени состояние системы задается распределением масс m ( t ) = { m i ( t ) } N 1 и пространственных координат ^{{ x} i ⁽ t ^)} N

Пусть значения времени t принимают дискретные значения t n = пт , n e Z ⁺ , т > 0 .

на   s-м шаге в серии независимых испытаний равна:

(с 2 Y^{- 1} 1

N -2       ¹

р 2       " х~<2 ,

V CN 7  CN

1 <  I <  Q ( N )

где первый сомножитель является вероятностью того, что в первых ( s - 1) -м испытании во множестве А не появлялась пара с заданными номерами частиц i или j . Второй сомножитель - это вероятность выбора искомой пары на последнем шаге. Таким образом, вероятность выбора пары ( i , j ) из множества А на одном из шагов в серии 1 <  s <  Q ( N ) независимых испытаний равна сумме геометрической прогрессии указанных вероятностей, которая равна:

1 -

, 2   А б ^{( N} )

N - 2

<х 2

’2 _С2

N   C N - 2

Если число повторных испытаний Q ( N ) по

Частицы системы в момент времени t_n могут участвовать в парных взаимодействиях, приводящих к их коагуляции. Акты парных столкновений и коагуляции разыгрываются случайным образом так, что:

выбору пары взаимодействующих таково, что величина Q ( N ) N ^{- 1} ^^ , больших значениях N имеем:

частиц

то

при

1 -

• N - 2 г-, 2

у Q ( N )

P ■' ⁾( t n ) = ( i , j ) } = 1/ C N .        (4)

С ² -С²

N '-'N - 2

~--

2 N

Возможность

1 <  s <  Q ( N )

коагуляции

выбранных вышеуказанным способом

для пар

Возможные пары сталкивающихся частиц системы в момент времени t_n выберем Q ( ^N )

как значения набора { п ⁽) ( t _n ) } , накладывая дополнительное ограничение: если хотя бы один из номеров, входящих в пару п ^{( 1} ) ( t_n )

номеров сталкивающихся частиц определим розыгрышем совокупности независимых

случайных величин n ( ij ) ( t _n ), ( i , j ) eA ) , принимающих два значения: 0 и 1. Значение 0 означает запрет коагуляции, а 1 - наличие коагуляции для пары частиц с номерами ( i , j ) если их пространственные координаты в мо-

мент времени tn подчиняются условию | xt (tn) - xj (tn) |< h , где h > 0 - характерный пространственный масштаб парного взаимодействия частиц. Розыгрыш этих значений подчиним следующим правилам. Положим, что п(j,,)(tn) = 0, если mi(tn)mj(tn) = 0, т.е. при отсутствии, по крайней мере, одной из частиц в паре коагуляция не происходит. Если mi (tn)mj (tn) > 0, то значения случайной ве личины п (i ,)(tn) задаются условной функцией распределения:

P ^{{ п ( ;} , ^{j ) (} t n ) = ^{1 }} = ^ф m i ⁽ t n ), m j ⁽ t n ),          (8)

P ^{{ п ( ;} , ^{j ) (} tn ) = ⁰ } = 1 ^-ф m i ⁽ t n ), m j ⁽ t n у     (9)

^{где 0} < ^ф m 1 , m ₂ = ^ф m ₂, m 1 <  ^1— вероятность коагуляции сталкивающейся пары частиц с массами m 1 и m ₂ .

Если пара ( i , j ) еА выбрана и значение П ( _ii ) ( t n ) = 1, то значение вектора состояния m ( t n ) преобразуется по следующему правилу:

ma(tn) ^ma(tn) = ma(tnX a * i,   (10)

mi (tn ) ^ mi (tn ) = mi (tn ) + mj (tn )

mj (tn ) ^ mj (tn ) = 0-

Если же П ( _i , j ) ( t _n ) = 0 , то значения m _a (t_n ) , 1 <  a <  N остаются неизменными. Указанная процедура выполняется для всех пар выбранных номеров последовательным перебором ПХ ) ,..., П ' QN) > ( t , ) .

Рассмотрим числа заполнения пространственных ячеек с ц ентром в заданных точках x ^{( 1} ) е Ox , которые обозначим:

def

D₁ = { x е Ox :| x - x ^{( 1} ) | < —},

2(11)

частицами массы m е N :

def N

№( t n ) = Ж . m ( 1 . 1 (0.5 h - | x ( t , ) - x ( ¹ > |).

i =(12)

Здесь 0- функция Хевисайда. Вышеуказанной процедуре розыгрыша актов коагуляции сталкивающихся частиц в ячейке Dl соответствует преобразование чисел за полнения N1)(tn) ^ N1)(tn).

После завершения розыгрыша актов слияния частиц коагулирующей пространственно неоднородной системы осуществляется перемещение частиц вдоль пространственной оси. Положим, что vm - скорость про- странственного переноса частицы массы k ∈ N . Размер пространственных ячеек h и шаг по времени т подчиним условию Th-1 = 1 . Тогда, если частица с номером i имеет массу m, то за время т она перемещается в пространстве Ox по закону xi (tn + т) = xi (tn) + vmT .

Тем самым определяется состояние коагули рующей системы в момент времени tn+1.

Далее вновь разыгрываются акты коагуляции, осуществляется пространственный перенос и т.д. Таким образом, полностью определена эволюция системы для всех t_n >  0 .

Обозначим величиной Nm)')(tn )^ среднее число частиц массы m в ячейке Dl в мо мент времени tn > 0. Положим:

и ( ¹ ) u m , N

( t n ) =

def kN ⁽ l ¹

Nh

• - средняя концентрация частиц массы m в ячейке D₁ в момент времени t_n .

Воспользуемся приведенной в работе [2] разностной схемой для поиска решения задачи Коши уравнения Смолуховского.

Для проверки корректности построенной модели воспользуемся условиями тестовых примеров работ [3], [4].

Положим начальные условия и значения ядер коагуляции:

• ^ф m_b m ₂ = m 1 ^{- m} 2| ,

^ 1 ( x ) = Ф 2 ( x ) = 72 0 ( x ) 0 (1 - x ), | x| <^.

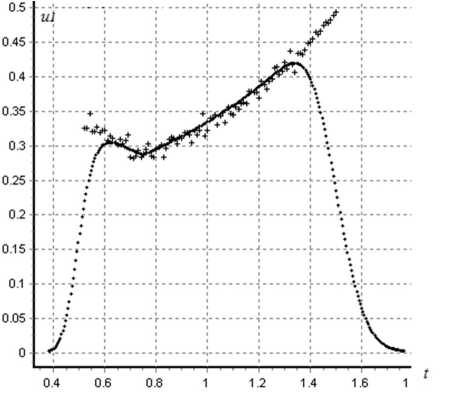
Рисунок 1 - Начальная загрузка 10 тыс. частиц;

–– Разностная схема, +++ Вычислительный эксперимент. Сечение u ₁ ( t ) пpи x = 1,5.

В сл едующем тестовом примере поло- жим интенсивность коагуляции, начальные скорости и массы частиц в виде:

Ф =1.

m ₁, m ₂       ,

vk

(-1) k k,

^{ф (} x ) =

e x ,0 <  x <  1

2 k     ,

0, x >  1

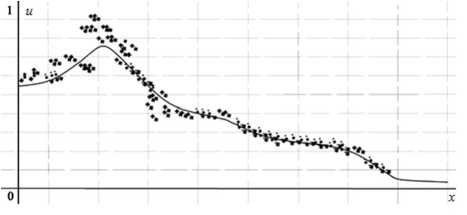
Рисунок 2 - Начальная загрузка 20 тыс. частиц –– Разностная схема, +++ Вычислительный эксперимент. Полная концентрация u ( x ) пpи t = 0,5.

На основе анализа полученных данных можно сделать вывод о наличии достаточно хорошего согласования между р езуль-татами предложенного алгоритма прямого имитационного моделирования и аналитическими решениями задачи Коши для уравнения Смолуховского пространственно неоднородной коагуляции.