Имитационное моделирование в системах автоматизации диагностики изделий машиностроения

Применяемые методы настройки приборов для неразрушающего контроля, использующие электромагнитные датчики, связаны с изготовлением и экспериментальным исследованием настроечных образцов с известными (а зачастую и заданными) свойствами. Причем количество этих образцов должно быть статистически значимым (иногда более 100 штук). Изготовление такого количества образцов и исследование их физико-механических свойств требует как больших финансовых затрат, так и затрат времени, что делает невозможной быструю переналадку системы контроля на новую задачу.

Проблему можно решить, если применить компьютерное моделирование [1]: математическая модель описывает связь между сигналом датчика и физико-механическими свойствами изделия, а имитационная модель позволяет создавать «виртуальные» образцы изделия с требуемыми свойствами. Таким образом, методом компьютерного эксперимента возможно определять оптимальные условия контроля и находить значения коэффициентов для настройки приборов неразрушающего контроля.

Физико-математическая модель образования сигнала датчика. В приборах неразрушающего контроля в качестве накладного электромагнитного преобразователя часто используется датчик, показанный на рис. 1.

Изделие с переменными по толщине (координате Х) свойствами представляется состоящим из n тонких слоев, имеющих неизменные электромагнитные свойства: толщину h, комплексную магнитную проницаемость ц, электропроводность с, коэффициент Рэлея х. Датчик состоит из ферромагнитного сердечника с намотанными на нем возбуждающей обмоткой W1 и измерительной обмоткой W2. Он расположен над контролируемым изделием с зазором δ [2].

Электромагнитное поле в проводящей среде описывается уравнениями Максвелла:

—              —                                              —                         —

rot H = σ E ,           rot E = - j ωµ H .

Для схемы расположения датчика над контролируемой средой можно записать граничные условия:

∂ H _{= 0,} ∂ Z

∂ E _{= 0,} ∂ Z

H_Z = 0 .

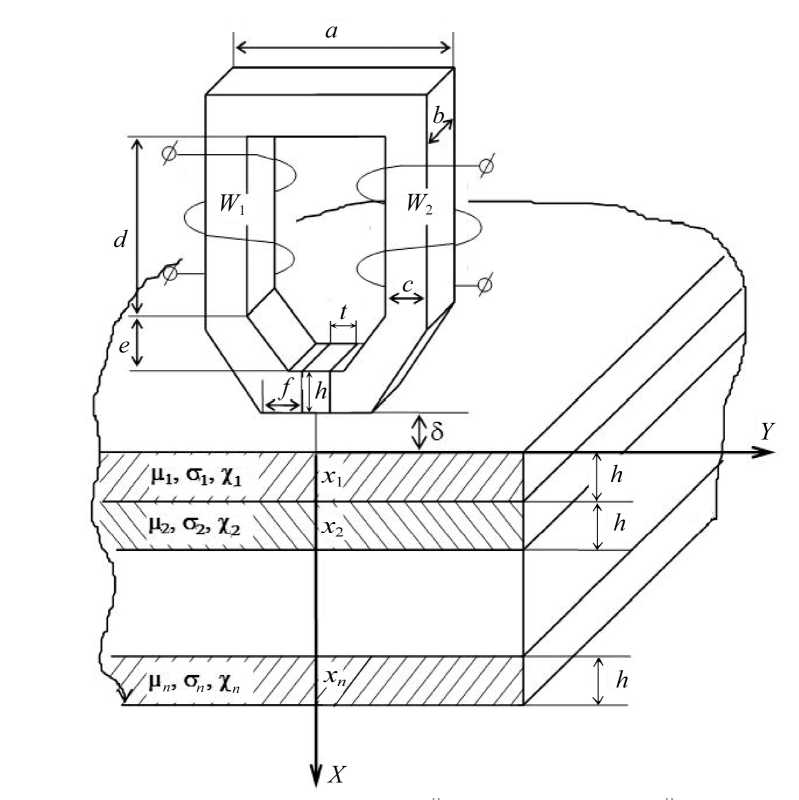
Рис.1. Электромагнитный датчик, расположенный над многослойной контролируемой средой

Следовательно,

E x = 0,   E y = 0 ,

дH _x   ⁶ H y

—

д y    д x

= G E z

—- = j ®H H ¹ X . д y

Получаем уравнение:

д ² E_z   д ² E_z

— j ЮЦС E z = 0 ,

zz дy2

которое является однородным уравнением Гельмгольца в декартовой системе координат:

д2 Ez   д2 Ez

---z- +---z- + m Ez = 0 , дx2    дy2

где m = — j шца .

Дальнейшее решение уравнения позволяет определить ЭДС датчика [3]:

•

•

(       ()иС7^

E = — W_vWJj to — +  -- =m-

' ²⁷ ( = m ,   2 B + A= m”

4 A 1 A + CZ') . kn) + J. '--mrsi Sm n2 . k2 B + AZ(mk)    2 J

Полученное уравнение можно использовать для определения сигнала электромагнитного датчика в имитационной модели. Для примера приведено сравнение моделированных и измеренных на образцах изделий сигналов датчика, из которого хорошо видно практически полное их совпадение (рис.2).

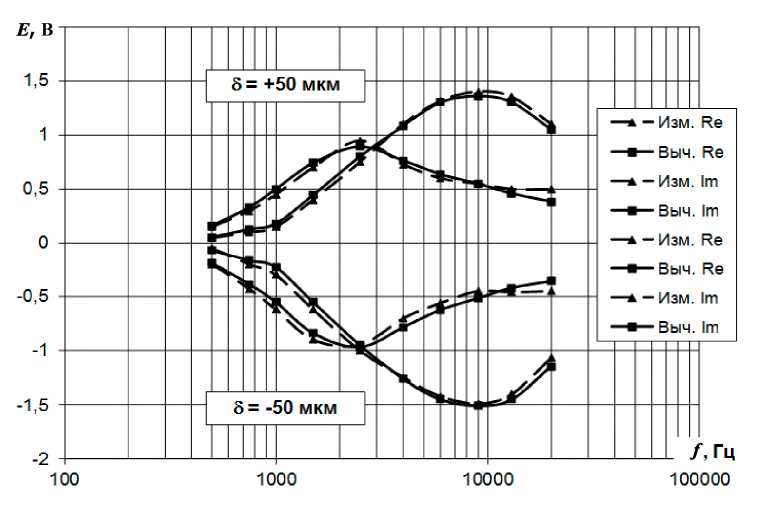
Рис.2. Сравнение амплитудно-частотных характеристик моделированного и измеренного на образцах изделий сигналов при различных относительных зазорах между датчиком и изделием

В ряде случаев, применение основных колебаний для электромагнитного контроля приводит к недопустимой погрешности. Например, ЭДС датчика в зависимости от толщины упрочненного слоя определяется, главным образом, отражением электромагнитной волны от поверхности, разделяющей упрочненный слой и основу. Упрощенно зависимость ЭДС от толщины упрочненного слоя в этом случае определяется коэффици ентом отражения:

^{µ 1 σ 2} - 1 , (*) µ ₂ σ ₁

где µ 1 и σ 1 соответствуют упрочненному слою, а µ 2 и σ 2 – основе.

При всех известных видах упрочнения, вызывающих физические дефекты в идеальном кристалле железа, магнитная проницаемость ц _t и удельная электропроводность с _; упрочненного слоя уменьшаются по сравнению с магнитной проницаемостью ц 2 и удельной электропроводностью σ ₂ основной стали. Если µ и σ изменяются пропорционально, то выражение (*) стремится к нулю, и преобразователь теряет чувствительность к толщине упрочненного слоя. В действительности выражение (*) не равно нулю, но близко к нему. Сигнал отраженной волны на границе раздела слоев настолько мал, что его превосходят помехи, вызванные вариациями электромагнитных свойств изделия. Это и является причиной возникновения недопустимо большой ошибки при контроле некоторых видов упрочнения по основным гармоникам сигнала преобразователя.

Исследование зависимости информативности комбинационных колебаний по сравнению с основными показало, что в ряде случаев комбинационные колебания значительно информативнее. Несмотря на то, что на комбинационные колебания сильно влияет зазор между датчиком и контролируемым изделием, влияние толщины упрочненного слоя на них гораздо сильнее. Поэтому отношение полезного сигнала к помехе в них больше, чем в основных гармониках. Использование комбинационных колебаний повышает точность контроля толщины упрочненного слоя.

Например, при упрочнении борированием коэффициент отражения [см. формулу (*)] равен 0,058, тогда как аналогичный коэффициент для комбинационных колебаний равен 0,44 – это почти в десять раз выше.

ЭДС комбинационных колебаний в слабых полях рассчитывают, учитывая коэффициент

Рэлея х и то, что электромагнитные свойства слоев изделия изменяются по глубине (см. рис.1).

Решение двумерного дифференциального уравнения Гельмгольца для каждого i -го слоя модели имеет вид:

Hyi ^ — ^A k [ Aik exp( - j^ikx ) ^{- C}ik ^e xp( j^ikx ) ] c ^os ^ikУ . ^юЦ к

Граничные условия между слоями i и i + 1 можно представить выражениями:

Х ⁽ x )

— [ A iк ^exp ( j ^ ⁽ x ) x i ) ^- C ik exp ⁽ j ^ ⁽ к) x i ) ^]=

Ц i

x ( x )

i ^{+ 1}, ^k j                     ⁽ x )                                ⁽ x )

= .     LAi+1,k exp( J^i+1,kxi) Ci+1,k eXp( J^i+1,kxi) ] , ц i+1 -

^Aik ^ex p ^{( -} J ^ x ) xi ) ⁺ C ^ ik ^ex p ⁽ J ^ x ) xi ) =

= A i + 1, k exp ^{( -} J ^M, k x i ) + C ^ i + 1, k exp ⁽ J ^m , k x i ).

В последней (n+1)-й области металла (т.е. на бесконечно большой глубине) электромаг нитное поле полностью затухает, поэтому при x ^да Hn+1,y > 0 и Hn+1,x ^ 0. Такое возможно при An+1,k = 0 .

В модели выбирается большое количество настолько тонких слоев, что напряженность магнитного поля внутри каждого слоя изменяется менее чем на 1%. Большим количеством слоев достаточно точно дискретно отражается непрерывное распределение электромагнитных свойств упрочненного слоя и основного металла.

Напряженность поля в указанных точках определяется как функция времени:

H yi = H mi sln ⁽ ® t + V i ) .

Приведенная последовательность повторяется дважды для двух частот ю 1 и ю ₂ основных колебаний тока возбуждения преобразователя, которые в нелинейной среде, взаимодействуя, образуют комбинационные колебания.

Чтобы комбинационные колебания отличались по частоте от основных колебаний и их высших гармоник, основные частоты должны относиться как достаточно большие целые взаимно простые числа N и M :

ю , : ю ₂ = N : M .

Напряженность результирующего поля в точке x_i :

H i = ^Hm ,1, i ^Sin( ® 1 t ⁺ V 1 i ) ⁺ H m ,2, i ^Sin( ® 2 t ⁺ V 2 i ^).

Получившееся колебание – периодическое; его период составляет

T = ^^ N = ^^ M .

^ю 1      ^ю 2

Непрерывно изменяющаяся во времени напряженность вычисляется дискретно через интервалы времени At. Если ограничить спектр сигнала суммарными комбинационными колеба- ниями третьего порядка, то, по теореме Котельникова, интервал времени

A t =

T

2 N + 4 M

Индукция магнитного поля в точке x_i в момент времени t_p определяется уравнением Рэлея:

B ip = Й i H ip + X iH^p sign H ip .

Рабочий поток магнитной индукции в контролируемом изделии рассчитывается заменой интеграла суммой: ^∞              n + 1

Φ _p = b ∫ B_pdx ≈ b ∑ B_iph_i ,

₀                 i = 1

где Φ _p есть дискретная функция времени.

Гармоническим анализом переменного магнитного потока можно определить вещественную и мнимую составляющие потока суммарных комбинационных колебаний третьего порядка:

Φ _ком = ² Φ ( t )sin(2 ω ₂ +ω ₁) tdt ≈ ² ∑ Φ _p sin ^{2 π} (2 M + N ) p ,

T 0                         m p = 1         m

Φ _к ^j _ом = ² Φ ( t ) cos(2 ω ₂ +ω ₁) tdt ≈ ² ∑ Φ _p cos ^{2 π} (2 M + N ) p ,

T 0                        m p =1        m где m – число интервалов времени Δt, на которые разбит период.

Комплексная амплитуда рабочего потока:

Ф „ ком

= Ф „ ком

+ j Φ

ком

частично сцеплена со вторичной обмоткой преобразователя, поэтому комплексная амплитуда комбинационных суммарных колебаний третьего порядка рассчитывается следующим образом [4]:

Э _ком = - j ( ω ₁ + 2 ω ₂)W₂ Φ′ _ком .

Подобным образом с помощью гармонического анализа магнитного потока в математической модели вычисляются ЭДС основных колебаний и разностных комбинационных колебаний третьего порядка. Принципиально возможно и вычисление высших гармоник.

Имитационная модель создания виртуальных образцов. Предназначена для имитации виртуального прибора для неразрушающего контроля, виртуальных образцов, ЭДС сигналов измерительного преобразователя (датчика), вычисления линейной регрессионной модели по сигналам основных и комбинационных колебаний, а также определения ошибки контроля на виртуальных проверочных образцах.

Имитационная модель реализована в виде программы для ЭВМ. Структурная схема имитационной модели показана на рис.3. При моделировании вычисляются ЭДС датчика для набора значений либо зазора, либо толщины упрочненного слоя. Кроме того, при вычислении ЭДС происходит случайное варьирование электромагнитных параметров виртуального образца изделия, а также случайное варьирование того параметра, который не варьируется детерминирован-но. В конце моделирования к полученным значениям ЭДС добавляются случайные значения, имитирующие аддитивную и мультипликативную погрешности прибора для неразрушающего контроля. Такие вычисления ЭДС датчика производятся для заданного ряда частот как основных, так и комбинационных колебаний.

На рис.4 показана структурная схема блока вычисления ЭДС сигналов измерительного преобразователя при детерминированном варьировании зазора между датчиком и изделием. Аналогичный вычислительный блок используется при детерминированном варьировании толщины упрочненного слоя, тогда производится цикл не по значениям зазоров, а по значениям толщин упрочненного слоя.

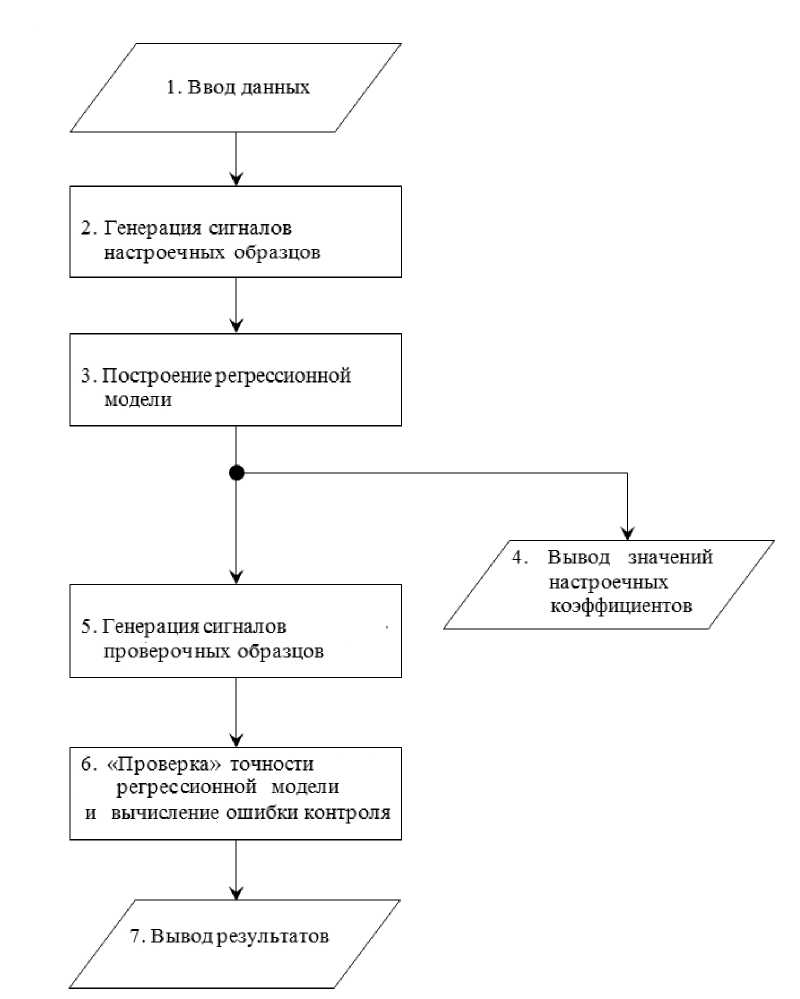
Рис.3. Структурная схема имитационной модели

В системе создается два набора виртуальных образцов – настроечные и проверочные. Настроечные образцы используются для построения регрессионной модели. После получения коэффициентов уравнения регрессии, в это уравнение подставляют значения сигналов, полученные на проверочных образцах. То есть в этом случае имитируется процесс измерения контролируемого параметра виртуальным прибором для неразрушающего контроля. Результат этой операции – показания прибора, получающиеся при измерении образца, не участвовавшего в настройке. Оба набора виртуальных образцов могут различаться между собой.

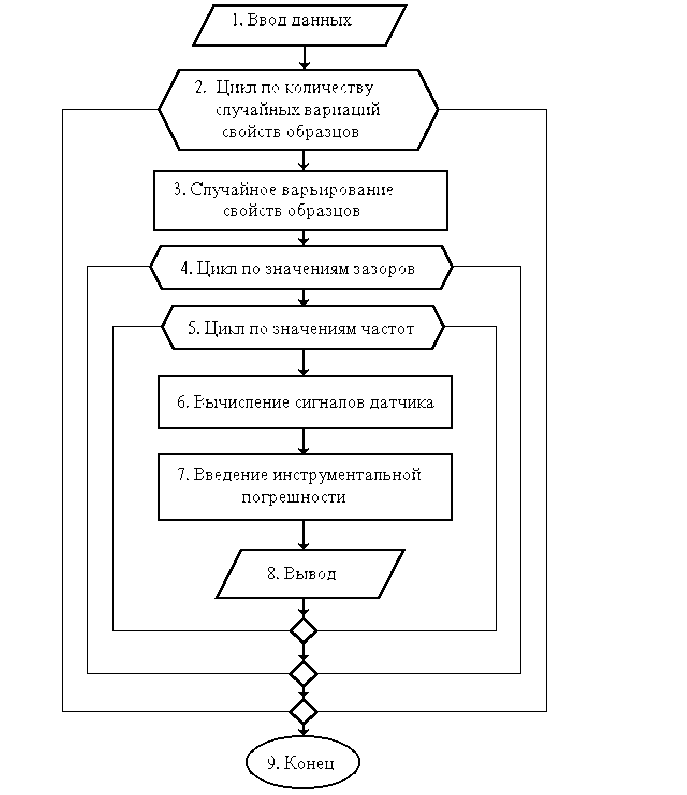
Рис. 4. Структурная схема вычислительного блока ЭДС сигналов измерительного преобразователя

При моделировании возможно задавать различные начальные условия для массивов настроечных и проверочных образцов. Например, количество настроечных образцов можно задавать небольшим, чтобы оценить представительность выборки настроечных образцов в данных условиях контроля. Различной может быть и величина случайных вариаций электромагнитных свойств в каждом из наборов. Тогда появляется возможность определить, как повлияет ошибка в оценке параметров настроечных образцов, или что покажет прибор при контроле изделий из другой партии, отличающихся либо значениями технологических факторов, либо их разбросом.

Ошибка контроля зависит от количества настроечных образцов при различном количестве частот, составляющих спектр измерительных сигналов. С ростом количества настроечных образцов ошибка сначала падает, а потом перестает меняться. Кроме того, ошибка контроля зависит и от числа частот, составляющих спектр сигнала датчика. При малом количестве настроечных образцов с ростом числа частот, составляющих спектр, включенный в регрессионную модель, растет и ошибка контроля. Это происходит из-за снижения количества степеней свободы при построении модели и, следовательно, снижения представительности выборки сигналов.

Имитируемый образец разбивается на n слоев с неизменными электромагнитными свойствами внутри слоя. Магнитный поток в изделии вычисляется интегрированием по толщине изделия. Поэтому толщина одного слоя разбиения должна быть достаточно мала, чтобы изменение величины напряженности поля при переходе от слоя к слою также было малым. Однако при слишком большом числе слоев резко растет вычислительная ошибка и продолжительность вычислений, следовательно, требуется оптимизация числа слоев для минимизации погрешности моделирования.

Ошибка контроля зависит и от числа слоев, на которые разбивается виртуальный образец. При количестве разбиений более 1000, ошибка контроля начинает расти. Это происходит из-за накопления погрешностей округления при вычислениях с конечной точностью [5].

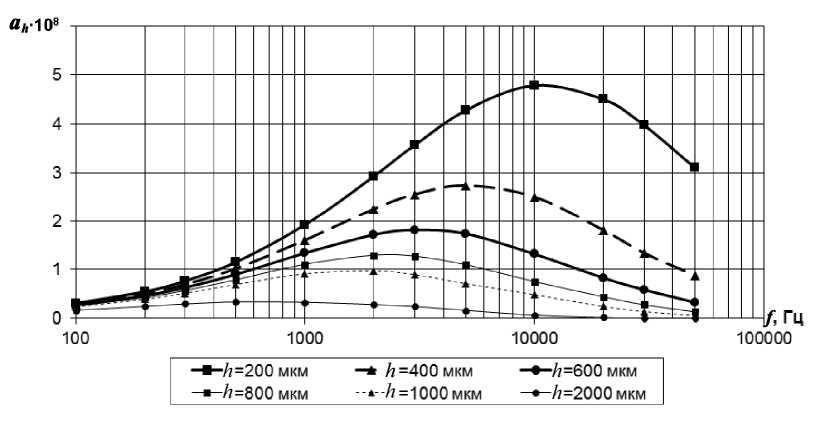
Рис.5. Частотные характеристики модуля передаточного коэффициента толщины упрочненного слоя для комбинационных колебаний

Для обеспечения высокой точности измерения контролируемого параметра должен быть установлен оптимальный спектр частот возбуждения преобразователя. Амплитудно-частотные характеристики передаточного коэффициента толщины упрочненного слоя (рис.5) позволили установить области частот возбуждения датчика, при которых он высокочувствителен к контролируемому параметру, и выбрать, таким образом, составляющие многомерного сигнала.

Заключение. Разработана математическая модель образования сигнала электромагнитного датчика, расположенного над многослойной проводящей ферромагнитной средой для основных и комбинационных колебаний. Несмотря на то, что амплитуды комбинационных колебаний намного меньше, чем основных, они оказываются более информативными. Используя комбинационные колебания, можно существенно повысить точность неразрушающего контроля. Поскольку при упрочнении значительно изменяется коэффициент Рэлея, то комбинационные колебания оказываются намного чувствительнее к толщине упрочненного слоя, чем основные.

Разработана имитационная модель образования сигнала электромагнитного датчика для основных и комбинационных колебаний. Поскольку аналитическое выражение для комбинационных колебаний не очень удобно для прямого расчета, то предложен рекуррентный метод, используя который можно достаточно просто получить значения ЭДС датчика как для основных, так и для комбинационных колебаний (а также для высших гармоник, если такое понадобится) любого порядка. Генерация виртуальных образцов и их использование для построения и проверки точности регрессионной модели позволяет определить оптимальные условия контроля без изготовления и исследования реальных образцов изделий. Кроме того, значительно сокращается количест- во реальных образцов изделий, требуемое для окончательной настройки прибора при его эксплуатации.

Усовершенствованы методы формирования и обработки сигнала датчиков в целях повышения точности контроля. Использование имитационной модели позволяет определить оптимальный спектр возбуждения датчика и параметры регрессионной модели для обработки его сигнала. Выбор оптимального спектра возбуждения значительно повышает точность контроля и уменьшает влияние на его результаты случайных вариаций свойств изделия, а также различных помех, воздействующих на устройство в целом.