Implementation of Fair-exchange and Anonymous Online E-cash Protocol for E-commerce

Published Online August 2016 in MECS

With the rapid growth of technology people are able to sell and purchase online products at a click of mouse. This new era of online purchasing is possible because of many electronic commerce transaction protocol which allows user to transact online even by not knowing to each other [6].

There are many types of e-payment methods to do online shopping like credit card, debits card etc. But the main problem with these methods is that sometimes transacting parties’ customer and merchant are not known to each other which lead to lack of security and trust. The main trust issue from customer side is that its own identity is not steal by someone on network like credit cards contains the customer information like customer pin number, card - number etc. which are unchangeable for lifetime so that, if any intruder trace information of customer he can be able to use it again or in cryptography language we can say message can be replayed. Sometimes it can be possible that fake merchant steals customer information and make fake payment. Merchant also has some trust issues like after giving product customer will pay merchant or not.

By keeping all these issue in our mind we proposed an anonymous and fair exchange protocol by using e-cash as payment method. We used e-cash as a payment method because each time a new string used by customer as an ecash for unique transaction so that intruder cannot be able to use same e-cash again and it do not contains the true identity of customer.

The main aim of our research is to propose a protocol which provides fair exchange of product/payment to both transacting parties’ and identity of customer should be anonymous to merchant or any other outsider on network.

• II.    Related Works

  In this section we are going to briefly describe some previous works and also compare our work with them. David Chaum in 1982 proposed blind signature to hide true identity of customer which is known as anonymity [6]. To achieve fair exchange in e-commerce many protocols uses off-line as well as on-line TTP protocol [13] [15].

E-cash can be implemented as offline or online. In offline, e-cash is kept by consumer in a device such as smart card or any other type of token [4].We have developed an online e-cash protocol using offline TTP model in which e-cash is kept by bank in his database.

The author [5], implements the software to keep database of electronic cash between the user and the bank. By storing e-cash on hard disk have many dis-advantages like, crashing of hard disk, stealing of hard disk and any technical fault. The author [10], proposed an online ecash protocol in which bank keeps e-cash in its database.

For achieving fair exchange many researchers’ [9] [22] [3], used on-line TTP model which ensures fair exchange but leads to bottleneck problem. In [9], author proposed a protocol in which TTP cannot read any information but only verify the intended parties i.e. customer and merchant.

To reduce bottleneck protocol author [22], proposed protocol in which bank acts as TTP but their protocol do not achieve fair exchange. To improve the performance [14], proposed a new protocol in which bank gives license to customer but it also been analyzed that their protocol breaches customer anonymity.

Many off-line e-cash schemes developed by [15] [18] [19], but it needs lots of mathematical calculation so find out the double spender of e-cash.

In this paper, we proposed an on-line e-cash protocol which does not require lots of mathematical computation for finding double spending also the e-cash stored in bank’s database in secure form. To maintain the trust between customer and merchant we used compatible keys concept. We have also analyzed our protocol with other protocols. The rest of the paper is organized as follows in section 2, we described basic concept used to develop protocol. Section 3 describes steps of protocol and result and analysis describes in section 4. We have also developed dispute protocol in which customer invokes TTP while any dispute occurs from merchant. Finally section 5, describes conclusion of paper.

• III.    Basic Concepts

In this section, we are going to describe two main properties of proposed protocol.

• A.    Blind Signature

Blind signature is a form of digital signature in which message is not seen by signer while signing. Blind signatures used to provide unlink ability, which do not allows signer to link blinded message with actual message but signer can be able to verify it and keeps sender privacy. It can be implemented by using concept of RSA. In our work we applied blind signature for signing actual value of e-cash from bank. The steps of making blind signature are given as follows: -

• 1)    Choose a random factor r in z ^∗ such that gcd (r, n) =1

• 2)    Blind e-cash using above random factor = (ecash) mod n

Now, bank will sign above blinded e-cash using his own private key and sends signed blinded e-cash to customer. After receiving signed blinded e-cash, customer un-blinds received e-cash. The steps of removing blinding factor for e-cash is describes in below steps

Signed e-cash = (е - саѕһ) db mod n)

( ∗ dbmod-n.)((e- casℎ )dbmodn) , e*d mod

n=1 (RSA property)

( r )( ⁽ e-cash ⁾ ^mochi^

Un-blind e-cash = ( e

- cas ℎ ) ^dbmodn

Here, db is bank’s private key and eb is bank’s public key and n is modulus of public and private key of bank. Z ^∗ Is subgroup of ^n which contains elements which have unique multiplicative inverse.

• B.    Compatible Keys

• i)     Let m be the product which is encrypted with the

public key (e, n1) generated by TTP whereas TTP keeps (d1, n1) with itself.

• ii)    Now, merchant also have (e, n1) and make compatible keys (e, n2) and (d2, n2) with itself. In compatible keys e should be the same where (n, d) key pairs are different.

• iii)    For proof of theorem let us take a message m encrypted with (m, e, n1) and same message encrypted with (m, e, n1*n2).

• iv)    (m, e, n1)=(m, e, n1*n2)

• v)    m^emod n1= m^emod n1∗n2

• vi)    m^emod n1= m^emod n1( mod n1)

• vii)    m^emod n1= m^emod n1

• viii)    m =  , LHS = RHS hence proved.

• IV.    Proposed Protocol

The protocol consists of five main phases; Initial setup, registration phase, Issue of e-cash phase, payment and deposit phase. We have also developed extended e-cash dispute algorithm. The block diagram of proposed protocol is given in fig. 1. Bank has three databases: client info, new coin and spend coin in which fresh coin database contains not used coin information whereas spend coin database contains used coin information.

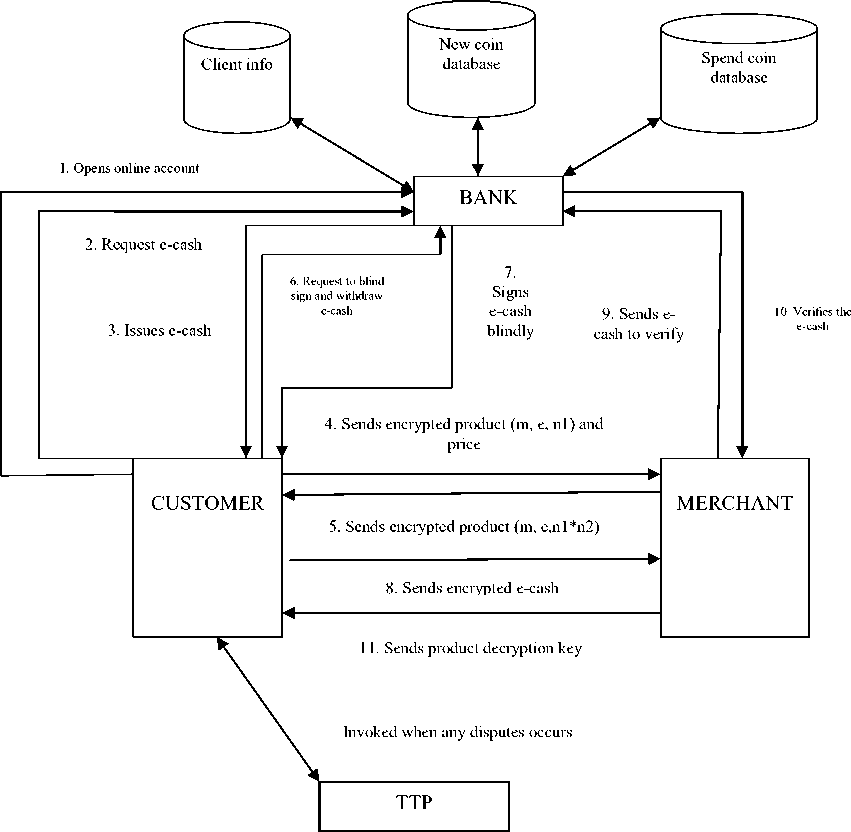
Fig.1. Block Diagram of Protocol

The working of each phase is describes in below steps:

• 1) . Initial Setup

First of all bank, merchant and TTP gets their public key certificate from the CA (for this we assumed that they already have applied to CA) and publish their public key online and keeps their private key separately with them. Merchant also gets the product certificate from TTP. For this he registers the product with TTP whereas TTP calculates different product key for each product i.e. public and private key pair using RSA algorithm and encrypt the product with public key which is denoted by (e, n1) and publish on website. Now the product which is seen by customer is in encrypted form (m, e, n1) along with its cost and name. Merchant also calculates the compatible public private key pair for that product which is represented as (e, n2) and (d2, n2) and keeps keys with him. Table 1 describes various notations used in our protocol.

• 2) . Registration Phase

In registration phase, for signing message we used asymmetric key because customer do not have any public and private key pair. For asymmetric key encryption we used AES-128.

^Ьтгк_е (us е п _d + t im e_customer + s e cere __k ey + ^ ^p ass w о r d _ cu s t(H(msg)) (1)

In eq. 1, customer first of all opens online bank account by entering user-id and password which was given earlier by bank and chooses security which later acts as asymmetric key.

• 3) . Issuing E-cash

  We have used online system for storing e-cash rather than using e-wallet concept. For issuing e-cash first of all customer login into the online e-cash bank and apply for e-cash than bank gives the e-cash by generating some random serial coin like “191043011281012345”. In this representation of coin 191 is bank number, 0430 coin creation date, 112810 (“mmss”) is coin creation time and

  12345 is random serial number which issued to customer coin database of bank. and hash of e-cash with its expiry date is stored in new

Table 1. Notations used in Protocol

Symbol	Description
EK	Encrypted using asymmetric key
E(msg)	E stands for encryption using public key
^bank _ , ^merchant _ ,     _	bank public key, merchant public key and TTP public key
user(cl	User identification basically customer id
_	Password of customer
H(msg)	Hash of message using hash algorithm
tiTnecllstomer , ИтеЬш1к , ti-memeTCiv , timettp	Time of customer, merchant, TTP and bank
^merchant _ d , ^bank _ d , Ettp _	Merchant, bank and TTP private key
(m, e, n1*n2)	Message m is encrypted with compatible public key
_       _	Customer temporary private key
_ ,            _	Customer temporary public key for each transaction

• 4) . Withdrawal Phase

In this phase, before sending withdrawal request to bank customer first creates trust between merchant and himself by sending encrypted product and cost to merchant and takes merchant signs on encrypted product. In eq. 2, customer first of all creates temporary private public key pair (note that this is temporary key pair for each transaction) to hides its true identity because temporary key pair does not contains any information of customer and sends to merchant along with cost and encrypted product.

• i)

Customer ----► Merchant

E-merchant_e ( time customer +( m , e , n 1)+ temp_e + temp_n + product_cost +      _   _ ( H ( msg ))) (2)

Eq. 2 contains:

• 1 .) (m, e, n1) encrypted product details

• 2 .) Timestamp for avoiding replay attack.

• 3 .)       _    _ ( H ( msg )) Signed message using

customer temporary private key pair.

• ii)

Merchant ____N Customer

Merchant decrypts eq. 2 by its private key and checks whether all details regarding product is correct or not. Merchant also checks digital signature and timestamp of message is correct. If all the details are correct than merchant sends product encrypted with compatible key along with its signature on it to customer.

custtempe ((m,e,n1∗n2)+ time customer + time mer chant +SlgTLmeT chant (m,e,n1∗ n2)+Emerchant^ (H( msg)))         (3)

• iii)

Customer ----► Bank

Now, after receiving eq. 3 customers checks the sign of merchant on product and also checks price of product with sending price. After getting trust on merchant customer sends e-cash withdrawal request to bank and sends hash value of actual e-cash with blinded e-cash because to maintain customer anonymity from bank customer sends blinded e-cash. Blinded e-cash contains ( ecas ℎ xor amount ) because later bank will able to verify both e-cash and amount.

^bank ( user_td + Has һ ( ecas һ)+ blinded, ecas ℎ+ amount +          _   ( H ( msg )))       (4)

• iv)

  

After receiving eq. 4, bank first checks whether hash of e-cash present in new coin database or not. If it present in new coin database than bank comes let to know that customer is genuine and sends signed e-cash to customer.

^^security к_еу ( user_id + signed - ecas ℎ+

Ebank _ cl ⁽ H ⁽ msg )))                (5)

_

After receiving eq. 5, customers first decrypts message by using its own symmetric security key then checks bank signature on message and gets the signed e-cash by removing its blinding factor.

Now representation of e-cash coin will be (( ecas ℎ xor amount ) ^dbmodn , e-cash, amount) this will be send to the merchant.

• 5) . Payment and Deposit Phase

In this phase, customer sends e-cash, encrypted product and sign of merchant on encrypted product to merchant.

Here, e-cash is again encrypted with bank’s public key so that merchant is not able to see it. The message will be in form of eq. 6.

i.)

Customer ____^ Merchant

^merchant (( m , e , n 1∗ n 2)+ time customer +

SiQ^merchant ( m , e , n 1∗ n 2)+ encrypted, ecas һ+

_    _ ( H ( msg )))              (6)

After receiving information from customer, merchant sends encrypted e-cash, product cost, his own account number and a unique transaction-id to bank.

• ii)

Merchant ----► Bank

Ebank_e ( encrypted ecas һ+ COS t_oy р_ТОд_ис^ + tiTYie_merCh,a,Tit + UCCOUTlt_no + transcationi_d +

^merchant _ й ( H ( msg )))              (7)

—

After receiving message from merchant bank, first of all decrypts encrypted e-cash with his own private key than checks his signature on (e-cash xor amount). If everything is alright than also verifies e-cash amount with cost of product and checks the specified e-cash number has already been spent before or not. After checking double spender, bank credits genuine merchant account with appropriate amount.

• iii)

Merchant ----► Customer

After receiving transaction successful message from bank genuine merchant will sends product decryption key to his customer along with unique transaction id in form of eq. 8.

• 6) . Dispute Algorithm

For achieving fair exchange we used off-line TTP model in which merchant has to registers their products first with TTP before publishing on web. As we have seen that before start of transaction customer obtained merchant signature on encrypted product this will leads to maintain trust between customer and merchant but in worst cases it can be possible that merchant cheat’s customer. There are two ways in which merchant can cheats customer:-

Case 1: Merchant do not sends product key after receiving payment.

Case 2: Merchant sends incorrect product key after receiving payment.

Here we implemented the case 2 for this protocol. But there will be less chances of dispute occurrence because at time of trust building customer first gets merchant signature on encrypted product so the genuine merchant never do cheating because customer can sends the signed message to TTP for taking some action against merchant. The steps of dispute algorithm are given as below:

• i)

Customer ____*. TTP

In this step, customer sends all the information regarding merchant, e-cash and product to TTP after getting wrong product from merchant.

^ttp_e ( encrypted ecas h+ time customer + mer h CCLTltid +( m , e , n 1∗ n 2)+

Sl^Tlmerchant ( m , e , n 1∗ n 2)+ temp_e + temp_n + transaction _ id +      _    _ ( H ( msg )))    (9)

• ii)

TTP ---► Bank

Now, after receiving eq. 9 from customer bank sends ecash to bank for knowing that whether this e-cash is already been spent or not because it may be possible that fake customer built a random string and sends to TTP and claims that merchant didn’t send right product.

^bank_e ( encrypted ecas һ+ time_ttp + Ettp_d ( H ( msg )))               (10)

• iii)

TTP ----► Merchant

After getting a good acknowledgement from bank that customer is fair this e-cash is already spent, TTP sends following information to merchant and starts a timer that merchant have to respond on that time otherwise TTP will take an appropriate action against it.

Emerchant_e (( m , e , n 1∗ n 2)+ time^p +

^iS^merchant ( m , e , n 1∗ n 2)+ trnasaction_id + _ ( H ( msg )))               (11)

iv)

Merchant ____► TTP

If merchant responds in time then the TTP receives eq. 12 otherwise TTP receives “0” message.

Merchant to TTP, timer expires message=”0”;

Or

E_ttp _e (P r о duc t_{de cryp 1to n}key + t im e_ttp + ti ^m e_{m e тс} ^ an t + E_meTcdan t_^ ⁽H⁽ms g )))

v)

TTP ----► Customer

In last step of this algorithm if merchant did not sends any product decryption key to TTP, TTP will sends product key from his own database to customer and takes some appropriate action against merchant.

Ecus 11emp e (pro duc td eCyyp 110 nkey + t im ccustomer + timet tp + Et tp _d(H(msg))          (13)

• V.    Experiment Result and Analysis

We have developed our protocol in java using socket programming. We have also performed an experiment over four systems which acts as customer, bank, merchant and TTP. Later, in this section we analyzed performance of our protocol with on-line TTP protocol. First of all customer need to open his online account in respective bank and issues e-cash as shown in fig. 2.

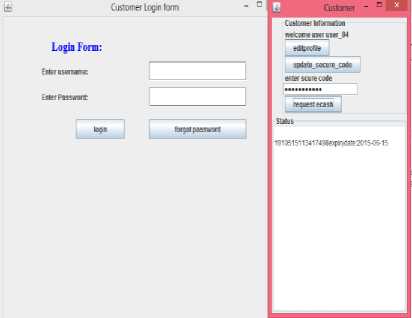
Fig.2. Issue of E-cash

Merchant_store [ J ava Applic ation] C :\Program F iles\java\bin\j avaw. exe

Receiver activated and has been connected to server

Merchant IP address/10.20.131.12. at port 7743

Connected to merchant

Customer making anonymous identity and sending encrypted message to merchant

Msg: 702437778041651652643434672671926473674635463546534635613

Time of sending message is: 2015-05-15 + 10:58:51

Customer gets encrypted product from merchant using (m,e,nl*n2)

Customer verifying product sign,

06e5ab99c975d8cb7b374b7fb8127382e383783

Customer sending and receiving time has been verified

Fig.3. Customer Sends and Receives Encrypted Product to and from Merchant

After issuing of e-cash, customer goes to online merchant store and selects a product after selecting product customer sends eq. 2 to merchant in encrypted form and receives eq. 3 shown in fig. 3.

After receiving a trust factor and signature from merchant on product, customers sends withdrawal request to bank in fig. 4. We have also used OTP (one time password) for customer authentication. Customer blinds the actual value of e-cash and sends hash of e-cash to bank so that bank can be able to check that this e-cash is already been spent before or not.

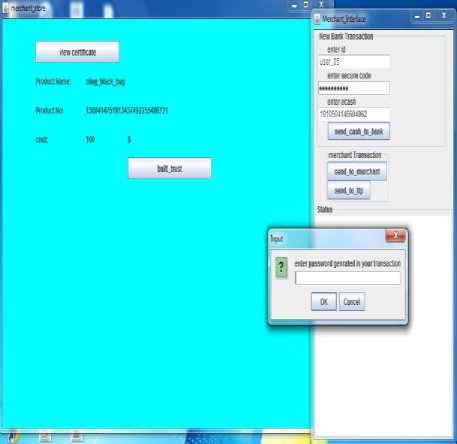
Fig.4. Customer Fills Withdrawal Sends E-Cash Withdrawal Request to Bank

After receiving withdrawal request, bank will sends signed blinded e-cash to customer and debits respective amount from customer account. The bank operation is shown in fig. 5.

Preparing for sending

Connected to customer

Bank activated and has been connected to customer

Customer IP address /10.20.131.10

Bank getting message or blinding factor..

Encrypted message is

361315792328836675992039163163351095044927136609#! 6207665468338#vArMqpiM+6namFtPHq xQ8F7Dhz8NoE=

Hash of e-cash is : O5476f94aecd4c8c86aa446573fb5576a8ac772172b889f7ab59aaab6fca4439

Authorized user

Verified hash

Bank is sending otp dtp sending time is: 2015-05-15+10:59:39

Verified OTP

OTP has not been expired

User amount is updated

User_history is updated

Bank sending blinded e-cash to customer using coin private_key

262062507237421165136667263557515253840232898419493871077193048641542425561588804764 391

Message sending time is : 2015-05-15+10:59:47

Preparing for sending

Fig.5. Bank Sends Blinded E-cash to Customer

After receiving signed blinded e-cash customer removes blind factor ‘r’ and again encrypts e-cash with bank’s public key and sends eq. 6 to merchant

After receiving signed blinded e-cash customer removes blind factor ‘r’ and again encrypts e-cash with bank’s public key and sends eq. 6 to merchant.

After receiving e-cash from customer merchant sends them to bank for crediting his own account and later sends correct product key to customer which shown in fig.6. If in any case, customer receives wrong product than customer invokes dispute algorithm in which customer sends all the details regarding merchant and product to TTP than TTP will forwards the details to bank for knowing whether customer is playing fair or not.

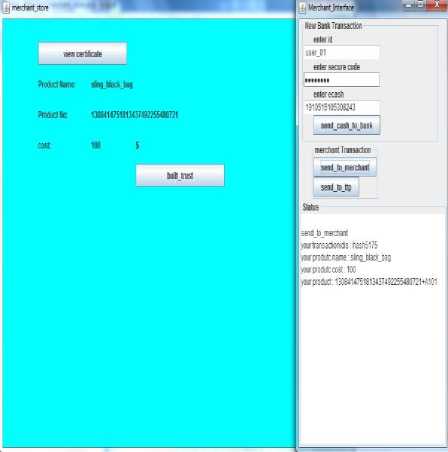
Fig.6. Customer Receives Correct Product from Merchant

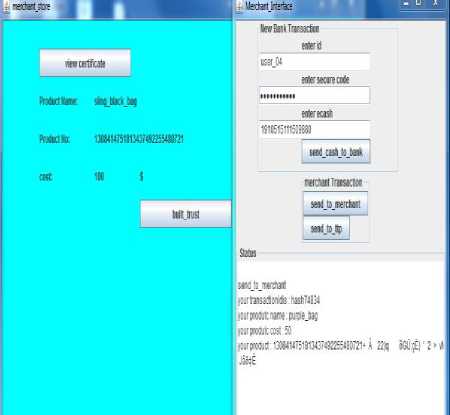
Fig.7. Customer Receives Incorrect Product Details

After getting acknowledgement from bank TTP forwards message to merchant and waits till merchant reply. Fig. 7 shows that customer receives incorrect product which is different from the product which was requested by customer. Fig. 8 shows that TTP starts a timer and merchant didn’t response in that time then TTP forwards correct product key from his database to customer.

We have also analyzed our protocol in terms of time by calculating time of each phase shown in fig. 9. The performance of system is good enough even with increase in the number of users. We calculated the time of each phase up to 8 customers which request to buy a product using on-line e-cash protocol. Basically, the time of withdrawal phase is more than two phases i.e. deposit and payment phases, because in withdrawal phase time depends upon time to enter one time password. The time also depends upon how much crypto operations applied on each phase of protocol.

Preparing for sending

Connected to customer

TTp activated and has been connected to customer

Customer IP address/10.20.131.10 at port 6691

Message from customer

TTP sending E-cash to bank for checking

TTP connected to bank

Waiting to connect

Connected to bank

Client: 1

Message comes from bank 1

Customer is fair

Merchant IP address/10.20.131.12 at port no 7773

Waiting to connect

Connected to merchant

Sender: waiting for message from merchant

Message is: 0

Terminating merchant not respond times out

TTP sending message to customer

Preparing for sending

Fig.8. Merchant Didn’t Response in Given Time and Timeout Error Occurs

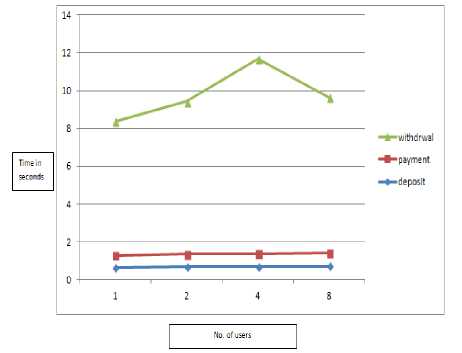
Fig.9. Time Calculation Graph

We calculated difference of our protocol with online TTP protocol in terms of time taken in payment phase and it shows that our protocol gives better result than online TTP protocol. Fig.10. shows the timing difference of payment phase.

We also compared our offline TTP protocol with online TTP e-cash protocol in which there is no direct contact between merchant and customer takes place.

In online TTP protocol there is no use of making compatible keys because customer is not going to make direct communication with merchant. By using online TTP there is guarantee of fair exchange but sometime TTP will becomes a bottleneck problem.

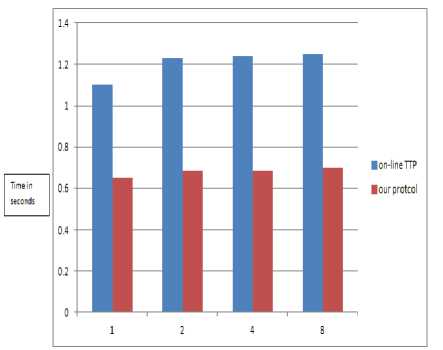
No. of users

Fig.10. Time Calculation Graph of Payment Phase

Some researchers [11] [23] also proposed online e-cash protocol but their protocol have still some weakness. In table 2, we compare our protocol with some already proposed e-cash protocols.

Table 2. Comparison between Song, Swe and Our Protocol

Song	Swe	Proposed protocol
Customer    uses asymmetric cryptography   in withdrawing phase	Customer     uses asymmetric cryptography     in withdrawing phase	Author uses hybrid cryptography (symmetric    with asymmetric)     in withdrawing phase
Protocol fail to provide fair exchange	Improvement over song protocol but while providing fair exchange anonymity of customer breaches	Provides anonymity and fair exchange to customer.

• VI.    Conclusion

In this paper, we worked on on-line e-cash protocol which acts as online payment method. Basically e-cash is in the form of some strings or bits and should be anonymous in nature. For achieving anonymity we used blind signature. The protocol ensures all the features of cryptography by using public key as well as private key cryptography. For fair exchanging of online products we used offline TTP. The protocol is also sufficient against replay attacks and we used the concept of OTP for achieving authentication of user. Even at login time of customer on bank timestamp also gets attached along with user-id and password so that if any attacker traces the sent message and later sends it to bank than attack can be detected by receiving parties. By using on-line e-cash protocol user can be able to do transaction from any location which makes it more users friendly.

We also performed an experiment on four systems and also calculated the timing difference of each phase and it shows that even with increase in number of user protocol takes less time than on-line TTP protocol.

The protocol can be enhanced by fixing e-cash value to some denomination earlier. The bank and TTP also acts as one server rather than using two different servers.