Improved Apriori Algorithm for Mining Association Rules

Published Online June 2014 in MECS

• A.    Basic Concepts

Many business enterprises accumulate large quantities of data from their day to day operations. For example, huge amounts of customer purchase data are collected daily at the checkout counters of grocery stores. Table 1 illustrates an example of such data, commonly known as market basket transactions. Each row in this table corresponds to a transaction, which contains a unique identifier labeled TID and a set of items bought by a given customer. Retailers are interested in analyzing the data to learn about the purchasing behavior of their customers. Such valuable information can be used to support a variety of business-related applications such as marketing promotions, inventory management, and customer relationship management.

Association analysis is useful for discovering interesting relationships hidden in large data sets [1]. The uncovered relationships can be represented in the form of association rules or sets of frequent items. The following rule can be extracted from the data set shown in Table 1:

{Diapers} ^ {Beer}

Table 1. An example of market basket transactions

TID	Items
1	{Bread, Milk}
2	{Bread, Diapers, Beer, Eggs}
3	{Milk, Diapers, Beer, Cola}
4	{Bread, Milk, Diapers, Beer}
5	{Bread, Milk, Diapers, Cola}

The rule suggests that a strong relationship exists between the sale of diapers and beer because many customers who buy diapers also buy beer. Retailers can use this type of rules to help them identify new opportunities for cross selling their products to the customers.

Besides market basket data, association analysis is also applicable to other application domains such as bioinformatics, medical diagnosis, Web mining, and scientific data analysis. In the analysis of Earth science data, for example, the association patterns may reveal interesting connections among the ocean, land, and atmospheric processes. Such information may help Earth scientists develop a better understanding of how the different elements of the Earth system interact with each other [2] [3].

• B.    Itemset and Support Count

Let I = {i1, i2. . . id} be the set of all items in a market basket data and T = {t1, t2. . . tN} be the set of all transactions. Each transaction ti contains a subset of items chosen from I. In association analysis, a collection of zero or more items is termed an itemset. If an itemset contains k items, it is called a k-itemset. The null set is an itemset that does not contain any items.

The transaction width is defined as the number of items present in a transaction. A transaction tj is said to contain an itemset X if X is a subset of tj. An important property of an itemset is its support count, which refers to the number of transactions that contain a particular itemset.

• C.    Association Rule

An association rule is an implication expression of the form X ^ Y , where X and Y are disjoint itemsets, i.e.,

X ∩ Y = ∅. The strength of an association rule can be measured in terms of its support and confidence. Support determines how often a rule is applicable to a given data set, while confidence determines how frequently items in Y appear in transactions that contain X. The formal definitions of these metrics are

Support, s(X → Y) = ^{σ ( XY )}

N

Confidence, c(X → Y) = ^σ ( ^XY ) σ ( X )

• D.    Support and Confidence

Support is an important measure because a rule that has very low support may occur simply by chance. A low support rule is also likely to be uninteresting from a business perspective because it may not be profitable to promote items that customers seldom buy together. Support is often used to eliminate uninteresting rules. Support has a desirable property that can be exploited for the efficient discovery of association rules.

Confidence measures the reliability of the inference made by a rule. For a given rule X → Y , the higher the confidence, the more likely it is for Y to be present in transactions that contain X. Confidence also provides an estimate of the conditional probability of Y given X.

• E.    Frequent Itemset Generation

A lattice structure can be used to enumerate the list of all possible itemsets. In general, a data set that contains k items can potentially generate up to 2 ^K -1 frequent itemsets, excluding the null set. Because k can be very large in many practical applications, the search space of itemsets that need to be explored is exponentially large.

A brute-force approach for finding frequent itemsets is to determine the support count for every candidate itemset in the lattice structure. To do this, we need to compare each candidate against every transaction, an operation that is shown in Fig. 1. If the candidate is contained in a transaction, its support count will be incremented. Such an approach can be very expensive because it requires O (NMw) comparisons, where N is the number of transactions, m = 2 ^K -1 is the number of candidate itemsets, and w is the maximum transaction width.

N

ТО 1 2 3 4 5

Transactions

___________ Items _______ Bread. Milk _______________ Bread. Diapers. Beer, Eggs Milk. Diapers, Beer Coke Bread. Milk, Diapers. Beer Bread. Milk, Diapers. Coke

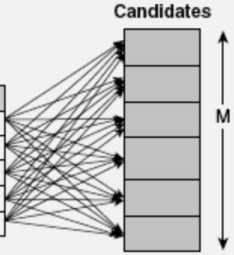
Fig 1. Counting the support of candidate itemsets

There are several ways to reduce the computational complexity of frequent itemset generation.

• 1)    Reduce the number of candidate itemsets (M). The

Apriori principle, described in the next section, is an effective way to eliminate some of the candidate itemsets without counting their support values.

• 2)    Reduce the number of comparisons. Instead of matching each candidate itemset against every transaction, we can reduce the number of comparisons by using more advanced data structures, either to store the candidate itemsets or to compress the data set.

• II.    The Apriori Principle

Support measure helps to reduce the number of candidate itemsets explored during frequent itemset generation. The use of support for pruning candidate itemsets is guided by the Apriori Principle. “If an itemset is frequent, then all of its subsets must also be frequent.” Considering the itemset lattice shown in Fig. 2, suppose {c, d, e} is a frequent itemset. Any transaction that contains {c, d, e} must also contain its subsets, {c, d}, {c, e}, {d, e}, {c}, {d}, and {e}. As a result, if {c, d, e} is frequent, then all subsets of {c, d, e} must also be frequent [6].

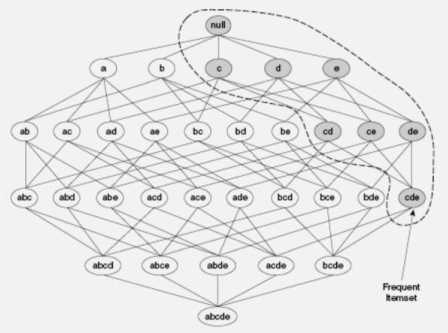
Fig. 2. An illustration of the Apriori principle

Conversely, if an itemset such as {a, b} is infrequent, then all of its supersets must be infrequent too. As illustrated in Fig. 3, the entire sub graph containing the supersets of {a, b} can be pruned immediately once {a, b} is found to be infrequent. This strategy of trimming the exponential search space based on the support measure is known as support-based pruning. Such a pruning strategy is made possible by a key property of the support measure, namely, that the support for an itemset never exceeds the support for its subsets. This property is also known as the anti-monotone property of the support measure.

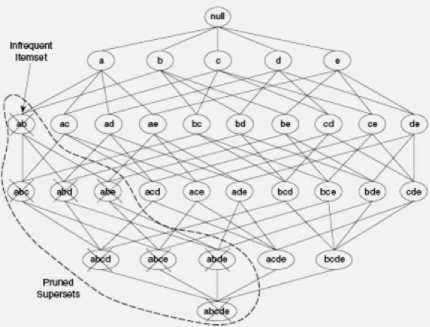
Fig. 3. An illustration of support-based pruning

Any measure that possesses an anti-monotone property can be incorporated directly into the mining algorithm to effectively prune the exponential search space of candidate itemsets.

• A. Frequent Itemset Generation in the Apriori

Algorithm

Apriori is the first association rule mining algorithm that pioneered the use of support-based pruning to systematically control the exponential growth of candidate itemsets. Fig. 4 provides a high-level illustration of the frequent itemset generation part of the Apriori algorithm for the transactions shown in Table 1. Considering the support threshold is 60%, which is equivalent to a minimum support count equal to 3.

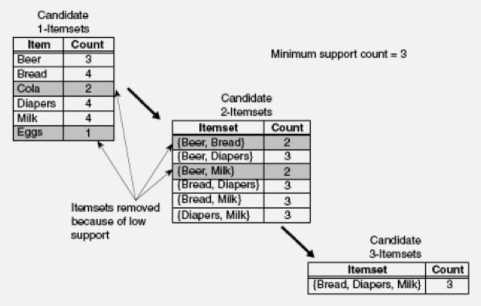
Fig. 4. Illustration of frequent itemset generation using the Apriori algorithm

Initially, every item is considered as a candidate 1-itemset. After counting their supports, the candidate itemsets {Cola} and {Eggs} are discarded because they appear in fewer than three transactions. In the next iteration, candidate 2-itemsets are generated using only the frequent 1-itemsets because the Apriori principle ensures that all supersets of the infrequent 1-itemsets must be infrequent. Because there are only four frequent 1-itemsets, the number of candidate 2-itemsets generated by the algorithm is | 4 | = 6. Two of these six candidates, 12 )

{Beer, Bread} and {Beer, Milk}, are subsequently found to be infrequent after computing their support values. The remaining four candidates are frequent, and thus will be used to generate candidate 3-itemsets. Without supportbased pruning, there are | 6 | = 20 candidate 3-itemsets 1 3 )

that can be formed using the six items. With the Apriori principle, we only need to keep candidate 3-itemsets whose subsets are frequent. The only candidate that has this property is {Bread, Diapers, Milk}.

The effectiveness of the Apriori pruning strategy can be shown by counting the number of candidate itemsets generated. A brute-force strategy of enumerating all itemsets (up to size 3) as candidates will produce

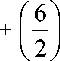
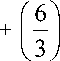
= 6 + 15 + 20 = 41

candidates. With the Apriori principle, this number decreases to

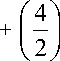
+ 1 = 6 + 6 + 1 = 13

candidates, which represents a 68% reduction in the number of candidate itemsets. The pseudo code for the frequent itemset generation part of the Apriori algorithm is shown below.

Apriori algorithm for frequent itemset generation

• 1.    k = 1

• 2.    Fk =   {i | i e I л су ({i}) ^ N x min sup}

• 3.    repeat

• 4.           k = k +1

• 5.             C_k = apriori-gen (F_k_j) {Generate

• 6.            for each transaction t e T do

• 7.                        C_t    = subset (C_k, t)

• 8.                      for each candidate itemset

9.                    у (c ) = у ( c ) +1

• 10.                    end for
  
  11.           end for

• 12.            Fk =     {c | c e C_k л o(c)>Nx min sup}

• 13.    until Fk = 0

• 14.    Result = F

{Find all frequent 1-itemsets}

candidate itemsets}

{Identify all candidates that belong to t}

c e Ct do

{Increment support count}

{Extract the frequent k-itemsets}

Procedure apriori_gen ( F )

• 1.    for each itemsets f 1 E F k _ 1 do

• 2.            for each itemsets f₂ E F_k__x do

• 3.                  if ( f , [ 1 ] = f 2 [ 1 ] ) Л

• 4.                        c = f ® f 2

• 5.                             for each ( k — 1 )-

• subsets s of c do

(f1 [2] = f2 [2]) л ... л (fl[k _ 2] = f2 [k _ 2])

л ( f [ k _ 1 ] = f [ k _ 1 ] ) then

{join step: generate candidates}

• 6-                                               ^{if (s} 6 fk _ 1 )

• 7.                                   delete c

• 8.                                              else

• 9.                               add c to C_k

• 10.                            end for

• 11.                           return C

• 12.               end if

• 13.           end for

• 14.    end for

then

{prune step: remove candidates}

Procedure subset ( C , t)

• 1.    for all candidates s E C_k do

• 2.               if t contains s

• 3.                 subset = subset + { s }

• 4.    end for

C denote the set of candidate k-itemsets and F denote the set of frequent k-itemsets:

• •    The algorithm initially makes a single pass over the data set to determine the support of each item. Upon completion of this step, the set of all frequent 1-itemsets F will be known (steps 1 and 2).

• •    Next, the algorithm will iteratively generate new candidate k-itemsets using the frequent (k - 1)-

• itemsets found in the previous iteration (step 5). Candidate generation is implemented using a function called apriorigen.

• •    To count the support of the candidates, the algorithm needs to make an additional pass over the data set (steps 6–10). The subset function is used to determine all the candidate itemsets in C that are contained in each transaction t.

• •    After counting their supports, the algorithm eliminates all candidate itemsets whose support counts are less than minsup (step 12).

• •    The algorithm terminates when there are no new frequent itemsets generated, i.e., F_K = Ф (step 13).

The frequent itemset generation part of the Apriori algorithm has two important characteristics.

• 1)    First, it is a level-wise algorithm; i.e., it traverses the itemset lattice one level at a time, from frequent 1-itemsets to the maximum size of frequent itemsets.

• 2)    Second, it employs a generate-and-test strategy for finding frequent itemsets. At each iteration, new candidate itemsets are generated from the frequent itemsets found in the previous iteration. The support for each candidate is then counted and tested against the minsup threshold. The total number of iterations needed by the algorithm is K_{ma x} +1, where K _max is the maximum size of the frequent itemsets.

• B.    Candidate Generation and Pruning

The apriori-gen function shown in Step 5 of algorithm generates candidate itemsets by performing the following two operations:

• 1)    Candidate Generation: This operation generates new candidate k-itemsets based on the frequent (k - 1) -itemsets found in the previous iteration.

• 2)    Candidate Pruning: This operation eliminates some of the candidate k-itemsets using the support-based pruning strategy.

Considering a candidate k-itemset, X = { i i      i }, the algorithm must determine whether all of its proper subsets, X - {ij } (Vy. = 1, 2, . . . ,k), are frequent. If one of them is infrequent, then X is immediately pruned. This approach can effectively reduce the number of candidate itemsets considered during support counting. The complexity of this operation is O (k) for each candidate k-itemset [6] [7].

In principle, there are many ways to generate candidate itemsets. The following is a list of requirements for an effective candidate generation procedure:

• 1)    It should avoid generating too many unnecessary candidates. A candidate itemset is unnecessary if at least one of its subsets is infrequent. Such a candidate is guaranteed to be infrequent according to the antimonotone property of support.

• 2)    It must ensure that the candidate set is complete, i.e., no frequent itemsets are left out by the candidate generation procedure. To ensure completeness, the set of candidate itemsets must subsume the set of all frequent itemsets.

• 3)    It should not generate the same candidate itemset more than once. Generation of duplicate candidates leads to wasted computations and thus should be avoided for efficiency reasons.

• III.   Proposed Algorithm For Mining

Association Rules

• A.    Enhancement of Subset Procedure

13.             C       =     apriori-gen

{Generate candidate itemsets}

( L k - . )

• 14.            for each transaction t e T do

• 15.                      C_t = subset ( C_k , t )

{Identify all candidates that belong to t}

16.                     for each candidate

c e C_t do

itemset

17.                           о ( c ) — о ( c ) + 1

{Increment support count}

• 18.                     end for

• 19.             end for

²0.             ^L k ^—    { c | c e C_k л о ( c ) > N x minsup }

{Extract the frequent k-itemsets}

• 21.    until L k — 0

• 22.    Result =   L

Procedure subset ( C_k , t)

1.	for all candidates s e C do
2.	if t contains s
3.	subset = subset + { s }
4.	end for

Improved Procedure subset ( C , t)

1.	for all candidates s e C k do
2.	If (first item of s > min ) Q (last item of
s <  max )
3.	subset = subset + { s }
4.	end for

Its running time is o ( | D | ^k ) , this is a very large number. Considering k = 3, the transaction t (x2, x6, x7, x9), the itemsets s (x4, x6, x10). Refinement of this sentence: “if t contain s during a judge are the following conditions: if (t contains x4)     (t contains x6)     (t contains x10)

then…..” Obviously, t does not contain s, but still have to compare one by one [8].

The proposed algorithm improves the subset operation through adding a tag column on the transaction database, of which values are the first and the last numbers of itemsets. If (first item of x > = min) (last item of x <= max), then t contains s. Otherwise t does not contain s.

• B.    Proposed Apriori Algorithm

The Proposed algorithm can be divided into two steps. First, the algorithm finds out all frequent itemsets. Then it generates all association rules from frequent itemsets.

Input: A database D and min-support

Output: All the frequent itemsets of the database

• 1.    k — 1

• 2.     ^Lk —    {i | i e I л о ({i}) > N x min sup}

3.    C — L ® L 4.    for all candidates c e C2 do 5.              Ct = subset ( C2, t) 6.             for all candidates C e Ct do 7.                    о ( c ) — о ( c ) +1 8.             end for 9.    L2 — {c | c e Ck л о (c)> N x min sup} 10.   end for 11.   repeat 12.           k — 3

{Find all frequent 1-itemsets}

As C is connected by L and pruning two-generated, of which pruning operations to test whether a subset of C ₂ is frequent itemsets. Because C ₂ — L ® L , the subset of the set must be frequent. Therefore, the proposed algorithm generates C by the direct connection of L , rather than by pruning operation [14] [17].

• IV.    Working Of Proposed Algorithm

Table 2. Transactional Database D

Transaction No.	Itemsets
T100	I1, I2, I5
T200	I2, I4
T300	I2, I3
T400	I1, I2, I4
T500	I1, I3
T600	I2, I3
T700	I1, I3
T800	I1, I2, I3, I5
T900	I1, I2, I3

Table 3. The Database in the proposed algorithm

Transaction No.	Itemsets	Tag
T100	I1, I2, I5	1, 5
T200	I2, I4	2, 4
T300	I2, I3	2, 3
T400	I1, I2, I4	1, 2, 4
T500	I1, I3	1, 3
T600	I2, I3	2, 3
T700	I1, I3	1, 3
T800	I1, I2, I3, I5	1, 2, 3, 5
T900	I1, I2, I3	1, 2, 3

The first to deal with a database in the form of Table 3, the last one marked with the corresponding transaction of the smallest item serial number and the largest serial number. After the first scan the database, looking for L , you can compare the various tag of the transaction, because L is not in [2, 4], or in [2, 3], and so on to avoid many comparison of the operation and thereby saving time.

After calculating support, L = {I1, I2, I3, I4, I5}. According to the improved algorithm, C connected directly by L is no need for pruning operations. Thus, C 2 = {(I1, I2), (I1, I3), (I1, I4), (I1, I5), (I2, I3), (I2, I4), (I2, I5), (I3, I4), (I3, I5), (I4, I5)}. As (I1, I2) in [1, 5], it includes the transaction T100 and increases the corresponding support. And so on, L = {(I1, I2), (I1, I3), (I1, I5), (I2, I3), (I2, I4), (I2, I5)}. After pruning after connecting C = {(I1, I2, I3), (I1, I2, I5)}. Itemsets (I1, I2, I3) in [1, 5], and so increases in support. Because it is not in [2, 4] or [2, 3] and therefore do not increase support. Finally, L = {(I1, I2, I3), (I1, I2, I5)}. C can not be find as the algorithm end. Clearly, the proposed algorithm reduces the number of unnecessary operations, streamline the collection of frequent generation and improve the efficiency of the algorithm.

• V.    Implementation

• A.    Class File Detail

• 1)    Apriori.cs

It contains class and methods used to implement the APriori Market Based Analysis Data Mining Algorithm. Apriori class implements the APriori algorithm for market based analysis. This class implements the APriori algorithm and creates association between items in a transaction.

• 2)    DataAccessLayer.cs

Implements data access to relational databases and XML data stores.

• 3)    DataMining.cs

• 4)    Itemsets.cs

An abstract class that represents a set items from a shopping cart. Defines the Level of an Itemset, its Items and Support Count. The level of an Itemset is the Hierarchy of an itemset or how many items make up the Itemset. A one level Itemset contains one item. A two level Itemset contains two items.

• 5)    DataTransformationServices.cs

• B.    Screen Shots

  

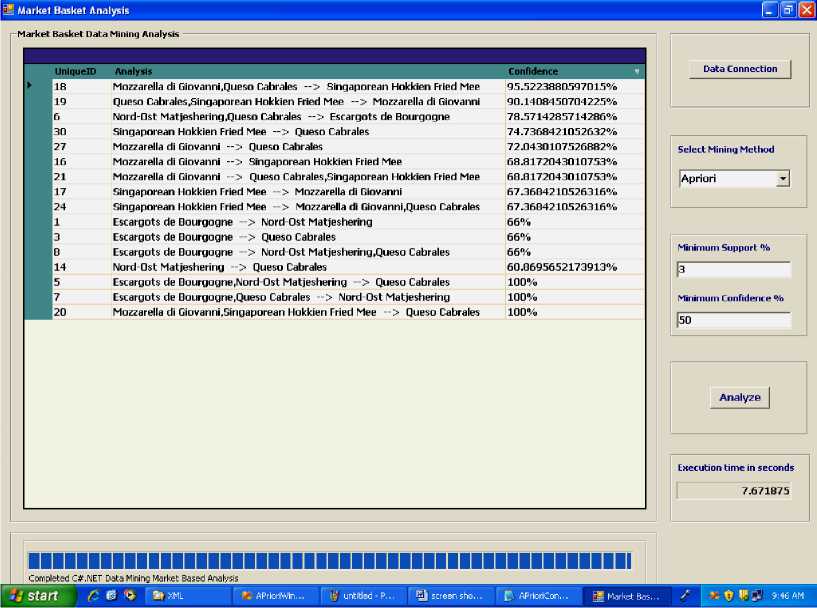
  Fig. 5. Output of application using Apriori algorithm

  
  
  

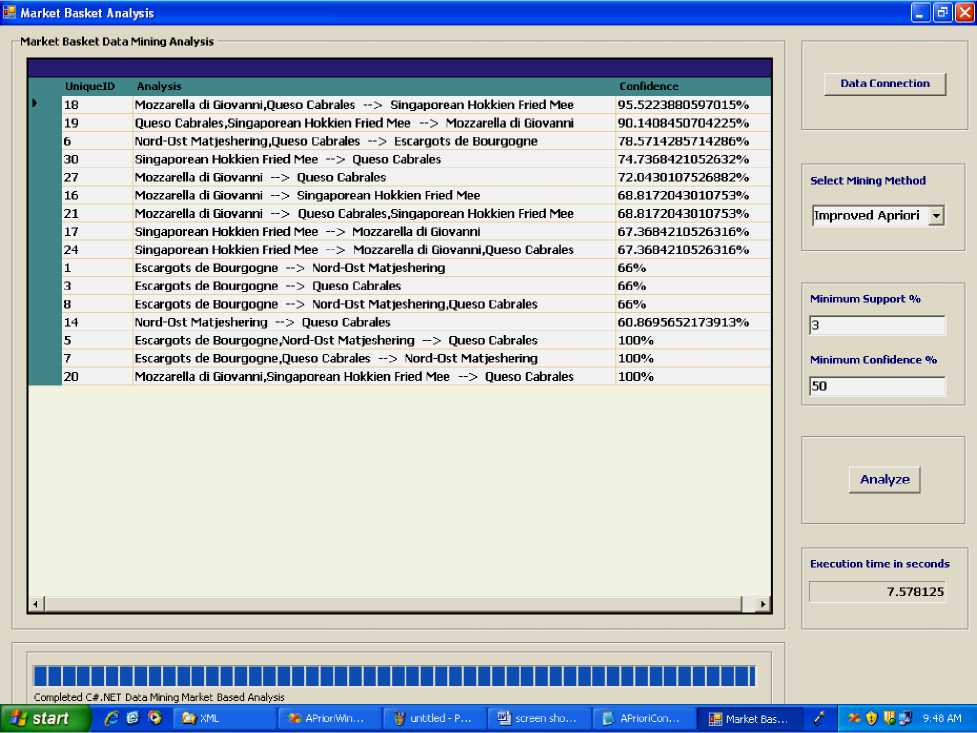
  Fig. 6. Output of application using Improved Apriori algorithm

  
  

• VI.    Performance Study

  In order to study the performance, the computer used to run the experiments had Intel(R) Pentium D CPU 2.80 GHz processor and 512 MB of memory and 512 MB of memory. The operating system used was Microsoft Windows XP Professional. Programs are coded in C#.NET on the platform of Visual Studio 2005. The performance of the Apriori algorithm is largely depends on the internal characteristic of the datasets and the number of records. To make the time measurements more reliable, no other application was running on the machine while the experiments were running.

Algorithm has been tested on the three different datasets described in the previous chapter. The performance measure is the execution time (seconds) of the algorithms on the datasets. The minimum confidence is set to 50%.

Table 4. Dataset characteristics

Datasets	Transactions	Distinct Items	Maximum Transaction Size	Average Transaction Size
Retail Sales	5000	200	8	3.0
Adventure Works	15000	500	12	5.0

A. Experimental Analysis

• (1)    Retail Sales Dataset

Table 5. The comparison of the runtime at different minimum support between the Apriori algorithm and the Improved Apriori algorithm

Minimum Support (%)	Execution Time (Seconds)		Rule Count
	Apriori	Improved Apriori
1	8.42	8.29	23
2	8.21	8.14	23
3	8.21	8.15	23
4	7.92	7.71	17
5	7.65	7.65	16
6	7.90	7.65	16
7	7.75	7.65	16
8	7.35	7.21	10
9	7.14	6.81	3
10	6.76	6.68	0

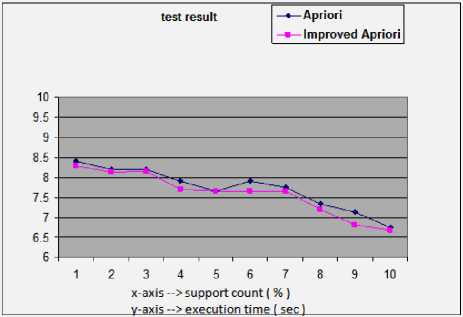
Fig. 7. The comparison of runtime at different minimum supports between the original Apriori and the improved Apriori

• (2)    Adventure Works Dataset

Table 6. The comparison of the runtime at different minimum support between the Apriori algorithm and the Improved Apriori algorithm

Minimum Support (%)	Execution Time (Seconds)		Rule Count
	Apriori	Improved Apriori
10	534.67	533.54	1024
15	242.78	241.92	817
20	87.73	87.41	321
25	56.14	55.94	50
30	53.15	52.97	9
35	52.48	52.34	2
40	53.45	52.23	0
45	53.09	53.00	0
50	52.35	52.25	0

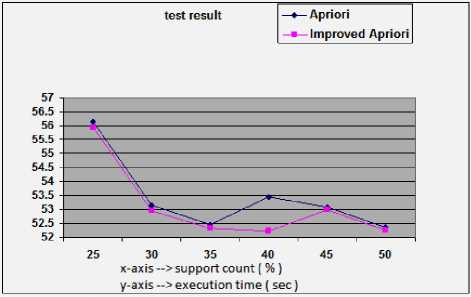
Fig. 8. The comparison of runtime at different minimum supports between the original Apriori and the improved Apriori

Fig. 7 and Fig. 8 show the execution times for the two datasets for increasing values of minimum support. As the minimum support increases, the execution time of the algorithm decreases because of decreases in the total number of candidates and large itemsets. From the above result, we can contrast the changes in efficiency. With the decrease of minimum support to some content, the Improved Apriori algorithm tends to prevail, and with the further decrease of minimum support, the advantage of the Improved Apriori algorithm can be greatly enhanced.

From the above figures, we can conclude that, with the reduction of the minimum support, the efficiency of the Improved Apriori algorithm can change correspondingly from a lower level to a higher level than that of the classic Apriori algorithm. When the value of minimum support count is small enough, the efficiency of the modified algorithm is improved. The total number of records and the characteristic of data will affect the performance of the algorithm.

• VII. Conclusion And Future Work

The proposed algorithm for mining association rule, decreases pruning operations of candidate 2-itemsets, thereby saving time and increase efficiency. It optimizes subset operation, through the transaction tag to speed up support calculations. The experimental results obtained from tests show that proposed system outperforms original one efficiently.

The current mining methods require users to define one or more parameters before their execution; however, most of them do not mention how users can adjust these parameters online while they are running. It is not feasible for users to wait until a mining algorithm to stop before they can reset the parameters. This is because it may take a long time for the algorithm to finish due to the continuous arrival and huge amount of data. For further improvement, we may consider either let the users adjust online or let the mining algorithm auto-adjust most of the key parameters in association rule mining, such as support, confidence and error rate.